Maharashtra Board 11th Commerce Maths Solutions Chapter 1 Partition Values Ex 1.1

Balbharati Maharashtra State Board 11th Commerce Maths Solution Book Pdf Chapter 1 Partition Values Ex 1.1 Questions and Answers.

Maharashtra State Board 11th Commerce Maths Solutions Chapter 1 Partition Values Ex 1.1

Question 1.
Compute all the quartiles for the following series of observations:
16, 14.9, 11.5, 11.8, 11.1, 14.5, 14, 12, 10.9, 10.7, 10.6, 10.5, 13.5, 13, 12.6
Solution:
The given data can be arranged in ascending order as follows:
10.5, 10.6, 10.7, 10.9, 11.1, 11.5, 11.8, 12, 12.6, 13, 13.5, 14, 14.5, 14.9, 16
Here, n = 15
Q₁ = value of \(\left(\frac{n+1}{4}\right)^{\text {th }}\) observation
= value of \(\left(\frac{15+1}{4}\right)^{\text {th }}\) observation
= value of 4th observation
∴ Q₁ = 10.9
Q₂ = value of 2\(\left(\frac{n+1}{4}\right)^{\text {th }}\) observation
= value of 2\(\left(\frac{15+1}{4}\right)^{\text {th }}\) observation
= value of (2 × 4)th observation
= value of 8th observation
∴ Q₂ = 12
Q₃ = value of 3\(\left(\frac{n+1}{4}\right)^{\text {th }}\) observation
= value of 3\(\left(\frac{15+1}{4}\right)^{\text {th }}\) observation
= value of (3 × 4)th observation
= value of 12th observation
∴ Q₃ = 14

Question 2.
The heights (in cm.) of 10 students are given below:
148, 171, 158, 151, 154, 159, 152, 163, 171, 145
Calculate Q₁ and Q₃ for the above data.
Solution:
The given data can be arranged in ascending order as follows:
145, 148, 151, 152, 154, 158, 159, 163, 171, 171
Here, n = 10
Q₁ = value of \(\left(\frac{n+1}{4}\right)^{\text {th }}\) observation
= value of \(\left(\frac{10+1}{4}\right)^{\text {th }}\) observation
= value of (2.75)th observation
= value of 2nd observation + 0.75 (value of 3rd observation – value of 2nd observation)
= 148 + 0.75 (151 – 148)
= 148 + 0.75(3)
= 148 + 2.25
∴ Q₁ = 150.25
Q₃ = value of 3\(\left(\frac{n+1}{4}\right)^{\text {th }}\) observation
= value of 3\(\left(\frac{10+1}{4}\right)^{\text {th }}\) observation
= value of (3 × 2.75)th observation
= value of (8.25)th observation
= value of 8th observation + 0.25 (value of 9th observation – value of 8th observation)
= 163 + 0.25(171 – 163)
= 163 + 0.25(8)
= 163 + 2
∴ Q₃ = 165

Question 3.
The monthly consumption of electricity (in units) of families in a certain locality is given below:
205, 201, 190, 188, 195, 172, 210, 225, 215, 232, 260, 230
Calculate electricity consumption (in units) below which 25% of the families lie.
Solution:
To find the consumption of electricity below which 25% of the families lie, we have to find Q₁.
Monthly consumption of electricity (in units) can be arranged in ascending order as follows:
172, 188, 190, 195, 201, 205, 210, 215, 225, 230, 232, 260.
Here, n = 12
Q₁ = value of \(\left(\frac{n+1}{4}\right)^{\text {th }}\) observation
= value of \(\left(\frac{12+1}{4}\right)^{\text {th }}\) observation
= value of (3.25)th observation
= value of 3rd observation + 0.25 (value of 4th observation – value of 3rd observation)
= 190 + 0.25(195 – 190)
= 190 + 0.25(5)
= 190 + 1.25
= 191.25
∴ the consumption of electricity below which 25% of the families lie is 191.25.

Question 4.
For the following data of daily expenditure of families (in ₹), compute the expenditure below which 75% of families include their expenditure.

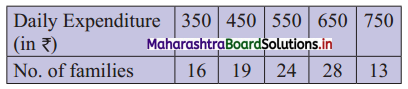
Solution:
To find the expenditure below which 75% of families have their expenditure, we have to find Q₃.
We construct the less than cumulative frequency table as given below:

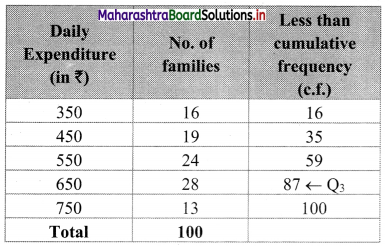
Here, n = 100
Q₃ = value of 3\(\left(\frac{n+1}{4}\right)^{\text {th }}\) observation
= value of 3\(\left(\frac{100+1}{4}\right)^{\text {th }}\) observation
= value of (3 × 25.25)th observation
= value of (75.75)th observation
Cumulative frequency which is just greater than (or equal to) 75.75 is 87.
∴ Q₃ = 650
∴ the expenditure below which 75% of families include their expenditure is ₹ 650.

Question 5.
Calculate all the quartiles for the following frequency distribution:

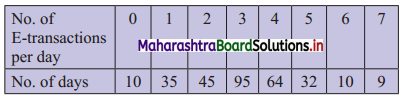
Solution:
We construct the less than cumulative frequency table as given below:

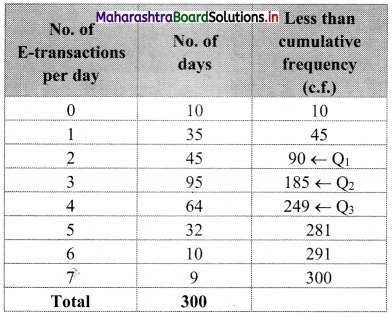
Here, n = 300
Q₁ = value of \(\left(\frac{n+1}{4}\right)^{\text {th }}\) observation
= value of \(\left(\frac{300+1}{4}\right)^{\text {th }}\) observation
= value of (75.25)th observation
Cumulative frequency which is just greater than (or equal to) 75.25 is 90.
∴ Q₁ = 2
Q₂ = value of 2\(\left(\frac{n+1}{4}\right)^{\text {th }}\) observation
= value of 2\(\left(\frac{300+1}{4}\right)^{\text {th }}\) observation
= value of (2 × 75.25)th observation
= value of (150.50)th observation
∴ Cumulative frequency which is just greater than (or equal to) 150.50 is 185.
∴ Q₂ = 3
Q₃ = value of 3\(\left(\frac{n+1}{4}\right)^{\text {th }}\) observation
= value of 3\(\left(\frac{300+1}{4}\right)^{\text {th }}\) observation
= value of (3 × 75.25)th observation
= value of (225.75)th observation
Cumulative frequency which is just greater than (or equal to) 225.75 is 249.
∴ Q₃ = 4

Question 6.
The following is the frequency distribution of heights of 200 male adults in a factory:

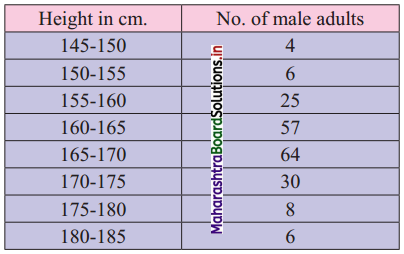
Find the central height.
Solution:
To find the central height, we have to find Q₂.
We construct the less than cumulative frequency table as given below:

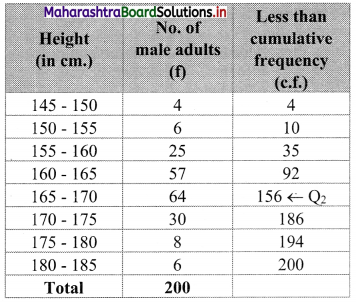
Here, N = 200
Q₂ class = class containing \(\left(\frac{2 \mathrm{~N}}{4}\right)^{\mathrm{th}}\) observation
∴ \(\frac{2 \mathrm{~N}}{4}=\frac{2 \times 200}{4}\) = 100
Cumulative frequency which is just greater than (or equal to) 100 is 156.
∴ Q₂ lies in the class 165 – 170.
∴ L = 165, h = 5, f = 64, c.f. = 92
Q₂ = \(\mathrm{L}+\frac{\mathrm{h}}{\mathrm{f}}\left(\frac{2 \mathrm{~N}}{4}-\text { c.f. }\right)\)
= 165 + \(\frac{5}{64}\) (100 – 92)
= 165 + \(\frac{5}{64}\) × 8
= 165 + \(\frac{5}{8}\)
= 165 + 0.625
= 165.625
∴ Central height is 165.625 cm.

Question 7.
The following is the data of pocket expenditure per week of 50 students in a class. It is known that the median of the distribution is ₹ 120. Find the missing frequencies.

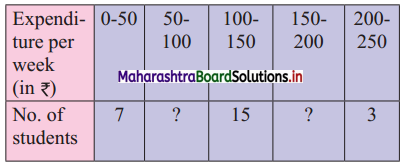
Solution:
Let a and b be the missing frequencies of class 50 – 100 and class 150 – 200 respectively.
We construct the less than cumulative frequency table as given below:

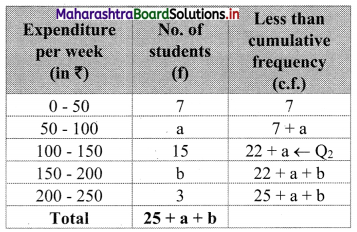
Here, N = 25 + a + b
Since, N = 50
∴ 25 + a + b = 50
∴ a + b = 25 …..(i)
Given, Median = Q₂ = 120
∴ Q2 lies in the class 100 – 150.
∴ L = 100, h = 50, f = 15, \(\frac{2 \mathrm{~N}}{4}=\frac{2 \times 50}{4}\) = 25
∴ Q₂ = \(\mathrm{L}+\frac{\mathrm{h}}{\mathrm{f}}\left(\frac{2 \mathrm{~N}}{4}-\text { c.f. }\right)\)
∴ 120 = 100 + \(\frac{50}{15}\) [25 – (7 + a)]
∴ 120 – 100 = \(\frac{10}{3}\) (25 – 7 – a)
∴ 20 = \(\frac{10}{3}\) (18 – a)
∴ \(\frac{60}{10}\) = 18 – a
∴ 6 = 18 – a
∴ a = 18 – 6 = 12
Substituting the value of a in equation (i), we get
12 + b = 25
∴ b = 25 – 12 = 13
∴ 12 and 13 are the missing frequencies of the class 50 – 100 and class 150 – 200 respectively.

Question 8.
The following is the distribution of 160 workers according to the wages in a certain factory:

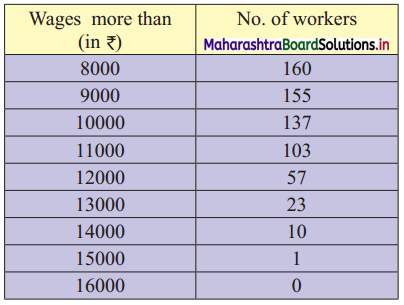
Determine the values of all quartiles and interpret the results.
Solution:
The given table is a more than cumulative frequency.
We transform the given table into less than cumulative frequency.
We construct the less than cumulative frequency table as given below:

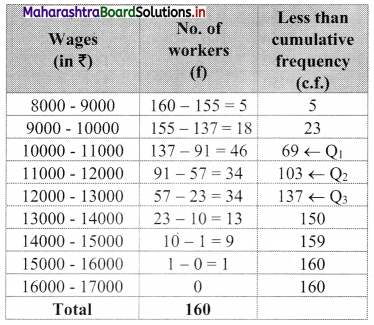
Here, N = 160
∴ Q₁ class = class containing \(\left(\frac{\mathrm{N}}{4}\right)^{\text {th }}\) observation
∴ \(\frac{\mathrm{N}}{4}=\frac{160}{4}\) = 40
Cumulative frequency which is just greater than (or equal to) 40 is 69.
∴ Q₁ lies in the class 10000 – 11000
∴ L = 10000, h = 1000, f = 46, c.f. = 23
Q₁ = \(L+\frac{h}{f}\left(\frac{N}{4}-\text { c.f. }\right)\)
= 10000 + \(\frac{1000}{46}\) (40 – 23)
= 10000 + \(\frac{1000}{46}\) (17)
= 10000 + \(\frac{17000}{46}\)
= 10000 + 369.57
= 10369.57
Q₂ class = class containing \(\left(\frac{2 \mathrm{~N}}{4}\right)^{\mathrm{th}}\) observation
∴ \(\frac{2 \mathrm{~N}}{4}=\frac{2 \times 160}{4}\) = 80
Cumulative frequency which is just greater than (or equal to) 80 is 103.
∴ Q₂ lies in the class 11000 – 12000.
∴ L = 11000, h = 1000, f = 34, c.f. = 69
∴ Q₂ = \(L+\frac{h}{f}\left(\frac{2 N}{4}-\text { c.f. }\right)\)
= 11000 + \(\frac{1000}{34}\)(80 – 69)
= 11000 + \(\frac{1000}{34}\)(11)
= 11000 + \(\frac{11000}{34}\)
= 11000 + 323.529
= 11323.529
Q₃ class = class containing \(\left(\frac{3 \mathrm{~N}}{4}\right)^{\text {th }}\) observation
∴ \(\frac{3 \mathrm{~N}}{4}=\frac{3 \times 160}{4}\) = 120
Cumulative frequency which is just greater than (or equal to) 120 is 137.
∴ Q₃ lies in the class 12000 – 13000.
∴ L = 12000, h = 1000, f = 34, c.f. = 103
∴ Q₃ = \(\frac{h}{f}\left(\frac{3 N}{4}-c . f .\right)\)
= 12000 + \(\frac{1000}{34}\) (120 – 103)
= 12000 + \(\frac{1000}{34}\) (17)
= 12000 + \(\frac{1000}{2}\)
= 12000 + 500
= 12500
Interpretation:
Q₁ < Q₂ < Q₃

Question 9.
Following is grouped data for the duration of fixed deposits of 100 senior citizens from a certain bank:

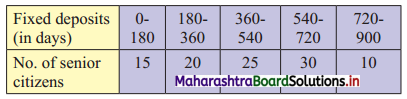
Calculate the limits of fixed deposits of central 50% senior citizens.
Solution:
We construct the less than cumulative frequency table as given below:

To find the limits of fixed deposits of central 50% senior citizens, we have to find Q₁ and Q₃.
Here, N = 100
Q₁ class = class containing \(\left(\frac{\mathrm{N}}{4}\right)^{\text {th }}\) observation
∴ \(\frac{N}{4}=\frac{100}{4}\) = 25
Cumulative frequency which is just greater than (or equal to) 25 is 35.
∴ Q1 lies in the class 180 – 360.
∴ L = 180, h = 180, f = 20, c.f. = 15
∴ Q₁ = \(L+\frac{h}{f}\left(\frac{N}{4}-c . f .\right)\)
= 180 + \(\frac{180}{20}\) (25 – 15)
= 180 + 9(10)
= 180 + 90
∴ Q₁ = 270
Q₃ class = class containing \(\left(\frac{3 \mathrm{N}}{4}\right)^{\text {th }}\) observation
∴ \(\frac{3 \mathrm{N}}{4}=\frac{3 \times 100}{4}\) = 75
Cumulative frequency which is just greater than (or equal to) 75 is 90.
∴ Q₃ lies in the class 540 – 720.
∴ L = 540, h = 180, f = 30, c.f. = 60
∴ Q₃ = \(L+\frac{h}{f}\left(\frac{3 N}{4}-c . f .\right)\)
= 540 + \(\frac{180}{30}\) (75 – 60)
= 540 + 6(15)
= 540 + 90
∴ Q₃ = 630
∴ Limits of duration of fixed deposits of central 50% senior citizens is from 270 to 630.

Question 10.
Find the missing frequency given that the median of the distribution is 1504.

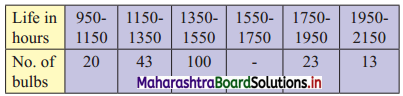
Solution:
Let x be the missing frequency of the class 1550 – 1750.
We construct the less than frequency table as given below:

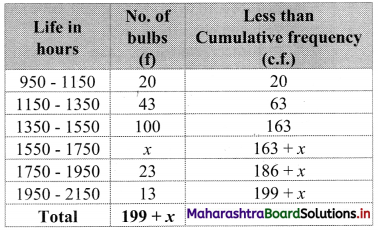
Here, N = 199 + x
Given, Median (Q₂) = 1504
∴ Q₂ lies in the class 1350 – 1550.
∴ L = 1350, h = 200, f = 100, c.f. = 63,
\(\frac{2 \mathrm{~N}}{4}=\frac{199+x}{2}\)
∴ Q₂ = \(L+\frac{h}{f}\left(\frac{2 N}{4}-c . f .\right)\)
∴ 1504 = 1350 + \(\frac{200}{100}\left(\frac{199+x}{2}-63\right)\)
∴ 1504 – 1350 = 2\(\left(\frac{199+x-126}{2}\right)\)
∴ 154 = 199 + x – 126
∴ 154 = x + 73
∴ x = 81