Balbharti Maharashtra State Board Class 9 Maths Solutions covers the Practice Set 9.3 Geometry 9th Class Maths Part 2 Answers Solutions Chapter 9 Surface Area and Volume.
Practice Set 9.3 Geometry 9th Std Maths Part 2 Answers Chapter 9 Surface Area and Volume
Question 1.
Find the surface areas and volumes of spheres of the following radii
i. 4 cm
ii. 9 cm
iii. 3.5 cm (π = 3.14)
i. Given: Radius (r) = 4 cm
To find: Surface area and volume of sphere
Solution:
Surface area of sphere = 4πr2
= 4 x 3.14 x 42
∴ Surface area of sphere = 200.96 sq.cm
Volume of sphere = \(\frac { 4 }{ 3 }\)πr3
= \(\frac { 4 }{ 3 }\) x 3.14 x 42
∴ Volume of sphere = 267.95 cubic cm
ii. Given: Radius (r) = 9 cm
To find: Surface area and volume of sphere
Solution:
Surface area of sphere = 4πr2
= 4 x 3.14 x 92
∴ Surface area of sphere = 1017.36 sq.cm
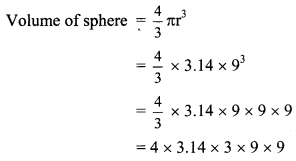
∴ Volume of sphere = 3052.08 cubic cm
iii. Given: Radius (r) = 3.5 cm
To find: Surface area and volume of sphere
Solution:
Surface area of sphere = 4πr2
= 4 x 3.14 x (3.5)2
∴ Surface area of sphere = 153.86 sq.cm
Volume of sphere = \(\frac { 4 }{ 3 }\) πr3
= \(\frac { 4 }{ 3 }\) x 3.14 x (3.5)3
∴ Volume of sphere = 179.50 cubic cm
Question 2.
If the radius of a solid hemisphere is 5 cm, then find its curved surface area and total surface area, (π = 3.14)
Given: Radius (r) = 5 cm
To find: Curved surface area and total surface area of hemisphere
Solution:
i. Curved surface area of hemisphere = 2πr2
= 2 x 3.14 x 52
= 2 x 3.14 x 25
= 50 x 3.14
= 157 sq.cm.
ii. Total surface area of hemisphere = 3πr2
= 3 x 3.14 x 52
= 235.5 sq.cm.
∴ The curved surface area and totai surface area of hemisphere are 157 sq.cm, and 235.5 sq.cm, respectively.
Question 3.
If the surface area of a sphere is 2826 cm2 then find its volume. (π = 3.14)
Given: Surface area of sphere = 2826 sq.cm.
To find: Volume of sphere
Solution:
i. Surface area of sphere = 4πr2
∴ 2826 = 4 x 3.14 x r2
2826 = 282600 = 900
∴ \( r^{2}=\frac{2826}{4 \times 3.14}=\frac{282600}{4 \times 314}=\frac{900}{4}\)
∴ r2 = 225
∴ r = \(\sqrt { 225 }\) … [Taking square root on both sides]
= 15 cm
ii. Volume of sphere = \(\frac { 4 }{ 3 }\) πr3
= \(\frac { 4 }{ 3 }\) x 3.14 x 153
= \(\frac { 4 }{ 3 }\) x 3.14 x 15 x 15 x 15
= 4 x 3.14 x 5 x 15 x 15
= 14130 cubic cm.
∴ The volume of the sphere is 14130 cubic cm.
Question 4.
Find the surface area of a sphere, if its volume is 38808 cubic cm. (π = \(\frac { 22 }{ 7 }\))
Given: Volume of sphere = 38808 cubic cm.
To find: Surface area of sphere
Solution:
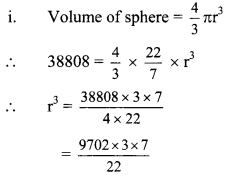
∴ r3 = 441 x 21 = 21 x 21 x 21
∴ r = 21 cm … [Taking cube root on both sides]
ii. Surface area of sphere = 4πr2
= 4 x \(\frac { 22 }{ 7 }\) x 21
= 4 x \(\frac { 22 }{ 7 }\) x 21 x 21
= 4 x 22 x 3 x 21
= 5544 sq.cm.
∴ The surface area of sphere is 5544 sq.cm.
Question 5.
Volume of a hemisphere is 18000π cubic cm. Find its diameter.
Given: Volume of hemisphere = 1 8000π cubic cm.
To find: Diameter of the hemisphere
Solution:
i. Volume of hemisphere = \(\frac { 2 }{ 3 }\) πr3
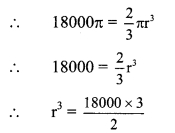
= 9000 x 3
∴ r3 = 27000
∴ r = \(\sqrt [ 3 ]{ 27000 }\) … [Taking cube root on both sides]
= 30 cm
ii. Diameter = 2r
= 2 x 30 = 60 cm
∴ The diameter of the hemisphere is 60 cm.