Balbharti Maharashtra State Board Class 9 Maths Solutions covers the Practice Set 7.2 Geometry 9th Class Maths Part 2 Answers Solutions Chapter 7 Co-ordinate Geometry.
Practice Set 7.2 Geometry 9th Std Maths Part 2 Answers Chapter 7 Co-ordinate Geometry
Question 1.
On a graph paper plot the points A(3, 0), B(3, 3), C(0, 3). Join A, B and B, C. What is the figure formed?
Soiution:
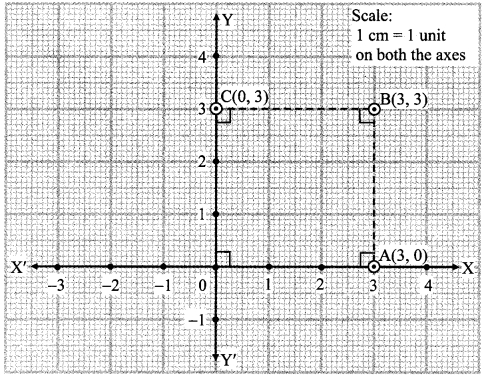
d(O, A) = 3 cm, d(A, B) = 3 cm, d(B, C) = 3 cm, d(O, C) = 3 cm and each angle of □ OABC is 90°
∴ □ OABC is a square.
Question 2.
Write the equation of the line parallel to the Y-axis at a distance of 7 units from it to its left.
Solution:
The equation of a line parallel to the Y-axis is x = a.
Since, the line is at a distance of 7 units to the left of Y-axis,
∴ a = -7
∴ x = -1 is the equation of the required line.
Question 3.
Write the equation of the line parallel to the X-axis at a distance of 5 units from it and below the X-axis.
Solution:
The equation of a line parallel to the X-axis is y = b.
Since, the line is at a distance of 5 units below the X-axis.
∴ b = -5
∴ y = -5 is the equation of the required line.
Question 4.
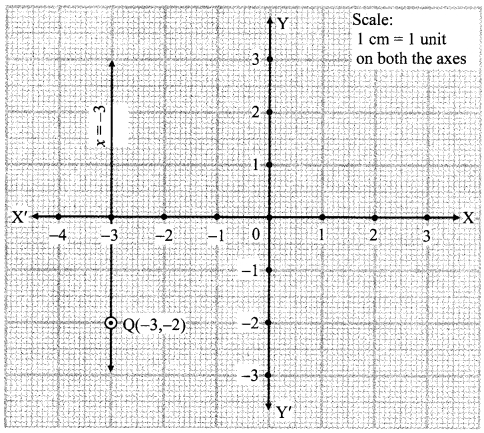
The point Q( -3, -2) lies on a line parallel to the Y-axis. Write the equation of the line and draw its graph.
Solution:
The equation of a line parallel to the Y-axis is x = a.
Here, a = -3
∴ x = -3 is the equation of the required line.
Question 5.
Y-axis and line x = – 4 are parallel lines. What is the distance between them?
Solution:
Equation of Y-axis is x = 0.
Equation of the line parallel to the Y-axis is x = – 4. … [Given]
∴ Distance between the Y-axis and the line x = – 4 is 0 – (- 4) … [0 > -4]
= 0 + 4 = 4 units
∴ The distance between the Y-axis and the line x = – 4 is 4 units.
[Note: The question is modified as X-axis cannot be parallel to the line x = – 4.]
Question 6.
Which of the equations given below have graphs parallel to the X-axis, and which ones have graphs parallel to the Y-axis? [1 Mark each]
i. x = 3
ii. y – 2 = 0
iii. x + 6 = 0
iv. y = -5
Solution:
i. The equation of a line parallel to the Y-axis is x = a.
∴ The line x = 3 is parallel to the Y-axis.
ii. y – 2 = 0
∴ y = 2
The equation of a line parallel to the X-axis is y = b.
∴ The line y – 2 = 0 is parallel to the X-axis.
iii. x + 6 = 0
∴ x = -6
The equation of a line parallel to the Y-axis is x = a.
∴ The line x + 6 = 0 is parallel to the Y-axis.
iv. The equation of a line parallel to the X-axis is y = b.
∴ The line y = – 5 is parallel to the X-axis.
Question 7.
On a graph paper, plot the points A(2, 3), B(6, -1) and C(0, 5). If these points are collinear, then draw the line which includes them. Write the co-ordinates of the points at which the line intersects the X-axis and the Y-axis.
Solution:
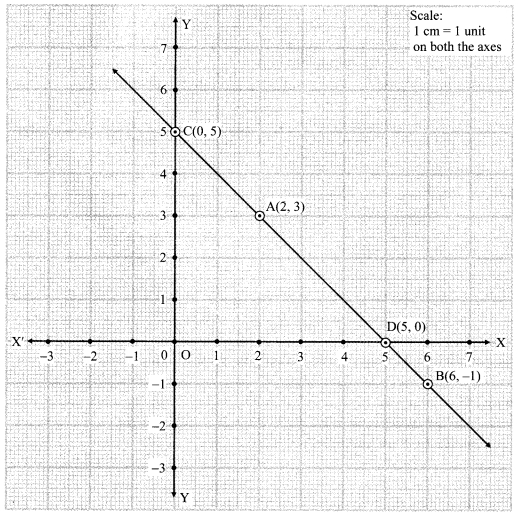
From the graph, the line drawn intersects the X-axis at D(5, 0) and the Y-axis at C(0, 5).
Question 8.
Draw the graphs of the following equations on the same system of co-ordinates. Write the co-ordinates of their points of intersection.
x + 4 = 0,
y – 1 = 0,
2x + 3 = 0,
3y – 15 = 0
Solution:
i. x + 4 = 0
∴ x = – 4
ii. y – 1 = 0
∴ y = 1
iii. 2x + 3 = 0
∴2x = -3
∴ x = \(\frac { -3 }{ 2 }\)
∴ x = -1.5
iv. 3y- 15 = 0
3y = 15
y = \(\frac { 15 }{ 3 }\)
∴ y = 5
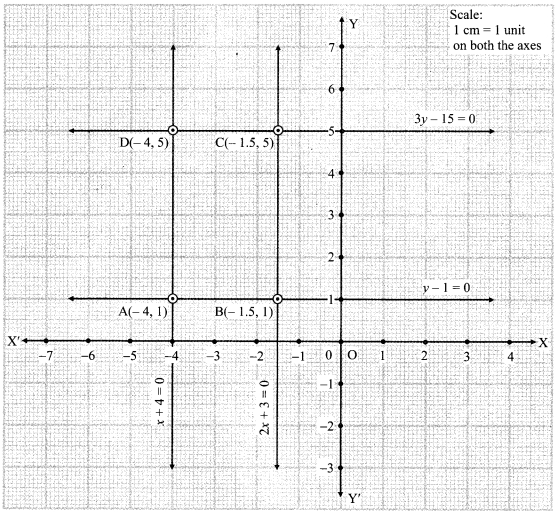
The co-ordinates of the point of intersection of x + 4 = 0 and y – 1 = 0 are A(-4, 1).
The co-ordinates of the point of intersection ofy – 1 = 0 and 2x + 3 = 0 are B(-1.5, 1).
The co-ordinates of the point of intersection of 3y – 15 = 0 and 2x + 3 = 0 are C(-1.5, 5).
The co-ordinates of the point of intersection of x + 4 = 0 and 3y – 15 = 0 are D(-4, 5).
Question 9.
Draw the graphs of the equations given below.
i. x + y = 2
ii. 3x – y = 0
iii. 2x + y = 1
Solution:
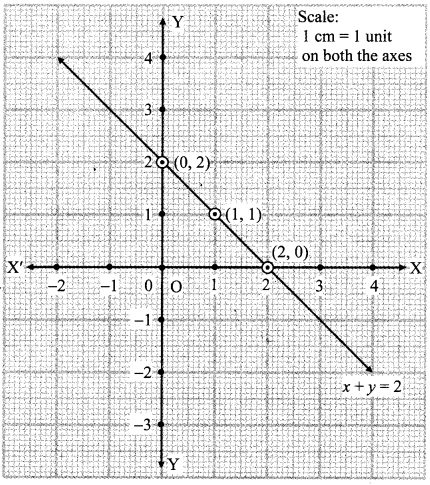
i. x + y = 2
∴ y = 2 – x
When x = 0,
y = 2 – x
= 2 – 0
= 2
When x = 1,
y = 2 – x
= 2 – 1
= 1
When x = 2,
y = 2 – x
= 0

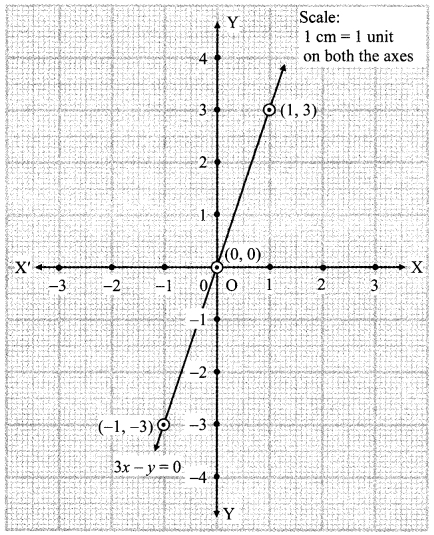
ii. 3x – y = 0
∴ y = 3x
When x = 0,
y = 3x
= 3(0)
= 0
When x = 1,
y = 3x
= 3(1)
= 3
When x = -1,
y = 3x
= 3(-1)
= -3

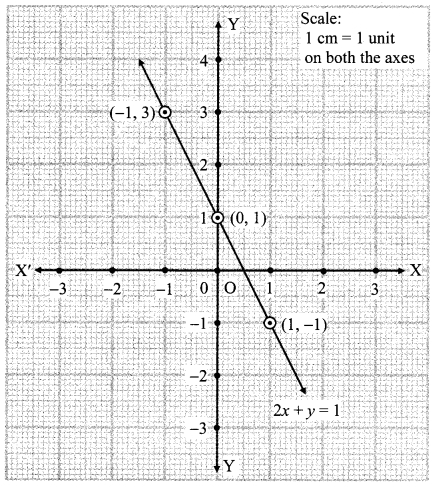
iii. 2x + y = 1
∴ y = 1 – 2x
When x = 0,
y = 1 – 2x
= 1 – 2(0)
= 1 – o
When x = 1,
y = 1 – 2x
= 1- 2(1)
= 1 – 2
= -1
When x = -1,
y = 1 – 2x
= 1 – 2(-1)
= 1 + 2
= 3
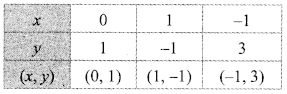
Maharashtra Board Class 9 Maths Chapter 7 Co-ordinate Geometry Practice Set 7.2 Intext Questions and Activities
Question 1.
i. Can we draw a line parallel to the X-axis at a distance of 6 unIts from It and below the X-axis?
ii. Will all of the points (-3,-6), (10,-6), ( \(\frac { 1 }{ 2 }\), -6) be on that line?
iii. What would be the equation of this line?(Textbook pg. no. 94)
Solution:
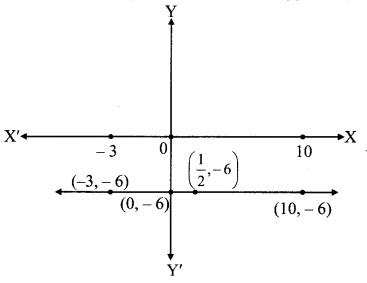
i. Yes.
This line will pass through the point (0,-6).
ii. Yes.
Here, y co-ordinate of the points (-3, -6), (10,-6), ( \(\frac { 1 }{ 2 }\), -6) is the same, which is -6.
∴ All the above points lie on the same line.
iii. Since, the line is at a distance of 6 units below the X-axis.
∴ b = -6
∴ Equation of the line is y = -6.
Question 2.
i. Can we draw a line parallel to the Y – axis at a distance of 2 units from ¡t and to its right?
ii. Will all of the points (2, 10), (2, 8), (2, -) be on that line?
iii. What would be the equation of this line? (Textbook pg. no. 95)
Solution:
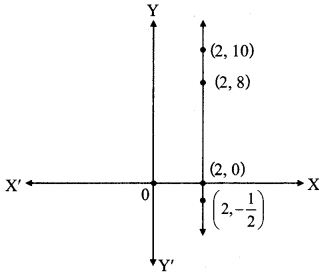
i. Yes.
(2, 10)
This line will pass through the point (2, 0).
(2,8)
ii. Yes.
Here, x co-ordinate of the points (2, 10), (2, 8), (2,-\(\frac { 1 }{ 2 }\) ) is the same, which is 2.
∴ All the above points lie on the same line.
iii. Since, the line is at a distance of 2 units to the right of Y-axis.
a = 2
∴ Equation of the line is x = 2.
Question 3.
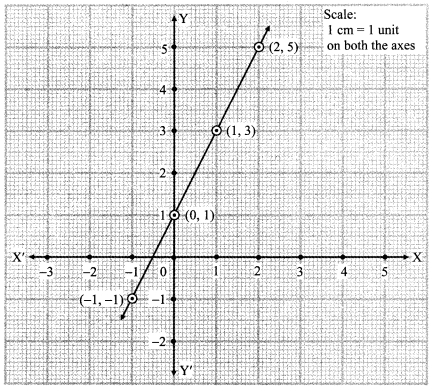
On a graph paper, plot the points (0, 1), (1, 3), (2, 5). Are they collinear? If so, draw the line that passes through them.
i. Through which quadrants does this line pass ?
ii. Write the co-ordinates of the point at which it intersects the Y-axis.
iii. Show any point in the third quadrant which lies on this line. Write the co-ordinates of the point. (Textbook pg. no. 96)
Solution:
i. The line passes through the quadrants I, II and III.
ii. The line intersects the Y-axis at (0, 1).
iii. (-1,-1)