Balbharti Maharashtra State Board Class 9 Maths Solutions covers the Practice Set 2.2 Geometry 9th Class Maths Part 2 Answers Solutions Chapter 2 Parallel Lines.
Practice Set 2.2 Geometry 9th Std Maths Part 2 Answers Chapter 2 Parallel Lines
Question 1.
In the given figure, y = 108° and x = 71°. Are the lines m and n parallel? Justify?
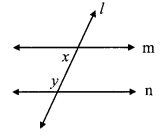
Solution:
y = 108°, x = 71° …[Given]
x + y = 71° + 108°
= 179°
∴ x + y = 180°
∴ The angles x andy are not supplementary.
∴ The angles do not satisfy the interior angles test for parallel lines
∴ line m and line n are not parallel lines.
Question 2.
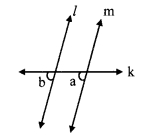
In the given figure, if ∠a = ∠b then prove that line l || line m.
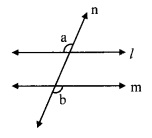
Given: ∠a ≅ ∠b
To prove: line l| line m
Solution:
Proof:
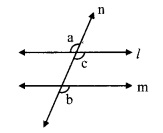
consider ∠c as shown in the figure ∠a ≅ ∠c …….. (i) [Vertically opposite angles]
But, ∠a ≅ ∠b I (ii) [Given]
∴ ∠b ≅ ∠c [From (i) and (ii)]
But, ∠b and ∠c are corresponding angles on lines l and m when line n is the transversal.
∴ line l || line m. [Corresponding angles test]
Question 3.
In the given figure, if ∠a ≅ ∠b and ∠x ≅ ∠y, then prove that line l | line n.
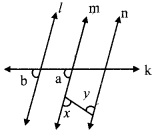
Given: ∠a ≅ ∠b and ∠x ≅ ∠y
To prove: line l | line n
Solution:
Proof:
∠a = ∠b [Given]
But, ∠a and ∠b are corresponding angles on lines l and m when line k is the transversal.
∴ line l || line m ….(i) [Corresponding angles test]
∠x ≅ ∠y [Given]
But, ∠x and ∠y are alternate angles on lines m and n when seg PQ is the transversal,
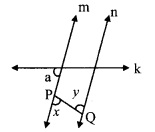
∴ line m || line n ……(ii) [Alternate angles test]
∴ From (i) and (ii),
line l || line m || line n
i.e., line l || line n
Question 4.
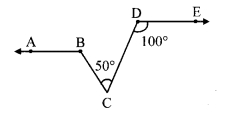
In the given figure, if ray BA || ray DE, ∠C = 50° and ∠D = 100°. Find the measure of ∠ABC.
(Hint: Draw a line passing through point C and parallel to line AB.)
Solution:
Draw a line FG passing through point
C and parallel to line AB
line FG || ray BA …….(i) [Construction]
Ray BA || ray DE ….(ii) [Given]
line FG || ray BA || ray DE …(iii) [From (i) and (ii)]
line FG||rayDE [From (iii)]
and seg DC is their transvensal
∴ ∠ DCF = ∠ EDC [Alternate angles]
∴ ∠ DCF = 100° [∵ ∠D = 100°]
Now, ∠ DCF = ∠ BCF + ∠ BCD [Angle addition property]
∴ 100° = ∠BCF + 50°
∴ 100° – 50° = ∠BCF
∴ ∠BCF = 50° ….(iv)
Now, line FG || ray BA and seg BC is their transversal.
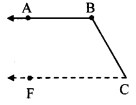
∴ ∠ABC + ∠BCF = 180° [Interior angles]
∴ ∠ABC + 50° = 180° [From (iv)]
∴ ∠ABC = 180°- 50°
∴ ∠ABC = 130°
Question 5.
In the given figure, ray AE || ray BD, ray AF is the bisector of ∠EAB and ray BC is the bisector of ∠ABD. Prove that line AF || line BC.
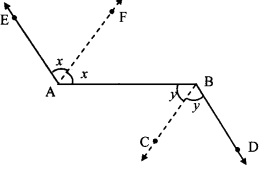
Given: Ray AE || ray BD, and
ray AF and ray BC are the bisectors of ∠EAB and ∠ABD respectively.
To prove: line AF || line BC
Solution:
Proof:
Ray AE || ray BD and seg AB is their transversal.
∴ ∠EAB = ∠ABD ….(i) [Alternate angles]
∠FAB = \(\frac { 1 }{ 2 }\)∠EAB [Ray AF bisects ∠EAB]
∴ 2∠FAB = ∠EAB …..(ii)
∠CBA = \(\frac { 1 }{ 2 }\)∠ABD [Ray BC bisects ∠ABD]
∴ 2∠CBA = ∠ABD …(iii)
∴ 2∠FAB = 2∠CBA [From (i), (ii) and (iii)]
∴ ∠FAB = ∠CBA
But, ∠FAB and ∠ABC are alternate angles on lines AF and BC when seg AB is the transversal.
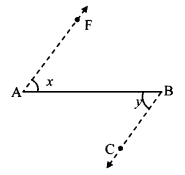
∴ line AF || line BC [Alternate angles test]
Question 6.
A transversal EF of line AB and line CD intersects the lines at points P and Q respectively. Ray PR and ray QS are parallel and bisectors of ∠BPQ and ∠PQC respectively. Prove that line AB || line CD.
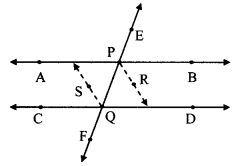
Given: Ray PR || ray QS
Ray PR and ray QS are the bisectors of ∠BPQ and ∠PQC respectively.
To prove: line AB || line CD
Solution:
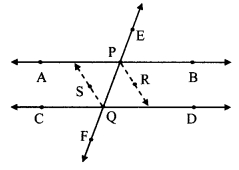
Proof:
Ray PR || ray QS and seg PQ is their transversal.
∠RPQ = ∠SQP ….(i) [Alternate angles]
∠RPQ = \(\frac { 1 }{ 2 }\)∠BPQ …. (ii) [Ray PR bisects ∠BPQ]
∠SQP = \(\frac { 1 }{ 2 }\)∠PQC [Ray QS bisects ∠PQC]
∴ \(\frac { 1 }{ 2 }\)∠BPQ = \(\frac { 1 }{ 2 }\)∠PQC
∴ ∠BPQ = ∠PQC
But, ∠BPQ and ∠PQC are alternate angles on lines AB and CD when line EF is the transversal.
∴ line AB || line CD [Alternate angles test]
Maharashtra Board Class 9 Maths Chapter 2 Parallel Lines Practice Set 2.2 Intext Questions and Activities
Question 1.
In the given figure, how will you decide whether line ¡ and line m are parallel or not? (Textbook pg. no. 19)

Answer:
In the figure, we observe that line I and line m are coplanar and do not intersect each other.
∴ Line l and line m are parallel lines.