Balbharti Maharashtra State Board Class 9 Maths Solutions covers the Practice Set 1.1 Geometry 9th Class Maths Part 2 Answers Solutions Chapter 1 Basic Concepts in Geometry.
Practice Set 1.1 Geometry 9th Std Maths Part 2 Answers Chapter 1 Basic Concepts in Geometry
Question 1.
Find the distances with the help of the number line given below.

i. d(B, E)
ii. d (J, J)
iii. d(P, C)
iv. d(J, H)
v. d(K, O)
vi. d(O, E)
vii. d(P, J)
viii. d(Q, B)
Solution:
i. Co-ordinate of the point B is 2.
Co-ordinate of the point E is 5.
Since, 5 > 2
∴ d(B, E) = 5 – 2
∴ d(B, E) = 3
ii. Co-ordinate of the point J is -2.
Co-ordinate of the point A is 1.
Since, 1 > -2
∴ d(J, A) = 1 – (-2)
= 1 + 2
∴ d(J, A) = 3
iii. Co-ordinate of the point P is -4.
Co-ordinate of the point C is 3.
Since, 3 > -4
∴ d(P,C) = 3 – (-4)
= 3 + 4
∴ d(P,C) = 7
iv. Co-ordinate of the point J is -2.
Co-ordinate of the point H is -1.
Since, -1 > -2
∴ d(J,H) = – 1 – (-2)
= -1 + 2
∴ d(J,H) = 1
v. Co-ordinate of the point K is -3.
Co-ordinate of the point O is 0.
Since,0 > -3
∴ d(K, O) = 0 – (-3)
= 0 + 3
∴ d(K, O) = 3
vi. Co-ordinate of the point O is 0.
∴ Co-ordinate of the point E is 5.
Since, 5 > 0
∴ d(O, E) = 5 – 0
∴ d(O, E) = 5
vii. Co-ordinate of the point P is -4.
Co-ordinate of the point J is -2.
Since -2 > -4
∴ d(P, J) = -2 – (-4)
= – 2+ 4
∴ d(P, J) = 2
viii. Co-ordinate of the point Q is -5.
Co-ordinate of the point B is 2.
Since,2 > -5
∴ d(Q,B) = 2 – (-5)
= 2 + 5
∴ d(Q, B) = 7
Question 2.
If the co-ordinate of A is x and that of B is . y, find d(A, B).
i. x = 1, y = 7
ii. x = 6, y = -2
iii. x = -3, y = 7
iv. x = -4, y = -5
v. x = -3, y = -6
vi. x = 4, y = -8
Solution:
i. Co-ordinate of point A is x = 1.
Co-ordinate of point B is y = 7
Since, 7 > 1
∴ d(A, B) = 7 – 1
∴ d(A, B) = 6
ii. Co-ordinate of point A is x = 6.
Co-ordinate of point B is y = -2.
Since, 6 > -2
∴ d(A, B) = 6 – ( -2) = 6 + 2
∴ d(A, B) = 8
iii. Co-ordinate of point A is x = -3.
Co-ordinate of point B is y = 7.
Since, 7 > -3
∴ d(A, B) = 7 – (-3) = 7 + 3
∴ d(A, B) = 10
iv. Co-ordinate of point A is x = -4.
Co-ordinate of point B is y = -5.
Since, -4 > -5
∴ d(A, B) = -4 – (-5)
= -4 + 5
∴ d(A, B) = 1
v. Co-ordinate of point A is x =-3.
Co-ordinate of point B is y = -6.
Since, -3 > -6
∴ d(A, B) = -3 – (-6)
= -3 + 6
∴ d(A, B) = 3
vi. Co-ordinate of point A is x = 4.
Co-ordinate of point B is y = -8.
Since, 4 > -8
∴ d(A, B) = 4 – (-8)
= 4 + 8
∴d(A, B) = 12
Question 3.
From the information given below, find which of the point is between the other two. If the points are not collinear, state so.
i. d(P, R) = 7, d(P, Q) = 10, d(Q, R) = 3
ii. d(R, S) = 8, d(S, T) = 6, d(R, T) = 4
iii. d(A, B) = 16, d(C, A) = 9, d(B, C) = 7
iv. d(L, M) =11, d(M, N) = 12, d(N, L) = 8
v. d(X, Y) = 15, d(Y, Z) = 7, d(X, Z) = 8
vi. d(D, E) = 5, d(E, F) = 8, d(D, F) = 6
Solution:
i. Given, d(P, R) = 7, d(P, Q) = 10, d(Q, R) = 3
d(P, Q) = 10 …(i)
d(P, R) + d(Q, R) = 7 + 3 = 10 .. .(ii)
∴ d(P, Q) = d(P, R) + d(Q, R) …[From (i) and (ii)]
∴ Point R is between the points P and Q
i. e., P – R – Q or Q – R – P.
∴ Points P, R, Q are collinear.
ii. Given, d(R, S) = 8, d(S, T) = 6, d(R, T) = 4
d(R, S) = 8 …(i)
d(S, T) + d(R, T) = 6 + 4 = 10 …(h)
∴ d(R, S) ≠ d(S, T) + d(R, T) … [From (i) and (ii)]
∴ The given points are not collinear.
iii. Given, d(A, B) = 16, d(C, A) = 9, d(B, C) = 7
d(A, B) = 16 …(i)
d(C, A) + d(B, C) = 9 + 7 = 16 …(ii)
∴ d(A, B) = d(C, A) + d(B, C) …[From(i) and (ii)]
∴ Point C is between the points A and B.
i. e., A – C – B or B – C – A.
∴ Points A, C, B are collinear
iv. Given, d(L, M) = 11, d(M, N) = 12, d(N, L) = 8
d(M, N) = 12 …(i)
d(L, M) + d(N, L) = 11 + 8 = 19 …(ii)
∴d(M, N) + d(L, M) + d(N, L) … [From (i) and (ii)]
∴ The given points are not collinear.
v. Given, d(X, Y) = 15, d(Y, Z) = 7, d(X, Z) = 8
d(X, Y) = 15 …(i)
d(X,Z) + d(Y, Z) = 8 + 7= 15 …(ii)
∴ d(X, Y) = d(X, Z) + d(Y, Z) …[From (i) and (ii)]
∴ Point Z is between the points X and Y
i. e.,X – Z – Y or Y – Z – X.
∴ Points X, Z, Y are collinear.
vi. Given, d(D, E) = 5, d(E, F) = 8, d(D, F) = 6
d(E, F) = 8 …(i)
d(D, E) + d(D, F) = 5 + 6 = 11 …(ii)
∴ d(E, F) ≠ d(D, E) + d(D, F) … [From (i) and (ii)]
∴ The given points are not collinear.
Question 4.
On a number line, points A, B and C are such that d(A, C) = 10, d(C, B) = 8. Find d(A, B) considering all possibilities.
Solution:
Given, d(A, C) = 10, d(C, B) = 8.
Case I: Points A, B, C are such that, A – B – C.
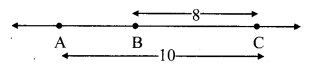
∴ d(A, C) = d(A, B) + d(B, C)
∴ 10 = d(A, B) + 8
∴ d(A, B) = 10 – 8
∴ d(A, B) = 2
Case II: Points A, B, C are such that, A – C – B.
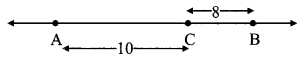
∴ d(A, B) = d(A, C) + d(C, B)
= 10 + 8
∴ d(A, B) = 18
Case III: Points A, B, C are such that, B – A – C.

From the diagram,
d (A, C) > d(B, C)
Which is not possible
∴ Point A is not between B and C.
∴ d(A, B) = 2 or d(A, B) = 18.
Question 5.
Points X, Y, Z are collinear such that d(X, Y) = 17, d(Y, Z) = 8, find d(X, Z).
Solution:
Given,d(X, Y) = 17, d(Y, Z) = 8
Case I: Points X, Y, Z are such that, X – Y – Z.
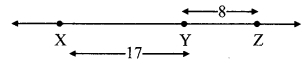
∴ d(X, Z) = d(X, Y) + d(Y, Z)
= 17 + 8
∴ d(X, Z) = 25
Case II: Points X, Y, Z are such that, X – Z – Y.
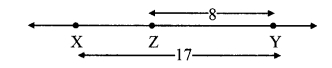
∴ d(X,Y) = d(X,Z) + d(Z,Y)
∴ 17 = d(X, Z) + 8
∴ d(X, Z) = 17 – 8
∴ d(X, Z) = 9
Case III: Points X, Y, Z are such that, Z – X – Y.
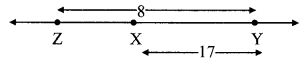
From the diagram,
d(X, Y) > d (Y, Z)
Which is not possible
∴ Point X is not between Z and Y.
∴ d(X, Z) = 25 or d(X, Z) = 9.
Question 6.
Sketch proper figure and write the answers of the following questions. [2 Marks each]
i. If A – B – C and l(AC) = 11,
l(BC) = 6.5, then l(AB) = ?
ii. If R – S – T and l(ST) = 3.7,
l(RS) = 2.5, then l(RT) = ?
iii. If X – Y – Z and l(XZ) = 3√7,
l(XY) = √7, then l(YZ) = ?
Solution:
i. Given, l(AC) =11, l(BC) = 6.5

l(AC) = l(AB) + l(BC) … [A – B – C]
∴ 11= l(AB) + 6.5
∴ l(AB) = 11 – 6.5
∴ l(AB) = 4.5
ii. Given, l(ST) = 3.7, l(RS) = 2.5
![]()
l(RT) = l(RS) + l(ST) … [R – S – T]
= 2.5 + 3.7
∴ (RT) = 6.2
iii. l(XZ) = 3√7 , l(XY) = √7,
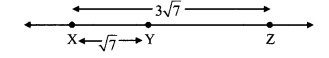
l(XZ) = l(X Y) + l(YZ) … [X – Y – Z]
∴ 3 √7 ⇒ √7 + l(YZ)
∴ l(YZ)= 3√7 – √7
∴ l(YZ) = 2 √7
Question 7.
Which figure is formed by three non-collinear points?
Solution:
Three non-collinear points form a triangle.