Balbharti Maharashtra State Board Class 6 Maths Solutions covers the Std 6 Maths Chapter 4 Operations on Fractions Class 6 Practice Set 13 Answers Solutions.
6th Standard Maths Practice Set 13 Answers Chapter 4 Operations on Fractions
Question 1.
Write the reciprocals of the following numbers:
- 7
- \(\frac { 11 }{ 3 }\)
- \(\frac { 5 }{ 13 }\)
- 2
- \(\frac { 6 }{ 7 }\)
Solution:
- \(\frac { 1 }{ 7 }\)
- \(\frac { 3 }{ 11 }\)
- \(\frac { 13 }{ 5 }\)
- \(\frac { 1 }{ 2 }\)
- \(\frac { 7 }{ 6 }\)
Question 2.
Carry out the following Divisions:
i. \(\frac{2}{3} \div \frac{1}{4}\)
ii. \(\frac{5}{9} \div \frac{3}{2}\)
iii. \(\frac{3}{7} \div \frac{5}{11}\)
iv. \(\frac{11}{12} \div \frac{4}{7}\)
Solution:
i. \(\frac{2}{3} \div \frac{1}{4}\)
![]()
ii. \(\frac{5}{9} \div \frac{3}{2}\)
![]()
iii. \(\frac{3}{7} \div \frac{5}{11}\)
![]()
iv. \(\frac{11}{12} \div \frac{4}{7}\)
![]()
Question 3.
There were 420 students participating in the Swachh Bharat Campaign. They cleaned \(\frac { 42 }{ 75 }\) part of the town, Sevagram. What part of Sevagram did each student clean if the work was equally shared by all?
Solution:
Total number of students = 420
Part of town cleaned by all the students = \(\frac { 42 }{ 75 }\)
∴ Part of town cleaned by one student
![]()
∴ Part of town cleaned bv one student is \(\frac { 1 }{ 750 }\)
Maharashtra Board Class 6 Maths Chapter 4 Operations on Fractions Practice Set 13 Intext Questions and Activities
Question 1.
Ramanujan’s Magic square. (Textbook pg. no. 28)
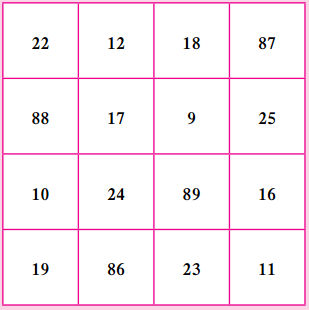
- Add the four numbers in the rows, the columns and along the diagonals of this square.
- What is the sum?
- Is it the same every time?
- What is the peculiarity?
- Look at the numbers in the first row, 22 – 12 – 1887. Find out why this date is special.
Obtain and read a biography of the great Indian mathematician Srinivasa Ramanujan.
Solution:
Sum of the numbers in each row:
i. 22 + 12 + 18 + 87 = 139
ii. 88 + 17 + 9 + 25 = 139
iii. 10 + 24 + 89 + 16 = 139
iv. 19 + 86 + 23 + 11 = 139
Sum of the numbers along the diagonals:
i. 22 + 17 + 89 + 11 = 139
ii. 87 + 9 + 24 + 19 = 139
Sum of the numbers in each column:
i. 22 + 88 + 10 + 19 = 139
ii. 12 + 17 + 24 + 86 = 139
iii. 18 + 9 + 89 + 23 = 139
iv. 87 + 25 + 16 + 11 = 139
∴ We observe that the sum of the numbers in each of the rows, the columns and along each diagonal remains the same every time. The numbers in the first row 22 – 12 – 1887 is the birth date of Srinivasa Ramanujan.