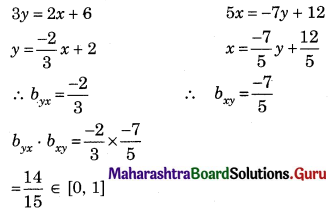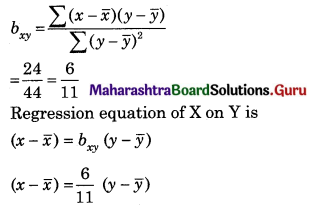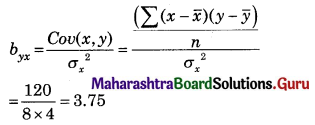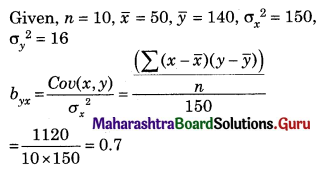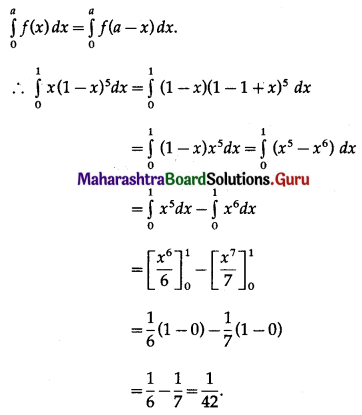Balbharati Maharashtra State Board 12th Commerce Maths Digest Pdf Chapter 3 Linear Regression Miscellaneous Exercise 3 Questions and Answers.
Maharashtra State Board 12th Commerce Maths Solutions Chapter 3 Linear Regression Miscellaneous Exercise 3
(I) Choose the correct alternative.
Question 1.
Regression analysis is the theory of
(a) Estimation
(b) Prediction
(c) Both a and b
(d) Calculation
Answer:
(c) Both a and b
Question 2.
We can estimate the value of one variable with the help of other known variable only if they are
(a) Correlated
(b) Positively correlated
(c) Negatively correlated
(d) Uncorrelated
Answer:
(a) Correlated
Question 3.
There are ________ types of regression equation
(a) 4
(b) 2
(c) 3
(d) 1
Answer:
(b) 2

Question 4.
In the regression equation of Y on X
(a) X is independent and Y is dependent
(b) Y is independent and X is dependent
(c) Both X and Y are independent
(d) Both X and Y are dependent.
Answer:
(a) X is independent and Y is dependent
Question 5.
In the regression equation of X on Y
(a) X is independent and Y is dependent
(b) Y is independent and X is dependent
(c) Both X and Y are independent
(d) Both X and Y are dependent
Answer:
(b) Y is independent and X is dependent
Question 6.
bxy is ________
(a) Regression coefficient of Y on X
(b) Regression coefficient of X on Y
(c) Correlation coefficient between X and Y
(d) Covariance between X and Y
Answer:
(b) Regression coefficient of X on Y
Question 7.
byx is ________
(a) Regression coefficient of Y on X
(b) Regression coefficient of X on Y
(c) Correlation coefficient between X and Y
(d) Covariance between X and Y
Answer:
(a) Regression coefficient of Y on X
Question 8.
‘r’ is ________
(a) Regression coefficient of Y on X
(b) Regression coefficient of X on Y
(c) Correlation coefficient between X and Y
(d) Covariance between X and Y
Answer:
(d) Correlation coefficient between X and Y

Question 9.
bxy . byx = _________
(a) v
(b) yx
(c) r2
(d) (yy)2
Answer:
(c) r2
Question 10.
If byx > 1 then bxy is ______
(a) > 1
(b) < 1
(c) > 0
(d) < 0
Answer:
(b) < 1
Question 11.
|bxy + byx| > ______
(a) |r|
(b) 2|r|
(c) r
(d) 2r
Answer:
(b) 2|r|
Question 12.
bxy and byx are ________
(a) Independent of change of origin and scale
(b) Independent of change of origin but not of the scale
(c) Independent of change of scale but not of origin
(d) Affected by change of origin and scale
Answer:
(b) Independent of change of origin but not of the scale
Question 13.
If u = \(\frac{x-a}{c}\) and v = \(\frac{y-b}{d}\) then byx = ________
(a) \(\frac{d}{c} b_{v u}\)
(b) \(\frac{c}{d} b_{v u}\)
(c) \(\frac{a}{b} b_{v u}\)
(d) \(\frac{b}{a} b_{v u}\)
Answer:
(a) \(\frac{d}{c} b_{v u}\)
Question 14.
If u = \(\frac{x-a}{c}\) and v = \(\frac{y-b}{d}\) then bxy = ________
(a) \(\frac{d}{c} b_{u v}\)
(b) \(\frac{c}{d} b_{u v}\)
(c) \(\frac{a}{b} b_{u v}\)
(d) \(\frac{b}{a} b_{u v}\)
Answer:
(b) \(\frac{c}{d} b_{u v}\)

Question 15.
Corr(x, x) = ________
(a) 0
(b) 1
(c) -1
(d) can’t be found
Answer:
(b) 1
Question 16.
Corr (x, y) = ________
(a) corr(x, x)
(b) corr(y, y)
(c) corr(y, x)
(d) cov(y, x)
Answer:
(c) corr(y, x)
Question 17.
Corr\(\left(\frac{x-a}{c}, \frac{y-b}{d}\right)\) = -corr(x, y) if,
(a) c and d are opposite in sign
(b) c and d are same in sign
(c) a and b are opposite in sign
(d) a and b are same in sign
Answer:
(a) c and d are opposite in sign
Question 18.
Regression equation of X and Y is
(a) y – \(\bar{y}\) = byx (x – \(\bar{x}\))
(b) x – \(\bar{x}\) = bxy (y – \(\bar{y}\))
(c) y – \(\bar{y}\) = bxy (x – \(\bar{x}\))
(d) x – \(\bar{x}\) = byx (y – \(\bar{y}\))
Answer:
(b) x – \(\bar{x}\) = bxy (y – \(\bar{y}\))
Question 19.
Regression equation of Y and X is
(a) y – \(\bar{y}\) = byx (x – \(\bar{x}\))
(b) x – \(\bar{x}\) = bxy (y – \(\bar{y}\))
(c) y – \(\bar{y}\) = bxy (x – \(\bar{x}\))
(d) x – \(\bar{x}\) = byx (y – \(\bar{y}\))
Solution:
(a) y – \(\bar{y}\) = byx (x – \(\bar{x}\))
Question 20.
byx = ________
(a) \(r \frac{\sigma_{x}}{\sigma_{y}}\)
(b) \(r \frac{\sigma_{y}}{\sigma_{x}}\)
(c) \(\frac{1 \sigma_{y}}{r \sigma_{x}}\)
(d) \(\frac{1 \sigma_{y}}{r \sigma_{y}}\)
Answer:
(b) \(r \frac{\sigma_{y}}{\sigma_{x}}\)
Question 21.
bxy = ________
(a) \(r \frac{\sigma_{x}}{\sigma_{y}}\)
(b) \(r \frac{\sigma_{y}}{\sigma_{x}}\)
(c) \(\frac{1 \sigma_{y}}{r \sigma_{x}}\)
(d) \(\frac{1 \sigma_{y}}{r \sigma_{y}}\)
Answer:
(a) \(r \frac{\sigma_{x}}{\sigma_{y}}\)
Question 22.
Cov (x, y) = ________
(a) Σ(x – \(\bar{x}\))(y – \(\bar{y}\))
(b) \(\frac{\sum(x-\bar{x})(y-\bar{y})}{n}\)
(c) \(\frac{\sum x y}{n}-\bar{x} \bar{y}\)
(d) b and c both
Answer:
(d) b and c both

Question 23.
If bxy < 0 and byx < 0 then ‘r’ is ________
(a) > 0
(b) < 0
(c) > 1
(d) not found
Answer:
(b) < 0
Question 24.
If equation of regression lines are 3x + 2y – 26 = 0 and 6x + y – 31 = 0 then means of x and y are ________
(a) (7, 4)
(b) (4, 7)
(c) (2, 9)
(d) (-4, 7)
Answer:
(b) (4, 7)
(II) Fill in the blanks:
Question 1.
If bxy < 0 and byx < 0 then ‘r’ is ________
Answer:
negative
Question 2.
Regression equation of Y on X is ________
Answer:
(y – \(\bar{y}\)) = byx (x – \(\bar{x}\))
Question 3.
Regression equation of X on Y is ________
Answer:
(x – \(\bar{x}\)) = bxy (y – \(\bar{y}\))
Question 4.
There are ______ types of regression equations.
Answer:
2
Question 5.
Corr (x1 – x) = ______
Answer:
-1
Question 6.
If u = \(\frac{x-a}{c}\) and v = \(\frac{y-b}{d}\) then bxy = ______
Answer:
\(\frac{c}{d} b_{u v}\)

Question 7.
If u = \(\frac{x-a}{c}\) and v = \(\frac{y-b}{d}\) then byx = ______
Answer:
\(\frac{d}{c} b_{v u}\)
Question 8.
|bxy + byx| ≥ ______
Answer:
2|r|
Question 9.
If byx > 1 then bxy is ______
Answer:
< 1
Question 10.
bxy . byx = ______
Answer:
r2
(III) State whether each of the following is True or False.
Question 1.
Corr (x, x) = 1.
Answer:
True
Question 2.
Regression equation of X on Y is y – \(\bar{y}\) = bxy (x – \(\bar{x}\)).
Answer:
False
Question 3.
Regression equation of Y on X is y – \(\bar{y}\) = byx (x – \(\bar{x}\)).
Answer:
True
Question 4.
Corr (x, y) = Corr (y, x).
Answer:
True
Question 5.
bxy and byx are independent of change of origin and scale.
Answer:
False
Question 6.
‘r’ is the regression coefficient of Y on X.
Answer:
False

Question 7.
byx is the correlation coefficient between X and Y.
Answer:
False
Question 8.
If u = x – a and v = y – b then bxy = buv.
Answer:
True
Question 9.
If u = x – a and v = y – b then rxy = ruv.
Answer:
True
Question 10.
In the regression equation of Y on X, byx represents the slope of the line.
Answer:
True
(IV) Solve the following problems.
Question 1.
The data obtained on X, the length of time in weeks that a promotional project has been in progress at a small business, and Y the percentage increase in weekly sales over the period just prior to the beginning of the campaign.
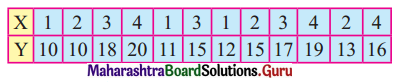
Find the equation of regression line to predict percentage increase in sales if the company has been in progress for 1.5 weeks.
Solution:
Let u = x – 3, v = y – 15
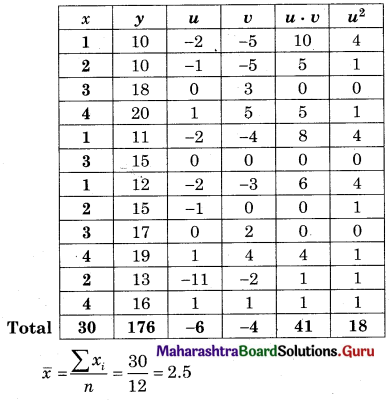

∴ Regression equation of Y on X is
(y – \(\bar{y}\)) = byx (x – \(\bar{x}\))
(y – 14.67) = 2.6(x – 2.5)
y – 14.67 = 2.6x – 6.5
y = 2.6x + 8.17
When x = 1.5
y = (2.6)(1.5) + 8.17
= 3.9 + 8.17
= 12.07
Question 2.
The regression equation of y on x is given by 3x + 2y – 26 = 0. Find byx.
Solution:
Given, regression equation of Y on X is
3x + 2y – 26 = 0
∴ 2y = -3x + 26
∴ y = \(\frac{-3}{2}\)x + 13
∴ byx = \(\frac{-3}{2}\)

Question 3.
If for a bivariate data \(\bar{x}\) = 10, \(\bar{y}\) = 12, v(x) = 9, σy = 4 and r = 0.6. Estimate y when x = 5.
Solution:
Given, V(x) = 9
∴ σx = 3
byx = \(\frac{r \cdot \sigma_{y}}{\sigma_{x}}\)
= 0.6 × \(\frac{4}{3}\)
= 0.8
∴ Regression equation of Y on X is
(y – \(\bar{y}\)) = byx (x – \(\bar{x}\))
(y – 12) = 0.8(5 – 10)
y – 12 = 0.8(-5)
y – 12 = -4
y = 8
Question 4.
The equation of the line of regression of y on x is v = \(\frac{2}{9} x\) and x on y is x = \(\frac{y}{2}+\frac{7}{6}\). Find (i) r (ii) \(\sigma_{y}^{2} \text { if } \sigma_{x}^{2}=4\).
Solution:

Question 5.
Identify the regression equations of x on y and y on x from the following equations.
2x + 3y = 6 and 5x + 7y – 12 = 0
Solution:
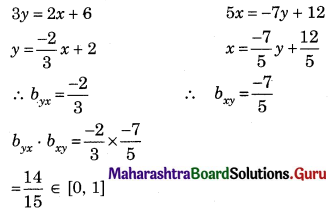
∴ Our assumption is correct
∴ Regression equation of Y on X is 2x + 3y = 6
∴ Regression equation of X on Y is 5x + 7y – 12 = 0
Question 6.
(i) If for a bivariate data byx = -1.2 and bxy = -0.3 then find r.
(ii) From the two regression equations y = 4x – 5 and 3x = 2y + 5, find \(\bar{x}\) and \(\bar{y}\).
Solution:
r2 = byx . bxy
r2 = (-1.2) × (-0.3)
r2 = 0.36
r = ±0.6
Since, byx . bxy are negative, r = -0.6
Also,(\(\bar{x}\), \(\bar{y}\)) is the point of intersection of the regression lines
y = 4x – 5, 3x = 2y + 5
8x – 2y = 10
3x – 2y = 5
on subtracting,
5x = 5
x = 1
Substituting x = 1 in y = 4x – 5
y = 4(1) – 5
y = -1
∴ \(\bar{x}\) = 1, \(\bar{y}\) = -1

Question 7.
The equation of the two lines of regression are 3x + 2y – 26 = 0 and 6x + y – 31 = 0. Find
(i) Means of X and Y
(ii) Correlation coefficient between X on Y
(iii) Estimate of Y for X = 2
(iv) var (X) if var (Y) = 36
Solution:
(i) Since (\(\bar{x}\), \(\bar{y}\)) is the point of intersection of regression lines
3x + 2y = 26
6x + y = 31
3x + 2y = 26 …….(i)
12x + 2y = 62 ……..(ii)
on subtracting,
-9x = -36
x = 4
Substituting x = 4 in equation (i)
3(4) + 2y = 26
2y = 14
y = 7
∴ \(\bar{x}\) = 4, \(\bar{y}\) = 7


Question 8.
Find the line of regression of X on Y for the following data:
n = 8, Σ(xi – x)2 = 36, Σ(yi – y)2 = 44, Σ(xi – x)(yi – y) = 24
Solution:
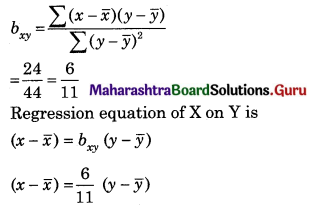
Question 9.
Find the equation of line regression of Y on X for the following data:
n = 8, Σ(xi – \(\bar{x}\))(yi – \(\bar{y}\)) = 120, \(\bar{x}\) = 20, \(\bar{y}\) = 36, σx = 2, σy = 3.
Solution:
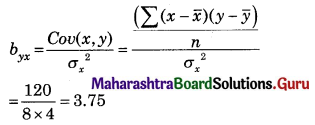
Regression equation of Y on X is
(y – \(\bar{y}\)) = byx (x – \(\bar{x}\))
(y – 36) = 3.75(x – 20)
(y – 36) = 3.75x – 75
y = 3.75x – 39

Question 10.
The following result was obtained from records of age (X) and systolic blood pressure (Y) of a group of 10 men.
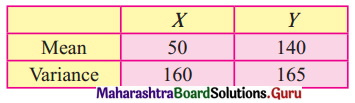
and Σ(xi – \(\bar{x}\))(yi – \(\bar{x}\)) = 1120. Find the Prediction of blood pressure of a man of age 40 years.
Solution:
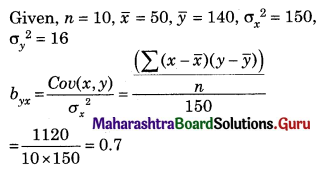
Regression equation of Y on X is
(y – \(\bar{y}\)) = byx (x – \(\bar{x}\))
(y – 140) = 0.7(40 – 50)
y – 140 = 0.7(-10)
y – 140 = -7
∴ y = 133
Question 11.
The equations of two regression lines are 10x – 4y = 80 and 10y – 9x = -40 Find:
(i) \(\bar{x}\) and \(\bar{y}\)
(ii) byx and bxy
(iii) If var(Y) = 36, obtain var(X)
(iv) r
Solution:
(i) Since (\(\bar{x}\), \(\bar{y}\)) is the point of intersection of regression
10x – 4y = 80 ……(i)
-9x + 10y = -40 ……..(ii)
50x – 20y = 400
-18x + 20y = -80
32x = 320
x = 10
x = 10 in equation (i)
10(10) – 4y = 80
4y = 20
y = 5
∴ \(\bar{x}\) = 10, \(\bar{y}\) = 5


(iv) r2 = byx . bxy = 0.36
r = ±0.6
Since byx and bxy are positive
∴ r = 0.6

Question 12.
If byx = -0.6 and bxy = -0.216 then find correlation coefficient between X and Y comment on it.
Solution:
r2 = byx . bxy
r2 = -0.6 × -0.216
r2 = 0.1296
r = ±√0.1296
r = ± 0.36
Since byx and bxy are negative
r = -0.36
![]()

![]()
![]()