Class 12

Balbharati Maharashtra State Board 12th Commerce Maths Solution Book Pdf Chapter 5 Index Numbers Ex 5.1 Questions and Answers.

Maharashtra State Board 12th Commerce Maths Solutions Chapter 5 Index Numbers Ex 5.1

Find the Price Index Number using the Simple Aggregate Method in each of the following examples.

Question 1.
Use 1995 as the base year in the following problem.

Solution:

Question 2.
Use 1995 as the base year in the following problem.

Solution:

Question 3.

Solution:

Question 4.
Use 2000 as the base year in the following problem.

Solution:

Question 5.
Use 1990 as the base year in the following problem.

Solution:

Question 6.
Assume 2000 to be a base year in the following problem.

Solution:

Question 7.
Use 2005 as a year in the following problem.

Solution:

Find the Quantity Index Number using the Simple Aggregate Method in each of the following examples.

Question 8.

Solution:

Question 9.

Solution:

Find the value Index Number using the Simple Aggregate Method in each of the following examples.

Question 10.

Solution:

= \(\frac{3660}{2840}\) × 100
= 128.87

Question 11.

Solution:

Question 12.
Find x if the Price Index Number by Simple Aggregate Method is 125

Solution:

Question 13.
Find y is the Price Index Number by Simple Aggregate Method is 120, taking 1995 as the base year.

Solution:

Balbharati Maharashtra State Board 12th Commerce Maths Digest Pdf Chapter 3 Linear Regression Ex 3.3 Questions and Answers.

Maharashtra State Board 12th Commerce Maths Solutions Chapter 3 Linear Regression Ex 3.3

Question 1.
From the two regression equations find r, \(\bar{x}\) and \(\bar{y}\).
4y = 9x + 15 and 25x = 4y + 17
Solution:
Given 4y = 9x + 15 and 25x = 4y + 17

Since b_yx and b_xy are positive.
∴ r = \(\frac{3}{5}\) = 0.6
(\(\bar{x}\), \(\bar{y}\)) is the point of intersection of the regression lines
9x – 4y = -15 …….(i)
25x – 4y = 17 ……….(ii)
-16x = -32
x = 2
∴ \(\bar{x}\) = 2
Substituting x = 2 in equation (i)
9(2) – 4y = -15
18 + 15 = 4y
33 = 4y
y = 33/4 = 8.25
∴ \(\bar{y}\) = 8.25

Question 2.
In a partially destroyed laboratory record of an analysis of regression data, the following data are legible:
Variance of X = 9
Regression equations:
8x – 10y + 66 = 0 And 40x – 18y = 214.
Find on the basis of the above information
(i) The mean values of X and Y.
(ii) Correlation coefficient between X and Y.
(iii) Standard deviation of Y.
Solution:
Given, \(\sigma_{x}{ }^{2}=9, \sigma_{x}=3\)
(i) (\(\bar{x}\), \(\bar{y}\)) is the point of intersection of the regression lines
40x – 50y = -330 …….(i)
40x – 50y = +214 ………(ii)
-32y = -544
y = 17
∴ \(\bar{y}\) = 17
8x – 10(17) + 66 = 0
8x = 104
x = 13
∴ \(\bar{x}\) = 13

Question 3.
For 50 students of a class, the regression equation of marks in statistics (X) on the marks in Accountancy (Y) is 3y – 5x + 180 = 0. The mean marks in accountancy is 44 and the variance of marks in statistics \(\left(\frac{9}{16}\right)^{t h}\) of the variance of marks in accountancy. Find the mean in statistics and the correlation coefficient between marks in two subjects.
Solution:
Given, n = 50, \(\bar{y}\) = 44
\(\sigma_{x}^{2}=\frac{9}{16} \sigma_{y}^{2}\)
∴ \(\frac{\sigma_{x}}{\sigma_{x}}=\frac{3}{4}\)
Since (\(\bar{x}\), \(\bar{y}\)) is the point intersection of the regression line.
∴ (\(\bar{x}\), \(\bar{y}\)) satisfies the regression equation.
3\(\bar{y}\) – 5\(\bar{x}\) + 180 = 0
3(44) – 5\(\bar{x}\) + 180 = 0
∴ 5\(\bar{x}\) = 132 + 180
\(\bar{x}\) = \(\frac{312}{5}\) = 62.4
∴ Mean marks in statistics is 62.4
Regression equation of X on Y is 3y – 5x + 180 = 0
∴ 5x = 3y + 180

Question 4.
For bivariate data, the regression coefficient of Y on X is 0.4 and the regression coefficient of X on Y is 0.9. Find the value of the variance of Y if the variance of X is 9.
Solution:

Question 5.
The equation of two regression lines are 2x + 3y – 6 = 0 and 3x + 2y – 12 = 0
Find (i) Correlation coefficient (ii) \(\frac{\sigma_{x}}{\sigma_{y}}\)
Solution:

Question 6.
For a bivariate data \(\bar{x}\) = 53, \(\bar{y}\) = 28, b_yx =-1.5 and b_xy = -0.2. Estimate Y when X = 50.
Solution:
Regression equation of Y on X is
(Y – \(\bar{y}\)) = b_yx (X – \(\bar{x}\))
(Y – 28) = -1.5(50 – 53)
Y – 28 = -1.5(-3)
Y – 28 = 4.5
Y = 32.5

Question 7.
The equation of two regression lines are x – 4y = 5 and 16y – x = 64. Find means of X and Y. Also, find the correlation coefficient between X and Y.
Solution:
Since (\(\bar{x}\), \(\bar{y}\)) is the point of intersection of the regression lines.
x – 4y = 5 …..(i)
-x + 16y = 64 …….(ii)
12y = 69
y = 5.75
Substituting y = 5.75 in equation (i)
x – 4(5.75) = 5
x – 23 = 5
x = 28
∴ \(\bar{x}\) = 28, \(\bar{y}\) = 5.75
x – 4y = 5
x = 4y + 5
∴ b_xy = 4
16y – x = 64
16y = x + 64
y = \(\frac{1}{16}\)x + 4
b_yx = \(\frac{1}{16}\)
b_yx . b_xy = \(\frac{1}{16}\) × 4 = \(\frac{1}{4}\) ∈ [0, 1]
∴ Our assumption is correct
∴ r² = b_yx . b_xy
r² = \(\frac{1}{4}\)
r = ±\(\frac{1}{2}\)
Since b_yx and b_xy are positive,
∴ r = \(\frac{1}{2}\) = 0.5

Question 8.
In partially destroyed record, the following data are available variance of X = 25. Regression equation of Y on X is 5y – x = 22 and Regression equation of X on Y is 64x – 45y = 22 Find
(i) Mean values of X and Y.
(ii) Standard deviation of Y.
(iii) Coefficient of correlation between X and Y.
Solution:
Given \(\sigma_{x}^{2}\) = 25, ∴ σ_x = 5
(i) Since (\(\bar{x}\), \(\bar{y}\)) is the point of intersection of regression lines
-x + 5y = 22 …….(i)
64x – 45y = 22 ………..(ii)
equation (i) becomes
-9x + 45y = 198
64y – 45y = 22
55x = 220
x = 4
Substituting x = 4 in equation (i)
-4 + 5y = 22
5y = 26
∴ y = 5.2
∴ \(\bar{x}\) = 4, \(\bar{y}\) = 5.2
Regression equation of X on Y is
64x – 45y – 22
64x = 45y + 22
x = \(\frac{45}{64} y+\frac{22}{64}\)
bxy = \(\frac{45}{64}\)
(ii) Regression equation of Y on X is
5y – x = 22
5y = x + 22

Question 9.
If the two regression lines for a bivariate data are 2x = y + 15 (x on y) and 4y – 3x + 25 (y on x) find
(i) \(\bar{x}\)
(ii) \(\bar{y}\)
(iii) b_yx
(iv) b_xy
(v) r [Given √0.375 = 0.61]
Solution:
Since (\(\bar{x}\), \(\bar{y}\)) is the point of intersection of the regression line
2x = y + 15
4y = 3x + 25
2x – y = 15 …….(i)
3x – 4y = -25 ……..(ii)
Multiplying equation (i) by 4
8x – 4y = 60
3x – 4y = -25
on Subtracting,
5x = 85
∴ x = 17
Substituting x in equation (i)
2(17) – y = 15
34 – 15 = y
∴ y = 15

Since b_yx and b_xy are positive, ∴ r = 0.61

Question 10.
The two regression equation are 5x – 6y + 90 = 0 and 15x – 8y – 130 = 0. Find \(\bar{x}\), \(\bar{y}\), r.
Solution:
Since (\(\bar{x}\), \(\bar{y}\)) is the point of intersection of the regression lines
5x – 6y + 90 = 0 ……(i)
15x – 8y – 130 = 0
15x – 18y + 270 = 0
15x – 8y – 130 = 0
on subtracting,
-10y + 400 = 0
y = 40
Substituting y = 40 in equation (i)
5x – 6(40) + 90 = 0
5x = 150
x = 30
∴ \(\bar{x}\) = 30, \(\bar{y}\) = 40

Since b_yx and b_xy are positive
∴ r = \(\frac{2}{3}\)

Question 11.
Two lines of regression are 10x + 3y – 62 = 0 and 6x + 5y – 50 = 0 Identify the regression equation equation of x on y. Hence find \(\bar{x}\), \(\bar{y}\), and r.
Solution:

∴ Our assumption is correct.
∴ Regression equation of X on Y is 10x + 3y – 62 = 0
r² = b_yx . b_xy
r² = \(\frac{9}{25}\)
r = ±\(\frac{3}{5}\)
Since, byx and bxy are negative, r = –\(\frac{3}{5}\) = -0.6
Also (\(\bar{x}\), \(\bar{y}\)) is the point of intersection of the regression lines
50x + 15y = 310
18x + 15y = 150
on subtracting
32x = 160
x = 5
Substituting x = 5 in 10x + 3y = 62
10(5) + 3y = 62
3y = 12
∴ y = 4
∴ \(\bar{x}\) = 5, \(\bar{y}\) = 4

Question 12.
For certain X and Y series, which are correlated the two lines of regression are 10y = 3x + 170 and 5x + 70 = 6y. Find the correlation coefficient between them. Find the mean values of X and Y.
Solution:

Since byx and bxy are positive,
r = \(\frac{3}{5}\) = 0.6
Since, (\(\bar{x}\), \(\bar{y}\)) is the point of intersection of the regression lines
3x – 10y = -170 …….(i)
5x – 6y = -70 ………(ii)
9x – 30y = -510
25x – 30y = -350
on subtracting
-16x = -160
x = 10
Substituting x = 10 in equation (i)
3(10) – 10y = -170
30 + 170 = 10y
200 = 10y
y = 20
∴ \(\bar{x}\) = 10, \(\bar{y}\) = 20

Question 13.
Regression equation of two series are 2x – y – 15 = 0 and 4y + 25 = 0 and 3x- 4y + 25 = 0. Find \(\bar{x}\), \(\bar{y}\) and regression coefficients, Also find coefficients of correlation. [Given √0.375 = 0.61]
Solution:
Since (\(\bar{x}\), \(\bar{y}\)) is the point of intersection of the regression line
2x = y + 15
4y = 3x + 25
2x – y = 15 ……(i)
3x – 4y = -15 ……..(ii)
Multiply equation (i) by 4
8x – 4y = 60
3x – 4y = -25
on subtracting,
5x = 85
x = 17
Substituting x in equation (i)
2(17) – y = 15
34 – 15 = y
y = 15
∴ \(\bar{x}\) = 17, \(\bar{y}\) = 19

∴ Our assumption is correct
r² = b_xy . b_yx
r² = \(\frac{3}{8}\) = 0.375
r = ±√o.375 = ±0.61
Since, b_yx and b_xy are positive, ∴ r = 0.61

Question 14.
The two regression lines between height (X) in includes and weight (Y) in kgs of girls are 4y – 15x + 500 = 0 and 20x – 3y – 900 = 0. Find the mean height and weight of the group. Also, estimate the weight of a girl whose height is 70 inches.
Solution:
Since (\(\bar{x}\), \(\bar{y}\)) is the point intersection of the regression lines
15x – 4y = 500 ……(i)
20x – 3y = 900 …….(ii)
60x – 16y – 2000
60x – 9y = 2700
on subtracting,
-7y = -700
y = 100
Substituting y = 100 in equation (i)
15x – 4(100) = 500
15x = 900
x = 60

∴ Our assumption is correct
∴ Regression equation of Y on X is
Y = \(\frac{15}{4}\)x – 125
When x = 70
Y = \(\frac{15}{4}\) × 70 = -125
= 262.5 – 125
= 137.5 kg

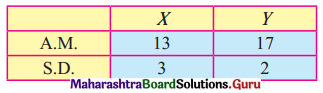
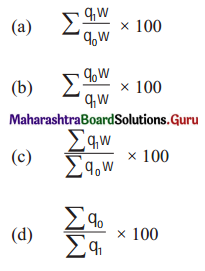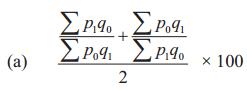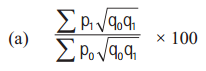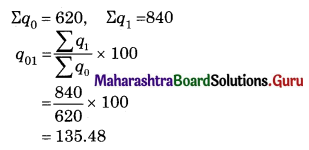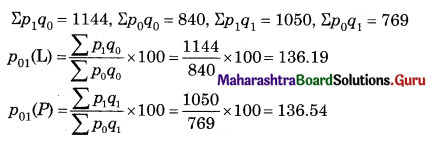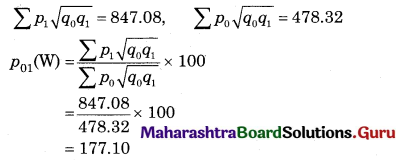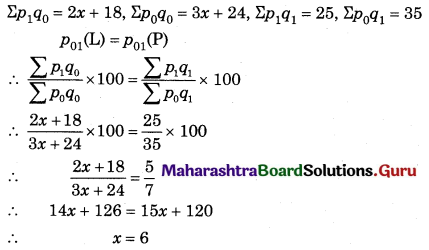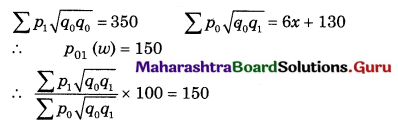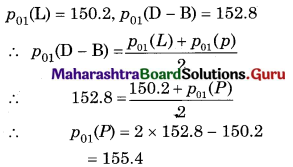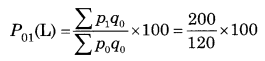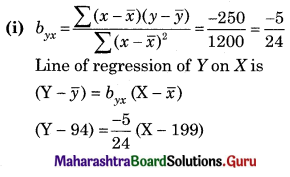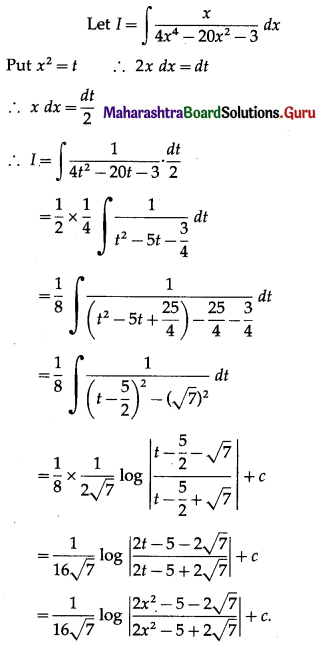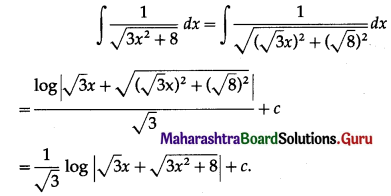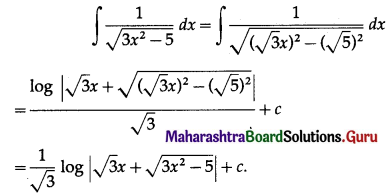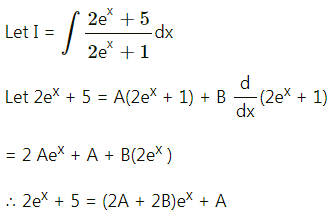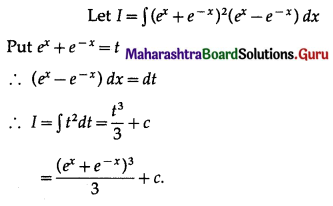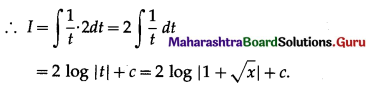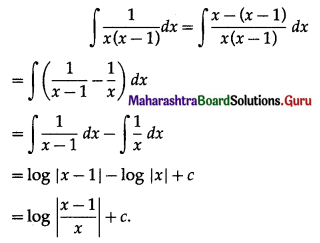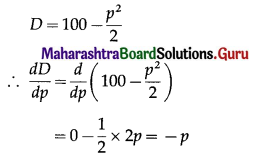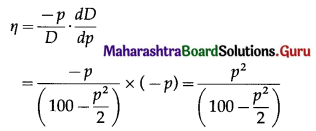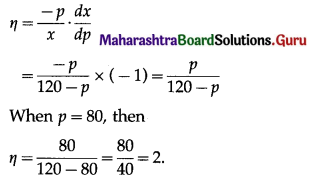Balbharati Maharashtra State Board 12th Commerce Maths Solution Book Pdf Chapter 5 Index Numbers Miscellaneous Exercise 5 Questions and Answers.

Maharashtra State Board 12th Commerce Maths Solutions Chapter 5 Index Numbers Miscellaneous Exercise 5

(I) Choose the correct alternative.

Question 1.
Price Index Number by Simple Aggregate method is given by

Answer:
(c) \(\frac{\sum p_{1}}{\sum p_{0}} \times 100\)

Question 2.
Quantity Index Number by Simple Aggregate Method is given by

Answer:
(c) \(\frac{\sum q_{1}}{\sum q_{0}} \times 100\)

Question 3.
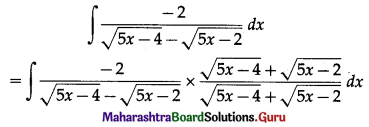
Value Index Number by Simple Aggregate Method is given by

Answer:
(b) \(\sum \frac{p_{0} q_{1}}{p_{0} q_{0}} \times 100\)

Question 4.
Price Index Number by Weighted Aggregate Method is given by

Answer:
(c) \(\frac{\sum p_{1} w}{\sum p_{0} w} \times 100\)

Question 5.
Quantity Index Number By Weighted Aggregate Method is given by

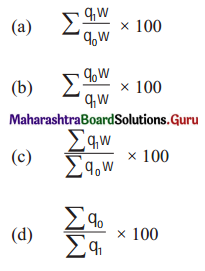
Answer:
(c) \(\frac{\sum q_{1} w}{\sum q_{0} w} \times 100\)

Question 6.
Value Index Number by Weighted aggregate Method is given by

Answer:
(d) \(\frac{\sum p_{1} q_{1} w}{\sum p_{0} q_{0} w} \times 100\)

Question 7.
Laspeyre’s Price Index Number is given by

Answer:
(c) \(\frac{\sum p_{1} q_{0}}{\sum p_{0} q_{0}} \times 100\)

Question 8.
Paassche’s Price Index Number is given by

Answer:
(d) \(\frac{\sum p_{1} q_{1}}{\sum p_{0} q_{1}} \times 100\)

Question 9.
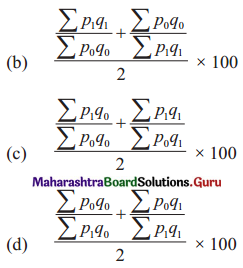
Dorbish-Bowley’s Price Index Number is given by


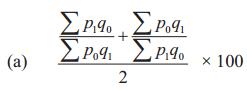
Answer:
(c) \(\frac{\frac{\sum p_{1} q_{0}}{\sum p_{0} q_{0}}+\frac{\sum p_{1} q_{1}}{\sum p_{0} q_{1}}}{2} \times 100\)

Question 10.
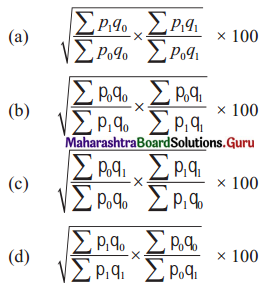
Fisher’s Price Number is given by

Answer:
(a) \(\sqrt{\frac{\sum p_{1} q_{0}}{\sum p_{0} q_{0}} \times \frac{\sum p_{1} q_{1}}{\sum p_{0} q_{1}}} \times 100\)

Question 11.
Marshall-Edge worth’s Price Index Number is given by

Answer:
(a) \(\frac{\sum p_{1}\left(q_{0}+q_{1}\right)}{\sum p_{0}\left(q_{0}+q_{1}\right)} \times 100\)

Question 12.
Walsh’s Price Index Number is given by


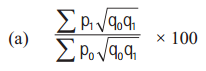
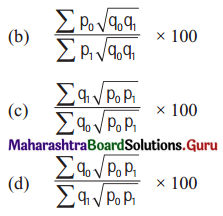
Answer:
(a) \(\frac{\sum p_{1} \sqrt{q_{0} q_{1}}}{\sum p_{0} \sqrt{q_{0} q_{1}}} \times 100\)

Question 13.
The Cost of Living Index Number using Aggregate Expenditure Method is given by

Answer:
(a) \(\frac{\sum p_{1} q_{0}}{\sum p_{0} q_{0}} \times 100\)

Question 14.
The Cost of Living Index Number using Weighted Relative Method is given by

Answer:
(a) \(\frac{\sum \mathrm{IW}}{\sum \mathrm{W}}\)

(II) Fill in the blanks.

Question 1.
Price Index Number by Simple Aggregate Method is given by ____________
Answer:
\(\frac{\sum p_{1}}{\sum p_{0}} \times 100\)

Question 2.
Quantity Index number by Simple Aggregate Method is given by ____________
Answer:
\(\frac{\sum q_{1}}{\sum q_{0}} \times 100\)

Question 3.
Value Index Number by Simple Aggregate Method is given by ____________
Answer:
\(\frac{\sum p_{1} q_{1}}{\sum p_{0} q_{0}} \times 100\)

Question 4.
Price Index Number by Weighted Aggregate Method is given by ____________
Answer:
\(\frac{\sum p_{1} w}{\sum p_{0} w} \times 100\)

Question 5.
Quantity Index Number by Weighted Aggregate Method is given by ____________
Answer:
\(\frac{\sum q_{1} w}{\sum q_{0} w} \times 100\)

Question 6.
Value Index Number by Weighted Aggregate Method is given by ____________
Answer:
\(\frac{\sum p_{1} q_{1} w}{\sum p_{0} q_{0} w} \times 100\)

Question 7.
Laspeyre’s Price Index Number is given by ____________
Answer:
\(\frac{\sum p_{1} q_{0}}{\sum p_{0} q_{0}} \times 100\)

Question 8.
Paasche’s Price Index Number is given by ____________
Answer:
\(\frac{\sum p_{1} q_{1}}{\sum p_{0} q_{1}} \times 100\)

Question 9.
Dorbish-Bowley’s Price Index Number is given by ____________
Answer:
\(\frac{1}{2}\left[\frac{\sum p_{1} q_{0}}{\sum p_{0} q_{0}}+\frac{\sum p_{1} q_{1}}{\sum p_{0} q_{1}}\right] \times 100\)

Question 10.
Fisher’s Price Index Number is given by ____________
Answer:
\(\sqrt{\left[\frac{\sum p_{1} q_{0}}{\sum p_{0} q_{0}} \times \frac{\sum p_{1} q_{1}}{\sum p_{0} q_{1}}\right]} \times 100\)

Question 11.
Marshall-Edgeworth’s Price Index Number is given my ____________
Answer:
\(\frac{\sum p_{1}\left(q_{0}+q_{1}\right)}{\sum p_{0}\left(q_{0}+q_{1}\right)} \times 100\)

Question 12.
Walsh’s Price Index Number is given by ____________
Answer:
\(\frac{\sum p_{1} \sqrt{q_{0} q_{1}}}{\sum p_{0} \sqrt{q_{0} q_{1}}} \times 100\)

(III) State whether each of the following is True or False.

Question 1
\(\frac{\sum p_{1}}{\sum p_{0}} \times 100\) is the Price Index Number by Simple Aggregate Method.
Answer:
True

Question 2
\(\frac{\sum q_{0}}{\sum q_{1}} \times 100\) is the Quantity Index Number by Simple Aggregate Method.
Answer:
False

Question 3.
\(\sum \frac{p_{0} q_{0}}{p_{1} q_{1}} \times 100\) is value Index Number by Simple Aggregate Method.
Answer:
False

Question 4.
\(\sum \frac{p_{1} q_{0}}{p_{1} q_{1}} \times 100\) Paasche’s Price Index Number.
Answer:
False

Question 5.
\(\frac{\sum p_{1} q_{1}}{\sum p_{0} q_{1}} \times 100\) is Laspeyre’s Price Index Number.
Answer:
False

Question 6.
\(\frac{\sum p_{1} q_{0}}{\sum p_{0} q_{0}} \times \frac{\sum p_{1} q_{0}}{\sum p_{0} q_{0}} \times 100\) is Dorbish-Bowley’s Index Number.
Answer:
False

Question 7.
\(\frac{1}{2}\left[\sqrt{\frac{\sum p_{1} q_{0}}{\sum p_{0} q_{0}}}+\frac{\sqrt{p_{1} q_{1}}}{\sqrt{p_{0} q_{1}}}\right] \times 100\) is Fisher’s Price Index Number.
Answer:
False

Question 8.
\(\frac{\sum p_{0}\left(q_{0}+q_{1}\right)}{\sum p_{1}\left(q_{0}+q_{1}\right)} \times 100\) is Marshall-Edgeworth’s Index Number.
Answer:
False

Question 9.
\(\frac{\sum p_{0} \sqrt{q_{0} q_{1}}}{\sum p_{1} \sqrt{q_{0} q_{1}}} \times 100\) is Walsh’s Price Index Number.
Answer:
False

Question 10.
\(\sqrt{\frac{\sum p_{1} q_{0}}{\sum p_{0} q_{0}}} \times \sqrt{\frac{\sum p_{1} q_{1}}{\sum p_{0} q_{1}}} \times 100\) is Fisher’s Price Index Number.
Answer:
True

(IV) Solve the following problems.

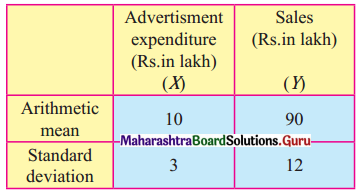
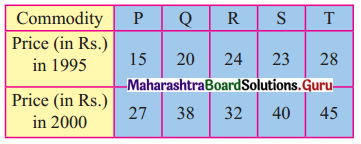
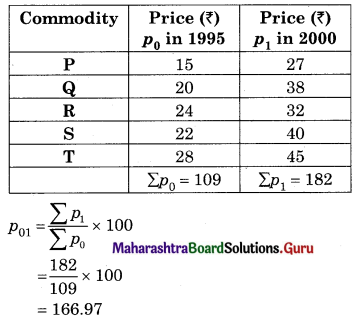
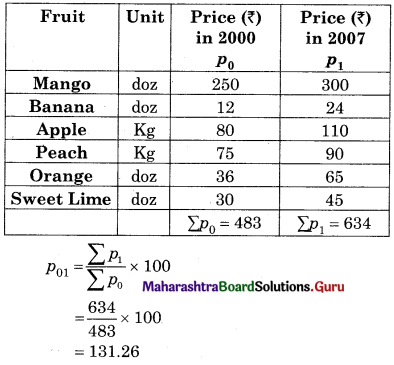
Question 1.
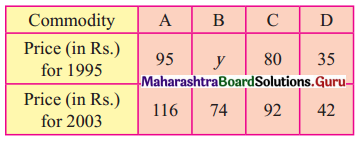
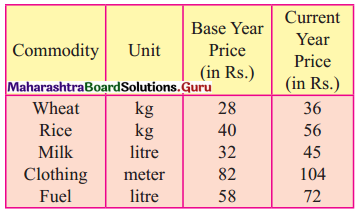
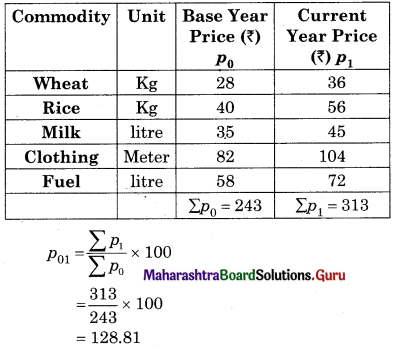
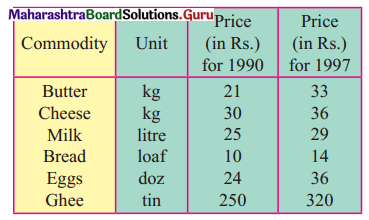
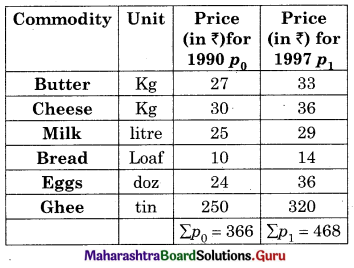
Find the price Index Number using simple Aggregate Method Consider 1980 as base year.

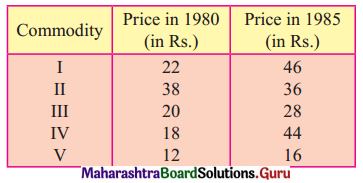
Solution:

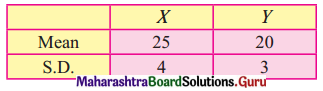
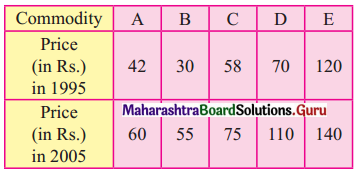
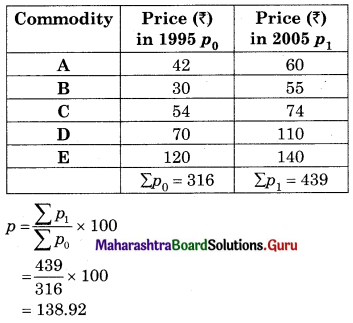
Question 2.
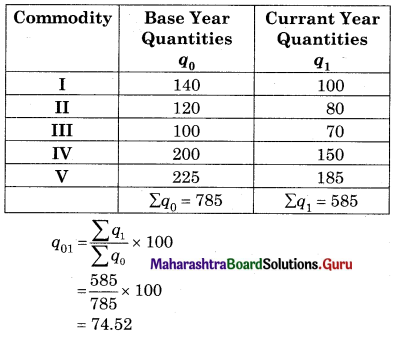
Find the Quantity Index Number using Simple Aggregate Method.

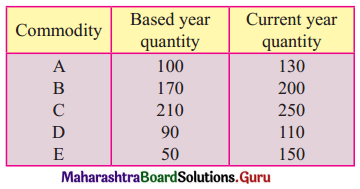
Solution:

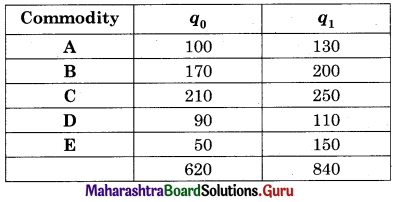
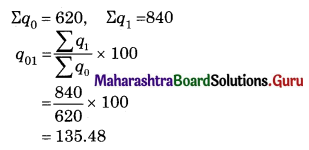
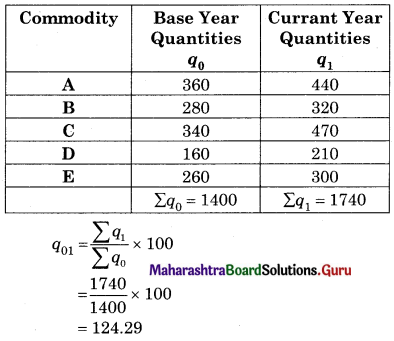
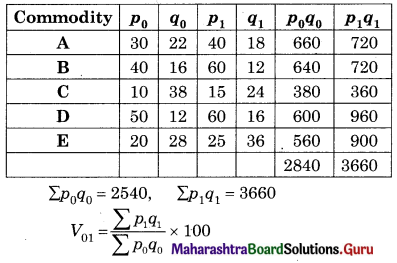
Question 3.
Find the Value Index Number using Simple Aggregate Method.

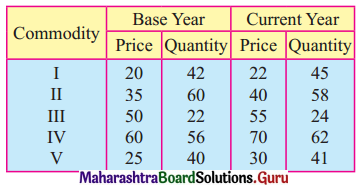
Solution:

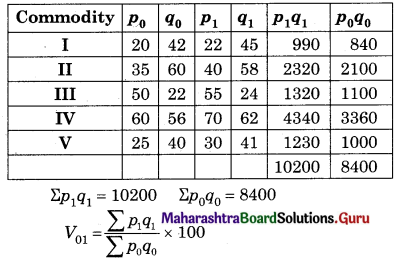
= \(\frac{10200}{8400}\) × 100
= 121.43

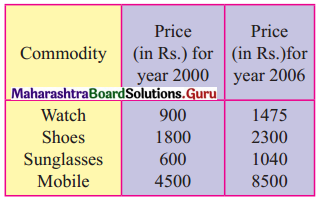
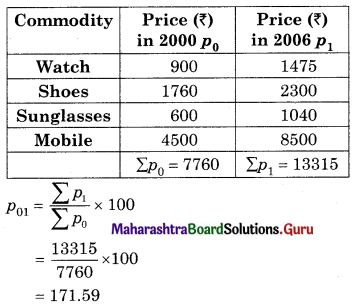
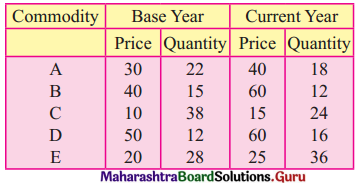
Question 4.
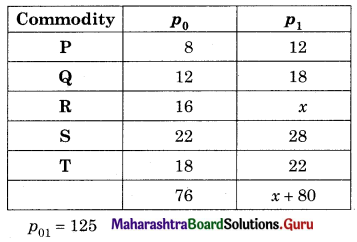
Find x if the Price Index Number using Simple Aggregate Method is 200.

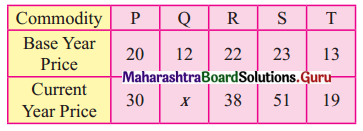
Solution:

Question 5.
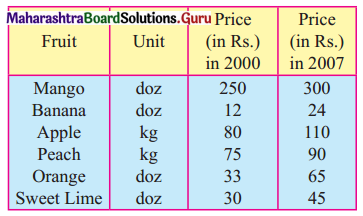
Calculate Laspeyre’s and Paasche’s Price Index Number for the following data.

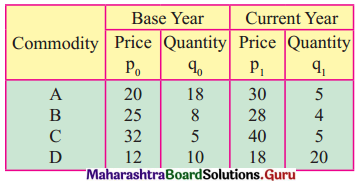
Solution:

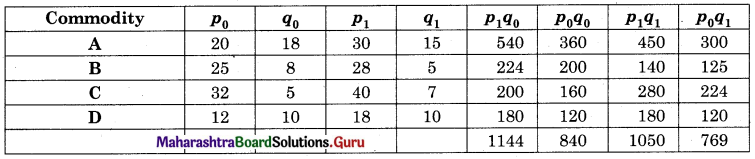
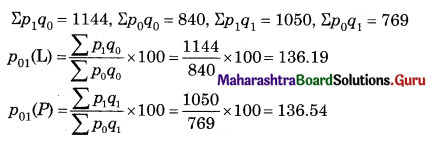
Question 6.
Calculate Dorbish-Bowley’s Price Index Number for the following data.

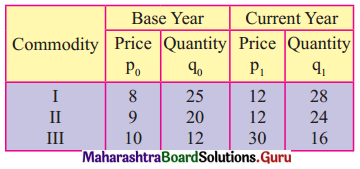
Solution:

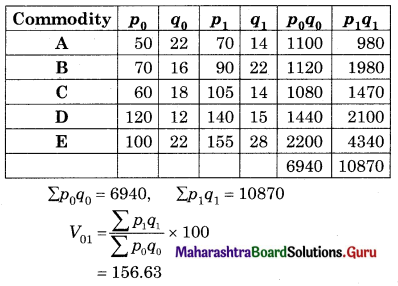
Question 7.
Calculate Marshall-Edge worth’s Price Index Number for the following data.

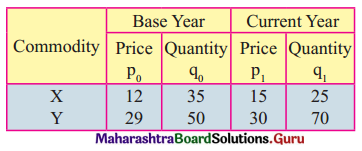
Solution:

Question 8.
Calculate Walsh’s Price Index Number for the following data.

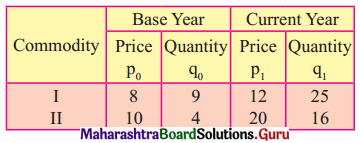
Solution:

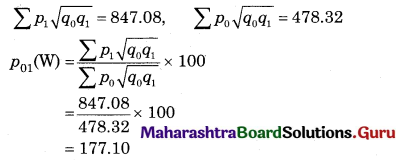
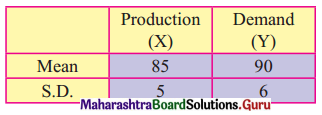
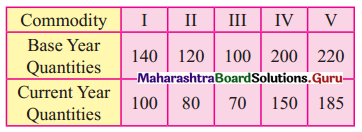
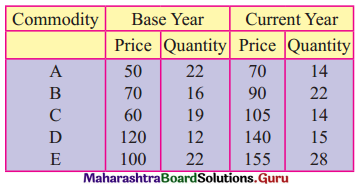
Question 9.
Calculate Laspeyre’s Price Index Number for the following data.

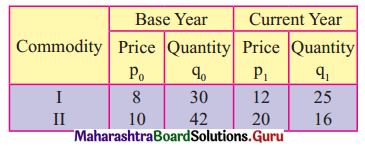
Solution:

Question 10.
Find x if Laseyre’s Price Index Number is same as Paasche’s Price Index Number for the following data.

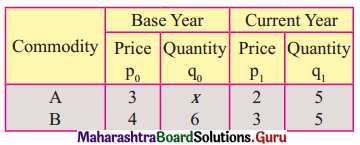
Solution:

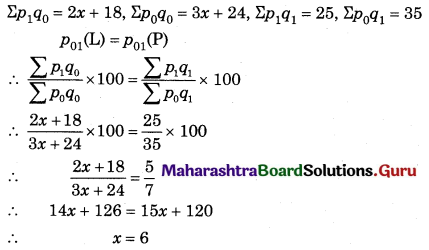
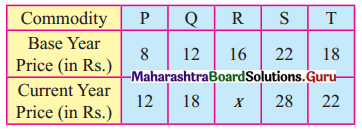
Question 11.
Find x if Walsh’s Price Index Number is 150 for the following data.

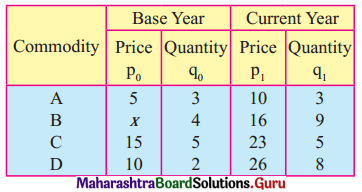
Solution:

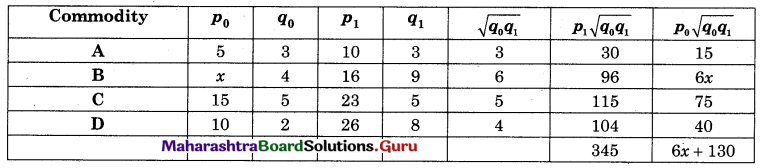
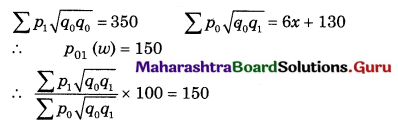
Question 12.
Find x if Paasche’s Price Index Number is 140 for the following data.

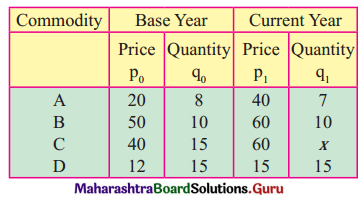
Solution:

Question 13.
Given that Laspeyre’s and Paasche’s Index Number are 25 and 16 respectively. Find Dorbish-Bowley’s and Fisher’s Price Index Number.
Solution:

= \(\sqrt{25 \times 16}\)
= 20

Question 14.
If Laspeyre’s and Dorbish Price Index Number are 150.2 and 152.8 respectively, find Paasche’s rice Index Number.
Solution:

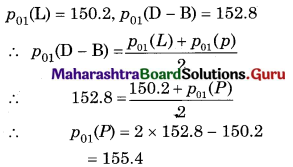
Question 15.
If Σp₀q₀ = 120, Σp₀q₁ = 160, Σp₁q₁ = 140, and Σp₁q₀ = 200 find Laspeyre’s, Paasche’s, Dorbish-Bowley’s, and Marshall-Edgeworth’s Price Index Numbers.
Solution:

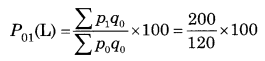
Question 16.
Given that Σp₀q₀ = 130, Σp₁q₁ = 140, Σp₀q₁ = 160, and Σp₁q₀ = 200, find Laspeyare’s, Passche’s, Dorbish-Bowely’s and Mashall-Edegeworth’s Price Inbox Numbers.
Solution:

Question 17.
Given that Σp₁q₁ = 300, Σp₀q₁ = 140, Σp₀q₀ = 120, and Marshall-Edegeworth’s Price Inbox Number is 120, find Laspeyre’s Price Index Number.
Solution:
p₀₁(P) = \(\frac{\sum p_{1} q_{1}}{\sum p_{0} q_{1}} \times 100\)
= \(\frac{300}{320}\) × 100
= 93.75

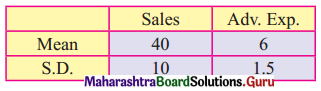
Question 18.
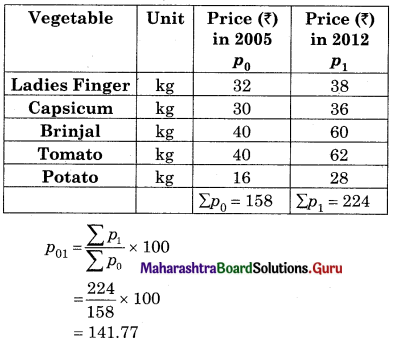
Calculate the cost of living number for the following data.

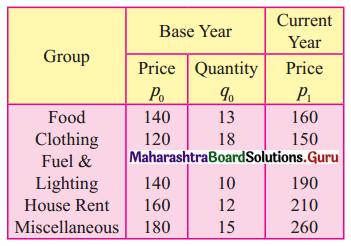
Solution:

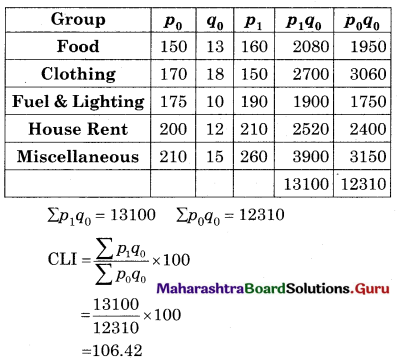
Question 19.
Find the cost living index number by the weighted aggregate method.

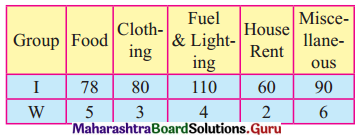
Solution:

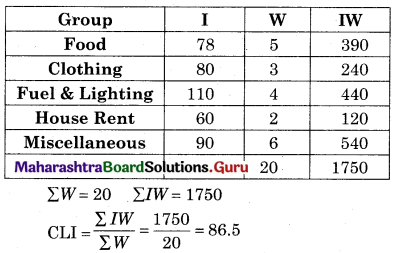
Question 20.
Find the cost of living index number by Family Budget Method for the following data. Also, find the expenditure of a person in the year 2008 if his expenditure in the year 2005 was ₹ 10,000.

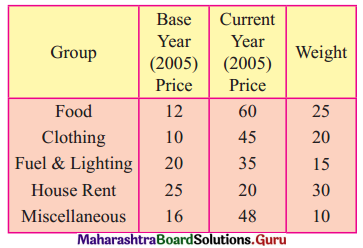
Solution:

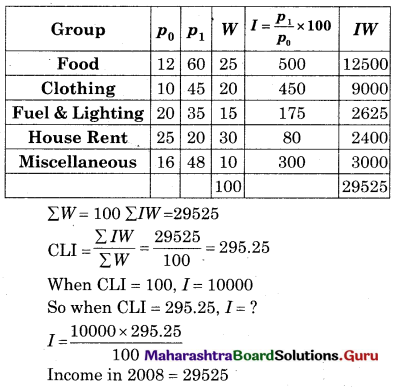
Question 21.
Find x if cost of living index number is 193 for the following data.

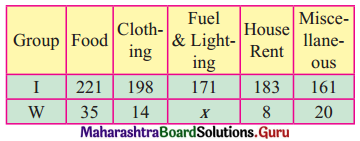
Solution:

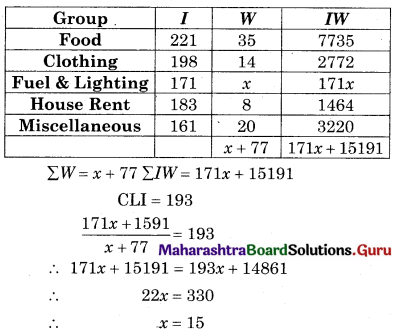
Question 22.
The cost of living number for year 2000 and 2003 are 150 and 210 respectively. A person earns ₹ 13,500 per month in the year 2000. What should be his monthly earning in the year 2003 in order to maintain the same standard of living?
Solution:
CLI (2000) = 150
CLI (2003) = 210
Income (2000) = 13500
Income (2003) = ?
Real Income = \(\frac{\text { Income }}{\mathrm{CLI}} \times 100\)
For 2000, Real Income = \(\frac{13500}{150} \times 100\) = ₹ 9000
For 2003, Real Income = \(\frac{\text { Income }}{\mathrm{CLI}} \times 100\)
∴ 9000 = \(\frac{\text { Income }}{210} \times 100\)
∴ Income = \(\frac{9000 \times 210}{100}\) = 18900
∴ Income in 2003 = ₹ 18900

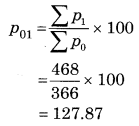
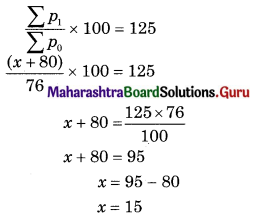
Balbharati Maharashtra State Board 12th Commerce Maths Digest Pdf Chapter 3 Linear Regression Ex 3.2 Questions and Answers.

Maharashtra State Board 12th Commerce Maths Solutions Chapter 3 Linear Regression Ex 3.2

Question 1.
For bivariate data.
\(\bar{x}\) = 53, \(\bar{x}\) = 28, b_yx = -1.2, b_xy = -0.3
Find,
(i) Correlation coefficient between X and Y.
(ii) Estimate Y for X = 50
(iii) Estimate X for Y = 25
Solution:
(i) r² = b_yx . b_xy
r² = (-1.2)(-0.3)
r² = 0.36
r = ±0.6
Since, b_yx and bxy are negative, r = -0.6

(ii) Regression equation of Y on X is
(Y – \(\bar{y}\)) = b_yx (X – \(\bar{x}\))
Y – 28 = -1.2(50 – 53)
Y – 28 = -1.2(-3)
Y – 28 = 3.6
Y = 31.6

(iii) Regression equation of X on Y is
(X – \(\bar{x}\)) = b_xy (Y – \(\bar{y}\))
(X – 53) = -0.3(25 – 28)
X – 53 = -0.3(-3)
X – 53 = 0.9
X = 53.9

Question 2.
From the data of 20 pairs of observation on X and Y, following result are obtained \(\bar{x}\) = 199, \(\bar{y}\) = 94, \(\sum\left(x_{i}-\bar{x}\right)^{2}\) = 1200, \(\sum\left(y_{i}-\bar{y}\right)^{2}\) = 300
\(\sum\left(x_{i}-\bar{x}\right)\left(y_{i}-\bar{y}\right)\) = -250
Find
(i) The line of regression of Y on X.
(ii) The line of regression of X on Y.
(iii) Correlation coefficient between X on Y.
Solution:

Question 3.
From the data of 7 pairs of observations on X and Y following results are obtained.
Σ(x_i – 70 ) = -35, Σ(y_i – 60) = -7, Σ(x_i – 70)² = 2989, Σ(y_i – 60)² = 476, Σ(x_i – 70) (y_i – 60) = 1064 [Given √0.7884 = 0.8879]
Obtain
(i) The line of regression of Y on X.
(ii) The line of regression of X on Y.
(iii) The correlation coefficient between X and Y.
Solution:


(i) Line of regression Y on X is
(Y – \(\bar{y}\)) = b_yx (X – \(\bar{x}\))
(Y – 59) = 0.36(x – 65)
(Y – 59) = 0.36x – 23.4
Y = 0.36x + 35.6

(ii) Line of regression X on Y is
(X – \(\bar{x}\)) = b_xy (Y – \(\bar{y}\))
(X – 65) = 2.19(y – 59)
(X – 65) = 2.19y – 129.21
X = 2.19y – 64.21

(iii) r² = b_yx . b_xy
r² = (0.36) (2.19)
r² = 0.7884
r = ±√0.7884 = ±0.8879
Since b_yx and b_xy are positive.
∴ r = 0.8879

Question 4.
You are given the following information about advertising expenditure and sales.

Correlation coefficient between X and Y is 0.8
(i) Obtain two regression equations.
(ii) What is the likely sales when the advertising budget is ₹ 15 lakh?
(iii) What should be the advertising budget if the company wants to attain sales target of ₹ 120 lakh?
Solution:
Given, \(\bar{x}\) = 10, \(\bar{y}\) = 90, σ_x = 3, σ_y = 12, r = 0.8
byx = \(\frac{r \sigma_{y}}{\sigma_{x}}=0.8 \times \frac{12}{3}\) = 3.2
bxy = \(\frac{r \sigma_{x}}{\sigma_{y}}=0.8 \times \frac{3}{12}\) = 0.2
(i) Regression equation of Y on X is
(Y – \(\bar{y}\)) = b_yx (X – \(\bar{x}\))
(Y – 90) = 3.2(x – 10)
Y – 90 = 3.2x – 32
Y = 3.2x + 58
Regression equation of X on Y is
(X – \(\bar{x}\)) = b_xy (Y – \(\bar{y}\))
(X – 10) = 0.2(y – 90)
X – 10 = 0.2y + 18
X = 0.2y – 8

(ii) When x = 15,
Y = 3.2(15) + 58
= 48 + 58
= 106 lakh

(iii) When y = 120
X = 0.2(120) – 8
= 24 – 8
= 16 lakh

Question 5.
Bring out inconsistency if any, in the following:
(i) b_yx + b_xy = 1.30 and r = 0.75
(ii) b_yx = b_xy = 1.50 and r = -0.9
(iii) b_yx = 1.9 and b_xy = -0.25
(iv) b_yx = 2.6 and b_xy = \(\frac{1}{2.6}\)
Solution:
(i) Given, b_yx + b_xy = 1.30 and r = 0.75
\(\frac{b_{y x}+b_{x y}}{2}=\frac{1.30}{2}\) = 0.65
But for regression coefficients b_yx and b_xy
\(\left|\frac{b_{y x}+b_{x y}}{2}\right| \geq r\)
Here, 0.65 < r = 0.75
∴ The data is inconsistent
(ii) The signs of b_yx, b_xy and r must be same (all three positive or all three negative)
∴ The data is inconsistent.

(iii) The signs of b_yx and b_xy should be same (either both positive or both negative)
∴ The data is consistent.

(iv) b_yx . b_xy = 2.6 × \(\frac{1}{2.6}\) = 1
∴ 0 ≤ r² ≤ 1
∴ The data is consistent.

Question 6.
Two sample from bivariate populations have 15 observation each. The sample means of X and Y are 25 and 18 respectively. The corresponding sum of square of deviations from respective means are 136 and 150. The sum of product of deviations from respective means is 123. Obtain the equation of line of regression of X on Y.
Solution:
Given, n = 15, \(\bar{x}\) = 25, \(\bar{y}\) = 18, Σ(x – \(\bar{x}\)) = 136, Σ(y – \(\bar{y}\)) = 150, Σ(x – \(\bar{x}\)) (y – \(\bar{y}\)) = 123
Regression equation of X on Y is (X – \(\bar{x}\)) = bxy (Y – \(\bar{y}\))
(X – 25) = 0.82(y – 18)
(X – 25) = 082y – 14.76
X = 0.82y + 10.24

Question 7.
For a certain bivariate data

And r = 0.5 estimate y when x = 10 and estimate x when y = 16
Solution:
Given, \(\bar{x}\) = 25, \(\bar{y}\) = 20, σ_x = 4, σ_y = 3, r = 0.5
b_yx = \(\frac{r \sigma_{y}}{\sigma_{y}}=0.5 \times \frac{3}{4}\) = 0.375
Regression equation of Y on X is
(Y – \(\bar{y}\)) = b_yx (X – \(\bar{x}\))
(Y – 20) = 0.375(x – 25)
Y – 20 = 0.375x – 9.375
Y = 0.375x + 10.625
When, x = 10
Y = 0.375(10) + 10.625
= 3.75 + 10.625
= 14.375
b_xy = \(\frac{r \sigma_{x}}{\sigma_{y}}=0.5 \times \frac{4}{3}\) = 0.67
Regression equation of X on Y is
(X – \(\bar{x}\)) = b_yx (Y – \(\bar{y}\))
(X – 25) = 0.67(y – 20)
(X – 25) = 0.67y – 13.4
X = 0.67y + 11.6
When, Y = 16
x = 0.67(16) + 11.6
= 10.72 + 11.6
= 22.32

Question 8.
Given the following information about the production and demand of a commodity obtain the two regression lines:

Coefficient of correlation between X and Y is 0.6. Also estimate the problem when demand is 100.
Solution:
Given \(\bar{x}\) = 85, \(\bar{y}\) = 90, σ_x = 5, σ_y = 6 and r = 0.6
bxy = \(\frac{r \sigma_{x}}{\sigma_{y}}=0.6 \times \frac{5}{6}\) = 0.5
byx = \(\frac{r \sigma_{y}}{\sigma_{x}}=0.6 \times \frac{6}{5}\) = 0.72
Regression equation of X on Y is
(X – \(\bar{x}\)) = b_xy (Y – \(\bar{y}\))
(X – 85) = 0.5(y – 90)
(X – 85 ) = 0.5y – 45
X = 0.5y + 40
When y = 100,
x = 0.5 (100) + 40
= 50 + 40
= 90
Regression equation of Y on X is
(Y – \(\bar{y}\)) = b_yx (X – \(\bar{x}\))
(Y – 90) = 0.72(x – 85)
(Y – 90) = 0.72x – 61.2
Y = 0.72x + 28.8

Question 9.
Given the following data, obtain linear regression estimate of X for Y = 10
Solution:
\(\bar{x}\) = 7.6, \(\bar{y}\) = 14.8, σ_x = 3.2, σ_y = 16 and r = 0.7
b_xy = \(\frac{r \sigma_{x}}{\sigma_{y}}=0.7 \times \frac{3.2}{16}\) = 0.14
Regression equation of X on Y is
(X – \(\bar{y}\)) = b_xy (Y – \(\bar{y}\))
(X – 7.6) = 0.14(y – 14.8)
X – 7.6 = 0.14y – 2.072
X = 0.14y + 5.528
When y = 10
x = 0.14(10) + 5.528
= 1.4 + 5.528
= 6.928

Question 10.
An inquiry of 50 families to study the relationship between expenditure on accommodation (₹ x) and expenditure on food and entertainment (₹ y) gave the following result:
Σx = 8500, Σy = 9600, σ_x = 60, σ_y = 20, r = 0.6
Estimate the expenditure on food and entertainment when expenditure on accommodation is ₹ 200
Solution:
n = 50 (given)

Regression equation of Y on X is
Y – \(\bar{y}\) = b_yx (X – \(\bar{x}\))
(Y – 192) = 0.2(200 – 170)
Y – 192 = 0.2(30)
Y = 192 + 6
Y = 198

Question 11.
The following data about the sales and advertisement expenditure of a firms is given below (in ₹ crores)

Also correlation coefficient between X and Y is 0.9
(i) Estimate the likely sales for a proposed advertisement expenditure of ₹ 10 crores.
(ii) What should be the advertisement expenditure if the firm proposes a sales target ₹ 60 crores
Let the sales be X and advertisement expenditure be Y
Solution:
Given, \(\bar{x}\) = 40, \(\bar{y}\) = 6, σ_x = 10, σ_y = 1.5, r = 0.9
b_yx = \(\frac{r \sigma_{y}}{\sigma_{x}}=0.9 \times \frac{1.5}{10}\) = 0.135
b_xy = \(\frac{r \sigma_{x}}{\sigma_{y}}=0.9 \times \frac{10}{1.5}\) = 6
(i) Regression equation of X on Y is
(X – \(\bar{x}\)) = b_xy (Y – \(\bar{y}\))
(X – 40) = 6(y – 6)
X – 40 = 6y – 36
X = 6y + 4
When y = 10
x = 6 (10) + 4
= 60 + 4
= 64 crores

(ii) Regression equation Y on X is
(Y – \(\bar{y}\)) = b_yx (X – \(\bar{x}\))
(Y – 6) = 0.135 (x – 40)
Y – 6 = 0.135x – 5.4
Y = 0.135x + 0.6
When x = 60
Y = 0.135 (60) + 0.6
= 8.1 + 0.6
= 8.7 crores

Question 12.
For certain bivariate data the following information are available

Correlation coefficient between x and y is 0.6, estimate x when y = 15 and estimate y when x = 10.
Solution:
Given, \(\bar{x}\) = 13, \(\bar{y}\) = 17, σ_x = 3, σ_y = 2, r = 0.6
b_yx = \(\frac{r \sigma_{y}}{\sigma_{x}}=0.6 \times \frac{2}{3}\) = 0.4
b_xy = \(\frac{r \sigma_{x}}{\sigma_{y}}=0.6 \times \frac{3}{2}\) = 0.9
Regression equation of Y on X
(Y – \(\bar{y}\)) = b_yx (X – \(\bar{x}\))
Y – 17 = 0.4(x – 13)
Y = 0.4x + 11.8
When x = 10
Y = 0.4(10) + 11.8
= 4 + 11.8
= 15.8
Regression equation of X on Y
(X – \(\bar{x}\)) = b_xy (Y – \(\bar{y}\))
(X – 13) = 0.9(y – 17)
X – 13 = 0.9y – 15.3
X = 0.9y – 2.3
When y = 15
X = 0.9(15) – 2.3
= 13.5 – 2.3
= 11.2

Balbharati Maharashtra State Board Std 12 Commerce Statistics Part 1 Digest Pdf Chapter 5 Integration Ex 5.4 Questions and Answers.

Maharashtra State Board 12th Commerce Maths Solutions Chapter 5 Integration Ex 5.4

Evaluate the following.

Question 1.
\(\int \frac{1}{4 x^{2}-1} d x\)
Solution:

Question 2.
\(\int \frac{1}{x^{2}+4 x-5} d x\)
Solution:

Question 3.
\(\int \frac{1}{4 x^{2}-20 x+17} d x\)
Solution:

Question 4.
\(\int \frac{x}{4 x^{4}-20 x^{2}-3} d x\)
Solution:

Question 5.
\(\int \frac{x^{3}}{16 x^{8}-25} d x\)
Solution:

Question 6.
\(\int \frac{1}{a^{2}-b^{2} x^{2}} d x\)
Solution:

Question 7.
\(\int \frac{1}{7+6 x-x^{2}} d x\)
Solution:

Question 8.
\(\int \frac{1}{\sqrt{3 x^{2}+8}} d x\)
Solution:

Question 9.
\(\int \frac{1}{\sqrt{x^{2}+4 x+29}} d x\)
Solution:

Question 10.
\(\int \frac{1}{\sqrt{3 x^{2}-5}} d x\)
Solution:

Question 11.
\(\int \frac{1}{\sqrt{x^{2}-8 x-20}} d x\)
Solution:

Balbharati Maharashtra State Board Std 12 Commerce Statistics Part 1 Digest Pdf Chapter 5 Integration Ex 5.3 Questions and Answers.

Maharashtra State Board 12th Commerce Maths Solutions Chapter 5 Integration Ex 5.3

Evaluate the following:

Question 1.
\(\int \frac{3 e^{2 t}+5}{4 e^{2 t}-5} d t\)
Solution:
Let I = \(\int \frac{3 e^{2 t}+5}{4 e^{2 t}-5} d t\)
Put, Numerator = A(Denominator) + B[\(\frac{d}{d x}\)(Denominator)]
∴ 3e^2t + 5 = A(4e^2t – 5) + B[\(\frac{d}{d t}\)(4e^2t – 5)]
∴ 3e^2t + 5 = A(4e^2t – 5) + B[4e^2t × 2 – 0]
∴ 3e^2t + 5 = (4A + 8B) e^2t – 5A
Equating the coefficient of e^2t and constant on both sides, we get
4A + 8B = 3
and -5A = 5
∴ A = -1
∴ from (1), 4(-1) + 8B = 3
∴ 8B = 7
∴ B = \(\frac{7}{8}\)

Question 2.
\(\int \frac{20-12 e^{x}}{3 e^{x}-4} d x\)
Solution:
Let I = \(\int \frac{20-12 e^{x}}{3 e^{x}-4} d x\)
Put, Numerator = A (Denominator) + B[\(\frac{d}{d x}\)(Denominator)]
∴ 20 – 12e^x = A(3e^x – 4) + B[\(\frac{d}{d x}\)(3e^x – 4)]
∴ 20 – 12e^x = A(3e^x – 4) + B(3e^x – 0)
∴ 20 – 12e^x = (3A + 3B)e^x – 4A
Equating the coefficient of ex and constant on both sides, we get
3A + 3B = -12 ……(1)
and -4A = 20
∴ A = -5
from (1), 3(-5) + 3B = -12
∴ 3B = 3
∴ B = 1
∴ 20 – 12e^x = -5(3e^x – 4) + (3e^x)

Question 3.
\(\int \frac{3 e^{x}+4}{2 e^{x}-8} d x\)
Solution:
Let I = \(\int \frac{3 e^{x}+4}{2 e^{x}-8} d x\)
Put, Numerator = A (Denominator) + B[\(\frac{d}{d x}\)(Denominator)]
∴ 3e^x + 4 = A(2e^x – 8) + B[\(\frac{d}{d x}\)(2e^x – 8)]
∴ 3e^x + 4 = A(2e^x – 8) + B(2e^x – 0)
∴ 3e^x + 4 = (2A + 2B)e^x – 8A
Equating the coefficient of ex and constant on both sides, we get
2A + 2B = 3 ……..(1)
and -8A = 4
∴ A = \(-\frac{1}{2}\)
∴ from (1), 2(\(-\frac{1}{2}\)) + 2B = 3
∴ 2B = 4
∴ B = 2

Question 4.
\(\int \frac{2 e^{x}+5}{2 e^{x}+1} d x\)
Solution:

Balbharati Maharashtra State Board Std 12 Commerce Statistics Part 1 Digest Pdf Chapter 5 Integration Ex 5.2 Questions and Answers.

Maharashtra State Board 12th Commerce Maths Solutions Chapter 5 Integration Ex 5.2

Evaluate the following.

Question 1.
\(\int x \sqrt{1+x^{2}} d x\)
Solution:

Question 2.
\(\int \frac{x^{3}}{\sqrt{1+x^{4}}} d x\)
Solution:

Question 3.
\(\int\left(e^{x}+e^{-x}\right)^{2}\left(e^{x}-e^{-x}\right) d x\)
Solution:

Question 4.
\(\int \frac{1+x}{x+e^{-x}} d x\)
Solution:

Question 5.
∫(x + 1)(x + 2)⁷(x + 3) dx
Solution:
Let I = ∫(x + 1)(x + 2)⁷(x + 3) dx
= ∫(x + 2)⁷ (x + 1)(x + 3) dx
= ∫(x + 2)⁷ [(x + 2) – 1][(x + 2) + 1] dx
= ∫(x + 2)⁷ [(x + 2)² – 1] dx
= ∫[(x + 2)⁹ – (x + 2 )⁷] dx
= ∫(x + 2 )⁹ dx – ∫(x + 2)⁷ dx
= \(\frac{(x+2)^{10}}{10}\) – \(\frac{(x+2)^{8}}{8}\) + c

Question 6.
\(\int \frac{1}{x \log x} d x\)
Solution:
Put log x = t
∴ \(\frac{1}{x}\) dx = dt
∴ \(\int \frac{d x}{x \cdot \log x}=\int \frac{1}{\log x} \cdot \frac{1}{x} d x\)
= ∫\(\frac{1}{t}\) dt
= log |t| + c
= log|log x| + c.

Question 7.
\(\int \frac{x^{5}}{x^{2}+1} d x\)
Solution:

Question 8.
\(\int \frac{2 x+6}{\sqrt{x^{2}+6 x+3}} d x\)
Solution:

Question 9.
\(\int \frac{1}{\sqrt{x}+x} d x\)
Solution:

Question 10.
\(\int \frac{1}{x\left(x^{6}+1\right)} d x\)
Solution:

Balbharati Maharashtra State Board Std 12 Commerce Statistics Part 1 Digest Pdf Chapter 5 Integration Ex 5.1 Questions and Answers.

Maharashtra State Board 12th Commerce Maths Solutions Chapter 5 Integration Ex 5.1

Question 1.
Evaluate \(\int \frac{-2}{\sqrt{5 x-4}-\sqrt{5 x-2}} d x\)
Solution:

Question 2.
Evaluate \(\int\left(1+x+\frac{x^{2}}{2 !}\right) d x\)
Solution:

Question 3.
Evaluate \(\int \frac{3 x^{3}-2 \sqrt{x}}{x} d x\)
Solution:

Question 4.
Evaluate ∫(3x² – 5)² dx
Solution:
∫(3x² – 5)² dx
= ∫(9x⁴ – 30x² + 25) dx
= 9∫x⁴ dx – 30∫x² dx + 25∫1 dx
= 9(\(\frac{x^{5}}{5}\)) – 30(\(\frac{x^{3}}{3}\)) + 25x + c
= \(\frac{9x^{5}}{5}\) – 10x³ + 25x + c.

Question 5.
Evaluate \(\int \frac{1}{x(x-1)} d x\)
Solution:

Question 6.
If f'(x) = x² + 5 and f(0) = -1, then find the value of f(x).
Solution:
By the definition of integral
f(x) = ∫f'(x) dx
= ∫(x² + 5) dx
= ∫x² dx + 5∫1 dx
= \(\frac{x^{3}}{3}\) + 5x + c
Now, f(0) = -1 gives
f(0) = 0 + 0 + c = -1
∴ c = -1
∴ from (1), f(x) = \(\frac{x^{3}}{3}\) + 5x – 1.

Question 7.
If f(x) = 4x³ – 3x² + 2x + k, f(0) = -1 and f(1) = 4, find f(x).
Solution:
By the definition of integral
f(x) = ∫f'(x) dx
= ∫(4x³ – 3x² + 2x + k) dx
= 4∫x³ dx – 3∫x² dx + 2∫x dx + k∫1 dx
= 4(\(\frac{x^{4}}{4}\)) – 3(\(\frac{x^{3}}{3}\)) + 2(\(\frac{x^{2}}{2}\)) + kx + c
∴ f(x) = x⁴ – x³ + x² + kx + c
Now, f(0) = 1 gives
f(0) = 0 – 0 + 0 + 0 + c = 1
∴ c = 1
∴ from (1), f(x) = x⁴ – x³ + x² + kx + 1
Further f(1) = 4 gives
f(1) = 1 – 1 + 1 + k + 1 = 4
∴ k = 2
∴ from (2), f(x) = x⁴ – x³ + x² + 2x + 1.

Question 8.
If f(x) = \(\frac{x^{2}}{2}\) – kx + 1, f(0) = 2 and f(3) = 5, find f(x).
Solution:
By the definition of integral

Balbharati Maharashtra State Board 12th Commerce Maths Solution Book Pdf Chapter 4 Applications of Derivatives Miscellaneous Exercise 4 Questions and Answers.

Maharashtra State Board 12th Commerce Maths Solutions Chapter 4 Applications of Derivatives Miscellaneous Exercise 4

(I) Choose the correct alternative:

Question 1.
The equation of tangent to the curve y = x² + 4x + 1 at (-1, -2) is
(a) 2x – y = 0
(b) 2x + y – 5 = 0
(c) 2x – y – 1 = 0
(d) x + y – 1 = 0
Answer:
(a) 2x – y = 0

Question 2.
The equation of tangent to the curve x² + y² = 5, where the tangent is parallel to the line 2x – y + 1 = 0 are
(a) 2x – y + 5 = 0; 2x – y – 5 = 0
(b) 2x + y + 5 = 0; 2x + y – 5 = 0
(c) x – 2y + 5 = 0; x – 2y – 5 = 0
(d) x + 2y + 5; x + 2y – 5 = 0
Answer:
(a) 2x – y + 5 = 0; 2x – y – 5 = 0

Question 3.
If the elasticity of demand η = 1, then demand is
(a) constant
(b) inelastic
(c) unitary elastic
(d) elastic
Answer:
(c) unitary elastic

Question 4.
If 0 < η < 1, then the demand is
(a) constant
(b) inelastic
(c) unitary elastic
(d) elastic
Answer:
(b) inelastic

Question 5.
The function f(x) = x³ – 3x² + 3x – 100, x ∈ R is
(a) increasing for all x ∈ R, x ≠ 1
(b) decreasing
(c) neither increasing nor decreasing
(d) decreasing for all x ∈ R, x ≠ 1
Answer:
(a) increasing for all x ∈ R, x ≠ 1

Question 6.
If f(x) = 3x³ – 9x² – 27x + 15, then
(a) f has maximum value 66
(b) f has minimum value 30
(c) f has maxima at x = -1
(d) f has minima at x = -1
Answer:
(c) f has maxima at x = -1

(II) Fill in the blanks:

Question 1.
The slope of tangent at any point (a, b) is called as ___________
Answer:
gradient

Question 2.
If f(x) = x³ – 3x² + 3x – 100, x ∈ R, then f”(x) is ___________
Answer:
6x – 6 = 6(x – 1)

Question 3.
If f(x) = \(\frac{7}{x}\) – 3, x ∈ R, x ≠ 0, then f”(x) is ___________
Answer:
14x^-3

Question 4.
A rod of 108 m in length is bent to form a rectangle. If area j at the rectangle is maximum, then its dimensions are ___________
Answer:
27 and 27

Question 5.
If f(x) = x . log x, then its maximum value is ___________
Answer:
\(-\frac{1}{e}\)

(III) State whether each of the following is True or False:

Question 1.
The equation of tangent to the curve y = 4xe^x at (-1, \(\frac{-4}{e}\)) is y.e + 4 = 0.
Answer:
True

Question 2.
x + 10y + 21 = 0 is the equation of normal to the curve y = 3x² + 4x – 5 at (1, 2).
Answer:
False

Question 3.
An absolute maximum must occur at a critical point or at an endpoint.
Answer:
True

Question 4.
The function f(x) = x.e^x(1-x) is increasing on (\(\frac{-1}{2}\), 1).
Answer:
True.
Hint:


Hence, function f(x) is increasing on (\(\frac{-1}{2}\), 1).

(IV) Solve the following:

Question 1.
Find the equations of tangent and normal to the following curves:
(i) xy = c² at (ct, \(\frac{c}{t}\)), where t is a parameter.
Solution:
xy = c²
Differentiating both sides w.r.t. x, we get


Hence, equations of tangent and normal are x + t²y – 2ct = 0 and t³x – ty – c(t⁴ + 1) = 0 respectively.

(ii) y = x² + 4x at the point whose ordinate is -3.
Solution:
Let P(x₁, y₁) be the point on the curve
y = x² + 4x, where y₁ = -3



Hence, the equations of tangent and normal at
(i) (-3, -3) are 2x + y + 9 = 0 and x – 2y – 3 = 0
(ii) (-1, -3) are 2x – y – 1 = 0 and x + 2y + 7 = 0

(iii) x = \(\frac{1}{t}\), y = t – \(\frac{1}{t}\), at t = 2.
Solution:
When t = 2, x = \(\frac{1}{2}\) and y = 2 – \(\frac{1}{2}\) = \(\frac{3}{2}\)
Hence, the point P at which we want to find the equations of tangent and normal is (\(\frac{1}{2}\), \(\frac{3}{2}\))



Hence, the equations of tangent and normal are 5x + y – 4 = 0 and x – 5y + 7 = 0 respectively.

(iv) y = x³ – x² – 1 at the point whose abscissa is -2.
Solution:
y = x³ – x² – 1
∴ \(\frac{d y}{d x}=\frac{d}{d x}\)(x³ – x² – 1)
= 3x² – 2x – 0
= 3x² – 2x
∴ \(\left(\frac{d y}{d x}\right)_{\text {at } x=-2}\) = 3(-2)² – 2(-2) = 16
= slope of the tangent at x = -2
When x = -2, y = (-2)³ – (-2)² – 1 = -13
∴ the point P is (-2, -13)
∴ the equation of the tangent at (-2, -13) is
y – (-13) = 16[x – (-2)]
∴ y + 13 = 16x + 32
∴ 16x – y + 19 = 0
The slope of the normal at x = -2
= \(\frac{-1}{\left(\frac{d y}{d x}\right)_{\text {at } x=-2}}=\frac{-1}{16}\)
∴ the equation of the normal at (-2, -13) is
y – (-13) = \(-\frac{1}{16}\)[x – (-2)]
∴ 16y + 208 = -x – 2
∴ x + 16y + 210 = 0
Hence, equations of tangent and normal are 16x – y + 19 = 0 and x + 16y + 210 = 0 respectively.

Question 2.
Find the equation of the normal to the curve y = \(\sqrt{x-3}\) which is perpendicular to the line 6x + 3y – 4 = 0.
Solution:
Let P(x₁, y₁) be the foot of the required normal to the curve y = \(\sqrt{x-3}\)
Differentiating y = \(\sqrt{x-3}\) w.r.t. x, we get



∴ x – 2y – \(\frac{57}{16}\) = 0
i.e. 16x – 32y – 57 = 0
Hence, the equation of the normals are 16x – 32y – 41 = 0 and 16x – 32y – 57 = 0.

Question 3.
Show that the function f(x) = \(\frac{x-2}{x+1}\), x ≠ -1 is increasing.
Solution:
f(x) = \(\frac{x-2}{x+1}\)

∴ f'(x) > 0, for all x ∈ R, x ≠ -1
Hence, the function f is increasing for all x ∈ R, where x ≠ -1.

Question 4.
Show that the function f(x) = \(\frac{3}{x}\) + 10, x ≠ 0 is decreasing.
Solution:
f(x) = \(\frac{3}{x}\) + 10

∴ f'(x) < 0 for all x ∈ R, x ≠ 0
Hence, the function f is decreasing for all x ∈ R, where x ≠ 0.

Question 5.
If x + y = 3, show that the maximum value of x²y is 4.
Solution:
x + y = 3
∴ y = 3 – x
∴ x²y = x²(3 – x) = 3x² – x³
Let f(x) = 3x² – x³
Then f'(x) = \(\frac{d}{d x}\)(3x² – x³)
= 3 × 2x – 3x²
= 6x – 3x²
and f”(x) = \(\frac{d}{d x}\)(6x – 3x²)
= 6 × 1 – 3 × 2x
= 6 – 6x
Now, f'(x) = 0 gives 6x – 3x² = 0
∴ 3x(2 – x) = 0
∴ x = 0 or x = 2
f”(0) = 6 – 0 = 6 > 0
∴ f has minimum value at x = 0
Also, f”(2) = 6 – 12 = -6 < 0
∴ f has maximum value at x = 2
When x = 2, y = 3 – 2 = 1
∴ maximum value of x²y = (2)²(1) = 4.

Question 6.
Examine the function f for maxima and minima, where f(x) = x³ – 9x² + 24x.
Solution:
f(x) = x³ – 9x² + 24x
∴ f'(x) = \(\frac{d}{d x}\)(x³ – 9x² + 24x)
= 3x² – 9 × 2x + 24 × 1
= 3x² – 18x + 24
and f”(x) = \(\frac{d}{d x}\)(3x² – 18x + 24)
= 3 × 2x – 18 × 1 + 0
= 6x – 18
f'(x) = 0 gives 3x² – 18x + 24 = 0
∴ x² – 6x + 8 = 0
∴ (x – 2)(x – 4) = 0
∴ the roots of f'(x) = 0 are x₁ = 2 and x₂ = 4.
(a) f”(2) = 6(2) – 18 = -6 < 0
∴ by the second derivative test,
f has maximum at x = 2 and maximum value of f at x = 2
f(2) = (2) – 9(2)² + 24(2)
= 8 – 36 + 48
= 20
(b) f”(4) = 6(4) – 18 = 6 > 0
∴ by the second derivative test, f has minimum at x = 4
and minimum value of f at x = 4
f(4) = (4)³ – 9(4)² + 24(4)
= 64 – 144 + 96
= 16.

Balbharati Maharashtra State Board 12th Commerce Maths Solution Book Pdf Chapter 4 Applications of Derivatives Ex 4.4 Questions and Answers.

Maharashtra State Board 12th Commerce Maths Solutions Chapter 4 Applications of Derivatives Ex 4.4

Question 1.
The demand function of a commodity at price P is given as D = 40 – \(\frac{5 P}{8}\). Check whether it is increasing or decreasing function.
Solution:
D = 40 – \(\frac{5 P}{8}\)
∴ \(\frac{d D}{d P}=\frac{d}{d P}\left(40-\frac{5 P}{8}\right)\)
= 0 – \(\frac{5}{8}\) × 1
= \(\frac{-5}{8}\)
Hence, the given function is decreasing function.

Question 2.
The price P for demand D is given as P = 183 + 120D – 3D², find D for which price is increasing.
Solution:
P = 183 + 120D – 3D²
∴ \(\frac{d P}{d D}=\frac{d}{d D}\)(183 + 120D – 3D²)
= 0 + 120 × 1 – 3 × 2D
= 120 – 6D
If price P is increasing, then \(\frac{d P}{d D}\) > 0
∴ 120 – 6D > 0
∴ 120 > 6D
∴ D < 20
Hence, the price is increasing when D < 20.

Question 3.
The total cost function for production of x articles is given as C = 100 + 600x – 3x². Find the values of x for which the total cost is decreasing.
Solution:
The cost function is given as
C = 100 + 600x – 3x²
∴ \(\frac{d C}{d D}=\frac{d}{d D}\)(100 + 600x – 3x²)
= 0 + 600 × 1 – 3 × 2x
= 600 – 6x
If the total cost is decreasing, then \(\frac{d C}{d x}\) < 0
∴ 600 – 6x < 0
∴ 600 < 6x
∴ x > 100
Hence, the total cost is decreasing for x > 100.

Question 4.
The manufacturing company produces x items at the total cost of ₹(180 + 4x). The demand function for this product is P = (240 – x). Find x for which
(i) revenue is increasing
(ii) profit is increasing.
Solution:
(i) Let R be the total revenue.
Then R = P.x = (240 – x)x
∴ R = 240x – x²
∴ \(\frac{d R}{d D}=\frac{d}{d D}\)(240x – x²)
= 240 × 1 – 2x
= 240 – 2x
R is increasing, if \(\frac{d R}{d x}\) > 0
i.e. if 240 – 2x > 0
i.e. if 240 > 2x
i.e. if x < 120
Hence, the revenue is increasing, if x < 120.

(ii) Profit π = R – C
∴ π = (240x – x²) – (180 + 4x)
= 240x – x² – 180 – 4x
= 236x – x² – 180
∴ \(\frac{d \pi}{d x}=\frac{d}{d x}\)(236x – x² – 180)
= 236 × 1 – 2x – 0
= 236 – 2x
Profit is increasing, if \(\frac{d \pi}{d x}\) > 0
i.e. if 236 – 2x > 0
i.e. if 236 > 2x
i.e. if x < 118
Hence, the profit is increasing, if x < 118.

Question 5.
For manufacturing x units, labour cost is 150 – 54x and processing cost is x². Price of each unit is p = 10800 – 4x². Find the values of x for which
(i) total cost is decreasing
(ii) revenue is increasing.
Solution:
(i) Total cost C = labour cost + processing cost
∴ C = 150 – 54x + x²
∴ \(\frac{d C}{d x}=\frac{d}{d x}\)(150 – 54x + x²)
= 0 – 54 × 1 + 2x
= -54 + 2x
The total cost is decreasing, if \(\frac{d C}{d x}\) < 0
i.e. if -54 + 2x < 0
i.e. if 2x < 54
i.e. if x < 27
Hence, the total cost is decreasing, if x < 27.

(ii) The total revenue R is given as
R = p.x
R = (10800 – 4x²) x
R = 10800x – 4x³
∴ \(\frac{d R}{d x}=\frac{d}{d x}\)(10800x – 4x³)
= 10800 × 1 – 4 × 3x²
= 10800 – 12x²
The revenue is increasing, if \(\frac{d R}{d x}\) > 0
i.e. if 10800 – 12x² > 0
i.e. if 10800 > 12x²
i.e. if x² < 900
i.e. if x < 30 ……[∵ x > 0]
Hence, the revenue is increasing, if x < 30.

Question 6.
The total cost of manufacturing x articles is C = 47x + 300x² – x⁴. Find x, for which average cost is
(i) increasing
(ii) decreasing.
Solution:
The total cost is given as C = 47x + 300x² – x⁴
∴ the average cost is given by

(i) CA is increasing, if \(\frac{d C_{A}}{d x}\) > 0
i.e. if 300 – 3x² > 0
i.e. if 300 > 3x²
i.e. if x² < 100
i.e. if x < 10 …..[∵ x > 0]
Hence, the average cost is increasing, if x < 10.

(ii) CA is decreasing, if \(\frac{d C_{A}}{d x}\) < 0
i.e. if 300 – 3x² < 0
i.e. if 300 < 3x²
i.e. if x² > 100
i.e. if x > 10 ……[∵ x > 0]
Hence, the average cost is decreasing, if x > 10.

Question 7.
(i) Find the marginal revenue, if the average revenue is 45 and the elasticity of demand is 5.
Solution:
Given R_A = 45 and η = 5
Now, R_m = \(R_{A}\left(1-\frac{1}{\eta}\right)\)
= 45(1 – \(\frac{1}{5}\))
= 45(\(\frac{4}{5}\))
= 36
Hence, the marginal revenue = 36.

(ii) Find the price, if the marginal revenue is 28 and elasticity of demand is 3.
Solution:
Given R_m = 28 and η = 3

Hence, the price = 42.

(iii) Find the elasticity of demand, if the marginal revenue is 50 and price is ₹ 75.
Solution:
Given R_m = 50 and R_A = 75

Hence, the elasticity of demand = 3.

Question 8.
If the demand function is D = \(\frac{p+6}{p-3}\), find the elasticity of demand at p = 4.
Solution:
The demand function is

Elasticity of demand is given by

Hence, the elasticity of demand at p = 4 is 3.6

Question 9.
Find the price for the demand function D = \(\frac{2 p+3}{3 p-1}\), when elasticity of demand is \(\frac{11}{14}\).
Solution:
The demand function is

Elasticity of demand is given by

Question 10.
If the demand function is D = 50 – 3p – p² elasticity of demand at (i) p = 5 (ii) p = 2. Comment on the result.
Solution:
The demand function is D = 50 – 3p – p²
∴ \(\frac{d D}{d p}=\frac{d}{d p}\)(50 – 3p – p²)
= 0 – 3 × 1 – 2p
= -3 – 2p
Elasticity of demand is given by

(i) When p = 5, then

Since, η >1, the demand is elastic.
(ii) When p = 2, then

Since, 0 < η < 1, the demand is inelastic.

Question 11.
For the demand function D = 100 – \(\frac{p^{2}}{2}\), find the elasticity of demand at (i) p = 10 (ii) p = 6 and comment on the results.
Solution:
The demand function is

The elasticity of demand is given by

(i) When p = 10, then

Since, η > 1, the demand is elastic.
(ii) When p = 6, then

Since, 0 < η < 1, the demand is inelastic.

Question 12.
A manufacturing company produces, x items at a total cost of ₹(40 + 2x). Their price is given as p = 120 – x. Find the value of x for which
(i) revenue is increasing
(ii) profit is increasing
(iii) Also find an elasticity of demand for price 80.
Solution:
(i) The total revenue R is given by
R = p.x = (120 – x)x
∴ R = 120x – x²
∴ \(\frac{d R}{d x}=\frac{d}{d x}\)(120x – x²)
= 120 × 1 – 2x
= 120 – 2x
If the revenue is increasing, then \(\frac{d R}{d x}\) > 0
∴ 120 – 2x > 0
∴ 120 > 2x
∴ x < 60
Hence, the revenue is increasing when x < 60.

(ii) Profit π = R – C
= (120x – x²) – (40 + 2x)
= 120x – x² – 40 – 2x
= 118x – x² – 40
∴ \(\frac{d \pi}{d x}=\frac{d}{d x}\)(118x – x² – 40)
= 118 × 1 – 2x – 0
= 118 – 2x
If the profit is increasing, then \(\frac{d \pi}{d x}\) > 0
∴ 118 – 2x > 0
∴ 118 > 2x
∴ x < 59
Hence, the profit is increasing when x < 59.

(iii) p = 120 – x
∴ x = 120 – p
∴ \(\frac{d x}{d p}=\frac{d}{d p}\)(120 – p)
= 0 – 1
= -1
Elasticity of demand is given by

Question 13.
Find MPC, MPS, APC and APS, if the expenditure E_c of a person with income I is given as
E_c = (0.0003)I² + (0.075)I, when I = 1000.
Solution:
E_c = (0.0003)I² + (0.075)I
MPC = \(\frac{d E_{c}}{d I}=\frac{d}{d I}\)[(0.0003)I2 + (0.075)I]
= (0.0003)(2I) + (0.075)(1)
= (0.0006)I + 0.075
When I = 1000, then
MPC = (0.0006)(1000) + 0.075
= 0.6 + 0.075
= 0.675.
∴ MPC + MPS = 1
∴ 0.675 + MPS = 1
∴ MPS = 1 – 0.675 = 0.325
Now, APC = \(\frac{E_{c}}{I}=\frac{(0.0003) I^{2}+(0.075) I}{I}\)
= (0.0003)I + (0.075)
When I = 1000, then
APC = (0.0003)(1000) + 0.075
= 0.3 + 0.075
= 0.375
∵ APC + APS = 1
∴ 0.375 + APS = 1
∴ APS = 1 – 0.375 = 0.625
Hence, MPC = 0.675, MPS = 0.325, APC = 0.375, APS = 0.625.