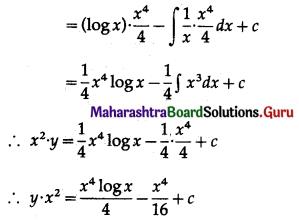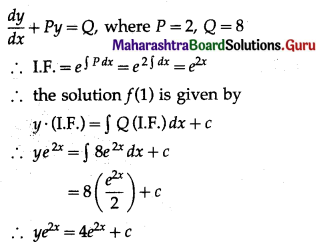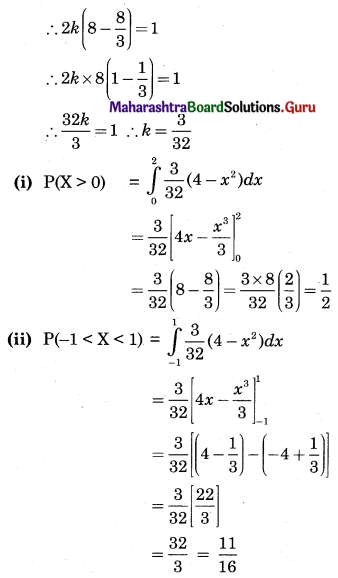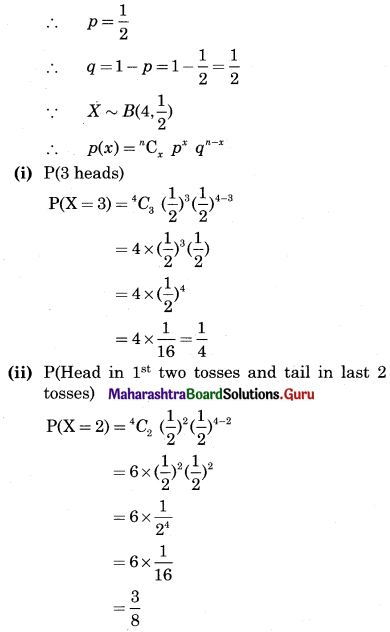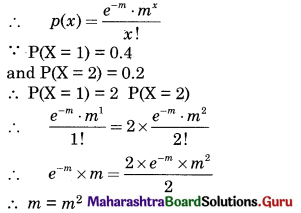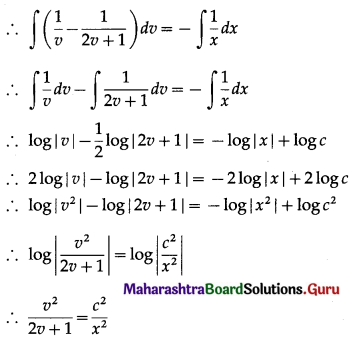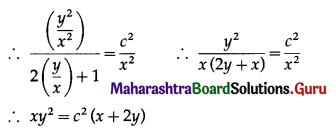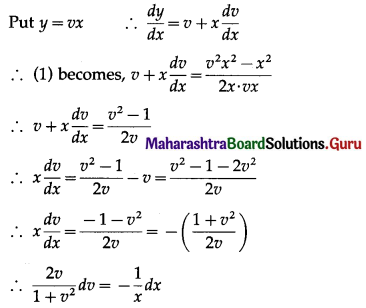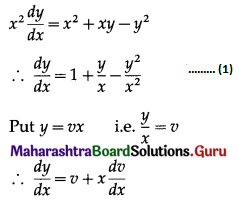Class 12

Balbharati Maharashtra State Board 12th Commerce Maths Digest Pdf Chapter 3 Linear Regression Ex 3.1 Questions and Answers.

Maharashtra State Board 12th Commerce Maths Solutions Chapter 3 Linear Regression Ex 3.1

Question 1.
The HRD manager of the company wants to find a measure which he can use to fix the monthly income of persons applying for the job in the production department. As an experimental project. He collected data of 7 persons from that department referring to years of service and their monthly incomes.

(i) Find the regression equation of income on years of service.
(ii) What initial start would you recommend for a person applying for the job after having served in a similar capacity in another company for 13 years?
Solution:


(i) Regression equation of Y on X is (Y – \(\bar{y}\)) = b_yx (x – \(\bar{x}\))
(Y – 8) = 0.75(x – \(\bar{x}\))
Y = 0.75x + 2
(ii) When x = 13
Y = 0.75(13) + 2 = 11.75
Recommended income for the person is ₹ 11750.

Question 2.
Calculate the regression equations of X on Y and Y on X from the following date:

Solution:


Regression equation of X on Y is (X – \(\bar{x}\)) = b_xy (Y – \(\bar{y}\))
(X – 14) = 1(Y – 8)
X – 14 = Y – 8
X = Y + 6
Regression equation Y on X is (Y – \(\bar{y}\)) = b_yx (X – \(\bar{x}\))
(Y – 8) = 0.87(X – 14)
Y – 8 = 0.87X – 12.18
Y = 0.87X – 4.18

Question 3.
For a certain bivariate data on 5 pairs of observations given
Σx = 20, Σy = 20, Σx² = 90, Σy² = 90, Σxy = 76
Calculate (i) cov(x, y), (ii) b_yx and b_xy, (iii) r
Solution:


Sine byx and bxy are negative, r = -0.4

Question 4.
From the following data estimate y when x = 125

Solution:
Let u = x – 122, v = y – 14

Regression equation of Y on X is
(Y – \(\bar{y}\)) = b_yx (X – \(\bar{x}\))
(Y – 13.5) = -0.21(x – 121.5)
Y – 13.5 = -0.21x + 25.52
Y = -0.21x + 39.02
When x = 125
Y = -0.21(125) + 39.02
= -26.25 + 39.02
= 12.77

Question 5.
The following table gives the aptitude test scores and productivity indices of 10 works selected at workers selected randomly.

Obtain the two regression equation and estimate
(i) The productivity index of a worker whose test score is 95.
(ii) The test score when productivity index is 75.
Solution:


Regression equation of Y on X,
(Y – \(\bar{y}\)) = b_yx (X – \(\bar{y}\))
(Y – 65) = 1.16 (x – 65)
Y – 65 = 1.16x – 75.4
Y = 1.16x – 10.4
(i) When x = 95
Y = 1.16(95) – 10.4
= 110.2 – 10.4
= 99.8
Regression equation of X on Y,
(X – \(\bar{x}\)) = b_xy (Y – \(\bar{y}\))
(X – 65) = 0.59(y – 65)
(X – 65) = 0.59y – 38.35
X = 0.59y + 26.65
(ii) When y = 75
x = 0.59(75) + 26.65
= 44.25 + 26.65
= 70.9

Question 6.
Compute the appropriate regression equation for the following data.

Solution:
Since x is the independent variable, and y is the dependent variable,
we need to find regression equation of y on x


Regression equation of y on x is (y – \(\bar{y}\)) = b_yx (x – \(\bar{x}\))
(y – 10) = -13.4(x – 6)
y – 10 = -1.34x + 8.04
y = -1.34x + 18.04

Question 7.
The following are the marks obtained by the students in Economic (X) and Mathematics (Y)

Find the regression equation of Y and X.
Solution:
Let u = x – 61, v = y – 80

Regression equation of Y on X is
(Y – \(\bar{y}\)) = b_yx (X – \(\bar{x}\))
(Y – 80.4) = 0.3(x – 61)
Y – 80.4 = 0.3x – 18.3
Y = 0.3x + 62.1

Question 8.
For the following bivariate data obtain the equation of two regressions lines:

Solution:


Regression equation of Y on X
(Y – \(\bar{y}\)) = b_yx (X – \(\bar{x}\))
(Y – 9) = 2(x – 3)
Y – 9 = 2x – 6
Y = 2x + 3
Regression equation of X on Y
(X – \(\bar{x}\)) = b_xy (Y – \(\bar{y}\))
(X – 3) = 0.5(y – 9)
(X – 3) = 0.5y – 4.5
X = 0.5y – 1.5

Question 9.
Find the following data obtain the equation of two regression lines:

Solution:


Regression of Y on X,
(Y – \(\bar{y}\)) = b_yx (X – \(\bar{x}\))
(Y – 8) = 0.65(x – 6)
Y – 8 = -0.65x + 3.9
Y = -0.65x + 11.9
Regression of X on Y
(X – \(\bar{x}\)) = b_xy (Y – \(\bar{y}\))
(X – 6) = -1.3(y – 8)
(X – 6) = -1.3y + 10.4
X = -1.3y + 16.4

Question 10.
For the following data, find the regression line of Y on X

Hence find the most likely value of y when x = 4
Solution:

(Y – 3) = 2(x – 2)
Y – 3 = 2x – 4
Y = 2x – 1
When x = 4
Y = 2(4) – 1
= 8 – 1
= 7

Question 11.
Find the following data, find the regression equation of Y on X, and estimate Y when X = 10.

Solution:

Regression equation of Y on X is
(Y – \(\bar{y}\)) = b_yx (X – \(\bar{x}\))
(Y – 5) = (0.63)(x – 3.5)
Y – 5 = 0.63x – 2.2
Y = 0.63x + 2.8
When x = 10
Y = 0.63(10) + 2.8
= 6.3 + 2.8
= 9.1

Question 12.
The following sample gave the number of hours of study (X) per day for an examination and marks (Y) obtained by 12 students.

Obtain the line of regression of marks on hours of study.
Solution:
Let u = x – 5, v = y – 70

∴ Equation of marks on hours of study is
(Y – \(\bar{y}\)) = b_yx (X – \(\bar{x}\))
(Y – 70.83) = 6.6(x – 4.92)
Y – 70.83 = 6.6x – 32.47
∴ Y = 6.6x + 38.36

Balbharati Maharashtra State Board 12th Commerce Maths Digest Pdf Chapter 4 Time Series Miscellaneous Exercise 4 Questions and Answers.

Maharashtra State Board 12th Commerce Maths Solutions Chapter 4 Time Series Miscellaneous Exercise 4

(I) Choose the correct alternative.

Question 1.
Which of the following can’t be a component of a time series?
(a) Seasonality
(b) Cyclical
(c) Trend
(d) Mean
Answer:
(d) Mean

Question 2.
The first step in time series analysis is to
(a) Perform regression calculations
(b) Calculate a moving average
(c) Plot the data on a graph
(d) Identify seasonal variation
Answer:
(c) Plot the data on a graph

Question 3.
Time-series analysis is based on the assumption that
(a) Random error terms are normally distributed.
(b) The variable to be forecast and other independent variable are correlated.
(c) Past patterns in the variable to be forecast will continue unchanged into the future.
(d) The data do not exhibit a trend.
Answer:
(c) Past patterns in the variable to be forecast will continue unchanged into the future.

Question 4.
Moving averages are useful in identifying
(a) Seasonal component
(b) Irregular component
(c) Trend component
(d) Cyclical component
Answer:
(c) Trend component

Question 5.
We can use regression line for past data to forecast future data. We then use the line which
(a) Minimizes the sum of squared deviations of past data from the line.
(b) Minimizes the sum of deviations of past data from the line.
(c) Maximizes the sum of squared deviations of past data from the line.
(d) Maximizes the sum of deviation of past data from the line.
Answer:
(a) Minimizes the sum of squared deviations of past data from the line

Question 6.
Which of the following is a major problem for forecasting, especially when using the method of least squares?
(a) The past cannot be known
(b) The future is not entirely certain
(c) The future exactly follows the patterns of the past
(d) The future may not follow the patterns of the past
Answer:
(d) The future may not follow the patterns of the past

Question 7.
An overall upward or downward pattern in an annual time series would be contained in which component of the time series
(a) Trend
(b) Cyclical
(c) Irregular
(d) Seasonal
Answer:
(a) Trend

Question 8.
The following trend line equation was developed for annual sales from 1984 to 1990 with 1984 as base or zero year. Y1 = 500 + 60X (in 1000 Rs.) The estimated sales for 1984 (in 1000 Rs) is:
(a) ₹ 500
(b) ₹ 560
(c) ₹ 1,040
(d) ₹ 1100
Answer:
(a) ₹ 500

Question 9.
What is a disadvantage of the graphical method of determining a trend line?
(a) Provides quick approximations
(b) Is subject to human error
(c) Provides accurate forecasts
(d) Is too difficult to calculate
Answer:
(b) Is subject to human error

Question 10.
Which component of time series refers to erratic time series movements that follow no recognizable or regular pattern.
(a) Trend
(b) Seasonal
(c) Cyclical
(d) Irregular
Answer:
(a) Trend

(II) Fill in the blanks.

Question 1.
_________ components of time series is indicated by a smooth line.
Answer:
Trend

Question 2.
_________ component of time series is indicated by periodic variation year after year.
Answer:
Seasonal

Question 3.
_________ component of time series is indicated by a long wave spanning two or more years.
Answer:
Cyclical

Question 4.
_________ component of time series is indicated by up and down movements without any pattern.
Answer:
Irregular

Question 5.
Addictive models of time series _________ independence of its components.
Answer:
assume

Question 6.
Multiplicative models of time series _________ independence of its components.
Answer:
does not assume

Question 7.
The simplest method of measuring the trend of time series is _________
Answer:
graphical method

Question 8.
The method of measuring the trend of time series using only averages is _________
Answer:
moving average method

Question 9.
The complicated but ancient method of measuring the trend of time series is _________
Answer:
least-squares method

Question 10.
The graph of time series clearly shows _________ of it is monotone.
Answer:
trend

(III) State whether each of the following is True or False.

Question 1.
The secular trend component of the time series represents irregular variations.
Answer:
False

Question 2.
Seasonal variation can be observed over several years.
Answer:
True

Question 3.
Cyclical variation can occur several times in a year.
Answer:
False

Question 4.
Irregular variation is not a random component of time series.
Answer:
False

Question 5.
The additive model of time series does not require the assumptions of independence of its components.
Answer:
False

Question 6.
The multiplicative model of time series does not require the assumption of independence of its components.
Answer:
True

Question 7.
The graphical method of finding trends is very complicated and involves several calculations.
Answer:
False

Question 8.
Moving the average method of finding trends is very complicated and involves several calculations.
Answer:
False

Question 9.
The least-squares method of finding trends is very simple and does not involve any calculations.
Answer:
False

Question 10.
All three methods of measuring trends will always give the same results.
Answer:
False

(IV) Solve the following problems.

Question 1.
The following table shows the productivity of pig-iron and ferro-alloys (‘000 metric tonnes)

Fit a trend line to the above data by graphical method.
Solution:

Question 2.
Fit a trend line to the data in Problem IV (1) by the method of least squares.
Solution:

u = \(\frac{t-1978}{1}\), Σy = 57, Σu = 0, Σu² = 60, Σuy = 38, n = 9
Let the equation of the trend line be
Y = a + bu where u = t – 1978 ……(i)
Σy = na + bΣu ………(ii)
Σuy = aΣu + bΣu² ………(iii)
Substituting the values of Σu, n, Σuy, Σu² in (ii) & (iii) we get
57 = 9a + 0 ∴ a = 6.3333
38 = 0 + b . 60 ∴ b = 0.6333.
∴ The equation of the trend line is
y = 6.3333 + 0.63333u where u = t – 1978

Question 3.
Obtain the trends values for the data on problem IV (1) using 5 yearly moving averages.
Solution:

Question 4.
The following table shows the amount of sugar production (in lac tonnes) for the years 1971 to 1982.

Fit a trend line to the above data by graphical method.
Solution:

Question 5.
Fit a trend line to data in problem 4 by the method of least squares.
Solution:

u = \(\frac{t-1976.5}{\frac{1}{2}}\), Σy = 38, Σu = 0, Σu² = 572, Σuy = 160, n = 12
Let the equation of the trend line be
y = a + bu ……..(i)
where u = \(\frac{t-1976.5}{\frac{1}{2}}\)
u = 2t – 3953
Σy = na + bΣu ………(ii)
Σuy = aΣu + bΣu² ……..(iii)
by (ii) 38 = 12o + 0 ∴ a = 3.1867
by (iii) 160 = 0 + b . 572 ∴ b = 0.2797
∴ by (i), Equation of the trend line is
Y = 3.1667 + 0.2797u where u = 2t – 3953.

Question 6.
Obtain trend values for data in Problem 4 using 4-yearly centered moving averages.
Solution:

Question 7.
The percentage of girls’ enrollment in total enrollment for years 1960-2005 is shown in the following table.

Fit a trend line to the above data by graphical method.
Solution:

Question 8.
Fit a trend line to the data in Problem 7 by the method of least squares.
Solution:

u = \(\frac{t-1980.5}{5}\), Σy = 51, Σu = 0, Σu² = 330, Σuy = 157, n = 10
Let the equation of the trend line be
Y = a + bu where u = \(\frac{t-1980.5}{5}\) …….(i)
Σy = na + bΣu ……..(ii)
Σuy = aΣu + bΣu² ……..(iii)
Substituting the values of Σy, Σu, n, Σuy, Σu² We get
51 = 10a + 0 ∴ a = 5.1
and 157 = 0 + 6.330 ∴ b = 0.4758
by (i) equation of the trend line is
Y = 5.1 + 0.4758u where u = \(\frac{t-1980.5}{5}\)

Question 9.
Obtain trend values for the data in Problem 7 using 4-yearly moving averages.
Solution:

Question 10.
The following data shows the number of boxes of cereal sold in the years 1977 to 1984.

Fit a trend line to the above data by graphical method.
Solution:

Question 11.
Fit a trend line to data in Problem 10 by the method of least squares.
Solution:

u = \(\frac{t-1980.5}{\frac{1}{2}}\), Σy = 39, Σu = 0, Σu² = 168, Σuy = 79, n = 8
Let the equation of the trend line by
Y = a + bu
Where u = 2t – 3961 …….(i)
Σy = na + bΣu …….(ii)
Σuy = aΣu + bΣu² ……..(iii)
Substituting the values of Σy, n, Σu, Σuy, Σu², in (ii) & (iii)
39 = 8a + 0 ∴ a = 4.875
79 = 0 + b (168) ∴ b = 0.4702
by (i) the equation of the trend line is
Y = 4.875 + 0.4702u Where u = 2t – 3961.

Question 12.
Obtain trend values for data in Problem 10 using 3-yearly moving averages.
Solution:

Question 13.
The following table shows the number of trade fatalities (in a state) resulting from drunken driving for the years 1975 to 1983.

Fit a trend line to the above data by graphical method.
Solution:

Question 14.
Fit a trend line to data in Problem 13 by the method of least squares.
Solution:

u = \(\frac{t-1979}{1}\), Σy = 47, Σu = 0, Σu² = 60, Σuy = 40, n = 9
Let the equation of the trends line be
Y = a + bu where u = t – 1979 …….(i)
Σy = na + bΣu ………(ii)
Σuy = aΣu + bΣu² ……..(iii)
Substituting values of Σy, n, Σu, Σuy, Σu² in (ii) & (iii)
We get 47 = 9a + 0 ∴ a = 5.2222
and 40 = 0 + b(60) ∴ b = 0.6667
∴ by (i) the equation of the trend line is
Y = 5.2222 + 0.6667u Where u = t – 1979.

Question 15.
Obtain trend values for data in Problem 13 using 4-yearly moving averages.
Solution:

Question 16.
The following table shows the all India infant mortality rates (per ‘000) for the years 1980 to 2000.

Fit a trend line to the above data by graphical method.
Solution:

Question 17.
Fit a trend line to data in Problem 16 by the method of least squares.
Solution:

u = \(\frac{t-1995}{5}\), Σy = 30, Σu = 0, Σu² = 70, Σuy = -70, n = 7
Let the equation of the trend line be
Y = a + bu Where u = \(\frac{t-1995}{5}\) …..(i)
Σy = na + bΣu ……(ii)
Σuy = aΣu + bΣu² …….(iii)
Substituting values of Σy, n, Σu, Σuy & Σu² in (ii) & (iii) we get
30 = 7a + 0 ∴ a = 4.2857
-70 = 0 + 6(70) ∴ b = -1
∴ by (i) the equation of the trend line is
y = 4.2857 – 1(u) Where u = \(\frac{t-1995}{5}\)

Question 18.
Obtain trend values for data in Problem 16 using 3-yearly moving averages.
Solution:

Question 19.
the following table shows the wheat yield (‘000 tonnes) in India for the years 1959 to 1968.

Fit a trend line to the above data by the method of least squares.
Solution:

u = \(\frac{t-1963.5}{\frac{1}{2}}\), Σy = 24, Σu = 0, Σu² = 330, Σuy = 94, n = 10
Let the equation of the trend line be
y = a + bu where u = \(\frac{t-1963.5}{\frac{1}{2}}\) ……(i)
i.e. u = 2t – 3927
Σy = na + bΣu …….(ii)
Σuy = aΣu + Σu² …..(iii)
Substituting values of Σy, n, Σu, Σuy & Σu² in (ii) & (iii) we get
24 = 10a + 0 ∴ a = 2.4
94 = 0 + 6.330 ∴ b = 0.2848
∴ Equation of the trend line is
y = 2.4 + (0.2848)u where u = 2t – 3927

Question 20.
Obtain trend values for data in problem 19 using 3-yearly moving averages.
Solution:

Balbharati Maharashtra State Board Std 12 Commerce Statistics Part 1 Digest Pdf Chapter 8 Differential Equation and Applications Ex 8.6 Questions and Answers.

Maharashtra State Board 12th Commerce Maths Solutions Chapter 8 Differential Equation and Applications Ex 8.6

Question 1.
In a certain culture of bacteria, the rate of increase is proportional to the number present. If it is found that the number doubles in 4 hours, find the number of times the bacteria are increased in 12 hours.
Solution:
Let x be the number of bacteria in the culture at time t.
Then the rate of increase is \(\frac{d x}{d t}\) which is proportional to x.
∴ \(\frac{d x}{d t}\) ∝ x
∴ \(\frac{d x}{d t}\) = kx, where k is a constant
∴ \(\frac{d x}{x}\) = k dt
On integrating, we get
∫\(\frac{d x}{x}\) = k∫dt
∴ log x = kt + c
Initially, i.e. when t = 0, let x = x₀
∴ log x₀ = k × 0 + c
∴ c = log x₀
∴ log x = kt + log x₀
∴ log x – log x₀ = kt
∴ log(\(\frac{x}{x_{0}}\)) = kt ……(1)
Since the number doubles in 4 hours, i.e. when t = 4, x = 2x₀

∴ the number of bacteria will be 8 times the original number in 12 hours.

Question 2.
If the population of a town increases at a rate proportional to the population at that time. If the population increases from 40 thousand to 60 thousand in 40 years, what will be the population in another 20 years? (Given: \(\sqrt{\frac{3}{2}}\) = 1.2247)
Solution:
Let P be the population of the city at time t.
Then \(\frac{d P}{d t}\), the rate of increase of population, is proportional to P.
∴ \(\frac{d P}{d t}\) ∝ P
∴ \(\frac{d P}{d t}\) = kP, k is a constant
∴ \(\frac{d P}{P}\) = k dt
Integrating, we get
∫\(\frac{d P}{P}\) = k∫dt
∴ log P = kt + c
Initially, i.e. when t = 0, P = 40000
∴ log 40000 = 0 + c
∴ c = log 40000
∴ log P = kt + log 40000
∴ log P – log 40000 = kt
∴ log(\(\frac{P}{40000}\)) = kt ………(1)
When t = 40, P = 60000

∴ population after 60 years will be 73482.

Question 3.
The rate of growth of bacteria is proportional to the number present. If initially, there were 1000 bacteria and the number doubles in 1 hour, find the number of bacteria after \(\frac{5}{2}\) hours. [Given: √2 = 1.414]
Solution:
Let x be the number of bacteria at time t.
Then the rate of increase is \(\frac{d x}{d t}\) which is proportional to x.
∴ \(\frac{d x}{d t}\) ∝ x
∴ \(\frac{d x}{d t}\) = kx, where k is a constant
∴ \(\frac{d x}{x}\) = k dt
On integrating, we get
∫\(\frac{d x}{x}\) = k∫dt
∴ log x = kt + c
Initially, i.e. when t = 0, x = 1000
∴ log 1000 = k × 0 + c
∴ c = log 1000
∴ log x = kt + log 1000
∴ log x – log 1000 = kt
∴ log(\(\frac{x}{1000}\)) = kt …….(1)
Now, when t = 1, x = 2 × 1000 = 2000

∴ number of bacteria after \(\frac{5}{2}\) hours = 5656.

Question 4.
Find the population of a city at any time t, given that the rate of increase of population is proportional to the population at that instant and that in a period of 40 years, the population increased from 30,000 to 40,000.
Solution:
Let P be the population of the city at time t.
Then \(\frac{d P}{d t}\), the rate of increase of population, is proportional to P.
∴ \(\frac{d P}{d t}\) ∝ P
∴ \(\frac{d P}{d t}\) = kP, where k is a constant.
∴ \(\frac{d P}{P}\) = k dt
On integrating, we get
∫\(\frac{1}{P}\)dP = k∫dt
∴ log P = kt + c
Initially, i.e. when t = 0, P = 30000
∴ log 30000 = k x 0 + c
∴ c = log 30000
∴ log P = kt + log 30000
∴ log P – log 30000 = kt

∴ the population of the city at time t = 30000\(\left(\frac{4}{3}\right)^{\frac{t}{40}}\).

Question 5.
The rate of depreciation \(\frac{d V}{d t}\) of a machine is inversely proportional to the square of t + 1, where V is the value of the machine t years after it was purchased. The initial value of the machine was ₹ 8,00,000 and its value decreased ₹ 1,00,000 in the first year. Find the value after 6 years.
Solution:
Let V be the value of the machine at the end of t years.
Then \(\frac{d V}{d t}\), the rate of depreciation, is inversly proportional to (t + 1)².

Initially, i.e. when t = 0, V = 800000
∴ 800000 = \(\frac{k}{1}\) + c = k + c ………(1)
Now, when t = 1, V = 800000 – 100000 = 700000
∴ 700000 = \(\frac{k}{1+1}\) + c = \(\frac{k}{2}\) + c ……(2)
Subtracting (2) from (1), we get
100000 = \(\frac{1k}{2}\)
∴ k = 200000
∴ from (1), 800000 = 200000 + c
∴ c = 600000 200000
∴ V = \(\frac{200000}{t+1}\) + 600000
When t = 6,
V = \(\frac{200000}{7}\) + 600000
= 28571.43 + 600000
= 628571.43 ~ 628571
Hence, the value of the machine after 6 years will be ₹ 6,28,571.

Balbharati Maharashtra State Board Std 12 Commerce Statistics Part 1 Digest Pdf Chapter 8 Differential Equation and Applications Ex 8.5 Questions and Answers.

Maharashtra State Board 12th Commerce Maths Solutions Chapter 8 Differential Equation and Applications Ex 8.5

Solve the following differential equations.

Question 1.
\(\frac{d y}{d x}+y=e^{-x}\)
Solution:
\(\frac{d y}{d x}+y=e^{-x}\) …….(1)
This is the linear differential equation of the form

This is the general solution.

Question 2.
\(\frac{d y}{d x}\) + y = 3
Solution:
\(\frac{d y}{d x}\) + y = 3
This is the linear differential equation of the form

This is the general solution.

Question 3.
x\(\frac{d y}{d x}\) + 2y = x² . log x.
Solution:
x\(\frac{d y}{d x}\) + 2y = x² . log x
∴ \(\frac{d y}{d x}+\left(\frac{2}{x}\right) \cdot y=x \cdot \log x\) …….(1)
This is the linear differential equation of the form


This is the general solution.

Question 4.
(x + y)\(\frac{d y}{d x}\) = 1
Solution:
(x + y) \(\frac{d y}{d x}\) = 1
∴ \(\frac{d x}{d y}\) = x + y
∴ \(\frac{d x}{d y}\) – x = y
∴ \(\frac{d x}{d y}\) + (-1) x = y ……(1)
This is the linear differential equation of the form

This is the general solution.

Question 5.
y dx + (x – y²) dy = 0
Solution:
y dx + (x – y²) dy = 0
∴ y dx = -(x – y²) dy
∴ \(\frac{d x}{d y}=-\frac{\left(x-y^{2}\right)}{y}=-\frac{x}{y}+y\)
∴ \(\frac{d x}{d y}+\left(\frac{1}{y}\right) \cdot x=y\) ……(1)
This is the linear differential equation of the form

This is the general solution.

Question 6.
\(\frac{d y}{d x}\) + 2xy = x
Solution:
\(\frac{d y}{d x}\) + 2xy = x ………(1)
This is the linear differential equation of the form

This is the general solution.

Question 7.
(x + a) \(\frac{d y}{d x}\) = -y + a
Solution:
(x + a) \(\frac{d y}{d x}\) + y = a
∴ \(\frac{d y}{d x}+\left(\frac{1}{x+a}\right) y=\frac{a}{x+a}\) ……..(1)
This is the linear differential equation of the form

This is the general solution.

Question 8.
dy + (2y) dx = 8 dx
Solution:
dy + (2y) dx = 8 dx
∴ \(\frac{d y}{d x}\) + 2y = 8 …….(1)
This is the linear differential equation of the form

This is the general solution.

Balbharati Maharashtra State Board 12th Commerce Maths Solution Book Pdf Chapter 8 Probability Distributions Miscellaneous Exercise 8 Questions and Answers.

Maharashtra State Board 12th Commerce Maths Solutions Chapter 8 Probability Distributions Miscellaneous Exercise 8

(I) Choose the correct alternative.

Question 1.
F(x) is c.d.f. of discreter r.v. X whose p.m.f. is given by P(x) = \(k\left(\begin{array}{l}
4 \\
x
\end{array}\right)\), for x = 0, 1, 2, 3, 4 & P(x) = 0 otherwise then F(5) = __________
(a) \(\frac{1}{16}\)
(b) \(\frac{1}{8}\)
(c) \(\frac{1}{4}\)
(d) 1
Answer:
(d) 1

Question 2.
F(x) is c.d.f. of discrete r.v. X whose distribution is

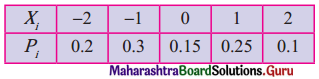
then F(-3) = __________
(a) 0
(b) 1
(c) 0.2
(d) 0.15
Answer:
(a) 0

Question 3.
X : number obtained on uppermost face when a fair die is thrown then E(X) = __________
(a) 3.0
(b) 3.5
(c) 4.0
(d) 4.5
Answer:
(b) 3.5

Question 4.
If p.m.f. of r.v. X is given below.

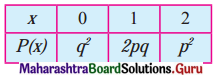
then Var(X) = __________
(a) p²
(b) q²
(c) pq
(d) 2pq
Answer:
(d) 2pq

Question 5.
The expected value of the sum of two numbers obtained when two fair dice are rolled is __________
(a) 5
(b) 6
(c) 7
(d) 8
Answer:
(c) 7

Question 6.
Given p.d.f. of a continuous r.v. X as
f(x) = \(\frac{x^{2}}{3}\) for -1 < x < 2
= 0 otherwise then F(1) =
(a) \(\frac{1}{9}\)
(b) \(\frac{2}{9}\)
(c) \(\frac{3}{9}\)
(d) \(\frac{4}{9}\)
Answer:
(b) \(\frac{2}{9}\)

Question 7.
X is r.v. with p.d.f.
f(x) = \(\frac{k}{\sqrt{x}}\), 0 < x < 4
= 0 otherwise then E(X) = __________
(a) \(\frac{1}{3}\)
(b) \(\frac{4}{3}\)
(c) \(\frac{2}{3}\)
(d) 1
Answer:
(b) \(\frac{4}{3}\)

Question 8.
If X follows B(20, \(\frac{1}{10}\)) then E(X) = __________
(a) 2
(b) 5
(c) 4
(d) 3
Answer:
(a) 2

Question 9.
If E(X) = m and Var(X) = m then X follows __________
(a) Binomial distribution
(b) Possion distribution
(c) Normal distribution
(d) none of the above
Answer:
(b) Possion distribution

Question 10.
If E(X) > Var(X) then X follows __________
(a) Binomial distribution
(b) Possion distribution
(c) Normal distribution
(d) none of the above
Answer:
(a) Binomial distribution

(II) Fill in the blanks.

Question 1.
The values of discrete r.v. are generally obtained by __________
Answer:
counting

Question 2.
The values of continuous r.v. are generally obtained by __________
Answer:
measurement

Question 3.
If X is dicrete random variable takes the values x₁, x₂, x₃, …… x_n then \(\sum_{i=1}^{n} p\left(x_{i}\right)\) = __________
Answer:
1

Question 4.
If f(x) is distribution function of discrete r.v. X with p.m.f. p(x) = \(\frac{x-1}{3}\) for x = 1, 2, 3, and p(x) = 0 otherwise then F(4) = __________
Answer:
1

Question 5.
If f(x) is distribution function of discrete r.v. X with p.m.f. p(x) = \(k\left(\begin{array}{l}
4 \\
x
\end{array}\right)\) for x = 0, 1, 2, 3, 4, and p(x) = 0 otherwise then F(-1) = __________
Answer:
0

Question 6.
E(X) is considered to be __________ of the probability distribution of X.
Answer:
centre of gravity

Question 7.
If X is continuous r.v. and f(x_i) = P(X ≤ x_i) = \(\int_{-\infty}^{x_{i}} f(x) d x\) then f(x) is called __________
Answer:
Cumulative Distribution Function

Question 8.
In Binomial distribution probability of success ________ from trial to trial.
Answer:
remains constant/independent

Question 9.
In Binomial distribution, if n is very large and probability success of p is very small such that np = m (constant) then ________ distribution is applied.
Answer:
Possion

(III) State whether each of the following is True or False.

Question 1.
If P(X = x) = \(k\left(\begin{array}{l}
4 \\
x
\end{array}\right)\) for x = 0, 1, 2, 3, 4, then F(5) = \(\frac{1}{4}\) when f(x) is c.d.f.
Answer:
False

Question 2.

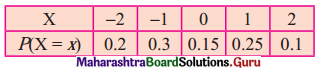
If F(x) is c.d.f. of discrete r.v. X then F(-3) = 0.
Answer:
True

Question 3.
X is the number obtained on the uppermost face when a die is thrown the E(X) = 3.5.
Answer:
True

Question 4.
If p.m.f. of discrete r.v.X is

then E(X) = 2p.
Answer:
True

Question 5.
The p.m.f. of a r.v. X is p(x) = \(\frac{2 x}{n(n+1)}\), x = 1, 2,……n
= 0 otherwise,
Then E(X) = \(\frac{2 n+1}{3}\)
Answer:
True

Question 6.
If f(x) = kx (1 – x) for 0 < x < 1
= 0 otherwise then k = 12
Answer:
False

Question 7.
If X ~ B(n, p) and n = 6 and P(X = 4) = P(X = 2) then p = \(\frac{1}{2}\).
Answer:
True

Question 8.
If r.v. X assumes values 1, 2, 3,………, n with equal probabilities then E(X) = \(\frac{(n+1)}{2}\)
Answer:
True

Question 9.
If r.v. X assumes the values 1, 2, 3,………, 9 with equal probabilities, E(X) = 5.
Answer:
True

(IV) Solve the following problems.

Part – I

Question 1.
Identify the random variable as discrete or continuous in each of the following. Identify its range if it is discrete.
(i) An economist is interested in knowing the number of unemployed graduates in the town with a population of 1 lakh.
Solution:
X = No. of unemployed graduates in a town.
∵ The population of the town is 1 lakh
∴ X takes finite values
∴ X is a Discrete Random Variable
∴ Range of = {0, 1, 2, 4, …. 1,00,000}

(ii) Amount of syrup prescribed by a physician.
Solution:
X : Amount of syrup prescribed.
∴ X Takes infinite values
∴ X is a Continuous Random Variable.

(iii) A person on a high protein diet is interested in the weight gained in a week.
Solution:
X : Gain in weight in a week.
X takes infinite values
∴ X is a Continuous Random Variable.

(iv) Twelve of 20 white rats available for an experiment are male. A scientist randomly selects 5 rats and counts the number of female rats among them.
Solution:
X : No. of female rats selected
X takes finite values.
∴ X is a Discrete Random Variable.
Range of X = {0, 1, 2, 3, 4, 5}

(v) A highway safety group is interested in the speed (km/hrs) of a car at a checkpoint.
Solution:
X : Speed of car in km/hr
X takes infinite values
∴ X is a Continuous Random Variable.

Question 2.
The probability distribution of a discrete r.v. X is as follows.

(i) Determine the value of k.
(ii) Find P(X ≤ 4), P(2 < X < 4), P(X ≥ 3).
Solution:
(i) Assuming that the given distribution is a p.m.f. of X
∴ Each P(X = x) ≥ 0 for x = 1, 2, 3, 4, 5, 6
k ≥ 0
ΣP(X = x) = 1 and
k + 2k + 3k + 4k + 5k + 6k = 1
∴ 21k = 1 ∴ k = \(\frac{1}{21}\)

(ii) P(X ≤ 4) = 1 – P(X > 4)
= 1 – [P(X = 5) + P(X = 6)]
= 1 – [latex]\frac{5}{21}+\frac{6}{21}[/latex]
= 1 – \(\frac{11}{21}\)
= \(\frac{10}{21}\)
P(2 < X < 6) = p(3) + p(4) + p(5)
= 3k + 4k + 5k
= \(\frac{3}{21}+\frac{4}{21}+\frac{5}{21}\)
= \(\frac{12}{21}\)
= \(\frac{4}{7}\)

(iii) P(X ≥ 3) = p(3) + p(4) + p(5) + p(6)
= 3k + 4k + 5k + 6k

Question 3.
Following is the probability distribution of an r.v. X.

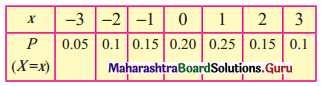
Find the probability that
(i) X is positive.
(ii) X is non-negative.
(iii) X is odd.
(iv) X is even.
Solution:
(i) P(X is positive)
P(X = 0) = p(1) + p(2) + p(3)
= 0.25 + 0.15 + 0.10
= 0.50

(ii) P(X is non-negative)
P(X ≥ 0) = p(0) + p(1) + p(2) + p(3)
= 0.20 + 0.25 + 0.15 + 0.10
= 0.70

(iii) P(X is odd)
P(X = -3, -1, 1, 3)
= p(- 3) +p(-1) + p(1) + p(3)
= 0.05 + 0.15 + 0.25 + 0.10
= 0.55

(iv) P(X is even)
= 1 – P(X is odd)
= 1 – 0.55
= 0.45

Question 4.
The p.m.f of a r.v. X is given by
\(P(X=x)= \begin{cases}\left(\begin{array}{l}
5 \\
x
\end{array}\right) \frac{1}{2^{5}}, & x=0,1,2,3,4,5 . \\
0 & \text { otherwise }\end{cases}\)
Show that P(X ≤ 2) = P(X ≥ 3).
Solution:
For x = 0, 1, 2, 3, 4, 5

Question 5.
In the following probability distribution of an r.v. X

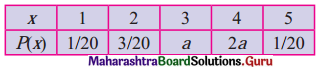
Find a and obtain the c.d.f. of X.
Solution:
Given distribution is p.m.f. of r.v. X
ΣP(X = x) = 1
∴ p(1) + p(2) + p(3) + p(4) + p(5) = 1

Question 6.
A fair coin is tossed 4 times. Let X denote the number of heads obtained. Identify the probability distribution of X and state the formula for p.m.f. of X.
Solution:
A fair coin is tossed 4 times
∴ Sample space contains 16 outcomes
Let X = Number of heads obtained
∴ X takes the values x = 0, 1, 2, 3, 4.
∴ The number of heads obtained in a toss is an even

Question 7.
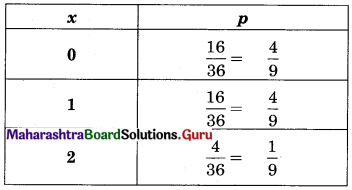
Find the probability of the number of successes in two tosses of a die, where success is defined as (i) number greater than 4 (ii) six appearing in at least one toss.
Solution:
S : A die is tossed two times
S = {(1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6), (2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6), (3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6), (4, 1), (4, 2), (4, 3), (4, 4), (4, 5), (4, 6), (5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6), (6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6)}
n(S) = 36
(i) X : No. is greater than 4
Range of X = {0, 1, 2}

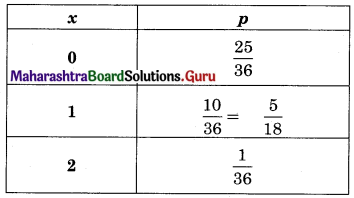
(ii) X : Six appears on aleast one die.
Range of X = {0, 1, 2}

Question 8.
A random variable X has the following probability distribution.

Determine (i) k, (ii) P(X < 3), (iii) P(X > 6), (iv) P(0 < X < 3).
Solution:
(i) It is a p.m.f. of r.v. X
Σp(x) = 1
p(1) + p(2) + p(3) + p(4) + p(5) + p(6) + p(7) = 1
k + 2k + 2k + 3k + k² + 2k² + 7k² + k = 1
9k + 10k² = 1
10k² + 9k – 1 = 0
10k² +10k – k – 1 = 0
∴ 10k(k + 1) – 1(k + 1) = 0
∴ (10k – 1) (k + 1) = 0
∴ 10k – 1 = 0r k + 1 = 0
∴ k = \(\frac{1}{10}\) or k = -1
k = -1 is not accepted, p(x) ≥ 0, ∀ x ∈ R
∴ k = \(\frac{1}{10}\)

(ii) P(X < 3) = p(1) + p(2)
= k + 2k
= 3k
= 3 × \(\frac{1}{10}\)
= \(\frac{3}{10}\)

(iii) P(X > 6) = p(7)
= 7k² + k
= \(7\left(\frac{1}{10}\right)^{2}+\frac{1}{10}\)
= \(\frac{7}{100}+\frac{1}{10}\)
= \(\frac{17}{100}\)

(iv) P(0 < X < 3) = p(1) + p(2)
= k + 2k
= 3k
= 3 × \(\frac{1}{10}\)
= \(\frac{3}{10}\)

Question 9.
The following is the c.d.f. of a r.v. X.

Find the probability distribution of X and P(-1 ≤ X ≤ 2).
Solution:

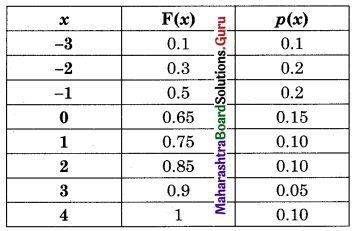
P(-1 ≤ X ≤ 2) = p(-1) + p(0) + p(1) + p(2)
= 0.2 + 0.15 + 0.10 + 0.10
= 0.55

Question 10.
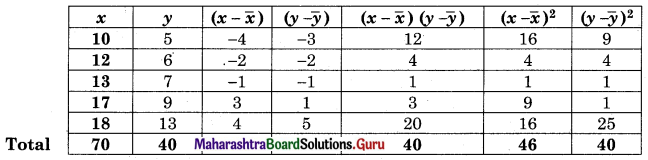
Find the expected value and variance of the r.v. X if its probability distribution is as follows.
(i)

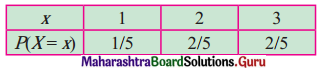
Solution:

(ii)

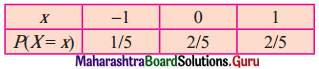
Solution:
E(X) = Σx . p(x)

(iii)

Solution:

(iv)

Solution:

= 1.25
S.D. of X = σ_x = √Var(X)
= √1.25
= 1.118

Question 11.
A player tosses two coins. He wins ₹ 10 if 2 heads appear, ₹ 5 if 1 head appears, and ₹ 2 if no head appears. Find the expected value and variance of the winning amount.
Solution:
S : Two fair coin are tossed
S = {HH, HT, TT, TH}
n(S) = 4
∴ Range of X = {0, 1, 2}
∴ Let Y = amount received corresponds to values of X

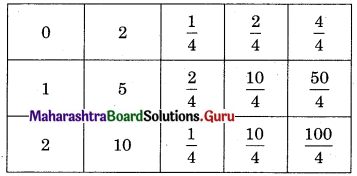
Expected winning amount
E(Y) = Σpy = \(\frac{22}{4}\) = ₹ 5.5
V(Y) = Σpy² – (Σpy)²
= \(\frac{154}{4}\) – (5.5)²
= 38.5 – 30.25
= ₹ 8.25

Question 12.
Let the p.m.f. of the r.v. X be
\(p(x)= \begin{cases}\frac{3-x}{10} & \text { for } x=-1,0,1,2 \\ 0 & \text { otherwise }\end{cases}\)
Calculate E(X) and Var(X).
Solution:

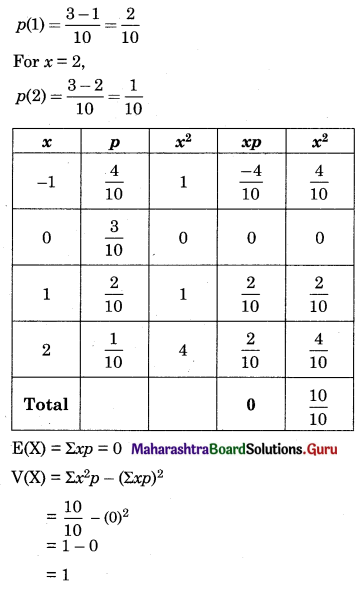
Question 13.
Suppose error involved in making a certain measurement is a continuous r.v. X with p.d.f.
\(f(x)= \begin{cases}k\left(4-x^{2}\right) & \text { for }-2 \leq x \leq 2 \\ 0 & \text { otherwise }\end{cases}\)
Compute (i) P(X > 0), (ii) P(-1 < X < 1), (iii) P(X < -0.5 or X > 0.5)
Solution:
We know that

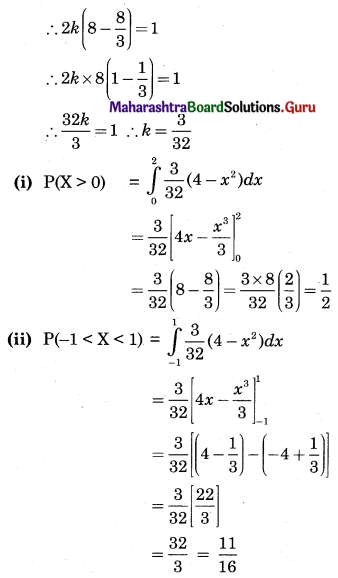
Question 14.
The p.d.f. of the r.v. X is given by
\(f(x)= \begin{cases}\frac{1}{2 a} & \text { for } 0<x<2 a \\ 0 & \text { otherwise }\end{cases}\)
Show that P(X < \(\frac{a}{2}\)) = P(X > \(\frac{3a}{2}\))
Solution:

Question 15.
Determine k if
\(f(x)= \begin{cases}k e^{-\theta x} & \text { for } 0 \leq x<\infty, \theta>0 \\ 0 & \text { otherwise }\end{cases}\)
is the p.d.f. of the r.v. X. Also find P(X > \(\frac{1}{\theta}\)). Find M if P(0 < X < M) = \(\frac{1}{2}\)
Solution:
We know that

Question 16.
The p.d.f. of the r.v. X is given by
\(f_{x}(x)=\left\{\begin{array}{l}
\frac{k}{\sqrt{x}}, 0<x<4 \\
0, \text { otherwise }
\end{array}\right.\)
Determine k, c.d.f. of X and hence find P(X ≤ 2) and P(X ≥ 1).
Solution:
We know that

Question 17.
Let X denote the reaction temperature (in °C) of a certain chemical process. Let X be a continuous r.v. with p.d.f.
\(f(x)= \begin{cases}\frac{1}{10}, & -5 \leq x \leq 5 \\ 0, & \text { otherwise }\end{cases}\)
Compute P(X < 0).
Solution:
Given p.d.f. is f(x) = \(\frac{1}{10}\), for -5 ≤ x ≤ 5
Let its c.d.f. F(x) be given by

Part – II

Question 1.
Let X ~ B(10, 0.2). Find (i) P(X = 1) (ii) P(X ≥ 1) (iii) P(X ≤ 8)
Solution:
X ~ B(10, 0.2)
n = 10, p = 0.2
∴ q = 1 – p = 1 – 0.2 = 0.8
(i) P(X = 1) = ¹⁰C₁ (0.2)¹ (0.8)⁹ = 0.2684

(ii) P(X ≥ 1) = 1 – P(X < 1)
= 1 – P(X = 0)
= 1 – ¹⁰C₀ (0.2)⁰ (0.8)¹⁰
= 1 – 0.1074
= 0.8926

(iii) P(X ≤ 8) = 1 – P(x > 1)
= 1 – [p(9) + p(10)]
= 1 – [¹⁰C₉ (0.2)⁹ (0.8)¹ + ¹⁰C₁₀ (0.2)¹⁰]
= 1 – 0.00000041984
= 0.9999

Question 2.
Let X ~ B(n, p) (i) If n = 10 and E(X) = 5, find p and Var(X), (ii) If E(X) = 5 and Var(X) = 2.5, find n and p.
Solution:
X ~ B(n, p)
(i) n = 10, E(X) = 5
∴ np = 5
∴ 10p = 5
∴ p = \(\frac{1}{2}\)
∴ q = 1 – p = 1 – \(\frac{1}{2}\) = \(\frac{1}{2}\)
V(X) = npq
= 10 × \(\frac{1}{2}\) × \(\frac{1}{2}\)
= 2.5

(ii) E(X) = 5, V(X) = 2.5
∴ np = 5, ∴ npq = 2.5
∴ 5q = 2.5
∴ q = \(\frac{2.5}{5}\) = 0.5, p = 1 – 0.5 = 0.5
But np = 5
∴ n(0.5) = 5
∴ n = 10

Question 3.
If a fair coin is tossed 4 times, find the probability that it shows (i) 3 heads, (ii) head in the first 2 tosses, and tail in the last 2 tosses.
Solution:
n : No. of times a coin is tossed
∴ n = 4
X : No. of heads
P : Probability of getting heads

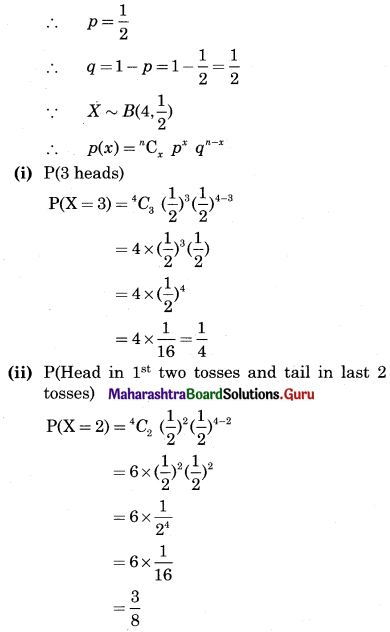
Question 4.
The probability that a bomb will hit the target is 0.8. Find the probability that, out of 5 bombs, exactly 2 will miss the target.
Solution:
X : No. of bombs miss the target
p : Probability that bomb miss the target
∴ q = 0.8
∴ p = 1 – q = 1 – 0.8 = 0.2
n = No. of bombs = 5
∴ X ~ B(5, 0.2)
∴ p(x) = ⁿC_x p^x q^n-x
P(X = 2) = ⁵C₂ (0.2)² (0.8)^5-2
= 10 × 0.04 × (0.8)³
= 10 × 0.04 × 0.512
= 0.4 × 0.512
= 0.2048

Question 5.
The probability that a lamp in the classroom will burn is 0.3. 3 lamps are fitted in the classroom. The classroom is unusable if the number of lamps burning in it is less than 2. Find the probability that the classroom can not be used on a random occasion.
Solution:
X : No. of lamps not burning
p : Probability that the lamp is not burning
∴ q = 0.3
∴ p = 1 – q = 1 – 0.3 = 0.7
n = No. of lamps fitted = 3
∴ X ~ B(3, 0.7)
∴ p(x) = ⁿC_x p^x q^n-x
P(classroom cannot be used)
P(X < 2) = p(0) + p(1)
= ³C₀ (0.7)⁰ (0.3)^3-0 + ³C₁ (0.7)¹ (0.3)^3-1
= 1 × 1 × (0.3)³ + 3 × 0.7 × (0.3)²
= (0.3)2 [0.3 + 3 × 0.7]
= 0.09 [0.3 + 2.1]
= 0.09 [2.4]
= 0.216

Question 6.
A large chain retailer purchases an electric device from the manufacturer. The manufacturer indicates that the defective rate of the device is 10%. The inspector of the retailer randomly selects 4 items from a shipment. Find the probability that the inspector finds at most one defective item in the 4 selected items.
Solution:
X : No. of defective items
n : No. of items selected = 4
p : Probability of getting defective items
∴ p = 0.1
∴ q = 1 – p = 1 – 0.1 = 0.9
P(At most one defective item)
P(X ≤ 1) = p(0) + p(1)
= ⁴C₀ (0.1)⁰ (0.9)^4-0 + ⁴C₁ (0.1)¹ (0.9)^4-1
= 1 × 1 × (0.9)⁴ + 4 × 0.1 × (0.9)³
= (0.9)3 [0.9 + 4 × 0.1]
= (0.9)3 × [0.9 + 0.4]
= 0.729 × 1.3
= 0.9477

Question 7.
The probability that a component will survive a check test is 0.6. Find the probability that exactly 2 of the next 4 components tested survive.
Solution:
p = 0.6, q = 1 – 0.6 = 0.4, n = 4
x = 2
∴ p(x) = ⁿC_x p^x q^n-x
P(X = 2) = ⁴C₂ (0.6)² (0.4)² = 0.3456

Question 8.
An examination consists of 5 multiple choice questions, in each of which the candidate has to decide which one of 4 suggested answers is correct. A completely unprepared student guesses each answer randomly. Find the probability that this student gets 4 or more correct answers.
Solution:
n : No. of multiple-choice questions
∴ n = 5
X : No. of correct answers
p : Probability of getting correct answer
∵ There are 4 options out of which one is correct
∴ p = \(\frac{1}{4}\)
∴ q = 1 – p = 1 – \(\frac{1}{4}\) = \(\frac{3}{4}\)
∵ X ~ B(5, \(\frac{1}{4}\))
∴ p(x) = ⁿC_x p^x q^n-x
P(Four or more correct answers)
P(X ≥ 4) = p(4) + p(5)

Question 9.
The probability that a machine will produce all bolts in a production run with in the specification is 0.9. A sample of 3 machines is taken at random. Calculate the probability that all machines will produce all bolts in a production run within the specification.
Solution:
n : No. of samples selected
∴ n = 3
X : No. of bolts produce by machines
p : Probability of getting bolts
∴ p = 0.9
∴ q = 1 – p = 1 – 0.9 = 0.1
∴ X ~ B(3, 0.9)
∴ p(x) = ⁿC_x p^x q^n-x
P(Machine will produce all bolts)
P(X = 3) = ³C₃ (0.9)³ (0.1)^3-3
= 1 × (0.9)³ × (0.1)⁰
= 1 × (0.9)³ × 1
= (0.9)³
= 0.729

Question 10.
A computer installation has 3 terminals. The probability that anyone terminal requires attention during a week is 0.1, independent of other terminals. Find the probabilities that (i) 0 (ii) 1 terminal requires attention during a week.
Solution:
n : No. of terminals
∴ n = 3
X : No. of terminals need attention
p : Probability of getting terminals need attention
∴ p = 0.1
∴ q = 1 – p = 1 – 0.1 = 0.9
∵ X ~ B(3, 0.1)
∴ p(x) = ⁿC_x p^x q^n-x
(i) P(No attention)
∴ P(X = 0) = ³C₀ × (0.1)⁰ (0.9)^3-1
= 1 × 1 × (0.9)³
= 0.729

(ii) P(One terminal need attention)
∴ P(X = 1) = ³C₁ (0.1)¹ (0.9)^3-1
= 3 × 0.1 × (0.9)²
= 0.3 × 0.81
= 0.243

Question 11.
In a large school, 80% of the students like mathematics. A visitor asks each of 4 students, selected at random, whether they like mathematics, (i) Calculate the probabilities of obtaining an answer yes from all of the selected students, (ii) Find the probability that the visitor obtains the answer yes from at least 3 students.
Solution:
X : No. of students like mathematics
p: Probability that students like mathematics
∴ p = 0.8
∴ q = 1 – p = 1 – 0.8 = 0.2
n : No. of students selected
∴ n = 4
∵ X ~ B(4, 0.8)
∴ p(x) = ⁿC_x p^x q^n-x
(i) P(All students like mathematics)
∴ P(X = 4) = ⁴C₄ (0.8)⁴ (0.2)^4-4
= 1 × (0.8)⁴ × (0.2)⁰
= 1 × (0.8)⁴ × 1
= 0.4096

(ii) P(Atleast 3 students like mathematics)
∴ P(X ≥ 3) = p(3) + p(4)
= ⁴C₃ (0.8)³ (0.2)^4-3 + 0.4096
= 4 × (0.8)³ (0.2)¹ + 0.4096
= 0.8 × (0.8)³ + 0.4096
= (0.8)⁴ × 0.4096
= 0.4096 + 0.4096
= 0.8192

Question 12.
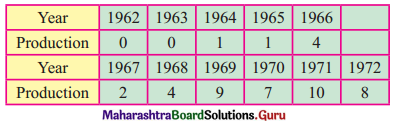
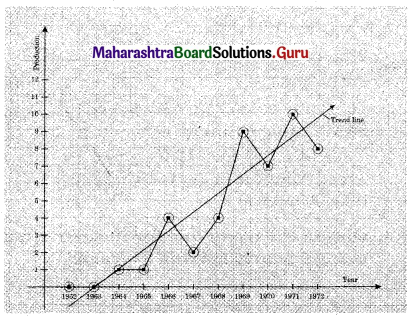
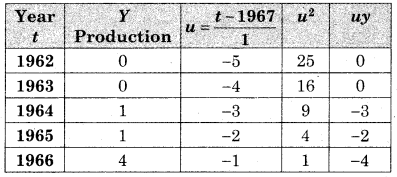
It is observed that it rains on 10 days out of 30 days. Find the probability that
(i) it rains on exactly 3 days of a week.
(ii) it rains at most 2 days a week.
Solution:
X : No. of days it rains in a week
p : Probability that it rains
∴ p = \(\frac{10}{30}=\frac{1}{3}\)
∴ q = 1 – p = 1 – \(\frac{1}{3}\) = \(\frac{2}{3}\)
n : No. of days in a week
∴ n = 7
∴ X ~ B(7, \(\frac{1}{3}\))
(i) P(Rains on Exactly 3 days of a week)

(ii) P(Rains on at most 2 days of a week)
∴ P(X ≤ 2) = p(0) + p(1) + p(2)

Question 13.
If X follows Poisson distribution such that P(X = 1) = 0.4 and P(X = 2) = 0.2, find variance of X.
Solution:
X : Follows Possion Distribution

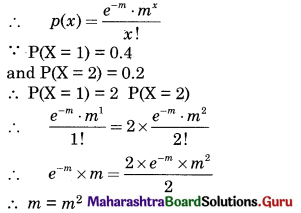
∴ m = 1
∴ Mean = m = Variance of X = 1

Question 14.
If X has Poisson distribution with parameter m, such that
\(\frac{P(X=x+1)}{P(X=x)}=\frac{m}{x+1}\)
find probabilities P(X = 1) and P(X = 2), when X follows Poisson distribution with m = 2 and P(X = 0) = 0.1353.
Solution:
Given that the random variable X follows the Poisson distribution with parameter m = 2
i.e. X ~ P(2)
Its p.m.f. is satisfying the given equation.
\(\frac{P(X=x+1)}{P(X=x)}=\frac{m}{x+1}\)
When x = 0,
\(\frac{\mathrm{P}(\mathrm{X}=1)}{\mathrm{P}(\mathrm{X}=0)}=\frac{2}{0+1}\)
P(X = 1) = 2P(X = 0)
= 2(0.1353)
= 0.2706
When x = 1,
\(\frac{\mathrm{P}(\mathrm{X}=2)}{\mathrm{P}(\mathrm{X}=1)}=\frac{2}{1+1}\)
P(X = 2) = P(X = 1) = 0.2706

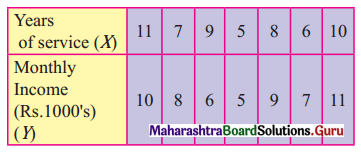
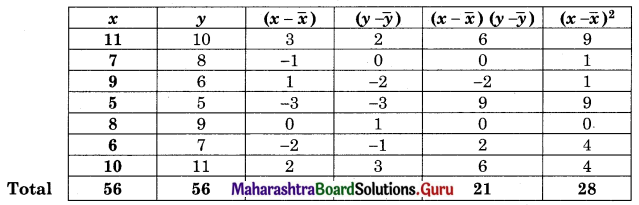
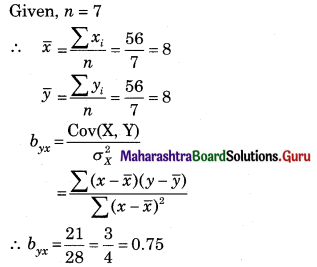
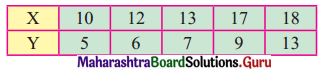
Balbharati Maharashtra State Board Std 12 Commerce Statistics Part 1 Digest Pdf Chapter 8 Differential Equation and Applications Ex 8.4 Questions and Answers.

Maharashtra State Board 12th Commerce Maths Solutions Chapter 8 Differential Equation and Applications Ex 8.4

Solve the following differential equations:

Question 1.
x dx + 2y dy = 0
Solution:
x dx + 2y dy = 0
Integrating, we get
∫x dx + 2 ∫y dy = c₁
∴ \(\frac{x^{2}}{2}+2\left(\frac{y^{2}}{2}\right)=c_{1}\)
∴ x² + 2y² = c, where c = 2c₁
This is the general solution.

Question 2.
y² dx + (xy + x²) dy = 0
Solution:
y² dx + (xy + x²) dy = 0
∴ (xy + x²) dy = -y² dx
∴ \(\frac{d y}{d x}=\frac{-y^{2}}{x y+x^{2}}\) ………(1)
Put y = vx
∴ \(\frac{d y}{d x}=v+x \frac{d v}{d x}\)
Substituting these values in (1), we get



This is the general solution.

Question 3.
x²y dx – (x³ + y³) dy = 0
Solution:
x²y dx – (x³ + y³) dy = 0
∴ (x³ + y³) dy = x²y dx
∴ \(\frac{d y}{d x}=\frac{x^{2} y}{x^{3}+y^{3}}\) ……(1)
Put y = vx
∴ \(\frac{d y}{d x}=v+x \frac{d v}{d x}\)


This is the general solution.

Question 4.
\(\frac{d y}{d x}+\frac{x-2 y}{2 x-y}=0\)
Solution:



This is the general solution.

Question 5.
(x² – y²) dx + 2xy dy = 0
Solution:
(x² – y²) dx + 2xy dy = 0
∴ 2xy dy = -(x² – y²) dx = (y² – x²) dx
∴ \(\frac{d y}{d x}=\frac{y^{2}-x^{2}}{2 x y}\) ………(1)

Question 6.
xy\(\frac{d y}{d x}\) = x² + 2y²
Solution:

Question 7.
x²\(\frac{d y}{d x}\) = x² + xy – y²
Solution:

Balbharati Maharashtra State Board 12th Commerce Maths Digest Pdf Chapter 4 Time Series Ex 4.1 Questions and Answers.

Maharashtra State Board 12th Commerce Maths Solutions Chapter 4 Time Series Ex 4.1

Question 1.
The following data gives the production of bleaching powder (in ‘000 tonnes) for the years 1962 to 1972.

Fit a trend line by graphical method to the above data.
Solution:

Question 2.
Use the method of least squares to fit a trend line to the data in problem 1 above. Also, obtain the trend value for the year 1975.
Solution:


n = 11, let the trend line the
y = a + bu ……..(I)
Σy = na + bΣu ……..(i)
Σuy = aΣu + bΣu² ………(ii)
Substituting the values of Σy, Σu, Σuy, & Σu², we get
46 = 11a + 0
∴ a = 4.18 And
114 = 0 + b(110)
∴ b = 1.04
By (I) the equation of the trends line is
y = 4.18 + 1.04u
Where u = t – 1967 ……..(iii)
For the year 1975 we have u = 8
Substituting in (iii) we get
Y= 4.18 + 1.04(8) = 12.5
Trend value for the year 1975 is 12.5 (in ‘000 tonnes).

Question 3.
Obtain the trend line for the above data using 5 yearly moving averages.
Solution:

Question 4.
The following table shows the index of industrial production for the period from 1976 to 1985, using the year 1976 as the base year.

Fit a trend line to the above data by graphical method.
Solution:

Question 5.
Fit a trend line to the data in problem 4 above by the method of least squares. Also, obtain the trend value for the index of industrial production for the year 1987.
Solution:


u = \(\frac{t-1980.5}{\frac{1}{2}}\), n = 10, Σu = 0, Σy = 42, Σu² = 330, Σuy = 148
Let the trend line be y = a + bu ……(i)
where u = \(\frac{t-1980.5}{\frac{1}{2}}\)
i.e. u = 2t – 3961
Σy = na + bΣu ……(ii)
Σuy = aΣu + bΣu² ……….(iii)
Substituting the values of Σy, n, Σu, Σuy & Σu² We get
42 = 10a + 0
∴ a = 4.2 and
148 = 0 + 5.330
∴ b = 0.4485
∴ by (i) the equation of the trends line is
Y = 4.2 + 0.4485u ………(iv)
where u = 2t – 3961
For the year 1987,
u = 13 by (iv) we have
Y = 4.2 + 0.4485(13) = 10.0305
∴ The trend value for the year 1987 is 10.0305

Question 6.
Obtain the trend values for the data in problem 4 using 4-yearly centered moving averages.
Solution:

Question 7.
The following table gives the production of steel (in millions of tonnes) for the years 1976 to 1986.

Fit a trend line to the above data by the graphical method.
Solution:

Question 8.
Fit a trend line to the data in Problem 7 by the method of least squares. Also, obtain the trend value for the year 1990.
Solution:

u = \(\frac{t-1981}{1}\), n = 10, Σu = 0, ΣY = 62, Σu² = 110, Σuy = 87
Let the equation of the trend line be
Y = a + bu
where u = t – 1981 ……(i)
ΣY = na + bΣu ………(ii)
Σuy = aΣu + bΣu² ………(iii)
Substituting the values of Σy, n, Σu, Σuy, Σu² in (ii) & (iii)
62 = 11a + 0
∴ a = 5.6364 And
87 = 0 + 5(110)
∴ b = 0.7909
∴ by (i) equation of the trend line is y = 5.6364 + 0.7909u
Where u = t – 1981
For the year 1990,
u = 9
∴ y = 5.6364 + 0.7909(9)
∴ y = 12.7545 (in million tonnes)

Question 9.
Obtain the trend values for the above data using 3-yearly moving averages.
Solution:

Question 10.
The following table shows the production of gasoline in the U.S.A. for the years 1962 to 1976.

(i) Obtain trend values for the above data using 5-yearly moving averages.
(ii) Plot the original time series and trend values obtained above on the same graph.
Solution:
(i)

(ii)

Balbharati Maharashtra State Board Std 12 Commerce Statistics Part 1 Digest Pdf Chapter 8 Differential Equation and Applications Ex 8.3 Questions and Answers.

Maharashtra State Board 12th Commerce Maths Solutions Chapter 8 Differential Equation and Applications Ex 8.3

Question 1.
Solve the following differential equations:
(i) \(\frac{d y}{d x}\) = x²y + y
Solution:
\(\frac{d y}{d x}\) = x²y + y
∴ \(\frac{d y}{d x}\) = y(x² + 1)
∴ \(\frac{1}{y}\) dy = (x² + 1) dx
Integrating, we get
∫\(\frac{1}{y}\) dy = ∫(x² + 1) dx
∴ log |y|= \(\frac{x^{3}}{3}\) + x + c
This is the general solution.

(ii) \(\frac{d \theta}{d t}=-k\left(\theta-\theta_{0}\right)\)
Solution:
\(\frac{d \theta}{d t}=-k\left(\theta-\theta_{0}\right)\)

This is the general solution.

(iii) (x² – yx²) dy + (y² + xy²) dx = 0
Solution:
(x² – yx²) dy + (y² + xy²) dx = 0
∴ x²(1 – y) dy + y²(1 + x) dx = 0
∴ \(\frac{1-y}{y^{2}} d y+\frac{1+x}{x^{2}} d x=0\)
Integrating, we get


This is the general solution.

(iv) \(y^{3}-\frac{d y}{d x}=x \frac{d y}{d x}\)
Solution:
\(y^{3}-\frac{d y}{d x}=x \frac{d y}{d x}\)

∴ 2y² log |x + 1| = 2cy² – 1 is the required solution.

Question 2.
For each of the following differential equations find the particular solution:
(i) (x – y²x) dx – (y + x²y) dy = 0, when x = 2, y = 0.
Solution:
(x – y²x) dx – (y + x²y) dy = 0
∴ x(1 – y²) dx – y(1 + x²) dy = 0

∴ the general solution is
log |1 + x²| + log |1 – y²| = log c, where c₁ = log c
∴ log |(1 + x²)(1 – y²) | = log c
∴ (1 + x²)(1 – y²) = c
When x = 2, y = 0, we have
(1 + 4)(1 – 0) = c
∴ c = 5
∴ the particular solution is (1 + x²)(1 – y²) = 5.

(ii) (x + 1) \(\frac{d y}{d x}\) -1 = 2e^-y, when y = 0, x = 1.
Solution:

∴ log |2 + e^y| = log |c(x + 1)|
∴ 2 + e^y = c(x + 1)
This is the general solution.
Now, y = 0, when x = 1
∴ 2 + e⁰ = c(1 + 1)
∴ 3 = 2c
∴ c = \(\frac{3}{2}\)
∴ the particular solution is
2 + e^y = \(\frac{3}{2}\)(x + 1)
∴ 4 + 2e^y = 3x + 3
∴ 3x – 2e^y – 1 = 0

(iii) y(1 + log x) \(\frac{d x}{d y}\) – x log x = 0, when x = e, y = e².
Solution:

∴ from (1), the general solution is
log |x log x| – log |y| = log c, where c₁ = log c
∴ log |\(\frac{x \log x}{y}\)| = log c
∴ \(\frac{x \log x}{y}\) = c
∴ x log x = cy
This is the general solution.
Now, y = e², when x = e
e log e = ce²
1 = ce ……[∵ log e = 1]
c = \(\frac{1}{e}\)
∴ the particular solution is x log x = (\(\frac{1}{e}\)) y
∴ y = e^x log x

(iv) \(\frac{d y}{d x}\) = 4x + y + 1, when y = 1, x = 0.
Solution:
\(\frac{d y}{d x}\) = 4x + y + 1
Put 4x + y + 1 = v

∴ log |v + 4| = x + c
∴ log |4x + y + 1 + 4| = x + c
i.e. log |4x + y + 5| = x + c
This is the general solution.
Now, y = 1 when x = 0
∴ log|0 + 1 + 5| = 0 + c,
i.e. c = log 6
∴ the particular solution is
log |4x + y + 5| = x + log 6
∴ \(\log \left|\frac{4 x+y+5}{6}\right|\) = x

Balbharati Maharashtra State Board 12th Commerce Maths Solution Book Pdf Chapter 5 Index Numbers Ex 5.3 Questions and Answers.

Maharashtra State Board 12th Commerce Maths Solutions Chapter 5 Index Numbers Ex 5.3

Calculate the cost of living index in problems 1 to 3.

Question 1.

Solution:

Question 2.

Solution:

Question 3.

Solution:

Base year weights (W) and current year price relatives (I) are given in problems 4 to 8. Calculate the cost of living index in each case.

Question 4.

Solution:

ΣW = 20, ΣIW = 1540
CLI = \(\frac{\sum \mathrm{IW}}{\sum \mathrm{W}}\)
= \(\frac{1540}{20}\)
= 77

Question 5.

Solution:

ΣW = 17, ΣIW = 3500
CLI = \(\frac{\sum \mathrm{IW}}{\sum \mathrm{W}}\)
= \(\frac{3500}{17}\)
= 205.88

Question 6.

Solution:

ΣW = 150, ΣIW = 25400
CLI = \(\frac{\sum \mathrm{IW}}{\sum \mathrm{W}}\)
= \(\frac{25400}{150}\)
= 169.33

Question 7.

Solution:

ΣW = x + 18, ΣIW = 100x + 3600
CLI = 150
∴ \(\frac{\sum \mathrm{IW}}{\sum \mathrm{W}}\) = 150
∴ \(\frac{100 x+3600}{x+18}\) = 150
∴ 100x + 3600 = 150x + 2700
∴ 50x = 900
∴ x = 18

Question 8.
Find y if the cost of living index is 200

Solution:

ΣW = y + 18, ΣIW = 300y + 2200
CLI = 200
∴ \(\frac{\sum \mathrm{IW}}{\sum \mathrm{W}}\) = 200
∴ \(\frac{300 y+2200}{y+14}\) = 200
∴ 300y + 2200 = 200y + 2800
∴ 100y = 600
∴ y = 6

Question 9.
The cost of living Index numbers for years 1995 and 1999 are 140 and 200 respectively. A person earns ₹ 11,200 per month in the year 1995. What should be his monthly earning in the year 1999 in order to maintain his standard of living as in the year 1995?
Solution:
CLI (1995) = 140
CLI (1999) = 200
Income (1995) = 11200
Income (1999) = ?
For year 1995
∴ Real Income = \(\frac{\text { Income }}{\text { CLI }} \times 100\)
= \(\frac{11200}{140}\) × 100
= ₹ 8000
For year 1999
∴ Real Income = \(\frac{\text { Income }}{\text { CLI }} \times 100\)
∴ 8000 = \(\frac{\text { Income } \times 100}{200}\)
∴ Income = 16000
∴ Income in 1999 = ₹ 16000

Balbharati Maharashtra State Board 12th Commerce Maths Solution Book Pdf Chapter 5 Index Numbers Ex 5.2 Questions and Answers.

Maharashtra State Board 12th Commerce Maths Solutions Chapter 5 Index Numbers Ex 5.2

Calculate Laspeyres, Paasche’s, Dorbish-Bowely’s, and Marshall-Edegworth’s Price Index Numbers in Problems 1 and 2.

Question 1.

Solution:

Question 2.

Solution:

Calculate Walsh’s Price Index Number in Problems 3 and 4.

Question 3.

Solution:

Question 4.

Solution:

Question 5.
If p₀₁(L) = 90, and p₀₁(P) = 40, find p₀₁(D – B) and p₀₁(F)
Solution:

Question 6.
If Σp₀q₀ = 140, Σp₀q₁ = 200, Σp₁q₀ = 350, Σp₁q₁ = 460, find Laspeyre’s Paasche’s Dorbish-Bowley’s and Marshall- Edgeworth’s Price Index Numbers.
Solution:

Question 7.
Given that Laspeyre’s and Dorbish-Bowley’s Price Index Numbers are 160.32 and 164.18 respectively. Find Paasche’s Price Index Number.
Solution:

Question 8.
Given that Σp₀q₀ = 220, Σp₀q₁ = 380, Σp₁q₁ = 350 is Marshall-Edgeworth’s Price Index Number is 150, find Laspeyre’s Price Index Number.
Solution:

Question 9.
Find x in the following table if Laspeyres and Paasche’s Price Index Numbers are equal.

Solution:

Question 10.
If Laspeyre’s Price Index Number is four times Paasche’s Price Index Number, then find the relation between Dorbish-Bowley’s and Fisher’s Price Index Numbers.
Solution:

Question 11.
If Dorbish-Bowley’s and Fisher’s Price Index Numbers are 5 and 4, respectively, then find Laspeyres and Paasche’s Price Index Numbers.
Solution: