Class 11

Balbharti Maharashtra State Board 11th Maths Book Solutions Pdf Chapter 4 Methods of Induction and Binomial Theorem Ex 4.3 Questions and Answers.

Maharashtra State Board 11th Maths Solutions Chapter 4 Methods of Induction and Binomial Theorem Ex 4.3

Question 1.
In the following expansions, find the indicated term.
(i) \(\left(2 x^{2}+\frac{3}{2 x}\right)^{8}\), 3rd term
Solution:

(ii) \(\left(x^{2}-\frac{4}{x^{3}}\right)^{11}\), 5th term
Solution:

(iii) \(\left(\frac{4 x}{5}-\frac{5}{2 x}\right)^{9}\), 7th term
Solution:

(iv) In \(\left(\frac{1}{3}+a^{2}\right)^{12}\), 9th term
Solution:

(v) In \(\left(3 a+\frac{4}{a}\right)^{13}\), 10th term
Solution:

Question 2.
In the following expansions, find the indicated coefficients.
(i) x³ in \(\left(x^{2}+\frac{3 \sqrt{2}}{x}\right)^{9}\)
Solution:

(ii) x⁸ in \(\left(2 x^{5}-\frac{5}{x^{3}}\right)^{8}\)
Solution:

(iii) x⁹ in \(\left(\frac{1}{x}+x^{2}\right)^{18}\)
Solution:

(iv) x^-3 in \(\left(x-\frac{1}{2 x}\right)^{5}\)
Solution:

(v) x^-20 in \(\left(x^{3}-\frac{1}{2 x^{2}}\right)^{15}\)
Solution:

Question 3.
Find the constant term (term independent of x) in the expansion of
(i) \(\left(2 x+\frac{1}{3 x^{2}}\right)^{9}\)
Solution:

(ii) \(\left(x-\frac{2}{x^{2}}\right)^{15}\)
Solution:

(iii) \(\left(\sqrt{x}-\frac{3}{x^{2}}\right)^{10}\)
Solution:

(iv) \(\left(x^{2}-\frac{1}{x}\right)^{9}\)
Solution:

(v) \(\left(2 x^{2}-\frac{5}{x}\right)^{9}\)
Solution:

Question 4.
Find the middle terms in the expansion of
(i) \(\left(\frac{x}{y}+\frac{y}{x}\right)^{12}\)
Solution:

(ii) \(\left(x^{2}+\frac{1}{x}\right)^{7}\)
Solution:

(iii) \(\left(x^{2}-\frac{2}{x}\right)^{8}\)
Solution:

(iv) \(\left(\frac{x}{a}-\frac{a}{x}\right)^{10}\)
Solution:

(v) \(\left(x^{4}-\frac{1}{x^{3}}\right)^{11}\)
Solution:

Question 5.
In the expansion of (k + x)⁸, the coefficient of x⁵ is 10 times the coefficient of x⁶. Find the value of k.
Solution:

Question 6.
Find the term containing x⁶ in the expansion of (2 – x) (3x + 1)⁹.
Solution:

Question 7.
The coefficient of x² in the expansion of (1 + 2x)^m is 112. Find m.
Solution:
The coefficient of x² in (1 + 2x)^m = ^mC₂ (2²)
Given that the coefficient of x² = 112
∴ ^mC₂ (4) = 112
∴ ^mC₂ = 28
∴ \(\frac{\mathrm{m} !}{2 !(\mathrm{m}-2) !}=28\)
∴ \(\frac{m(m-1)(m-2) !}{2 \times(m-2) !}=28\)
∴ m(m – 1) = 56
∴ m² – m – 56 = 0
∴ (m – 8) (m + 7) = 0
As m cannot be negative.
∴ m = 8

Balbharti Maharashtra State Board Class 11 Maths Solutions Pdf Chapter 4 Methods of Induction and Binomial Theorem Ex 4.2 Questions and Answers.

Maharashtra State Board 11th Maths Solutions Chapter 4 Methods of Induction and Binomial Theorem Ex 4.2

Question 1.
Expand:
(i) (√3 + √2)⁴
Solution:
Here, a = √3, b = √2 and n = 4.
Using binomial theorem,

∴ (√3 + √2)⁴ = 1(9) (1) + 4(3√3) (√2) + 6(3)(2) + 4(√3) (2√2) + 1(1)(4)
= 9 + 12√6 + 36 + 8√6 + 4
= 49 + 20√6

(ii) (√5 – √2)⁵
Solution:
Here, a = √5, b = √2 and n = 5.
Using binomial theorem,

Question 2.
Expand:
(i) (2x² + 3)⁴
Solution:
Here, a = 2x², b = 3 and n = 4.
Using binomial theorem,

(ii) \(\left(2 x-\frac{1}{x}\right)^{6}\)
Solution:
Here, a = 2x, b = \(\frac{1}{x}\) and n = 6.
Using binomial theorem,

Question 3.
Find the value of
(i) (√3 + 1)⁴ – (√3 – 1)⁴
Solution:

(ii) (2 + √5)⁵ + (2 – √5)⁵
Solution:


Adding (i) and (ii), we get
∴ (2 + √5 )⁵ + (2 – √5)⁵ = (32 + 80√5 + 400 + 200√5 + 250 + 25√5) + (32 – 80√5 + 400 – 200√5+ 250 – 25√5 )
= 64 + 800 + 500
= 1364

Question 4.
Prove that:
(i) (√3 + √2)⁶ + (√3 – √2)⁶ = 970
Solution:

(ii) (√5 + 1)⁵ – (√5 – 1)⁵ = 352
Solution:

Question 5.
Using binomial theorem, find the value of
(i) (102)⁴
Solution:

(ii) (1.1)⁵
Solution:

Question 6.
Using binomial theorem, find the value of
(i) (9.9)³
Solution:

(ii) (0.9)⁴
Solution:

Question 7.
Without expanding, find the value of
(i) (x + 1)⁴ – 4(x + 1)³ (x – 1) + 6(x + 1)² (x – 1)² – 4(x + 1) (x – 1)³ + (x – 1)⁴
Solution:

(ii) (2x – 1)⁴ + 4(2x – 1)³ (3 – 2x) + 6(2x – 1)² (3 – 2x)² + 4(2x – 1)¹ (3 – 2x)³ + (3 – 2x)⁴
Solution:

Question 8.
Find the value of (1.02)⁶, correct upto four places of decimals.
Solution:

Question 9.
Find the value of (1.01)⁵, correct upto three places of decimals.
Solution:

Question 10.
Find the value of (0.9)⁶, correct upto four places of decimals.
Solution:

Balbharti Maharashtra State Board 11th Maths Book Solutions Pdf Chapter 2 Sequences and Series Ex 2.5 Questions and Answers.

Maharashtra State Board 11th Maths Solutions Chapter 2 Sequences and Series Ex 2.5

Question 1.
Find Sn of the following arithmetico-geometric sequences.
(i) 2, 4x, 6x², 8x³, 10x⁴, ……
Solution:
2, 4x, 6x², 8x³, 10x⁴, ……
Here, 2, 4, 6, 8, 10,… are in A.P.
∴ a = 2, d = 2
∴ nth term = a + (n – 1)d
= 2 + (n – 1)(2)
= 2n

(ii) 1, 4x, 7x², 10x³, 13x⁴, ……
Solution:
1, 4x, 7x², 10x³, 13x⁴, ……
Here, 1, 4, 7, 10, 13,… are in A.P.
a = 1, d = 3
∴ nth term = a + (n – 1)d
= 1 + (n – 1)(3)
= 3n – 2
Also, 1, x, x², x³,… are in G.P.
∴ a = 1, r = x,
nth term = ar^n-1 = x^n-1
nth term of arithmetico-geometric sequence is

(iii) 1, 2 × 3, 3 × 9, 4 × 27, 5 × 81, ……
Solution:
1, 2 × 3, 3 × 9, 4 × 27, 5 × 81, …..
Here, 1, 2, 3, 4, 5, … are in A.P.
∴ a = 1, d = 1
∴ nth term = a + (n – 1)d
= 1 + (n – 1)1
= n

(iv) 3, 12, 36, 96, 240, ……
Solution:
3, 12, 36, 96, 240, ……
i.e., 1 × 3, 2 × 6, 3 × 12, 4 × 24, 5 × 48, …….
Here, 1, 2, 3, 4, 5, ….. are in A.P.
∴ nth term = n
Also, 3, 6, 12, 24, 48, ….. are in G.P.
∴ a = 3, r = 2
∴ nth term = ar^n-1 = 3 . (2^n-1)
∴ nth term of arithmetico-geometric sequence is

Question 2.
Find the sum to infinity of the following arithmetico-geometric sequence.
(i) \(1, \frac{2}{4}, \frac{3}{16}, \frac{4}{64}, \ldots\)
Solution:

(ii) \(3, \frac{6}{5}, \frac{9}{25}, \frac{12}{125}, \frac{15}{625}, \ldots\)
Solution:

∴ \(\frac{4}{5} S=\frac{15}{4}\)
∴ S = \(\frac{75}{16}\)

(iii) \(1, \frac{-4}{3}, \frac{7}{9}, \frac{-10}{27} \ldots\)
Solution:

Balbharti Maharashtra State Board 11th Maths Book Solutions Pdf Chapter 9 Differentiation Miscellaneous Exercise 9 Questions and Answers.

Maharashtra State Board 11th Maths Solutions Chapter 9 Differentiation Miscellaneous Exercise 9

(I) Select the appropriate option from the given alternatives.

Question 1.
If y = \(\frac{x-4}{\sqrt{x+2}}\), then \(\frac{d y}{d x}\) is
(A) \(\frac{1}{x+4}\)
(B) \(\frac{\sqrt{x}}{\left(\sqrt{x+2)^{2}}\right.}\)
(C) \(\frac{1}{2 \sqrt{x}}\)
(D) \(\frac{x}{(\sqrt{x}+2)^{2}}\)
Answer:
(C) \(\frac{1}{2 \sqrt{x}}\)
Hint:

Question 2.
If y = \(\frac{a x+b}{c x+d}\),then \(\frac{d y}{d x}\) =
(A) \(\frac{a b-c d}{(c x+d)^{2}}\)
(B) \(\frac{a x-c}{(c x+d)^{2}}\)
(C) \(\frac{a c-b d}{(c x+d)^{2}}\)
(D) \(\frac{a d-b c}{(c x+d)^{2}}\)
Answer:
(D) \(\frac{a d-b c}{(c x+d)^{2}}\)
Hint:

Question 3.
If y = \(\frac{3 x+5}{4 x+5}\), then \(\frac{d y}{d x}\) =
(A) \(-\frac{15}{(3 x+5)^{2}}\)
(B) \(-\frac{15}{(4 x+5)^{2}}\)
(C) \(-\frac{5}{(4 x+5)^{2}}\)
(D) \(-\frac{13}{(4 x+5)^{2}}\)
Answer:
(C) \(-\frac{5}{(4 x+5)^{2}}\)
Hint:

Question 4.
If y = \(\frac{5 \sin x-2}{4 \sin x+3}\), then \(\frac{d y}{d x}\) =
(A) \(\frac{7 \cos x}{(4 \sin x+3)^{2}}\)
(B) \(\frac{23 \cos x}{(4 \sin x+3)^{2}}\)
(C) \(-\frac{7 \cos x}{(4 \sin x+3)^{2}}\)
(D) \(-\frac{15 \cos x}{(4 \sin x+3)^{2}}\)
Answer:
(B) \(\frac{23 \cos x}{(4 \sin x+3)^{2}}\)
Hint:

Question 5.
Suppose f(x) is the derivative of g(x) and g(x) is the derivative of h(x).
If h(x) = a sin x + b cos x + c, then f(x) + h(x) =
(A) 0
(B) c
(C) -c
(D) -2(a sin x + b cos x)
Answer:
(B) c
Hint:
h(x) = a sin x + b cos x + c
Differentiating w.r.t. x, we get
h'(x) = a cos x – b sin x = g(x) …..[given]
Differentiating w.r.t. x, we get
g'(x) = -a sin x – b cos x = f(x) …..[given]
∴ f(x) + h(x) = -a sin x – b cos x + a sin x + b cos x + c
∴ f(x) + h(x) = c

Question 6.
If f(x) = 2x + 6, for 0 ≤ x ≤ 2
= ax² + bx, for 2 < x ≤ 4
is differentiable at x = 2, then the values of a and b are
(A) a = \(-\frac{3}{2}\), b = 3
(B) a = \(\frac{3}{2}\), b = 8
(C) a = \(\frac{1}{2}\), b = 8
(D) a = \(-\frac{3}{2}\), b = 8
Answer:
(D) a = \(-\frac{3}{2}\), b = 8
Hint:
f(x) = 2x + 6, 0 ≤ x ≤ 2
= ax² + bx, 2 < x ≤ 4
Lf'(2) = 2, Rf'(2) = 4a + b
Since f is differentiable at x = 2,
Lf'(2) = Rf'(2)
∴ 2 = 4a + b …..(i)
f is continuous at x = 2.
∴ \(\lim _{x \rightarrow 2^{+}} f(x)=f(2)=\lim _{x \rightarrow 2^{-}} f(x)\)
∴ 4a + 2b = 2(2) + 6
∴ 4a + 2b = 10
∴ 2a + b = 5 …..(ii)
Solving (i) and (ii), we get
a = \(-\frac{3}{2}\), b = 8

Question 7.
If f(x) = x² + sin x + 1, for x ≤ 0
= x² – 2x + 1, for x ≤ 0, then
(A) f is continuous at x = 0, but not differentiable at x = 0
(B) f is neither continuous nor differentiable at x = 0
(C) f is not continuous at x = 0, but differentiable at x = 0
(D) f is both continuous and differentiable at x = 0
Answer:
(A) f is continuous at x = 0, but not differentiable at x = 0
Hint:

Question 8.
If f(x) = \(\frac{x^{50}}{50}+\frac{x^{49}}{49}+\frac{x^{48}}{48}+\ldots .+\frac{x^{2}}{2}+x+1\), then f'(1) =
(A) 48
(B) 49
(C) 50
(D) 51
Answer:
(C) 50
Hint:

(II).

Question 1.
Determine whether the following function is differentiable at x = 3 where,
f(x) = x² + 2, for x ≥ 3
= 6x – 7, for x < 3.
Solution:
f(x) = x² + 2, x ≥ 3
= 6x – 7, x < 3
Differentiability at x = 3


Here, Lf'(3) = Rf'(3)
∴ f is differentiable at x = 3.

Question 2.
Find the values of p and q that make function f(x) differentiable everywhere on R.
f(x) = 3 – x, for x < 1
= px² + qx, for x ≥ 1.
Solution:
f(x) is differentiable everywhere on R.
∴ f(x) is differentiable at x = 1.
∴ f(x) is continuous at x = 1.

f(x) is differentiable at x = 1.
∴ Lf'(1) = Rf'(1)
∴ -1 = 2p + q …..(ii)
Subtracting (i) from (ii), we get
p = -3
Substituting p = -3 in (i), we get
p + q = 2
∴ -3 + q = 2
∴ q = 5

Question 3.
Determine the values of p and q that make the function f(x) differentiable on R where
f(x) = px³, for x < 2
= x² + q, for x ≥ 2
Solution:
f(x) is differentiable on R.
∴ f(x) is differentiable at x = 2.
∴ f(x) is continuous at x = 2.
Continuity at x = 2:
f(x) is continuous at x = 2.


f(x) is differentiable at x = 2.
∴ Lf'(2) = Rf'(2)
∴ 12p = 4
∴ p = \(\frac{1}{3}\)
Substituting p = \(\frac{1}{3}\) in (i), we get
8(\(\frac{1}{3}\) – q = 4
∴ q = \(\frac{8}{3}\) – 4 = \(\frac{-4}{3}\)

Question 4.
Determine all real values of p and q that ensure the function
f(x) = px + q, for x ≤ 1
= tan(\(\frac{\pi x}{4}\)), for 1 < x < 2
is differentiable at x = 1.
Solution:
f(x) is differentiable at x = 1.
∴ f(x) is continuous at x = 1.
Continuity at x= 1:
f(x) is continuous at x = 1.

Question 5.
Discuss whether the function f(x) = |x + 1| + |x – 1| is differentiable ∀ x ∈ R.
Solution:


Here, Lf'(1) ≠ Rf'(1)
∴ f is not differentiable at x = 1.
∴ f is not differentiable at x = -1 and x = 1.
∴ f is not differentiable ∀ x ∈ R.

Question 6.
Test whether the function
f(x) = 2x – 3, for x ≥ 2
= x – 1, for x < 2
is differentiable at x = 2.
Solution:

Question 7.
Test whether the function
f(x) = x² + 1, for x ≥ 2
= 2x + 1, for x < 2
is differentiable at x = 2.
Solution:

Question 8.
Test whether the function
f(x) = 5x – 3x², for x ≥ 1
= 3 – x, for x < 1
is differentiable at x = 1.
Solution:

Here, Lf'(1) = Rf'(1)
∴ f(x) is differentiable at x = 1.

Question 9.
If f(2) = 4, f'(2) = 1, then find \(\lim _{x \rightarrow 2}\left[\frac{x f(2)-2 f(x)}{x-2}\right]\)
Solution:

Question 10.
If y = \(\frac{\mathbf{e}^{x}}{\sqrt{x}}\), find \(\frac{d y}{d x}\) when x = 1.
Solution:

Balbharti Maharashtra State Board 11th Maths Book Solutions Pdf Chapter 6 Functions Ex 6.1 Questions and Answers.

Maharashtra State Board 11th Maths Solutions Chapter 6 Functions Ex 6.1

Question 1.
Check if the following relations are functions.
(a)

Solution:
Yes.
Reason: Every element of set A has been assigned a unique element in set B.

(b)

Solution:
No.
Reason: An element of set A has been assigned more than one element from set B.

(c)

Solution:
No.
Reason:
Not every element of set A has been assigned an image from set B.

Question 2.
Which sets of ordered pairs represent functions from A = {1, 2, 3, 4} to B = {-1, 0, 1, 2, 3}? Justify.
(i) {(1, 0), (3, 3), (2, -1), (4, 1), (2, 2)}
(ii) {(1, 2), (2, -1), (3, 1), (4, 3)}
(iii) {(1, 3), (4, 1), (2, 2)}
(iv) {(1, 1), (2, 1), (3, 1), (4, 1)}
Solution:
(i) {(1, 0), (3, 3), (2, -1), (4, 1), (2, 2)} does not represent a function.
Reason: (2, -1), (2, 2), show that element 2 ∈ A has been assigned two images -1 and 2 from set B.

(ii) {(1, 2), (2, -1), (3, 1), (4, 3)} represents a function.
Reason: Every element of set A has been assigned a unique image in set B.

(iii) {(1, 3), (4, 1), (2, 2)} does not represent a function.
Reason:
3 ∈ A does not have an image in set B.

(iv) {(1, 1), (2, 1), (3, 1), (4, 1)} represents a function
Reason: Every element of set A has been assigned a unique image in set B.

Question 3.
Check if the relation given by the equation represents y as function of x.
(i) 2x + 3y = 12
(ii) x + y² = 9
(iii) x² – y = 25
(iv) 2y + 10 = 0
(v) 3x – 6 = 21
Solution:
(i) 2x + 3y = 12
∴ y = \(\frac{12-2 x}{3}\)
∴ For every value of x, there is a unique value of y.
∴ y is a function of x.

(ii) x + y² = 9
∴ y² = 9 – x
∴ y = ±\(\sqrt{9-x}\)
∴ For one value of x, there are two values of y.
∴ y is not a function of x.

(iii) x² – y = 25
∴ y = x² – 25
∴ For every value of x, there is a unique value of y.
∴ y is a function of x.

(iv) 2y + 10 = 0
∴ y = -5
∴ For every value of x, there is a unique value of y.
∴ y is a function of x.

(v) 3x – 6 = 21
∴ x = 9
∴ x = 9 represents a point on the X-axis.
There is no y involved in the equation.
So the given equation does not represent a function.

Question 4.
If f(m) = m² – 3m + 1, find
(i) f(0)
(ii) f(-3)
(iii) f(\(\frac{1}{2}\))
(iv) f(x + 1)
(v) f(-x)
(vi) \(\left(\frac{\mathbf{f}(2+h)-f(2)}{h}\right)\), h ≠ 0.
Solution:
f(m) = m² – 3m + 1
(i) f(0) = 0² – 3(0) + 1 = 1

(ii) f (-3) = (-3)² – 3(-3) + 1
= 9 + 9 + 1
= 19

(iii) f(\(\frac{1}{2}\)) = \(\left(\frac{1}{2}\right)^{2}-3\left(\frac{1}{2}\right)+1\)
= \(\frac{1}{4}-\frac{3}{2}+1\)
= \(\frac{1-6+4}{4}\)
= \(-\frac{1}{4}\)

(iv) f(x + 1) = (x + 1)² – 3(x + 1) + 1
= x² + 2x + 1 – 3x – 3 + 1
= x² – x – 1

(v) f(-x) = (-x)2 – 3(-x) + 1 = x2 + 3x + 1

(vi) \(\left(\frac{\mathbf{f}(2+h)-f(2)}{h}\right)\)
= \(\frac{(2+h)^{2}-3(2+h)+1-\left(2^{2}-3(2)+1\right)}{h}\)
= \(\frac{\mathrm{h}^{2}+\mathrm{h}}{\mathrm{h}}\)
= h + 1

Question 5.
Find x, if g(x) = 0 where
(i) g(x) = \(\frac{5 x-6}{7}\)
(ii) g(x) = \(\frac{18-2 x^{2}}{7}\)
(iii) g(x) = 6x² + x – 2
(iv) g(x) = x³ – 2x² – 5x + 6
Solution:
(i) g(x) = \(\frac{5 x-6}{7}\)
g(x) = 0
∴ \(\frac{5 x-6}{7}\) = 0
∴ x = \(\frac{6}{5}\)

(ii) g(x) = \(\frac{18-2 x^{2}}{7}\)
g(x) = 0
\(\frac{18-2 x^{2}}{7}\) = 0
∴ 18 – 2x² = 0
∴ x² = 9
∴ x = ±3

(iii) g(x) = 6x² + x – 2
g(x) = 0
∴ 6x² + x – 2 = 0
∴ (2x – 1) (3x + 2) = 0
∴ 2x – 1 = 0 or 3x + 2 = 0
∴ x = \(\frac{1}{2}\) or x = \(\frac{-2}{3}\)

(iv) g(x) = x³ – 2x² – 5x + 6
= ( x- 1) (x² – x – 6)
= (x – 1) (x + 2) (x – 3)
g(x) = 0
∴ (x – 1) (x + 2) (x – 3) = 0
∴ x – 1 = 0 or x + 2 = 0 or x – 3 = 0
∴ x = 1, -2, 3

Question 6.
Find x, if f(x) = g(x) where
(i) f(x) = x⁴ + 2x², g(x) = 11x²
(ii) f(x) = √x – 3, g(x) = 5 – x
Solution:
(i) f(x) = x⁴ + 2x², g(x) = 11x²
f(x) = g(x)
∴ x⁴ + 2x² = 11x²
∴ x⁴ – 9x² = 0
∴ x² (x² – 9) = 0
∴ x² = 0 or x² – 9 = 0
∴ x = 0 or x² = 9
∴ x = 0, ±3

(ii) f(x) = √x – 3, g(x) = 5 – x
f(x) = g(x)
∴ √x – 3 = 5 – x
∴ √x = 5 – x + 3
∴ √x = 8 – x
on squaring, we get
x = 64 + x² – 16x
∴ x² – 17x + 64 = 0
∴ x = \(\frac{17 \pm \sqrt{(-17)^{2}-4(64)}}{2}\)
∴ x = \(\frac{17 \pm \sqrt{289-256}}{2}\)
∴ x = \(\frac{17 \pm \sqrt{33}}{2}\)

Question 7.
If f(x) = \(\frac{a-x}{b-x}\), f(2) is undefined, and f(3) = 5, find a and b.
Solution:
f(x) = \(\frac{a-x}{b-x}\)
Given that,
f(2) is undefined
b – 2 = 0
∴ b = 2 …..(i)
f(3) = 5
∴ \(\frac{a-3}{b-3}\) = 5
∴ \(\frac{a-3}{2-3}\) = 5 ….. [From (i)]
∴ a – 3 = -5
∴ a = -2
∴ a = -2, b = 2

Question 8.
Find the domain and range of the following functions.
(i) f(x) = 7x² + 4x – 1
Solution:
f(x) = 7x² + 4x – 1
f is defined for all x.
∴ Domain of f = R (i.e., the set of real numbers)

∴ Range of f = [\(-\frac{11}{7}\), ∞)

(ii) g(x) = \(\frac{x+4}{x-2}\)
Solution:
g(x) = \(\frac{x+4}{x-2}\)
Function g is defined everywhere except at x = 2.
∴ Domain of g = R – {2}
Let y = g(x) = \(\frac{x+4}{x-2}\)
∴ (x – 2) y = x + 4
∴ x(y – 1) = 4 + 2y
∴ For every y, we can find x, except for y = 1.
∴ y = 1 ∉ range of function g
∴ Range of g = R – {1}

(iii) h(x) = \(\frac{\sqrt{x+5}}{5+x}\)
Solution:
h(x) = \(\frac{\sqrt{x+5}}{5+x}=\frac{1}{\sqrt{x+5}}\), x ≠ -5
For x = -5, function h is not defined.
∴ x + 5 > 0 for function h to be well defined.
∴ x > -5
∴ Domain of h = (-5, ∞)
Let y = \(\frac{1}{\sqrt{x+5}}\)
∴ y > 0
Range of h = (0, ∞) or R+

(iv) f(x) = \(\sqrt[3]{x+1}\)
Solution:
f(x) = \(\sqrt[3]{x+1}\)
f is defined for all real x and the values of f(x) ∈ R
∴ Domain of f = R, Range of f = R

(v) f(x) = \(\sqrt{(x-2)(5-x)}\)
Solution:
f(x) = \(\sqrt{(x-2)(5-x)}\)
For f to be defined,
(x – 2)(5 – x) ≥ 0
∴ (x – 2)(x – 5) ≤ 0
∴ 2 ≤ x ≤ 5 ……[∵ The solution of (x – a) (x – b) ≤ 0 is a ≤ x ≤ b, for a < b]
∴ Domain of f = [2, 5]
(x – 2) (5 – x) = -x² + 7x – 10
= \(-\left(x-\frac{7}{2}\right)^{2}+\frac{49}{4}-10\)
= \(\frac{9}{4}-\left(x-\frac{7}{2}\right)^{2} \leq \frac{9}{4}\)
∴ \(\sqrt{(x-2)(5-x)} \leq \sqrt{\frac{9}{4}} \leq \frac{3}{2}\)
Range of f = [0, \(\frac{3}{2}\)]

(vi) f(x) = \(\sqrt{\frac{x-3}{7-x}}\)
Solution:
f(x) = \(\sqrt{\frac{x-3}{7-x}}\)
For f to be defined,
\(\sqrt{\frac{x-3}{7-x}}\) ≥ 0, 7 – x ≠ 0
∴ \(\sqrt{\frac{x-3}{7-x}}\) ≤ 0 and x ≠ 7
∴ 3 ≤ x < 7
Let a < b, \(\frac{x-a}{x-b}\) ≤ 0 ⇒ a ≤ x < b
∴ Domain of f = [3, 7)
f(x) ≥ 0 … [∵ The value of square root function is non-negative]
∴ Range of f = [0, ∞)

(vii) f(x) = \(\sqrt{16-x^{2}}\)
Solution:
f(x) = \(\sqrt{16-x^{2}}\)
For f to be defined,
16 – x² ≥ 0
∴ x² ≤ 16
∴ -4 ≤ x ≤ 4
∴ Domain of f = [-4, 4]
Clearly, f(x) ≥ 0 and the value of f(x) would be maximum when the quantity subtracted from 16 is minimum i.e. x = 0
∴ Maximum value of f(x) = √16 = 4
∴ Range of f = [0, 4]

Question 9.
Express the area A of a square as a function of its
(a) side s
(b) perimeter P
Solution:
(a) area (A) = s²
(b) perimeter (P) = 4s
∴ s = \(\frac{\mathrm{P}}{4}\)
Area (A) = s² = \(\left(\frac{\mathrm{P}}{4}\right)^{2}\)
∴ A = \(\frac{\mathrm{P}^{2}}{16}\)

Question 10.
Express the area A of a circle as a function of its
(i) radius r
(ii) diameter d
(iii) circumference C
Solution:
(i) Area (A) = πr²

(ii) Diameter (d) = 2r
∴ r = \(\frac{\mathrm{d}}{2}\)
∴ Area (A) = πr² = \(\frac{\pi \mathrm{d}^{2}}{4}\)

(iii) Circumference (C) = 2πr
∴ r = \(\frac{C}{2 \pi}\)
Area (A) = πr² = \(\pi\left(\frac{\mathrm{C}}{2 \pi}\right)^{2}\)
∴ A = \(\frac{C^{2}}{4 \pi}\)

Question 11.
An open box is made from a square of cardboard of 30 cms side, by cutting squares of length x centimeters from each corner and folding the sides up. Express the volume of the box as a function of x. Also, find its domain.
Solution:

Length of the box = 30 – 2x
Breadth of the box = 30 – 2x
Height of the box = x
Volume = (30 – 2x)² x, x < 15, x ≠ 15, x > 0
= 4x(15 – x)², x ≠ 15, x > 0
Domain (0, 15)

Question 12.
Let f be a subset of Z × Z defined by f = {(ab, a + b): a, b ∈ Z}. Is f a function from Z to Z? Justify?
Solution:
f = {(ab, a + b): a, b ∈ Z}
Let a = 1, b = 1. Then, ab = 1, a + b = 2
∴ (1, 2) ∈ f
Let a = -1, b = -1. Then, ab = 1, a + b = -2
∴ (1, -2) ∈ f
Since (1, 2) ∈ f and (1, -2) ∈ f,
f is not a function as element 1 does not have a unique image.

Question 13.
Check the injectivity and surjectivity of the following functions.
(i) f : N → N given by f(x) = x²
Solution:
f: N → N given by f(x) = x²

∴ f is injective.
For every y = x² ∈ N, there does not exist x ∈ N.
Example: 7 ∈ N (codomain) for which there is no x in domain N such that x² = 7
∴ f is not surjective.

(ii) f : Z → Z given by f(x) = x²
Solution:
f: Z → Z given by f(x) = x2

∴ f is not injective.
(Example: f(-2) = 4 = f(2). So, -2, 2 have the same image. So, f is not injective.)
Since x² ≥ 0,
f(x) ≥ 0
Therefore all negative integers of codomain are not images under f.
∴ f is not surjective.

(iii) f : R → R given by f(x) = x²
Solution:
f : R → R given by f(x) = x²

∴ f is not injective.
f(x) = x² ≥ 0
Therefore all negative integers of codomain are not images under f.
∴ f is not surjective.

(iv) f : N → N given by f(x) = x³
Solution:
f: N → N given by f(x) = x³

∴ f is injective.
Numbers from codomain which are not cubes of natural numbers are not images under f.
∴ f is not surjective.

(v) f : R → R given by f(x) = x³
Solution:
f: R → R given by f(x) = x³

∴ For every y ∈ R, there is some x ∈ R.
∴ f is surjective.

Question 14.
Show that if f : A → B and g : B → C are one-one, then gof is also one-one.
Solution:
f is a one-one function.
Let f(x₁) = f(x₂)
Then, x₁ = x₂ for all x₁, x₂ …..(i)
g is a one-one function.
Let g(y₁) = g(y₂)
Then, y₁ = y₂ for all y₁, y₂ …..(ii)
Let (gof) (x₁) = (gof) (x₂)
∴ g(f(x₁)) = g(f(x₂))
∴ g(y₁) = g(y₂),
where y₁ = f(x₁), y₂ = f(x₂) ∈ B
∴ y₁ = y₂ …..[From (ii)]
i.e., f(x₁) = f(x₂)
∴ x₁ = x₂ ….[From (i)]
∴ gof is one-one.

Question 15.
Show that if f : A → B and g : B → C are onto, then gof is also onto.
Solution:
Since g is surjective (onto),
there exists y ∈ B for every z ∈ C such that
g(y) = z …….(i)
Since f is surjective,
there exists x ∈ A for every y ∈ B such that
f(x) = y …….(ii)
(gof) x = g(f(x))
= g(y) ……[From (ii)]
= z …..[From(i)]
i.e., for every z ∈ C, there is x in A such that (gof) x = z
∴ gof is surjective (onto).

Question 16.
If f(x) = 3(4^x+1), find f(-3).
Solution:
f(x) = 3(4^x+1)
∴ f(-3) = 3(4^-3+1)
= 3(4^-2)
= \(\frac{3}{16}\)

Question 17.
Express the following exponential equations in logarithmic form:
(i) 2⁵ = 32
(ii) 54⁰ = 1
(iii) 23¹ = 23
(iv) \(9^{\frac{3}{2}}\) = 27
(v) 3^-4 = \(\frac{1}{81}\)
(vi) 10^-2 = 0.01
(vii) e² = 7.3890
(viii) \(e^{\frac{1}{2}}\) = 1.6487
(ix) e^-x = 6
Solution:

Question 18.
Express the following logarithmic equations in exponential form:
(i) log₂ 64 = 6
(ii) \(\log _{5} \frac{1}{25}\) = -2
(iii) log₁₀ 0.001 = -3
(iv) \(\log _{\frac{1}{2}}\)(8) = -3
(v) ln 1 = 0
(vi) ln e = 1
(vii) ln \(\frac{1}{2}\) = -0.693
Solution:
(i) log₂ 64 = 6
∴ 64 = 2⁶, i.e., 2⁶ = 64

Question 19.
Find the domain of
(i) f(x) = ln (x – 5)
(ii) f(x) = log10 (x² – 5x + 6)
Solution:
(i) f(x) = ln (x – 5)
f is defined, when x – 5 > 0
∴ x > 5
∴ Domain of f = (5, ∞)

(ii) f(x) = log₁₀ (x² – 5x + 6)
x² – 5x + 6 = (x – 2) (x – 3)
f is defined, when (x – 2) (x – 3) > 0
∴ x < 2 or x > 3
Solution of (x – a) (x – b) > 0 is x < a or x > b where a < b
∴ Domain of f = (-∞, 2) ∪ (3, ∞)

Question 20.
Write the following expressions as sum or difference of logarithms:
(a) \(\log \left(\frac{p q}{r s}\right)\)
Solution:

(b) \(\log (\sqrt{x} \sqrt[3]{y})\)
Solution:

(c) \(\ln \left(\frac{a^{3}(a-2)^{2}}{\sqrt{b^{2}+5}}\right)\)
Solution:

(d) \(\ln \left[\frac{\sqrt[3]{x-2}(2 x+1)^{4}}{(x+4) \sqrt{2 x+4}}\right]^{2}\)
Solution:

Question 21.
Write the following expressions as a single logarithm.
(i) 5 log x + 7 log y – log z
Solution:

(ii) \(\frac{1}{3}\) log(x – 1) + \(\frac{1}{2}\) log(x)
Solution:

(iii) ln (x + 2) + ln (x – 2) – 3 ln (x + 5)
Solution:

Question 22.
Given that log 2 = a and log 3 = b, write log √96 terms of a and b.
Solution:
log 2 = a and log 3 = b
log √96 = \(\frac{1}{2}\) log (96)
= \(\frac{1}{2}\) log (2⁵ x 3)
= \(\frac{1}{2}\) (log 2⁵ + log 3) …..[∵ log mn = log m + log n]
= \(\frac{1}{2}\) (5 log 2 + log 3) ……[∵ log mⁿ = n log m]
= \(\frac{5 a+b}{2}\)

Question 23.
Prove that:
(a) \(b^{\log _{b} a}=a\)
Solution:
We have to prove that \(b^{\log _{b} a}=a\)
i.e., to prove that (logb a) (log_b b) = log_b a
(Taking log on both sides with base b)
L.H.S. = (log_b a) (log_b b)
= log_b a …..[∵ log_b b = 1]
= R.H.S.

(b) \(\log _{b^{m}} a=\frac{1}{m} \log _{b} a\)
Solution:

(c) \(a^{\log _{c} b}=b^{\log _{c} a}\)
Solution:

Question 24.
If f(x) = ax² – bx + 6 and f(2) = 3 and f(4) = 30, find a and b.
Solulion:
f(x) = ax² – bx + 6
f(2) = 3
∴ a(2)² – b(2) + 6 = 3
∴ 4a – 2b + 6 = 3
∴ 4a – 2b + 3 = 0 …..(i)
f(4) = 30
∴ a(4)² – b(4) + 6 = 30
∴ 16a – 4b + 6 = 30
∴ 16a – 4b – 24 = 0 …..(ii)
By (ii) – 2 × (i), we get
8a – 30 = 0
∴ a = \(\frac{30}{8}=\frac{15}{4}\)
Substiting a = \(\frac{15}{4}\) in (i), we get
4(\(\frac{15}{4}\)) – 2b + 3 = 0
∴ 2b = 18
∴ b = 9
∴ a = \(\frac{15}{4}\), b = 9

Question 25.
Solve for x:
(i) log 2 + log (x + 3) – log (3x – 5) = log 3
Solution:
log 2 + log (x + 3) – log (3x – 5) = log 3
∴ log 2(x + 3) – log(3x – 5) = log 3 …..[∵ log m + log n = log mn]
∴ log \(\frac{2(x+3)}{3 x-5}\) = log 3 …..[∵ log m – log n = log \(\frac{m}{n}\)]
∴ \(\frac{2(x+3)}{3 x-5}\) = 3
∴ 2x + 6 = 9x – 15
∴ 7x = 21
∴ x = 3

Check:
If x = 3 satisfies the given condition, then our answer is correct.
L.H.S. = log 2 + log (x + 3) – log (3x – 5)
= log 2 + log (3 + 3) – log (9 – 5)
= log 2 + log 6 – log 4
= log (2 × 6) – log 4
= log \(\frac{12}{4}\)
= log 3
= R.H.S.
Thus, our answer is correct.

(ii) 2log₁₀ x = 1 + \(\log _{10}\left(x+\frac{11}{10}\right)\)
Solution:


∴ x² = 10x + 11
∴ x² – 10x – 11 = 0
∴ (x – 11)(x + 1) = 0
∴ x = 11 or x = -1
But log of a negative numbers does not exist
∴ x ≠ -1
∴ x = 11

(iii) log₂ x + log₄ x + log₁₆ x = \(\frac{21}{4}\)
Solution:

(iv) x + log₁₀ (1 + 2^x) = x log₁₀ 5 + log₁₀ 6
Solution:

∴ a + a² = 6
∴ a² + a – 6 = 0
∴ (a + 3)(a – 2) = 0
∴ a + 3 = 0 or a – 2 = 0
∴ a = -3 or a = 2
Since 2x = -3 is not possible,
2x = 2 = 21
∴ x = 1

Question 26.
If log \(\left(\frac{x+y}{3}\right)\) = \(\frac{1}{2}\) log x + \(\frac{1}{2}\) log y, show that \(\frac{x}{y}+\frac{y}{x}\) = 7.
Solution:

Question 27.
If log\(\left(\frac{x-y}{4}\right)\) = log√x + log√y, show that (x + y)² = 20xy.
Solution:

Question 28.
If x = log_abc, y = log_b ca, z = log_c ab, then prove that \(\frac{1}{1+x}+\frac{1}{1+y}+\frac{1}{1+z}\) = 1.
Solution:

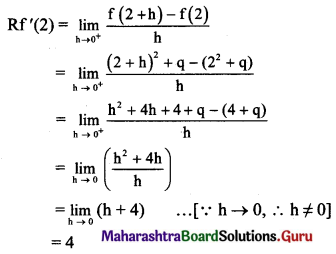
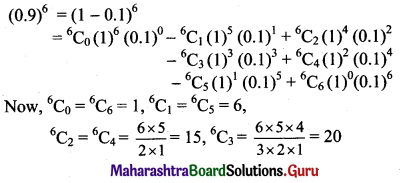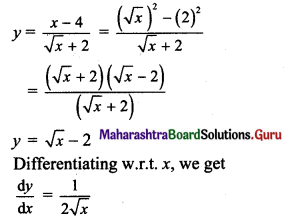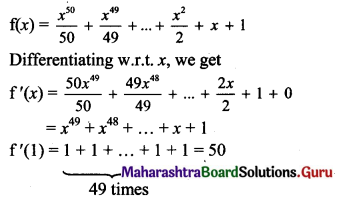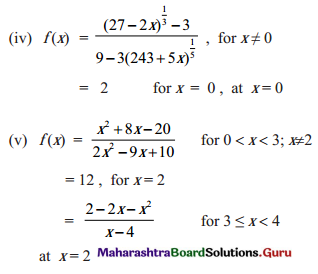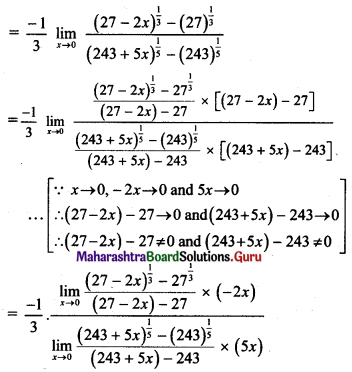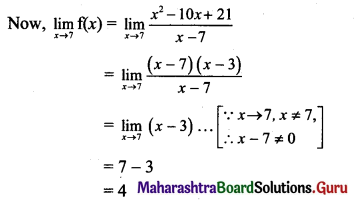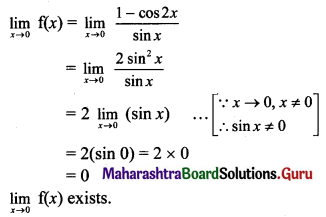Balbharti Maharashtra State Board 11th Maths Book Solutions Pdf Chapter 5 Sets and Relations Ex 5.1 Questions and Answers.

Maharashtra State Board 11th Maths Solutions Chapter 5 Sets and Relations Ex 5.1

Question 1.
Describe the following sets in Roster form:
(i) A = {x/x is a letter of the word ‘MOVEMENT’}
(ii) B = {x/x is an integer, –\(\frac{3}{2}\) < x < \(\frac{9}{2}\)>
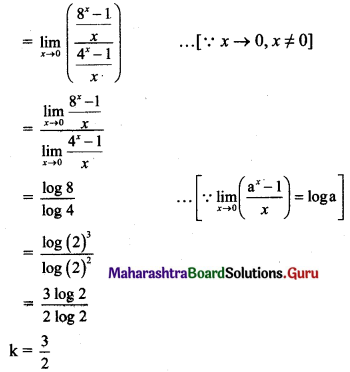
(iii) C = {x/x = 2n + 1, n ∈ N}
Solution:
(i) A = {M, O, V, E, N, T}
(ii) B = {-1, 0, 1, 2, 3, 4}
(iii) C = {3, 5, 7, 9, … }

Question 2.
Describe the following sets in Set-Builder form:
(i) {0}
(ii) {0, ±1, ±2, ±3}
(iii) \(\left\{\frac{1}{2}, \frac{2}{5}, \frac{3}{10}, \frac{4}{17}, \frac{5}{26}, \frac{6}{37}, \frac{7}{50}\right\}\)
(iv) {0, -1, 2, -3, 4, -5, 6,…}
Solution:
(i) Let A = {0}
0 is a whole number but it is not a natural number.
∴ A = {x / x ∈ W, x ∉ N}

(ii) Let B = {0, ±1, ±2, ±3}
B is the set of elements which belongs to Z from -3 to 3.
∴ B = {x /x ∈ Z, -3 ≤ x ≤ 3}

(iii) Let C = \(\left\{\frac{1}{2}, \frac{2}{5}, \frac{3}{10}, \frac{4}{17}, \frac{5}{26}, \frac{6}{37}, \frac{7}{50}\right\}\)
∴ C = {x / x = \(\frac{n}{n^{2}+1}\), n ∈ N, n ≤ 7}

(iv) Let D = {0, -1, 2, -3, 4, -5, 6, …}
∴ D = {x/x = (-1)n-1 × (n – 1), n ∈ N}

Question 3.
If A = {x / 6x² + x – 15 = 0}, B = {x / 2x² – 5x – 3 = 0}, C = {x / 2x² – x – 3 = 0}, then find
(i) (A ∪ B ∪ C)
(ii) (A ∩ B ∩ C)
Solution:
A = [x/6x² + x – 15 = 0)
6x² + x – 15 = 0
6x² + 10x – 9x – 15 = 0
2x(3x + 5) – 3(3x + 5) = 0
(3x + 5) (2x – 3) = 0
3x + 5 = 0 or 2x – 3 = 0
x = \(\frac{-5}{3}\) or x = \(\frac{3}{2}\)
A = {\(\frac{-5}{3}\), \(\frac{3}{2}\)}

B = {x/2x² – 5x – 3 = 0}
2x² – 5x – 3 = 0
2x² – 6x + x – 3 = 0
2x(x – 3) + 1(x – 3) = 0
(x – 3)(2x + 1) = 0
x – 3 = 0 or 2x + 1 = 0
x = 3 or x = \(\frac{-1}{2}\)
B = (\(\frac{-1}{2}\), 3)

C = {x/2x² – x – 3 = 0}
2x² – x – 3 = 0
2x² – 3x + 2x – 3 = 0
x(2x – 3) + 1(2x – 3) = 0
(2x – 3) (x + 1) = 0
2x – 3 = 0 or x + 1 = 0
x = \(\frac{3}{2}\) or x = -1
C = {-1, \(\frac{3}{2}\)}

(i) A ∪ B ∪ C = \(\left\{-\frac{5}{3}, \frac{3}{2}\right\} \cup\left\{\frac{-1}{2}, 3\right\} \cup\left\{-1, \frac{3}{2}\right\}\) = \(\left\{\frac{-5}{3},-1, \frac{-1}{2}, \frac{3}{2}, 3\right\}\)

(ii) A ∩ B ∩ C = { }

Question 4.
If A, B, C are the sets for the letters in the words ‘college’, ‘marriage’ and ‘luggage’ respectively, then verify that [A – (B ∪ C)] = [(A – B) ∩ (A – C)].
Solution:
A = {c, o, l, g, e}
B = {m, a, r, i, g, e}
C = {l, u, g, a, e}
B ∪ C = {m, a, r, i, g, e, l, u}
A – (B ∪ C) = {c, o}
A – B = {c, o, l}
A – C = {c, o}
∴ [(A – B) ∩ (A – C)] = {c, o} = A – (B ∪ C)
∴ [A -( B ∪ C)] = [(A – B) ∩ (A – C)]

Question 5.
If A = {1, 2, 3, 4}, B = {3, 4, 5, 6}, C = {4, 5, 6, 7, 8} and universal set X = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}, then verify the following:
(i) A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C)
(ii) A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C)
(iii) (A ∪ B)’ = A’ ∩ B’
(iv) (A ∩ B)’ = A’ ∪ B’
(v) A = (A ∩ B) ∪ (A ∩ B’)
(vi) B = (A ∩ B) ∪ (A’ ∩ B)
(vii) (A ∪ B) = (A – B) ∪ (A ∩ B) ∪ (B – A)
(viii) A ∩ (B ∆ C) = (A ∩ B) ∆ (A ∩ C)
(ix) n(A ∪ B) = n(A) + n(B) – n(A ∩ B)
(x) n(B) = n (A’ ∩ B) + n (A ∩ B)
Solution:
A = {1, 2, 3, 4}, B = {3, 4, 5, 6}, C = {4, 5, 6, 7, 8},
X = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
(i) B ∩ C = {4, 5, 6}
∴ A ∪ (B ∩ C) = {1, 2, 3, 4, 5, 6} …..(i)
A ∪ B = {1, 2, 3, 4, 5, 6}
A ∪ C = {1, 2, 3, 4, 5, 6, 7, 8}
∴ (A ∪ B) ∩ (A ∪ C) = {1, 2, 3, 4, 5, 6} …….(ii)
From (i) and (ii), we get
A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C)

(ii) B ∪ C = {3, 4, 5, 6, 7, 8}
∴ A ∩ (B ∪ C) = {3, 4} ………(i)
A ∩ B = {3, 4}
A ∩ C = {4}
∴ (A ∩ B) ∪ (A∩ C) = {3, 4} ……..(ii)
From (i) and (ii), we get
A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C)

(iii) A ∪ B = {1, 2, 3, 4, 5, 6}
∴ (A ∪ B)’ = {7, 8, 9, 10} ………(i)
A’ = {5, 6, 7, 8, 9, 10},
B’ = {1, 2, 7, 8, 9,10}
∴ A’ ∩ B’ = {7, 8, 9, 10} …….(ii)
From (i) and (ii), we get
(A ∪ B)’ = A’ ∩ B’

(iv) A ∩ B = {3, 4}
(A ∩ B)’= {1, 2, 5, 6, 7, 8, 9, 10} …….(i)
A’ = {5, 6, 7, 8, 9, 10}
B’ = {1, 2, 7, 8, 9, 10}
∴ A’ ∪ B’ = {1, 2, 5, 6, 7, 8, 9, 10} …….(ii)
From (i) and (ii), we get
(A ∩ B)’ = A’ ∪ B’

(v) A = {1, 2, 3, 4} ……(i)
A ∩ B = {3, 4}
B’ = {1, 2, 7, 8, 9, 10}
A ∩ B’ = {1, 2}
∴ (A ∩ B) ∪ (A ∩ B’) = {1, 2, 3, 4} …..(ii)
From (i) and (ii), we get
A = (A ∩ B) ∪ (A ∩ B’)

(vi) B = {3, 4, 5, 6} …..(i)
A ∩ B = {3, 4}
A’ = {5, 6, 7, 8, 9, 10}
A’ ∩ B = {5, 6}
∴ (A ∩ B) ∪ (A’ ∩ B) = {3, 4, 5, 6} …..(ii)
From (i) and (ii), we get
B = (A ∩ B) ∪ (A’ ∩ B)

(vii) A ∪ B = {1, 2, 3, 4, 5, 6} …….(i)
A – B = {1, 2}
A ∩ B = {3, 4}
B – A = {5, 6}
∴ (A – B) ∪ (A ∩ B) ∪ (B – A) = {1, 2, 3, 4, 5, 6} ……(ii)
From (i) and (ii), we get
A ∪ B = (A – B) ∪ (A ∩ B) ∪ (B – A)

(viii) B – C = {3}
C – B = {7, 8}
B Δ C = (B – C) ∪ (C – B) = {3, 7, 8}
∴ A ∩ (B Δ C) = {3} ……(i)
A ∩ B = {3, 4}
A ∩ C = {4}
∴ (A ∩ B) Δ (A ∩ C) = [(A ∩ B) – (A ∩ C)] ∪ [(A ∩ C) – (A ∩ B)] = {3} …..(ii)
From (i) and (ii), we get
A ∩ (B Δ C) = (A ∩ B) Δ (A ∩ C)

(ix) A = {1, 2, 3, 4}, B = {3, 4, 5, 6}
A ∩ B = {3, 4}, A ∪ B = {1, 2, 3, 4, 5, 6}
∴ n(A) = 4, n(B) = 4,
n(A ∩ B) = 2, n(A ∪ B) = 6 ……(i)
∴ n(A) + n(B) – n(A ∩ B) = 4 + 4 – 2
∴ n(A) + n(B) – n(A ∩ B) = 6 …..(ii)
From (i) and (ii), we get
n(A ∪ B) = n(A) + n(B) – n(A ∩ B)

(x) B = {3, 4, 5, 6}
∴ n(B) = 4 …..(i)
A’ = {5, 6, 7, 8, 9, 10}
A’ ∩ B = {5, 6}
∴ n(A’ ∩ B) = 2
A ∩ B = {3, 4}
∴ n(A ∩ B) = 2
∴ n(A’ ∩ B) + n(A ∩ B) = 2 + 2 = 4 …..(ii)
From (i) and (ii), we get
n(B) = n(A’ ∩ B) + n (A ∩ B)

Question 6.
If A and B are subsets of the universal set X and n(X) = 50, n(A) = 35, n(B) = 20, n(A’ ∩ B’) = 5, find
(i) n(A ∪ B)
(ii) n(A ∩ B)
(iii) n(A’ ∩ B)
(iv) n(A ∩ B’)
Solution:
n(X) = 50, n(A) = 35, n(B) = 20, n(A’ ∩ B’) = 5
(i) n(A ∪ B) = n(X) – [n(A ∪ B)’]
= n(X) – n(A’ ∩ B’)
= 50 – 5
= 45

(ii) n(A ∩ B) = n(A) + n(B) – n(A ∪ B)
= 35 + 20 – 45
= 10

(iii) n(A’ ∩ B) = n(B) – n(A ∩ B)
= 20 – 10
= 10

(iv) n(A ∩ B’) = n(A) – n(A ∩ B)
= 35 – 10
= 25

Question 7.
In a class of 200 students who appeared in certain examinations, 35 students faded in CET, 40 in NEET and 40 in JEE, 20 faded in CET and NEET, 17 in NEET and JEE, 15 in CET and JEE and 5 faded in ad three examinations. Find how many students
(i) did not fail in any examination.
(ii) faded in NEET or JEE entrance.
Solution:
Let A = set of students who failed in CET
B = set of students who failed in NEET
C = set of students who failed in JEE
X = set of all students
∴ n(X) = 200, n(A) = 35, n(B) = 40, n(C) = 40, n(A ∩ B) = 20, n(B ∩ C) = 17, n(A ∩ C) = 15, n(A ∩ B ∩ C) = 5

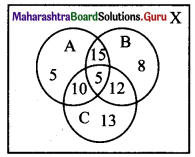
(i) n(A ∪ B ∪ C) = n(A) + n(B) + n(C) – n(A ∩ B) – n(B ∩ C) – n(A ∩ C) + n(A ∩ B ∩ C)
= 35 + 40 + 40 – 20 – 17 – 15 + 5
= 68
∴ No. of students who did not fail in any exam = n(X) – n(A ∪ B ∪ C)
= 200 – 68
= 132

(ii) No. of students who failed in NEET or JEE entrance = n(B ∪ C)
= n(B) + n(C) – n(B ∩ C)
= 40 + 40 – 17
= 63

Question 8.
From amongst 2000 Uterate individuals of a town, 70% read Marathi newspapers, 50% read English newspapers and 32.5% read both Marathi and English newspapers. Find the number of individuals who read
(i) at least one of the newspapers.
(ii) neither Marathi nor English newspaper.
(iii) only one of the newspapers.
Solution:
Let M = set of individuals who read Marathi newspapers
E = set of individuals who read English newspapers
X = set of all literate individuals
∴ n(X) = 2000,
n(M) = \(\frac{70}{100}\) × 2000 = 1400
n(E) = \(\frac{50}{100}\) × 2000 = 1000
n(M ∩ E) = \(\frac{32.5}{100}\) × 2000 = 650
(i) n(M ∪ E) = n(M) + n(E) – n(M ∩ E)
= 1400 + 1000 – 650
= 1750

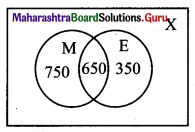
No. of individuals who read at least one of the newspapers = n(M ∪ E) = 1750.

(ii) No. of individuals who read neither Marathi nor English newspaper = n(M’ ∩ E’)
= n(M ∪ E)’
= n(X) – n(M ∪ E)
= 2000 – 1750
= 250

(iii) No. of individuals who read only one of the newspapers = n(M ∩ E’) + n(M’ ∩ E)
= n(M ∪ E) – n(M ∩ E)
= 1750 – 650
= 1100

Question 9.
In a hostel, 25 students take tea, 20 students take coffee, 15 students take milk, 10 students take both tea and coffee, 8 students take both milk and coffee. None of them take tea and milk both and everyone takes atleast one beverage, find the total number of students in the hostel.
Solution:
Let T = set of students who take tea
C = set of students who take coffee
M = set of students who take milk
∴ n(T) = 25, n(C) = 20, n(M) = 15, n(T ∩ C) = 10, n(M ∩ C) = 8, n(T ∩ M) = 0, n(T ∩ M ∩ C) = 0

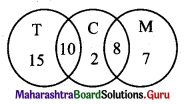
∴ Total number of students in the hostel = n(T ∪ C ∪ M)
= n(T) + n(C) + n(M) – n(T ∩ C) – n(M ∩ C) – n(T ∩ M) + n(T ∩ M ∩ C)
= 25 + 20 + 15 – 10 – 8 – 0 + 0
= 42

Question 10.
There are 260 persons with skin disorders. If 150 had been exposed to the chemical A, 74 to the chemical B, and 36 to both chemicals A and B, find the number of persons exposed to
(i) Chemical A but not Chemical B
(ii) Chemical B but not Chemical A
(iii) Chemical A or Chemical B
Solution:
Let A = set of persons exposed to chemical A
B = set of persons exposed to chemical B
X = set of all persons
∴ n(X) = 260, n(A) = 150, n(B) = 74, n(A ∩ B) = 36

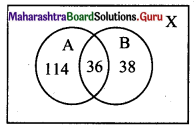
(i) No. of persons exposed to chemical A but not to chemical B = n(A ∩ B’)
= n(A) – n(A ∩ B)
= 150 – 36
= 114

(ii) No. of persons exposed to chemical B but not to chemical A = n(A’ ∩ B)
= n(B) – n(A ∩ B)
= 74 – 36
= 38

(iii) No. of persons exposed to chemical A or chemical B = n(A ∪ B)
= n(A) + n(B) – n(A ∩ B)
= 150 + 74 – 36
= 188

Question 11.
Write down the power set of A = {1, 2, 3}.
Solution:
A = {1, 2, 3}
The power set of A is given by
P(A) = {{Φ}, {2}, {3}, {1, 2}, {2, 3}, {1, 3}, {1, 2, 3}}

Question 12.
Write the following intervals in Set-Builder form:
(i) (-3, 0)
(ii) [6, 12]
(iii) (6, ∞)
(iv) (-∞, 5]
(v) (2, 5]
(vi) [-3, 4)
Solution:
(i) (-3, 0) = {x / x ∈ R, -3 < x < 0}

(ii) [6, 12] = {x / x ∈ R, 6 ≤ x ≤ 12}

(iii) (6, ∞) = {x / x ∈ R, x > 6}

(iv) (-∞, 5] = {x / x ∈ R, x ≤ 5}

(v) (2, 5] = {x / x ∈ R, 2 < x ≤ 5}

(vi) [-3, 4) = {x / x ∈ R, -3 ≤ x < 4}

Question 13.
A college awarded 38 medals in volleyball, 15 in football, and 20 in basketball. The medals were awarded to a total of 58 players and only 3 players got medals in all three sports. How many received medals in exactly two of the three sports?
Solution:
Let A = Set of students who received medals in volleyball
B = Set of students who received medals in football
C = Set of students who received medals in basketball
n(A) = 38, n(B) = 15, n(C) = 20, n(A ∪ B ∪ C) = 58, n(A ∩ B ∩ C) = 3
n(A ∪ B ∪ C) = n(A) + n(B) + n(C) – n(A ∩ B) – n(B ∩ C) – n(A ∩ C) + n(A ∩ B ∩ C)
58 = 38 + 15 + 20 – n(A ∩ B) – n(B ∩ C) – n(A ∩ C) + 3
∴ n(A ∩ B) + n(B ∩ C) + n(A ∩ C) = 18 ……(i)
Number of players who got exactly two medals = p + q + r
Here, s = n(A ∩ B ∩ C) = 3

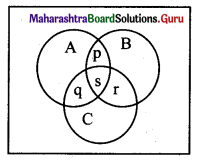
n(A ∩ B) + n(B ∩ C) + n(A ∩ C) = 18 …..[From (i)]
∴ p + s + s + r + q + s = 18
∴ p + q + r + 3s = 18
∴ p + q + r + 3(3) = 18
∴ p + q + r = 18 – 9 = 9
∴ Number of players who received exactly two medals = 9.

Question 14.
Solve the following inequalities and write the solution set using interval notation.
(i) -9 < 2x + 7 ≤ 19
(ii) x² – x > 20
(iii) \(\frac{2 x}{x-4}\) ≤ 5
(iv) 6x² + 1 ≤ 5x
Solution:
(i) -9 < 2x + 7 ≤ 19
∴ -16 < 2x ≤ 12
∴ -8< x ≤ 6
∴ x ∈ (-8, 6]

(ii) x² – x > 20
∴ x² – x – 20 > 0
∴ x² – 5x + 4x – 20 > 0
∴ (x – 5) (x + 4) > 0
∴ either x – 5 > 0 and x + 4 > 0 or x – 5 < 0 and x + 4 < 0

Case I: x – 5 > 0 and x + 4 > 0
∴ x > 5 and x > -4
∴ x > 5 ….(i)

Case II:
x – 5 < 0 and x + 4 < 0
∴ x < 5 and x < -4
∴ x < -4 …..(ii)
From (i) and (ii), we get
x ∈ (-∞, – 4) ∪ (5, ∞)

(iii) \(\frac{2 x}{x-4}\) ≤ 5
∴ \(\frac{2 x}{x-4}\) – 5 ≤ 0
∴ \(\frac{2 x-5 x+20}{x-4}\) ≤ 0
∴ \(\frac{20-3 x}{x-4}\) ≤ 0
When \(\frac{a}{b}\) ≤ 0,
a ≥ 0 and b < 0 or a ≤ 0 and b > 0
∴ either 20 – 3x ≥ 0 and x – 4 < 0 or 20 – 3x ≤ 0 and x – 4 > 0
Case I:
20 – 3x ≥ 0 and x – 4 < 0
∴ x ≤ \(\frac{20}{3}\) and x < 4
∴ x < 4 ……(I)

Case II: 20 – 3x ≤ 0 and x – 4 > 0
∴ x ≥ \(\frac{20}{3}\) and x > 4
∴ x ≥ \(\frac{20}{3}\) ……(ii)
From (i) and (ii), we get
x ∈ (-∞, 4) ∪ [\(\frac{20}{3}\), ∞)

(iv) 6x² + 1 ≤ 5x
6x² – 5x + 1 ≤ 0
6x² – 3x – 2x + 1 ≤ 0
(3x – 1) (2x – 1) ≤ 0
either 3x – 1 ≤ 0 and 2x – 1 ≥ 0 or 3x – 1 ≥ 0 and 2x – 1 ≤ 0
Case I:
3x – 1 ≤ 0 and 2x – 1 ≥ 0
∴ x ≤ \(\frac{1}{3}\) and x ≥ \(\frac{1}{2}\), which is not possible.

Case II:
3x – 1 ≥ 0 and 2x – 1 ≤ 0
∴ x ≥ \(\frac{1}{3}\) and x ≤ \(\frac{1}{2}\)
∴ x ∈ [\(\frac{1}{3}\), \(\frac{1}{2}\)]

Question 15.
If A = (-7, 3], B = [2, 6] and C = [4, 9], then find
(i) A ∪ B
(ii) B ∪ C
(iii) A ∪ C
(iv) A ∩ B
(v) B ∩ C
(vi) A ∩ C
(vii) A’ ∩ B
(viii) B’ ∩ C’
(ix) B – C
(x) A – B
Solution:
A = (-7, 3], B = [2, 6], C = [4, 9]
(i) A ∪ B = (-7, 6]

(ii) B ∪ C = [2, 9]

(iii) A ∪ C = (-7, 3] ∪ [4, 9]

(iv) A ∩ B = [2, 3]

(v) B ∩ C = [4, 6]

(vi) A ∩ C = { }

(vii) A’ = (-∞, – 7] ∪ (3, ∞)
∴ A’ ∩ B = (3, 6]

(viii) B’ = (-∞, 2) ∪ (6, ∞)
C’ = (-∞, 4) ∪ (9, ∞)
∴ B’ ∩ C’ = (-∞, 2) ∪ (9, ∞)

(ix) B – C = [2, 4)

(x) A – B = (-7, 2)

Balbharti Maharashtra State Board 11th Maths Book Solutions Pdf Chapter 2 Sequences and Series Ex 2.2 Questions and Answers.

Maharashtra State Board 11th Maths Solutions Chapter 2 Sequences and Series Ex 2.2

Question 1.
For the following G.P.s, find S_n.
(i) 3, 6, 12, 24, ……..
Solution:

(ii) p, q, \(\frac{\mathbf{q}^{2}}{\mathbf{p}}, \frac{\mathbf{q}^{3}}{\mathbf{p}^{2}}, \ldots\)
Solution:

(iii) 0.7, 0.07, 0.007, …….
Solution:

(iv) √5, -5, 5√5, -25, …….
Solution:

Question 2.
For a G.P.
(i) a = 2, r = \(-\frac{2}{3}\), find S₆.
Solution:

(ii) If S₅ = 1023, r = 4, find a.
Solution:

Question 3.
For a G.P.
(i) If a = 2, r = 3, S_n = 242, find n.
Solution:

(ii) For a G.P. sum of the first 3 terms is 125 and the sum of the next 3 terms is 27, find the value of r.
Solution:

Question 4.
For a G.P.
(i) If t₃ = 20, t₆ = 160, find S₇.
Solution:

(ii) If t₄ = 16, t₉ = 512, find S₁₀.
Solution:

Question 5.
Find the sum to n terms
(i) 3 + 33 + 333 + 3333 + …..
Solution:
S_n = 3 + 33 + 333 +….. upto n terms
= 3(1 + 11 + 111 +….. upto n terms)
= \(\frac{3}{9}\)(9 + 99 + 999 + ….. upto n terms)
= \(\frac{3}{9}\)[(10 – 1) + (100 – 1) + (1000 – 1) +… upto n terms]
= \(\frac{3}{9}\)[(10 + 100 + 1000 + … upto nterms) – (1 + 1 + 1 + ….. n times)]
But 10, 100, 1000, ….. n terms are in G.P. with
a = 10, r = \(\frac{100}{10}\) = 10

(ii) 8 + 88 + 888 + 8888 + …..
Solution:
S_n = 8 + 88 + 888 + … upto n terms
= 8(1 + 11 + 111 + … upto n terms)
= \(\frac{8}{9}\)(9 + 99 + 999 + … upto n terms)
= \(\frac{8}{9}\)[(10 – 1) + (100 – 1) + (1000 – 1) +… upto n terms]
= \(\frac{8}{9}\)[(10 + 100 + 1000 + … upto n terms) – (1 + 1 + 1 + … n times)]
But 10, 100, 1000, … n terms are in G.P. with
a = 10, r = \(\frac{100}{10}\) = 10

Question 6.
Find the sum to n terms
(i) 0.4 + 0.44 + 0.444 + …..
Solution:
S_n = 0.4 + 0.44 + 0.444 + ….. upto n terms
= 4(0.1 + 0.11 +0.111 + …. upto n terms)
= \(\frac{4}{9}\)(0.9 + 0.99 + 0.999 + … upto n terms)
= \(\frac{4}{9}\)[(1 – 0.1) + (1 – 0.01) + (1 – 0.001) … upto n terms]
= \(\frac{4}{9}\)[(1 + 1 + 1 + …n times) – (0.1 + 0.01 + 0.001 +… upto n terms)]
But 0.1, 0.01, 0.001, … n terms are in G.P. with
a = 0.1, r = \(\frac{0.01}{0.1}\) = 0.1

(ii) 0.7 + 0.77 + 0.777 + ……
Solution:
S_n = 0.7 + 0.77 + 0.777 + … upto n terms
= 7(0.1 + 0.11 + 0.111 + … upton terms)
= \(\frac{7}{9}\)(0.9 + 0.99 + 0.999 + … upto n terms)
= \(\frac{7}{9}\)[(1 – 0.1) + (1 – 0.01) + (1 – 0.001) +… upto n terms]
= \(\frac{7}{9}\)[(1 + 1 + 1 +… n times) – (0.1 + 0.01 + 0.001 +… upto n terms )]
But 0.1, 0.01, 0.001, … n terms are in G.P. with
a = 0.1, r = \(\frac{0.01}{0.1}\) = 0.1

Question 7.
Find the sum to n terms of the sequence
(i) 0.5, 0.05, 0.005, …..
Solution:

(ii) 0.2, 0.02, 0.002, ……
Solution:

Question 8.
For a sequence, if S_n = 2(3n – 1), find the nth term, hence showing that the sequence is a G.P.
Solution:

Question 9.
If S, P, R are the sum, product, and sum of the reciprocals of n terms of a G.P, respectively, then verify that \(\left[\frac{S}{R}\right]^{n}\) = P².
Solution:
Let a be the 1st term and r be the common ratio of the G.P.
∴ the G.P. is a, ar, ar², ar³, …, ar^n-1

Question 10.
If S_n, S_2n, S_3n are the sum of n, 2n, 3n terms of a G.P. respectively, then verify that S_n(S_3n – S_2n) = (S_2n – S_n)².
Solution:
Let a and r be the 1st term and common ratio of the G.P. respectively.

Question 11.
Find
(i) \(\sum_{r=1}^{10}\left(3 \times 2^{r}\right)\)
Solution:

(ii) \(\sum_{r=1}^{10} 5 \times 3^{r}\)
Solution:

Question 12.
The value of a house appreciates 5% per year. How much is the house worth after 6 years if its current worth is Rs. 15 Lac. [Given: (1.05)⁵ = 1.28, (1.05)⁶ = 1.34]
Solution:
The value of a house is Rs. 15 Lac.
Appreciation rate = 5% = \(\frac{5}{100}\) = 0.05
Value of house after 1st year = 15(1 + 0.05) = 15(1.05)
Value of house after 6 years = 15(1.05) (1.05)⁵
= 15(1.05)⁶
= 15(1.34)
= 20.1 lac.

Question 13.
If one invests Rs. 10,000 in a bank at a rate of interest 8% per annum, how long does it take to double the money by compound interest? [(1.08)⁵ = 1.47]
Solution:
Amount invested = Rs. 10000
Interest rate = \(\frac{8}{100}\) = 0.08
amount after 1st year = 10000(1 + 0.08) = 10000(1.08)
Value of the amount after n years
= 10000(1.08) × (1.08)^n-1
= 10000(1.08)ⁿ
= 20000
∴ (1.08)ⁿ = 2
∴ (1.08)⁵ = 1.47 …..[Given]
∴ n = 10 years, (approximately)

Balbharti Maharashtra State Board 11th Maths Book Solutions Pdf Chapter 8 Continuity Ex 8.1 Questions and Answers.

Maharashtra State Board 11th Maths Solutions Chapter 8 Continuity Ex 8.1

Question 1.
Examine the continuity of
(i) f(x) = x³ + 2x² – x – 2 at x = -2
Solution:
Given, f(x) = x³ + 2x² – x – 2
f(x) is a polynomial function and hence it is continuous for all x ∈ R.
∴ f(x) is continuous at x = -2.

(ii) f(x) = sin x, for x ≤ \(\frac{\pi}{4}\)
= cos x, for x > \(\frac{\pi}{4}\), at x = \(\frac{\pi}{4}\)
Solution:

(iii) f(x) = \(\frac{x^{2}-9}{x-3}\), for x ≠ 3
= 8 for x = 3, at x = 3.
Solution:
f(3) = 8 ….(given)

∴ f(x) is discontinuous at x = 3.

Question 2.
Examine whether the function is continuous at the points indicated against them.
(i) f(x) = x³ – 2x + 1, if x ≤ 2
= 3x – 2, if x > 2, at x = 2.
Solution:

(ii) f(x) = \(\frac{x^{2}+18 x-19}{x-1}\), for x ≠ 1
= 20, for x = 1, at x = 1.
Solution:

(iii) f(x) = \(\frac{x}{\tan 3 x}+2\), for x < 0
= \(\frac{7}{3}\), for x ≥ 0, at x = 0.
Solution:

Question 3.
Find all the points of discontinuities of f(x) = [x] on the interval (-3, 2).
Solution:
f(x) = [x], x ∈ (-3, 2)
i.e., f(x) = -3, x ∈ (-3, -2)
= -2, x ∈ [-2, -1)
= -1, x ∈ [- 1, 0)
= 0, x ∈ [0, 1)
= 1, x ∈ [1, 2)

Similarly, f(x) is discontinuous at the points x = -1, x = 0, x = 1.
Thus all the integer values of x in the interval (-3, 2),
i.e., the points x = -2, x = -1, x = 0 and x = 1 are the required points of discontinuities.

Question 4.
Discuss the continuity of the function f(x) = |2x + 3|, at x = \(\frac{-3}{2}\).
Solution:

Question 5.
Test the continuity of the following functions at the points or intervals indicated against them.


Solution:

Question 6.
Identify discontinuities for the following functions as either a jump or a removable discontinuity.
(i) f(x) = \(\frac{x^{2}-10 x+21}{x-7}\)
Solution:
Given, f(x) = \(\frac{x^{2}-10 x+21}{x-7}\)
It is a rational function and is discontinuous if
x – 7 = 0, i.e., x = 7
∴ f(x) is continuous for all x ∈ R, except at x = 7.
∴ f(7) is not defined.

Thus, \(\lim _{x \rightarrow 7} \mathrm{f}(x)\) exist but f(7) is not defined.
∴ f(x) has a removable discontinuity.

(ii) f(x) = x² + 3x – 2, for x ≤ 4
= 5x + 3, for x > 4.
Solution:
f(x) = x² + 3x – 2, x ≤ 4
= 5x + 3, x > 4
f(x) is a polynomial function for both the intervals.
∴ f(x) is continuous for both the given intervals.
Let us test the continuity at x = 4.

∴ f(x) is discontinuous at x = 4.
∴ f(x) has a jump discontinuity at x = 4.

(iii) f(x) = x² – 3x – 2, for x < -3 = 3 + 8x, for x > -3.
Solution:
f(x) = x² – 3x – 2, x < -3 = 3 + 8x, x > -3
f(x) is a polynomial function for both the intervals.
∴ f(x) is continuous for both the given intervals.
Let us test the continuity at x = -3.

∴ f(x) is discontinuous at x = -3.
∴ f(x) has a jump discontinuity at x = -3

(iv) f(x) = 4 + sin x, for x < π = 3 – cos x for x > π.
Solution:
f(x) = 4 + sin x, x < π = 3 – cos x, x > π
sin x and cos x are continuous for all x ∈ R.
4 and 3 are constant functions.
∴ 4 + sin x and 3 – cos x are continuous for all x ∈ R.
∴ f(x) is continuous for both the given intervals.
Let us test the continuity at x = π.

But f(π) is not defined.
∴ f(x) has a removable discontinuity at x = π.

Question 7.
Show that the following functions have a continuous extension to the point where f(x) is not defined. Also, find the extension.
(i) f(x) = \(\frac{1-\cos 2 x}{\sin x}\), for x ≠ 0.
Solution:
f(x) = \(\frac{1-\cos 2 x}{\sin x}\), for x ≠ 0
Here, f(0) is not defined.
Consider,

But f(0) is not defined.
∴ f(x) has a removable discontinuity at x = 0.
∴ The extension of the original function is
f(x) = \(\frac{1-\cos 2 x}{\sin x}\) for x ≠ 0
= 0 for x = 0
∴ f(x) is continuous at x = 0.

(ii) f(x) = \(\frac{3 \sin ^{2} x+2 \cos x(1-\cos 2 x)}{2\left(1-\cos ^{2} x\right)}\), for x ≠ 0.
Solution:
f(x) = \(\frac{3 \sin ^{2} x+2 \cos x(1-\cos 2 x)}{2\left(1-\cos ^{2} x\right)}\), for x ≠ 0
Here, f(0) is not defined.
Consider,

But f(0) is not defined.
∴ f(x) has a removable discontinuity at x = 0.
∴ The extension of the original function is
f(x) = \(\frac{3 \sin ^{2} x+2 \cos x(1-\cos 2 x)}{2\left(1-\cos ^{2} x\right)}\), x ≠ 0
= \(\frac{7}{2}\), x = 0
∴ f(x) is continuous at x = 0.

(iii) f(x) = \(\frac{x^{2}-1}{x^{3}+1}\), for x ≠ -1
Solution:
f(x) = \(\frac{x^{2}-1}{x^{3}+1}\), for x ≠ -1
Here, f(-1) is not defined.
Consider,

But f(-1) is not defined.
∴ f(x) has a removable discontinuity at x = -1.
∴ The extension of the original function is
f(x) = \(\frac{x^{2}-1}{x^{3}+1}\), x ≠ -1
= \(-\frac{2}{3}\), x = -1
∴ f(x) is continuous at x = \(-\frac{2}{3}\)

Question 8.
Discuss the continuity of the following functions at the points indicated against them.

Solution:

Question 9.
Which of the following functions has a removable discontinuity? If it has a removable discontinuity, redefine the function so that it becomes continuous.


Solution:

Question 10.
(i) If f(x) = \(\frac{\sqrt{2+\sin x}-\sqrt{3}}{\cos ^{2} x}\), for x ≠ \(\frac{\pi}{2}\), is continuous at x = \(\frac{\pi}{2}\) then find f(\(\frac{\pi}{2}\)).
Solution:
f(x) is continuous at x = \(\frac{\pi}{2}\), …..(given)

(ii) If f(x) = \(\frac{\cos ^{2} x-\sin ^{2} x-1}{\sqrt{3 x^{2}+1}-1}\) for x ≠ 0, is continuous at x = 0 then find f(0).
Solution:
f(x) is continuous at x = 0, …..(given)

(iii) If f(x) = \(\frac{4^{x-\pi}+4^{\pi-x}-2}{(x-\pi)^{2}}\) for x ≠ π, is continuous at x = π, then find f(π).
Solution:
f(x) is continuous at x = π, …..(given)

Question 11.
(i) If f(x) = \(\frac{24^{x}-8^{x}-3^{x}+1}{12^{x}-4^{x}-3^{x}+1}\), for x ≠ 0
= k, for x = 0
is continuous at x = 0, then find k.
Solution:
f(x) is continuous at x = 0 …..(given)

(ii) If f(x) = \(\frac{5^{x}+5^{-x}-2}{x^{2}}\), for x ≠ 0
= k, for x = 0
is continuous at x = 0, then find k.
Solution:
f(x) is continuous at x = 0 …..(given)

(iii) If f(x) = \(\frac{\sin 2 x}{5 x}\) – a, for x > 0
= 4 for x = 0
= x² + b – 3, for x < 0
is continuous at x = 0, find a and b.
Solution:
f(x) is continuous at x = 0 ……(given)

(iv) For what values of a and b is the function
f(x) = ax + 2b + 18, for x ≤ 0
= x² + 3a – b, for 0 < x ≤ 2 = 8x – 2, for x > 2,
continuous for every x?
Solution:
f(x) is continuous for every x …..(given)
∴ f(x) is continuous at x = 0 and x = 2.
As f(x) is continuous at x = 0,
\(\lim _{x \rightarrow 0^{-}} \mathrm{f}(x)=\lim _{x \rightarrow 0^{+}} \mathrm{f}(x)\)

∴ (2)² + 3a – b = 8(2) – 2
∴ 4 + 3a – b = 14
∴ 3a – b = 10 …….(ii)
Subtracting (i) from (ii), we get
2a = 4
∴ a = 2
Substituting a = 2 in (i), we get
2 – b = 6
∴ b = -4
∴ a = 2 and b = -4

(v) For what values of a and b is the function
f(x) = \(\frac{x^{2}-4}{x-2}\), for x < 2
= ax² – bx + 3, for 2 ≤ x < 3
= 2x – a + b, for x ≥ 3
continuous for every x on R?
Solution:
f(x) is continuous for every x on R …..(given)
∴ f(x) is continuous at x = 2 and x = 3.
As f(x) is continuous at x = 2,

∴ a(3)² – b(3) + 3 = 2(3) – a + b
∴ 9a – 3b + 3 = 6 – a + b
∴ 10a – 4b = 3 …..(ii)
Multiplying (i) by 2, we get
8a – 4b = 2 ….(iii)
Subtracting (ii) from (iii), we get
-2a = -1
∴ a = \(\frac{1}{2}\)
Substituting a = \(\frac{1}{2}\) in (i), we get
4(\(\frac{1}{2}\)) – 2b = 1
∴ 2 – 2b = 1
∴ 1 = 2b
∴ b = \(\frac{1}{2}\)
∴ a = \(\frac{1}{2}\) and b = \(\frac{1}{2}\)

Question 12.
Discuss the continuity of f on its domain, where
f(x) = |x + 1|, for -3 ≤ x ≤ 2
= |x – 5|, for 2 < x ≤ 7
Solution:

Question 13.
Discuss the continuity of f(x) at x = \(\frac{\pi}{4}\) where,
f(x) = \(\frac{(\sin x+\cos x)^{3}-2 \sqrt{2}}{\sin 2 x-1}\), for x ≠ \(\frac{\pi}{4}\)
= \(\frac{3}{\sqrt{2}}\), for x = \(\frac{\pi}{4}\)
Solution:

Question 14.
Determine the values of p and q such that the following function is continuous on the entire real number line.
f(x) = x + 1, for 1 < x < 3
= x² + px + q, for |x – 2| ≥ 1.
Solution:
|x – 2| ≥ 1
∴ x – 2 ≥ 1 or x – 2 ≤ -1
∴ x ≥ 3 or x ≤ 1
∴ f(x) = x² + px + q for x ≥ 3 as well as x ≤ 1
Thus, f(x) = x² + px + q; x ≤ 1
= x + 1; 1 < x < 3 = x² + px + q; x > 3
f(x) is continuous for all x ∈ R.
∴ f(x) is continuous at x = 1 and x = 3.
As f(x) is continuous at x = 1,

Subtracting (i) from (ii), we get
2p = -6
∴ p = -3
Substituting p = -3 in (i), we get
-3 + q = 1
∴ q = 4
∴ p = -3 and q = 4

Question 15.
Show that there is a root for the equation 2x³ – x – 16 = 0 between 2 and 3.
Solution:
Let f(x) = 2x³ – x – 16
f(x) is a polynomial function and hence it is continuous for all x ∈ R.
A root of f(x) exists, if f(x) = 0 for at least one value of x.
f(2) = 2(2)³ – 2 – 16 = -2 < 0
f(3) = 2(3)³ – 3 – 16 = 35 > 0
∴ f(2) < 0 and f(3) > 0
∴ By intermediate value theorem,
there has to be point ‘c’ between 2 and 3 such that f(c) = 0.
∴ There is a root of the given equation between 2 and 3.

Question 16.
Show that there is a root for the equation x³ – 3x = 0 between 1 and 2.
Solution:
Let f(x) = x³ – 3x
f(x) is a polynomial function and hence it is continuous for all x ∈ R.
A root of f(x) exists, if f(x) = 0 for at least one value of x.
f(1) = (1)³ – 3(1) = -2 < 0
f(2) = (2)³ – 3(2) = 2 > 0
∴ f(1) < 0 and f(2) > 0
∴ By intermediate value theorem,
there has to be point ‘c’ between 1 and 2 such that f(c) = 0.
There is a root of the given equation between 1 and 2.

Question 17.
Let f(x) = ax + b (where a and b are unknown)
= x² + 5 for x ∈ R
Find the values of a and b, so that f(x) is continuous at x = 1.

Solution:
f(x) = x² + 5, x ∈ R
∴ f(1) = 1 + 5 = 6
If f(x) = ax + b is continuous at x = 1, then
f(1) = \(\lim _{x \rightarrow 1}(a x+b)\) = a + b
∴ 6 = a + b where, a, b ∈ R
∴ There are infinitely many values of a and b.

Question 18.
Activity: Suppose f(x) = px + 3 for a ≤ x ≤ b
= 5x² – q for b < x ≤ c
Find the condition on p, q, so that f(x) is continuous on [a, c], by filling in the boxes.

Solution:

Balbharti Maharashtra State Board 11th Maths Book Solutions Pdf Chapter 9 Differentiation Ex 9.2 Questions and Answers.

Maharashtra State Board 11th Maths Solutions Chapter 9 Differentiation Ex 9.2

(I) Differentiate the following w.r.t. x

Question 1.
y = \(x^{\frac{4}{3}}+e^{x}-\sin x\)
Solution:

Question 2.
y = √x + tan x – x³
Solution:

Question 3.
y = log x – cosec x + \(5^{x}-\frac{3}{x^{\frac{3}{2}}}\)
Solution:

Question 4.
y = \(x^{\frac{7}{3}}+5 x^{\frac{4}{5}}-\frac{5}{x^{\frac{2}{5}}}\)
Solution:

Question 5.
y = 7^x + x⁷ – \(\frac{2}{3}\) x√x – log x + 7⁷
Solution:

Question 6.
y = 3 cot x – 5e^x + 3 log x – \(\frac{4}{x^{\frac{3}{4}}}\)
Solution:

(II) Diffrentiate the following w.r.t. x

Question 1.
y = x⁵ tan x
Solution:

Question 2.
y = x³ log x
Solution:

Question 3.
y = (x² + 2)² sin x
Solution:

Question 4.
y = e^x log x
Solution:

Question 5.
y = \(x^{\frac{3}{2}} e^{x} \log x\)
Solution:

Question 6.
y = \(\log e^{x^{3}} \log x^{3}\)
Solution:

(III) Diffrentiate the following w.r.t. x

Question 1.
y = x²√x + x⁴ log x
Solution:

Question 2.
y = e^x sec x – \(x^{\frac{5}{3}}\) log x
Solution:

Question 3.
y = x⁴ + x√x cos x – x² e^x
Solution:

Question 4.
y = (x³ – 2) tan x – x cos x + 7^x . x⁷
Solution:

Question 5.
y = sin x log x + e^x cos x – e^x √x
Solution:

Question 6.
y = e^x tan x + cos x log x – √x 5^x
Solution:

(IV) Diffrentiate the following w.r.t.x.

Question 1.
y = \(\frac{x^{2}+3}{x^{2}-5}\)
Solution:

Question 2.
y = \(\frac{\sqrt{x}+5}{\sqrt{x}-5}\)
Solution:

Question 3.
y = \(\frac{x e^{x}}{x+e^{x}}\)
Solution:

Question 4.
y = \(\frac{x \log x}{x+\log x}\)
Solution:
y = \(\frac{x \log x}{x+\log x}\)

Question 5.
y = \(\frac{x^{2} \sin x}{x+\cos x}\)
Solution:

Question 6.
y = \(\frac{5 e^{x}-4}{3 e^{x}-2}\)
Solution:

(V).

Question 1.
If f(x) is a quadratic polynomial such that f(0) = 3, f'(2) = 2 and f'(3) = 12, then find f(x).
Solution:
Let f(x) = ax² + bx + c …..(i)
∴ f(0) = a(0)² + b(0) + c
∴ f(0) = c
But, f(0) = 3 …..(given)
∴ c = 3 …..(ii)
Differentiating (i) w.r.t. x, we get
f'(x) = 2ax + b
∴ f'(2) = 2a(2) + b
∴ f'(2) = 4a + b
But, f'(2) = 2 …..(given)
∴ 4a + b = 2 …..(iii)
Also, f'(3) = 2a(3) + b
∴ f'(3) = 6a + b
But, f'(3) = 12 …..(given)
∴ 6a + b = 12 …..(iv)
equation (iv) – equation (iii), we get
2a = 10
∴ a = 5
Substituting a = 5 in (iii), we get
4(5) + b = 2
∴ b = -18
∴ a = 5, b = -18, c = 3
∴ f(x) = 5x² – 18x + 3

Check:
If f(0) = 3, f'(2) = 2 and f'(3) = 12, then our answer is correct.
f(x) = 5x² – 18x + 3 and f'(x) = 10x – 18
f(0) = 5(0)² – 18(0) + 3 = 3
f'(2) = 10(2) – 18 = 2
f'(3) = 10(3) – 18 = 12
Thus, our answer is correct.

Question 2.
If f(x) = a sin x – b cos x, f'(\(\frac{\pi}{4}\)) = √2 and f'(\(\frac{\pi}{6}\)) = 2, then find f(x).
Solution:
f(x) = a sin x – b cos x
Differentiating w.r.t. x, we get
f'(x) = a cos x – b (- sin x)
∴ f'(x) = a cos x + b sin x


Now, f(x) = a sin x – b cos x
∴ f(x) = (√3 + 1) sin x + (√3 – 1) cos x

VI. Fill in the blanks. (Activity Problems)

Question 1.
y = e^x . tan x
Diff. w.r.t. x

Solution:

Question 2.
y = \(\frac{\sin x}{x^{2}+2}\)
diff. w.r.t. x

Solution:

Question 3.
y = (3x² + 5) cos x
Diff. w.r.t. x

Solution:

Question 4.
Differentiate tan x and sec x w.r.t. x using the formulae for differentiation of \(\frac{u}{v}\) and \(\frac{1}{v}\) respectively.
Solution:

Balbharti Maharashtra State Board 11th Maths Book Solutions Pdf Chapter 2 Sequences and Series Ex 2.1 Questions and Answers.

Maharashtra State Board 11th Maths Solutions Chapter 2 Sequences and Series Ex 2.1

Question 1.
Check whether the following sequences are G.P. If so, write t_n.
(i) 2, 6, 18, 54, ……
Solution:

(ii) 1, -5, 25, -125, ………
Solution:

(iii) \(\sqrt{5}, \frac{1}{\sqrt{5}}, \frac{1}{5 \sqrt{5}}, \frac{1}{25 \sqrt{5}}, \cdots\)
Solution:

(iv) 3, 4, 5, 6, ……
Solution:

(v) 7, 14, 21, 28, ……
Solution:

Question 2.
For the G.P.
(i) If r = \(\frac{1}{3}\), a = 9, find t₇.
Solution:

(ii) If a = \(\frac{7}{243}\), r = 3, find t₆.
Solution:

(iii) If r = -3 and t₆ = 1701, find a.
Solution:

(iv) If a = \(\frac{2}{3}\), t₆ = 162, find r.
Solution:

Question 3.
Which term of the G. P. 5, 25, 125, 625, …… is 5¹⁰?
Solution:

Question 4.
For what values of x, the terms \(\frac{4}{3}\), x, \(\frac{4}{27}\) are in G. P.?
Solution:

Question 5.
If for a sequence, \(\mathrm{t}_{\mathrm{n}}=\frac{5^{n-3}}{2^{n-3}}\), show that the sequence is a G. P. Find its first term and the common ratio.
Solution:

Question 6.
Find three numbers in G. P. such that their sum is 21 and the sum of their squares is 189.
Solution:
Let the three numbers in G. P. be \(\frac{a}{r}\), a, ar.
According to the given conditions,


When a = 6, r = 2,
\(\frac{a}{r}\) = 3, a = 6, ar = 12
Hence, the three numbers in G.P. are 12, 6, 3 or 3, 6, 12.

Check:
If sum of the three numbers is 21 and sum of their squares is 189, then our answer is correct.
Sum of the numbers = 12 + 6 + 3 = 21
Sum of the squares of the numbers = 12² + 6² + 3²
= 144 + 36 + 9
= 189
Thus, our answer is correct.

Question 7.
Find four numbers in G. P. such that the sum of the middle two numbers is \(\frac{10}{3}\) and their product is 1.
Solution:
Let the four numbers in G.P. be \(\frac{a}{r^{3}}, \frac{a}{r}, a r, a r^{3}\)
According to the given conditions,

Question 8.
Find five numbers in G. P. such that their product is 1024 and the fifth term is square of the third term.
Solution:
Let the five numbers in G. P. be
\(\frac{a}{r^{2}}, \frac{a}{r}, a, a r, a r^{2}\)
According to the given conditions,

Hence, the five numbers in G.P. are
1, 2, 4, 8, 16 or 1, -2, 4, -8, 16.

Question 9.
The fifth term of a G. P. is x, the eighth term of a G.P. is y and the eleventh term of a G.P. is z, verify whether y² = xz.
Solution:

Question 10.
If p, q, r, s are in G.P., show that p + q, q + r, r + s are also in G. P.
Solution:
p, q, r, s are in G.P.
∴ \(\frac{\mathrm{q}}{\mathrm{p}}=\frac{\mathrm{r}}{\mathrm{q}}=\frac{\mathrm{s}}{\mathrm{r}}\)
Let \(\frac{\mathrm{q}}{\mathrm{p}}=\frac{\mathrm{r}}{\mathrm{q}}=\frac{\mathrm{s}}{\mathrm{r}}\) = k
∴ q = pk, r = qk, s = rk
We have to prove that p + q, q + r, r + s are in G.P.
i.e., to prove that \(\frac{\mathrm{q}+\mathrm{r}}{\mathrm{p}+\mathrm{q}}=\frac{\mathrm{r}+\mathrm{s}}{\mathrm{q}+\mathrm{r}}\)

∴ p + q, q + r, r + s are in G.P.

Question 11.
The number of bacteria in a culture doubles every hour. If there were 50 bacteria originally in the culture, how many bacteria will be there at the end of the 5th hour?
Solution:
Since the number of bacteria in culture doubles every hour, increase in number of bacteria after every hour is in G.P.
∴ a = 50, r = \(\frac{100}{50}\) = 2
t_n = ar^n-1
To find the number of bacteria at the end of the 5th hour.
(i.e., to find the number of bacteria at the beginning of the 6th hour, i.e., to find t₆.)
∴ t₆ = ar⁵
= 50 × (2⁵)
= 50 × 32
= 1600

Question 12.
A ball is dropped from a height of 80 ft. The ball is such that it rebounds \(\left(\frac{3}{4}\right)^{\text {th }}\) of the height it has fallen. How high does the ball rebound on the 6th bounce? How high does the ball rebound on the nth bounce?
Solution:
Since the ball rebounds \(\left(\frac{3}{4}\right)^{\text {th }}\) of the height it has fallen, the height in successive bounce is in G.P.
1st height in the bounce = 80 × \(\frac{3}{4}\)

Question 13.
The numbers 3, x and x + 6 are in G. P. Find
(i) x
(ii) 20th term
(iii) nth term.
Solution:
(i) 3, x and x + 6 are in G. P.
\(\frac{x}{3}=\frac{x+6}{x}\)
x² = 3x + 18
x² – 3x – 18 = 0
(x – 6) (x + 3) = 0
x = 6, -3

Question 14.
Mosquitoes are growing at a rate of 10% a year. If there were 200 mosquitoes in the beginning, write down the number of mosquitoes after
(i) 3 years
(ii) 10 years
(iii) n years
Solution:
a = 200, r = 1 + \(\frac{10}{100}\) = \(\frac{11}{10}\)
Mosquitoes at the end of 1st year = 200 × \(\frac{11}{10}\)
(i) Number of mosquitoes after 3 years
= 200 × \(\frac{11}{10} \times\left(\frac{11}{10}\right)^{2}\)
= 200 \(\left(\frac{11}{10}\right)^{3}\)
= 200 (1.1)³

(ii) Number of mosquitoes after 10 years = 200 (1.1)¹⁰

(iii) Number of mosquitoes after n years = 200 (1.1)ⁿ

Question 15.
The numbers x – 6, 2x and x² are in G. P. Find
(i) x
(ii) 1st term
(iii) nth term
Solution:
(i) x – 6, 2x and x are in Geometric progression.
∴ \(\frac{2 x}{x-6}=\frac{x^{2}}{2 x}\)
4x² = x²(x – 6)
4 = x – 6
x = 10

(ii) t₁ = x – 6 = 10 – 6 = 4