Prasanna

Balbharti Maharashtra State Board Class 8 Maths Solutions covers the Practice Set 2.3 8th Std Maths Answers Solutions Chapter 2 Parallel Lines and Transversals.

Practice Set 2.3 8th Std Maths Answers Chapter 2 Parallel Lines and Transversals

Question 1.
Draw a line l. Take a point A outside the line. Through point A draw a line parallel to line l.
Solution:
Steps of construction:

1. Draw a line l and take any point A outside the line.
2. Place a set-square, such that one arm of the right angle passes through A and the other arm is on line l.
3. Place the second set-square as shown in the figure such that the vertex of the right angle is at point A.
4. Hold the two set-squares in place and draw a line parallel to line l through the edge of the second set-square. Name the line as m.

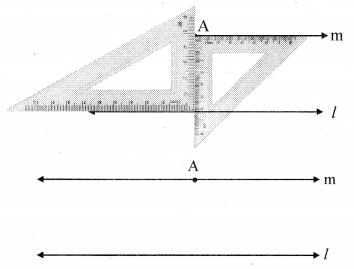
Line m is the required line parallel to line l and passing through point A.

Question 2.
Draw a line l. Take a point T outside the line. Through point T draw a line parallel to line l.
Solution:
Steps of construction:

1. Draw a line l and take any point T outside the line.
2. Place a set-square, such that one arm of the right angle passes through T and the other arm is on line l.
3. Place the second set-square as shown in the figure such that the vertex of the right angle is at point T.
4. Hold the two set-squares in place and draw a line parallel to line l through the edge of the second set-square. Name the line as m.

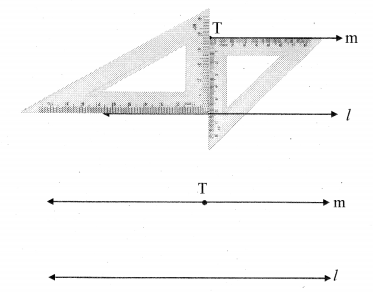
Line m is the required line parallel to line l and passing through point T.

Question 3.
Draw a line m. Draw a line n which is parallel to line m at a distance of 4 cm from it.
Solution:
Steps of construction:

1. Draw a line m and take any two points M and N on the line.
2. Draw perpendiculars to line m at points M and N.
3. On the perpendicular lines take points S and T at a distance 4 cm from points M and N respectively.
4. Draw a line through points S and T. Name the line as n.

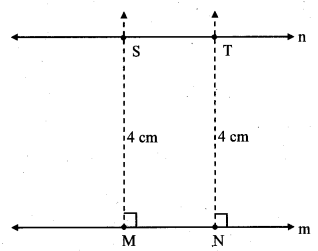
Line n is parallel to line m at a distance of 4 cm from it.

Balbharti Maharashtra State Board Class 8 Maths Solutions covers the Practice Set 2.1 8th Std Maths Answers Solutions Chapter 2 Parallel Lines and Transversals.

Practice Set 2.1 8th Std Maths Answers Chapter 2 Parallel Lines and Transversals

Question 1.
In the given figure, each angle is shown by a letter. Fill in the boxes with the help of the figure

Corresponding angles:
i. ∠p and __
ii. ∠q and __
iii. ∠r and __
iv. ∠s and __

Interior alternate angles:
v. ∠s and __
vi. ∠w and __
Solution:
i. ∠w
ii. ∠x
iii. ∠y
iv. ∠z
v. ∠x
vi. ∠r

Question 2.
Observe the angles shown in the figure and write the following pair of angles.

1. Interior alternate angles
2. Corresponding angles
3. Interior angles

Solution:

1. ∠c and ∠e; ∠b and ∠h
2. ∠a and ∠e; ∠b and ∠f; ∠c and ∠g; ∠d and ∠h
3. ∠c and ∠h; ∠b and ∠e

Balbharti Maharashtra State Board Class 8 Maths Solutions covers the Practice Set 1.3 8th Std Maths Answers Solutions Chapter 1 Rational and Irrational Numbers.

Practice Set 1.3 8th Std Maths Answers Chapter 1 Rational and Irrational Numbers

Question 1.
Write the following rational numbers in decimal form.
i. \(\frac { 9 }{ 37 }\)
ii. \(\frac { 18 }{ 42 }\)
iii. \(\frac { 9 }{ 14 }\)
iv. \(-\frac { 103 }{ 5 }\)
v. \(-\frac { 11 }{ 13 }\)
Solution:
i. \(\frac { 9 }{ 37 }\)

ii. \(\frac { 18 }{ 42 }\)

iii. \(\frac { 9 }{ 14 }\)

iv. \(-\frac { 103 }{ 5 }\)

v. \(-\frac { 11 }{ 13 }\)

Balbharti Maharashtra State Board Class 8 Maths Solutions covers the Practice Set 1.2 8th Std Maths Answers Solutions Chapter 1 Rational and Irrational Numbers.

Practice Set 1.2 8th Std Maths Answers Chapter 1 Rational and Irrational Numbers

Question 1.
Compare the following numbers.
i. 7, -2
ii. 0, \(\frac { -9 }{ 5 }\)
iii. \(\frac { 8 }{ 7 }\), 0
iv. \(-\frac{5}{4}, \frac{1}{4}\)
v. \(\frac{40}{29}, \frac{141}{29}\)
vi. \(-\frac{17}{20},-\frac{13}{20}\)
vii. \(\frac{15}{12}, \frac{7}{16}\)
viii. \(-\frac{25}{8},-\frac{9}{4}\)
ix. \(\frac{12}{15}, \frac{3}{5}\)
x. \(-\frac{7}{11},-\frac{3}{4}\)
Solution:
i. 7, -2
If a and b are positive numbers such that a < b, then -a > -b.
Since, 2 < 7 ∴ -2 > -7

ii. 0, \(\frac { -9 }{ 5 }\)
On a number line, \(\frac { -9 }{ 5 }\) is to the left of zero.
∴ 0 > \(\frac { -9 }{ 5 }\)

iii. \(\frac { 8 }{ 7 }\), 0
On a number line, zero is to the left of \(\frac { 8 }{ 7 }\) .
∴ \(\frac { 8 }{ 7 }\) > 0

iv. \(-\frac{5}{4}, \frac{1}{4}\)
We know that, a negative number is always less than a positive number.
∴ \(-\frac{5}{4}<\frac{1}{4}\)

v. \(\frac{40}{29}, \frac{141}{29}\)
Here, the denominators of the given numbers are the same.
Since, 40 < 141
∴ \(\frac{40}{29}<\frac{141}{29}\)

vi. \(-\frac{17}{20},-\frac{13}{20}\)
Here, the denominators of the given numbers are the same.
Since, 17 < 13
∴ -17 < -13
∴ \(-\frac{17}{20}<-\frac{13}{20}\)

vii. \(\frac{15}{12}, \frac{7}{16}\)
Here, the denominators of the given numbers are not the same.
LCM of 12 and 16 = 48

Alternate method:
15 × 16 = 240
12 × 7 = 84
Since, 240 > 84
∴ 15 × 16 > 12 × 7

viii. \(-\frac{25}{8},-\frac{9}{4}\)
Here, the denominators of the given numbers are not the same.
LCM of 8 and 4 = 8

ix. \(\frac{12}{15}, \frac{3}{5}\)
Here, the denominators of the given numbers are not the same.
LCM of 15 and 5 = 15

x. \(-\frac{7}{11},-\frac{3}{4}\)
Here, the denominators of the given numbers are not the same.
LCM of 11 and 4 = 44

Maharashtra Board Class 8 Maths Solutions Chapter 1 Rational and Irrational Numbers Practice Set 1.2 Questions and Activities

Question 1.
Verify the following comparisons using a number line. (Textbook pg. no, .3)
i. 2 < 3 but – 2 > – 3
ii. \(\frac{5}{4}<\frac{7}{4}\) but \(\frac{-5}{4}<\frac{-7}{4}\)
Solution:

We know that, on a number line the number to the left is smaller than the other.
∴ 2 < 3 and -3 < -2
i.e. 2 < 3 and -2 > -3

Balbharti Maharashtra State Board Class 8 Maths Solutions covers the Practice Set 17.2 8th Std Maths Answers Solutions Chapter 17 Circle: Chord and Arc.

Practice Set 17.2 8th Std Maths Answers Chapter 17 Circle: Chord and Arc

Question 1.
The diameters PQ and RS of the circle with centre C are perpendicular to each other at C. State, why arc PS and arc SQ are congruent. Write the other arcs which are congruent to arc PS.

Solution:
diameter PQ ⊥ diameter RS … [Given]
∴ m∠PCS = m∠SCQ = m∠PCR = m∠RCQ = 90°
The measure of the angle subtended at the centre by an arc is the measure of the arc.
∴ m(arc PS) = m∠PCS = 90° …(i)
m (arc SQ) = m∠SCQ = 90° …(ii)
∴ m(arc PS) = m(arc SQ) … [From (i) and (ii)]
∴ arc PS ≅ arc SQ … [If the measures of two arcs of a circle are same, then the two arcs are congruent]
m(arc PR) = m∠PCR = 90° .. .(iii)
m (arc RQ) = m∠RCQ = 90° … (iv)
∴ m(arc PS) = m(arc PR) = m(arc RQ) … [From (i), (iii) and (iv)]
∴ arc PS ≅ arc PR ≅ arc RQ
… [If the measures of two arcs of a circle are same, then the two arcs are congruent]
∴ arc PR and arc RQ are congruent to arc PS.

Question 2.
In the given figure, O is the centre of the circle whose diameter is MN. Measures of some central angles are given in the figure.
i. m∠AOB and m∠COD
ii. Show that arc AB ≅ arc CD
iii. Show that chord AB ≅ chord CD

Solution:
i. Seg MN is the diameter of the circle. … [Given]
∴ m∠AOM + m∠AON = 180° … [Angles in a linear pair]
∴ m∠AOM + (m∠AOB + m∠BON) = 180° … [Angle addition property]
∴ 100° + m∠AOB + 35° = 180°
…[∵ m∠AOM = 100°, m∠BON = 35°]
∴ m∠AOB + 135° = 180°
∴ m∠AOB = 180°- 135°
∴m∠AOB = 45° …(i)
Also, m∠DOM + m∠DON = 180° … [Angles in a linear pair]
∴ m∠DOM + (m∠COD + m∠CON) = 180° … [Angle addition property]
∴ 100° +m∠COD + 35°= 180°
…[∵ m∠DOM = 100°, m∠CON = 35° ]
∴ m∠COD + 135° = 180°
∴ m∠COD = 180°- 135°
∴ m∠COD = 45° …(ii)

ii. m(arc AB) = m∠AOB = 45° … [From (i)]
m(arc DC) = m∠DOC = 45° .. .[From (ii)]
∴ m(arc AB) = m(arc DC) …[From (i) and (ii)]
∴ arc AB ≅ arc CD
… [If the measures of two arcs of a circle are same, then the two arcs are congruent]

iii. arc AB ≅ arc CD
∴ chord AB ≅ chord CD ….[The chords corresponding to congruent arcs are congruent]

Maharashtra Board Class 8 Maths Chapter 17 Circle: Chord and Arc Practice Set 17.2 Intext Questions and Activities

Question 1.
If the measures of two arcs of a circle are same, then two arcs are congruent. Verify this property using tracing paper. (Textbook pg. no. 117)
Solution:
[Students should attempt the above activities on their own.]

Question 2.
With the help of following activity find out the properties of the chord and the corresponding arc.
i. a. Draw a circle with centre O.
b. Draw ∠COD and ∠AOB of same measure.
You will find that the arc AXB and arc CYD are congruent.
c. Draw chords AB and CD.
d. Using compass experience that the length of chord AB and chord CD is also same.
(Textbook pg. no. 117)

Solution:
[Students should attempt the above activities on their own.]

ii. a. Draw a circle with centre C.
b. Draw the congruent chords AB and DE of the circle. Draw the radii CA, CB, CD and CE.
c. Check that ∠ACB and ∠DCE are congruent.
d. Hence show that measure of arc AB and arc DE is equal. Hence these arcs are congruent. (Textbook pg. no. 117)

Solution:
[Students should attempt the above activities on their own.]

Balbharti Maharashtra State Board Class 8 Maths Solutions covers the Practice Set 16.3 8th Std Maths Answers Solutions Chapter 16 Surface Area and Volume.

Practice Set 16.3 8th Std Maths Answers Chapter 16 Surface Area and Volume

Question 1.
Find the volume of the cylinder if height (h) and radius of the base (r) are as given below.
i. r = 10.5 cm, h = 8 cm
ii. r = 2.5 m, h = 7 m
iii. r = 4.2 cm, h = 5 cm
iv. r = 5.6 cm, h = 5 cm
Solution:
i. Given: r = 10.5 cm and h = 8 cm
To find: Volume of the cylinder
Volume of the cylinder = πr²h
= \(\frac { 22 }{ 7 }\) x 10.5 x 10.5 x 8
= 22 x 1.5 x 10.5 x 8
= 2772 cc
∴ The volume of the cylinder is 2772 cc.

ii. Given: r = 2.5 m and h = 7 m
To find: Volume of the cylinder
Volume of the cylinder = πr²h
= \(\frac { 22 }{ 7 }\) x 2.5 x 2.5 x 7
= 22 x 2.5 x 2.5
= 137.5 cu.m
∴ The volume of the cylinder is 137.5 cu.m.

iii. Given: r = 4.2 cm and h = 5 cm
To find: Volume of the cylinder
Volume of the cylinder = πr²h
= \(\frac { 22 }{ 7 }\) x 4.2 x 4.2 x 5
= 22 x 0.6 x 4.2 x 5
= 277.2 cc
∴ The volume of the cylinder is 277.2 cc.

iv. Given: r = 5.6 cm and h = 5 cm
To find: Volume of the cylinder
Volume of the cylinder = πr²h
= \(\frac { 22 }{ 7 }\) x 5.6 x 5.6 X 5 7
= 22 x 0.8 x 5.6 x 5
= 492.8 cc
∴ The volume of the cylinder is 492.8 cc.

Question 2.
How much iron is needed to make a rod of length 90 cm and diameter 1.4 cm?
Solution:
Given: For cylindrical rod: length of rod (h) = 90 cm, and
diameter (d) = 1.4 cm
To find: Iron required to make a rod
diameter (d) = 1.4 cm
∴ radius (r) = \(\frac{\mathrm{d}}{2}=\frac{1.4}{2}\) = 0.7 cm
Volume of rod = πr²h
= \(\frac { 22 }{ 7 }\) x 0.7 x 0.7 x 90
= 22 x 0.1 x 0.7 x 90
= 138.60 cc
∴ 138.60 cc of iron is required to make the rod.

Question 3.
How much water will a tank hold if the interior diameter of the tank is 1.6 m and its depth is 0.7 m?
Solution:
Given: interior diameter of the tank (d) = 1.6 m
and depth (h) = 0.7 m
To find: Capacity of the tank
interior diameter of the tank (d) = 1.6 m
∴ Interior radius (r) = \(\frac{\mathrm{d}}{2}=\frac{1.6}{2}\)
= 0.8 m
= 0.8 x 100
…[∵ 1m = 100cm]
= 80cm
h = 0.7 m = 0.7 x 100 = 70 cm
Capacity of the tank = Volume of the tank = πr²h
= \(\frac { 22 }{ 7 }\) x 80 x 80 x 70
= 22 x 80 x 80 x 10
= 1408000 cc
= \(\frac { 1408000 }{ 1000 }\)
…[∵1 litre = 1000 cc]
= 1408 litre
∴The tank can hold 1408 litre of water.

Question 4.
Find the volume of the cylinder if the circumference of the base of cylinder is 132 cm and height is 25 cm.
Solution:
Given: Circumference of the base of cylinder = 132 cm and height (h) = 25 cm
To find: Volume of the cylinder
i. Circumference of base of cylinder = 2πr
∴132 = 2 x \(\frac { 22 }{ 7 }\) x r
∴\(\frac{132 \times 7}{2 \times 22}=r\)
∴\(\frac{6 \times 7}{2}=r\)
∴3 x 7 = r
∴r = 21 cm

ii. Volume of the cylinder = πr²h
= \(\frac { 22 }{ 7 }\) x 21 x 21 x 25
= 22 x 3 x 21 x 25
= 34650 cc
∴ The volume of the cylinder is 34650 cc.

Maharashtra Board Class 8 Maths Chapter 16 Surface Area and Volume Practice Set 16.3 Intext Questions and Activities

Question 1.
Leonard Euler, discovered an interesting formula regarding the faces, vertices and edges of solid figures.
Count and write the faces, vertices and edges of the following figures and complete the table. From the table verify Euler’s formula, F + V = E + 2. (Textbook pg. No. 113)

Solution:

From the above table, F + V = E + 2 i.e. Euler’s formula is verified.

Balbharti Maharashtra State Board Class 8 Maths Solutions covers the Practice Set 16.2 8th Std Maths Answers Solutions Chapter 16 Surface Area and Volume.

Practice Set 16.2 8th Std Maths Answers Chapter 16 Surface Area and Volume

Question 1.
In each example given below, radius of base of a cylinder and its height are given. Then find the curved surface area and total surface area.
i. r = 7 cm, h = 10 cm
ii. r = 1.4 cm, h = 2.1 cm
iii. r = 2.5 cm, h = 7 cm
iv. r = 70 cm, h = 1.4 cm
v. r = 4.2 cm, h = 14 cm
Solution:
i. Given: r = 7 cm and h = 10 cm
To find: Curved surface area of cylinder and total surface area
Curved surface area of the cylinder = 2πrh
= 2 x \(\frac { 22 }{ 7 }\) x 7 x 10
= 2 x 22 x 10
= 440 sq.cm
Total surface area of the cylinder:
= 2πr(h + r)
= 2 x \(\frac { 22 }{ 7 }\) x 7(10 + 7)
= 2 x \(\frac { 22 }{ 7 }\) x 7 x 17
= 2 x 22 x 17
= 748 sq.cm
The curved surface area of the cylinder is 440 sq.cm and its total surface area is 748 sq.cm.

ii. Given: r = 1.4 cm and h = 2.1 cm
To find: Curved surface area of cylinder and total surface area
Curved surface area of the cylinder = 2πrh
= 2 x \(\frac { 22 }{ 7 }\) x 1.4 x 2.1
= 2 x 22 x 0.2 x 2.1
= 18.48 sq.cm
Total surface area of the cylinder = 2πr (h + r)
= 2 x \(\frac { 22 }{ 7 }\) x 1.4 (2.1 + 1.4)
= 2 x \(\frac { 22 }{ 7 }\) x 1.4 x 3.5
= 2 x 22 x 0.2 x 3.5
= 30.80 sq.cm
∴ The curved surface area of the cylinder is 18.48 sq.cm and its total surface area is 30.80 sq.cm.

iii. Given: r = 2.5 cm and h = 7 cm
To find: Curved surface area of cylinder and total surface area
Curved surface area of the cylinder = 2πrh
= 2 x \(\frac { 22 }{ 7 }\) x 2.5 x 7
= 2 x 22 x 2.5
= 110 sq.cm
Total surface area of the cylinder = 2πr(h + r)
= 2 x \(\frac { 22 }{ 7 }\) x 2.5 (7+ 2.5)
= 2 x \(\frac { 22 }{ 7 }\) x 2.5 x 9.5
= \(\frac { 1045 }{ 7 }\)
= 149.29 sq.cm
∴ The curved surface area of the cylinder is 110 sq.cm and its total surface area is 149.29 sq.cm.

iv. Given: r = 70 cm and h = 1.4 cm
To find: Curved surface area of cylinder and total surface area
Curved surface area of the cylinder = 2πrh
= 2 x \(\frac { 22 }{ 7 }\) x 70 x 1.4
= 2 x 22 x 10 x 1.4
= 616 sq.cm
Total surface area of the cylinder = 2πr(h + r)
= 2 x \(\frac { 22 }{ 7 }\) x 70(1.4 + 70)
= 2 x \(\frac { 22 }{ 7 }\) x 70 x 71.4
= 2 x 22 x 10 x 71.4
= 2 x 22 x 714
= 31416 sq.cm
∴ The curved surface area of the cylinder is 616 sq.cm and its total surface area is 31416 sq.cm.

v. Given: r = 4.2 cm and h = 14 cm
To find: Curved surface area of cylinder and total surface area
Curved surface area of the cylinder = 2πrh
= 2 x \(\frac { 22 }{ 7 }\) x 4.2 x 14 = 2 x 22 x 4.2 x 2
= 369.60 sq.cm
Total surface area of the cylinder = 2πr (h + r)
= 2 x \(\frac { 22 }{ 7 }\) x 4.2 (14+ 4.2)
= 2 x \(\frac { 22 }{ 7 }\) x 4.2 x 18.2
= 2 x 22 x 0.6 x 18.2
= 480.48 sq.cm
∴ The curved surface area of the cylinder is 369.60 sq.cm and its total surface area is 480.48 sq.cm.

Question 2.
Find the total surface area of a closed cylindrical drum if its diameter is 50 cm and height is 45 cm. (π = 3.14)
Given: For cylindrical drum:
Diameter (d) = 50 cm
and height (h) = 45 cm
To find: Total surface area of the cylindrical drum
Solution:
Diameter (d) = 50 cm
∴ radius (r) = \(\frac{\mathrm{d}}{2}=\frac{50}{2}\) = 25 cm
Total surface area of the cylindrical drum = 2πr (h + r)
= 2 x 3.14 x 25 (45 + 25)
= 2 x 3.14 x 25 x 70
= 10,990 sq.cm
∴ The total surface area of the cylindrical drum is 10,990 sq.cm.

Question 3.
Find the area of base and radius of a cylinder if its curved surface area is 660 sq.cm and height is 21 cm.
Given: Curved surface area = 660 sq.cm, and height = 21 cm
To find: area of base and radius of a cylinder
Solution:
i. Curved surface area of cylinder = 2πrh
∴ 660 = 2 x \(\frac { 22 }{ 7 }\) x r x 21
∴ 660 = 2 x 22 x r x 3
∴ \(\frac{660}{2 \times 22 \times 3}=r\)
∴ \(\frac{660}{2 \times 66}=r\)
∴ 5 = r
i.e., r = 5 cm

ii. Area of a base of the cylinder = πr²
= \(\frac { 22 }{ 7 }\) x 5 x 5
= \(\frac { 550 }{ 7 }\)
= 78.57 sq.cm
∴The radius of the cylinder is 5 cm and the area of its base is 78.57 sq.cm.

Question 4.
Find the area of the sheet required to make a cylindrical container which is open at one side and whose diameter is 28 cm and height is 20 cm. Find the approximate area of the sheet required to make a lid of height 2 cm for this container.
Given: For cylindrical container:
diameter (d) = 28 cm, height (h₁) = 20 cm
For cylindrical lid: height (h₂) = 2 cm
To find: i. Surface area of the cylinder with one side open
ii. Area of sheet required to made a lid
Solution:
diameter (d) = 28 cm
∴ radius (r) = \(\frac{\mathrm{d}}{2}=\frac{28}{2}\) = 14 cm
i. Surface area of the cylinder with one side open = Curved surface area + Area of a base
= 2πrh₁ + πr²
= πr (2h₁ + r)
= \(\frac { 22 }{ 7 }\) x 14 x (2 x 20 + 14)
= 22 x 2 x (40 + 14)
= 22 x 2 x 54
= 2376 sq.cm

ii. Area of sheet required to made a lid = Curved surface area of lid + Area of upper surface
= 2πrh₂ + πr²
= πr (2h₂ + r)
= \(\frac { 22 }{ 7 }\) x 14 x (2 x 2 + 14)
= 22 x 2 x (4 + 14)
= 22 x 2 x 18
= 792 sq cm
∴ The area of the sheet required to make the cylindrical container is 2376 sq. cm and the approximate area of a sheet required to make the lid is 792 sq. cm.

Balbharti Maharashtra State Board Class 8 Maths Solutions covers the Practice Set 16.1 8th Std Maths Answers Solutions Chapter 16 Surface Area and Volume.

Practice Set 16.1 8th Std Maths Answers Chapter 16 Surface Area and Volume

Question 1.
Find the volume of a box if its length, breadth and height are 20 cm, 10.5 cm and 8 cm respectively.
Given: For cuboid shaped box,
length (l) = 20 cm, breadth (b) = 10.5 cm and height (h) = 8cm
To find: Volume of a box
Solution:
Volume of a box = l x b x h
= 20 x 10.5 x 8
= 1680 cc
∴ The volume of the box is 1680 cc.

Question 2.
A cuboid shaped soap bar has volume 150 cc. Find its thickness if its length is 10 cm and breadth is 5 cm.
Given: For cuboid shaped soap bar,
length (l) = 10 cm, breadth (b) = 5 cm and volume = 150 cc
To find: Thickness of the soap bar (h)
Solution:
Volume of soap bar = l x b x h
∴ 150 = 10 x 5 x h
∴ 150 = 50h
∴ \(\frac { 150 }{ 50 }=h\)
∴ 3 = h
i.e., h = 3 cm
∴ The thickness of the soap bar is 3 cm.

Question 3.
How many bricks of length 25 cm, breadth 15 cm and height 10 cm are required to build a wall of length 6 m, height 2.5 m and breadth 0.5 m?
Given: For the cuboidal shape brick:
length (l₁) = 25 cm,
breadth (b₁) = 15 cm,
height (h₁) = 10 cm
For the cuboidal shape wall:
length (l₂) = 6 m,
height (h₂) = 2.5 m,
breadth (b₂) = 0.5 m
To find: Number of bricks required
Solution:
When all the bricks are arranged to build a wall, the volume of all the bricks is equal to volume of wall.
∴ \(\text { Number of bricks }=\frac{\text { volume of the wall }}{\text { volume of a brick }}\)

i. Volume of a brick = l₁ x b₁ x h₁
= 25 x 15 x 10 cc

ii. l₂ = 6m = 6 x 100 …[∵ 1m = 100cm]
= 600 cm
h₂ = 2.5 m = 2.5 x 100 = 250 cm
b₂ = 0.5 m = 0.5 x 100 = 50 cm
Volume of the wall = l₂ x b₂ x h₂
= 600 x 50 x 250 cc

iii. \(\text { Number of bricks }=\frac{\text { volume of the wall }}{\text { volume of a brick }}\)
= \(\frac{600 \times 50 \times 250}{25 \times 15 \times 10}\)
= 40 x 2 x 25
= 2000 bricks
∴ 2000 bricks are required to build the wall.

Question 4.
For rain water harvesting a tank of length 10 m, breadth 6 m and depth 3 m is built. What is the capacity of the tank? How many litre of water can it hold?
Given: For a cuboidal tank,
Length (l) = 10 m, breadth (b) = 6 m, depth (h) = 3 m
To find: Capacity of the tank and litre of water tank can hold.
Solution:
i. l = 10m = 10 x 100 …[∵ 1m = 100cm]
= 1000 cm,
b = 6 m = 6 x 100 = 600 cm,
h = 3 m = 3 x 100 = 300 cm
Volume of the tank = l x b x h
= 1000 x 600 x 300
= 18,00,00,000 cc

ii. Capacity of the tank = Volume of the tank
= 18,00,00,000 cc
= \(\frac{18,00,00,000}{1000}\)
…[∵ 1 litre =1000 cc]
= 1,80,000 litre
∴ The capacity of the tank is 18,00,00,000 cc and it can hold 1,80,000 litre of water.

Balbharti Maharashtra State Board Class 8 Maths Solutions covers the Practice Set 15.6 8th Std Maths Answers Solutions Chapter 15 Area.

Practice Set 15.6 8th Std Maths Answers Chapter 15 Area

Question 1.
Radii of the circles are given below, find their areas.
i. 28 cm
ii. 10.5 cm
iii. 17.5 cm
Solution:
i. Radius of the circle (r) = 28 cm … [Given]
Area of the circle = πr²
= \(\frac { 22 }{ 7 }\) x (28)²
= \(\frac { 22 }{ 7 }\) x 28 x 28
= 22 x 4 x 28
= 2464 sq. cm

ii. Radius of the circle (r) = 10.5 cm … [Given]
Area of the circle = πr²
= \(\frac { 22 }{ 7 }\) x (10.5)²
= \(\frac { 22 }{ 7 }\) x 10.5 x 10.5
= 22 x 1.5 x 10.5
= 346.5 sq. cm

iii. Radius of the circle (r) = 17.5 cm … [Given]
Area of the circle = πr²
= \(\frac { 22 }{ 7 }\) x(17.5)²
= \(\frac { 22 }{ 7 }\) x 17.5 x 17.5
= 22 x 2.5 x 17.5
= 962.5 sq. cm

Question 2.
Areas of some circles are given below, find their diameters.
i. 176 sq.cm
ii. 394.24 sq. cm
iii. 12474 sq. cm
Solution:
i. Area of the circle =176 sq. cm .. .[Given]
Area of the circle = πr²
∴ 176 = \(\frac { 22 }{ 7 }\) x r²
∴ r² = 176 x \(\frac { 7 }{ 22 }\)
∴ r² = 56
∴ r = √56 … [Taking square root of both sides]
Diameter = 2r = 2√56 CM

ii. Area of the circle = 394.24 sq. cm … [Given]
Area of the circle = πr²

∴ Diameter = 2r = 2 x 11.2 = 22.4 cm

iii. Area of the circle = 12474 sq. cm …[Given]
Area of the circle = πr²
∴ 12474 = \(\frac { 22 }{ 7 }\) x r²
∴ r² = 12474 x \(\frac { 7 }{ 22 }\)
∴ r² = 567 x 7
∴ r² = 3969
∴ r = 63 …[Taking square root of both sides]
∴ Diameter = 2r = 2 x 63 = 126cm

Question 3.
Diameter of the circular garden is 42 m. There is a 3.5 m wide road around the garden. Find the area of the road.

Solution:

Diameter of the circular garden is 42 m. … [Given]
∴ Radius of the circular garden (r) = \(\frac { 42 }{ 2 }\) = 21 m
Width of the road = 3.5 m …[Given]
Radius of the outer circle (R)
= radius (r) + width of the road
= 21 + 3.5
= 24.5 m
Area of the road = area of outer circle – area of circular garden
= πR² – πr²
= π (R² – r²)
= \(\frac { 22 }{ 7 }\) [(24.5)² – (21)²]
= \(\frac { 22 }{ 7 }\) (24.5 + 21) (24.5 – 21)
…..[∵ a²-b² = (a+b)(a-b)]
= \(\frac { 22 }{ 7 }\) x 45.5 x 3.5
= 22 x 45.5 x 0.5
= 500.50 sq. m
∴ The area of the road is 500.50 sq. m.

Question 4.
Find the area of the circle if its circumference is 88 cm.
Solution:
Circumference of the circle = 88 cm …[Given]
Circumference of the circle = 2πr
∴ 88 = 2 x \(\frac { 22 }{ 7 }\) x r
∴ \(r=\frac{88 \times 7}{2 \times 22}\) ∴ r = 14cm
Area of the circle = πr² = \(\frac { 22 }{ 7 }\) x (14)²
= \(\frac { 22 }{ 7 }\) x 14 x 14 = 22 x 2 x 14 = 616 sq. cm
∴ The area of circle is 616 Sq cm

Maharashtra Board Class 8 Maths Chapter 15 Area Practice Set 15.6 Intext Questions and Activities

Question 1.
Draw a circle of radius 28mm. Draw any one triangle and draw a trapezium on the graph paper. Find the area of these figures by counting the number of small squares on the graph paper. Verify your answers using formula for area of these figures.
Observe that smaller the squares of graph paper, better is the approximation of area. (Textbook pg. no. 105)
Solution:
(Students should do this activity on their own.)

Balbharti Maharashtra State Board Class 8 Maths Solutions covers the Practice Set 15.5 8th Std Maths Answers Solutions Chapter 15 Area.

Practice Set 15.5 8th Std Maths Answers Chapter 15 Area

Question 1.
Find the areas of given plots. (All measures are in meters.)

Solution:
i. Here, ∆QAP, ∆RCS are right angled triangles and ☐QACR is a trapezium.
In ∆QAP, l(AP) = 30 m, l(QA) = 50 m
A(∆QAP)
= \(\frac { 1 }{ 2 }\) x product of sides forming the right angle
= \(\frac { 1 }{ 2 }\) x l(AP) x l(QA)
= \(\frac { 1 }{ 2 }\) x 30 x 50
= 750 sq. m
In ☐QACR, l(QA) = 50 m, l(RC) = 25 m,
l(AC) = l(AB) + l(BC)
= 30 + 30 = 60 m
A(☐QACR)
= \(\frac { 1 }{ 2 }\) x sum of lengths of parallel sides x height
= \(\frac { 1 }{ 2 }\) x [l(QA) + l(RC)] x l(AC)
= \(\frac { 1 }{ 2 }\) x (50 + 25) x 60
= \(\frac { 1 }{ 2 }\) x 75 x 60
= 2250 sq.m
In ∆RCS, l(CS) = 60 m, l(RC) = 25 m A(∆RCS)
= \(\frac { 1 }{ 2 }\) x product of sides forming the right angle
= \(\frac { 1 }{ 2 }\) x l(CS) x l(RC)
= \(\frac { 1 }{ 2 }\) x 60 x 25
= 750 sq. m
In ∆PTS, l(TB) = 30 m,
l(PS) = l(PA) + l(AB) + l(BC) + l(CS)
= 30 + 30 + 30 + 60
= 150m
A(∆PTS) = \(\frac { 1 }{ 2 }\) x base x height
= \(\frac { 1 }{ 2 }\) x l(PS) x l(TB)
= \(\frac { 1 }{ 2 }\) x 150 x 30
= 2250 sq. m
∴ Area of plot QPTSR = A(∆QAP) + A(☐QACR) + A(∆RCS) + A(∆PTS)
= 750 + 2250 + 750 + 2250
= 6000 sq. m
∴ The area of the given plot is 6000 sq.m.

ii. In ∆ABE, m∠BAE = 90°, l(AB) = 24 m, l(BE) = 30 m
∴ [l(BE)]² = [l(AB)]² + [l(AE)]²
…[Pythagoras theorem]
∴ (30)² = (24)² + [l(AE)]²
∴ 900 = 576 + [l(AE)]²
∴ [l(AE)]² = 900 – 576
∴ [l(AE)]² = 324
∴ l(AE) = √324 = 18 m
…[Taking square root of both sides]
A(∆ABE)
= \(\frac { 1 }{ 2 }\) x product of sides forming the right angle
= \(\frac { 1 }{ 2 }\) x l(AE) x l(AB)
= \(\frac { 1 }{ 2 }\) x 18 x 24
= 216 sq. m
In ∆BCE, a = 30m, b = 28m, c = 26m

∴ Area of plot ABCDE
= A(∆ABE) + A(∆BCE) + A(∆EDC)
= 216 + 336 + 224
= 776 sq. m
∴ The area of the given plot is 776 sq.m.
[Note: In the given figure, we have taken l(DF) = 16 m]