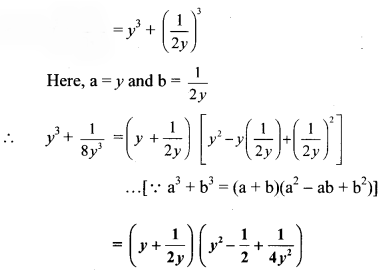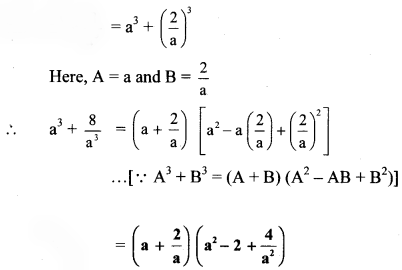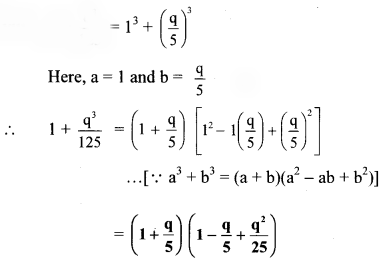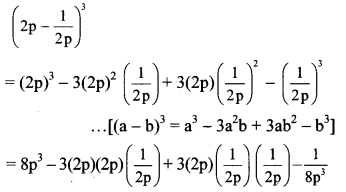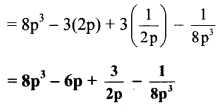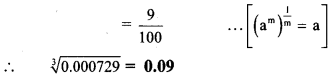Prasanna

Balbharti Maharashtra State Board Class 8 Maths Solutions covers the Practice Set 6.3 8th Std Maths Answers Solutions Chapter 6 Factorisation of Algebraic Expressions.

Practice Set 6.3 8th Std Maths Answers Chapter 6 Factorisation of Algebraic Expressions

Question 1.
Factorize
i. y³ – 27
ii. x³ – 64y³
iii. 27m³ – 216n³
iv. 125y³ – 1
v. \(8 p^{3}-\frac{27}{p^{3}}\)
vi. 343a³ – 512b³
vii. 64x³ – 729y³
viii. \(16 a^{3}-\frac{128}{b^{3}}\)
Solution:
i. y³ – 27
= y³ – (3)³
Here, a = y and b = 3
∴ y³ – 27 = (y – 3)[y² + y(3) + (3)2]
…[∵ a³ – b³ = (a – b) (a² + ab + b²)]
= (y – 3)(y² + 3y + 9)

ii. x³ – 64y³
= x³ – (4y)³
Here, a = x and b = 4y
∴ x³ – 64y³ = (x – 4y)[x² + x(4y) + (4y)²]
…[∵ a³ – b³ = (a – b)(a² + ab + b²)]
= (x – 4y)(x² + 4xy + 16y²)

iii. 27m³ – 216n³
= 27 (m³ – 8n³)
… [Taking out the common factor 27]
= 27 [m³ – (2n)³]
Here, a = m and b = 2n
∴ 27m³ – 216n³
= 27 {(m – 2n) [m² + m(2n) + (2n)²]}
….[∵ a³ – b³ = (a – b) (a² + ab + b²)]
= 27 (m – 2n)(m² + 2mn + 4n²)

iv. 125y³ – 1
= (5y)³ – 1³
Here, a = 5y and b = 1
∴ 125y³ – 1 = (5y – 1) [(5y)² + (5y)(1) + (1)²]
…[∵ a³ – b³ = (a – b)(a² + ab + b²)]
= (5y – 1) (25y² + 5y + 1)

v. \(8 p^{3}-\frac{27}{p^{3}}\)

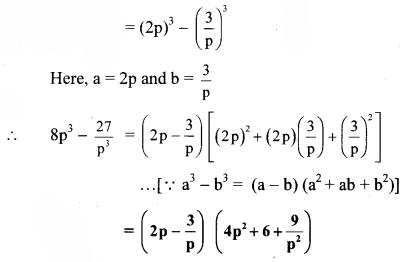
vi. 343a³ – 512b³
= (7a)³ – (8b)³
Here, A = 7a and B = 8b
∴ 343a³ – 512b³
= (7a – 8b) [(7a)² + (7a)(8b) + (8b)²]
…[∵ A³ – B³ = (A – B)(A² + AB + B²)]
= (7a – 8b) (49a² + 56ab + 64b²)

vii. 64x³ – 729y³
= (4x)³ – (9y)³
Here, a = 4x and b = 9y
∴ 64x³ – 729y³
= (4x – 9y) [(4x)² + (4x) (9y) + (9y)²]
…[∵ a³ – b³ = (a – b)(a² + ab + b²)]
= (4x – 9y) (16x² + 36xy + 81y²)

viii. \(16 a^{3}-\frac{128}{b^{3}}\)

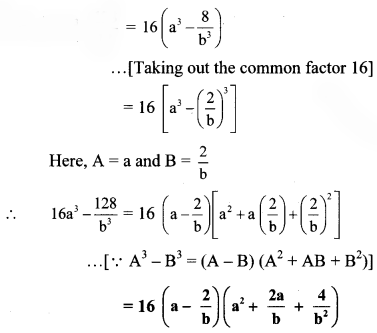
Question 2.
Simplify:
i. (x + y)³ – (x – y)³
ii. (3a + 5b)³ – (3a – 5b)³
iii. (a + b)³ – a³ – b³
iv. p³ – (p + 1)³
v. (3xy – 2ab)³ – (3xy + 2ab)³
Solution:
i. (x + y)³ – (x – y)³
Here, a = x + y and b = x – y
(x + y)³ – (x – y)³
= [(x + y) – (x – y)] [(x + y)² + (x + y) (x – y) + (x – y)]
…[a³ – b³ = (a – b)(a² + ab + b²)]
= (x + y – x + y) [(x² + 2xy + y²) + (x² – y²) + (x² – 2xy + y²)]
= 2y(x² + x² + x² + 2xy – 2xy + y² – y² + y²)
= 2y (3x² + y²)
= 6x²y + 2y³

ii. (3a + 5b)³ – (3a – 5b)³
Here, A = 3a + 5b and B = 3a – 5b
= [(3a + 5b) – (3a – 5b)] [(3a + 5b)² + (3a + 5b) (3a – 5b) + (3a – 5b)²]
…[∵ A³ – B³ = (A – B)(A² + AB + B²)]
= (3a + 5b – 3a + 5b) [(9a² + 30ab + 25b²) + (9a² – 25b²) + (9a² – 30ab + 25b²)]
= 10b (9a² + 9a² + 9a² + 30ab – 30ab + 25b² – 25b² + 25b²)
= 10b (27a² + 25b²)
= 270a²b + 250b³

iii. (a + b)³ – a³ – b³
= a³ + 3a²b + 3ab² + b³ – a³ – b³
= 3a²b + 3ab²

iv. p³ – (p + 1)³
= p³ – (p³ + 3p² + 3p + 1) …[∵ (a + b)³ = a³ + 3a²b + 3ab² + b³]
= p³ – p³ – 3p² – 3p – 1
= – 3p² – 3p – 1

v. (3xy – 2ab)³ – (3xy + 2ab)³
Here, A = 3xy – 2ab and B = 3xy + 2ab
∴ (3xy – 2ab)³ – (3xy + 2ab)³
= [(3xy – 2ab) – (3xy + 2ab)] [(3xy – 2ab)² + (3xy – 2ab) (3xy + 2ab) + (3xy + 2ab)²]
…[∵ A³ – B³ = (A – B) (A² + AB + B²)]
= (3xy – 2ab – 3xy – 2ab) [(9x²y² – 12xyab + 4a²b²) + (9x²y² – 4a²b²) + (9x²y² + 12xyab + 4a²b²)]
= (- 4ab) (9x²y² + 9x²y² + 9x²y² – 12xyab + 12xyab + 4a²b² – 4a²b² + 4a²b²)
= (- 4ab) (27 xy² + 4a²b²)
= -108x²y²ab – 16a³b³

Balbharti Maharashtra State Board Class 8 Maths Solutions covers the Practice Set 6.2 8th Std Maths Answers Solutions Chapter 6 Factorisation of Algebraic Expressions.

Practice Set 6.2 8th Std Maths Answers Chapter 6 Factorisation of Algebraic Expressions

Question 1.
Factorise:
i. x³ + 64y³
ii. 125p³ + q³
iii. 125k³ + 27m³
iv. 2l³ + 432m³
v. 24a³ + 81b³
vi. \(y^{3}+\frac{1}{8 y^{3}}\)
vii. \(\mathrm{a}^{3}+\frac{8}{\mathrm{a}^{3}}\)
viii. \(1+\frac{\mathrm{q}^{3}}{125}\)
Solution:
i. x³ + 64y³
= x³ + (4y)³
Here, a = x and b = 4y
∴ x³ + 64y³ = (x + 4y) [x² – x(4y) + (4y)²]
….[∵ a³ + b³ = (a + b)(a² – ab + b²)]
= (x + 4y)(x² – 4xy + 16y²)

ii. 125p³ + q³
= (5p)³ + q³
Here, a = 5p and b = q
∴ 125p³ + q³ = (5p + q)[(5p)² – (5p)(q) + q²]
…[∵ a³ + b³ = (a + b)(a² – ab + b²)]
= (5p + q)(25p² – 5pq + q²)

iii. 125k³ + 27m³
= (5k)³ + (3m)³
Here, a = 5k and b = 3m
∴ 125k³ + 27m³
= (5k + 3m) [(5k)² – (5k)(3m) + (3m)²]
…[∵ a³ + b³ = (a + b)(a² – ab + b²)]
= (5k + 3m)(25k² – 15km + 9m²)

iv. 2l³ + 432m³
= 2 (l³ + 216m³)
… [Taking out the common factor 2]
= 2[l³ + (6m)³]
Here, a = l and b = 6m
2l³ + 432m³ = 2 {(l + 6m)[l² – l(6m) + (6m)²]}
…[∵ a³ + b³ = (a + b)(a² – ab + b²)]
= 2(l + 6m)(l² – 6lm + 36m²)

v. 24a³ + 81b³
…[Taking out the common factor 3]
= 3 [(2a)³ + (3b)³]
Here, A = 2a and B = 3b
∴ 24a³ + 81b³
= 3 {(2a + 3b) [(2a)² – (2a)(3b) + (3b)²]}
…[∵ A³ + B³ = (A + B) (A² – AB + B²)]
= 3(2a + 3b)(4a² – 6ab + 9b²)

vi. \(y^{3}+\frac{1}{8 y^{3}}\)

vii. \(\mathrm{a}^{3}+\frac{8}{\mathrm{a}^{3}}\)

viii. \(1+\frac{\mathrm{q}^{3}}{125}\)

Balbharti Maharashtra State Board Class 8 Maths Solutions covers the Practice Set 6.1 8th Std Maths Answers Solutions Chapter 6 Factorisation of Algebraic Expressions.

Practice Set 6.1 8th Std Maths Answers Chapter 6 Factorisation of Algebraic Expressions

Question 1.
Factorize:
i. x² + 9x + 18
ii. x² – 10x + 9
iii. y² + 24y + 144
iv. 5y² + 5y – 10
v. p² – 2p – 35
vi. p² – 7p – 44
vii. m² – 23m + 120
viii. m² – 25m + 100
ix. 3x² + 14x + 15
x. 2x² + x – 45
xi. 20x² – 26x + 8
xii. 44x² – x – 3
Solution:
i. x² + 9x + 18
= x² + 6x + 3x + 18
= x (x + 6) + 3(x + 6)
= (x + 6) (x + 3)

ii. x² – 10x + 9
= x² – 9x – x + 9
= x (x – 9) – 1(x – 9)
= (x – 9)(x – 1)

iii. y² + 24y + 144
= y² + 12y + 12y + 144
= y(y + 12) + 12(y + 12)
= (y + 12)(y + 12)

iv. 5y² + 5y – 10
= 5(y² + y – 2)
… [Taking out the common factor 5]
= 5(y² + 2y – y – 2)
= 5[y(y + 2) – 1(y + 2)]
= 5 (p + 2)(y- 1)

v. p² – 2p – 35
= p² – 7p + 5p – 35
= p(p – 7) + 5(p – 7)
= (p – 7)(p + 5)

vi. p² – 7p – 44
= p² – 11p + 4p – 44
= p(p – 11) + 4(p – 11)
= (p – 11)(p + 4)

vii. m² – 23m + 120
= m² – 15m – 8m + 120
= m (m – 15) – 8 (m – 15)
= (m – 15) (m – 8)

viii. m² – 25m + 100
= m² – 20m – 5m + 100
= m(m – 20) – 5(m – 20)
= (m – 20) (m – 5)

ix. 3x² + 14x + 15 3 × 15 = 45
= 3x² + 9x + 5x + 15
= 3x(x + 3) + 5(x + 3)
= (x + 3) (3x + 5)

x. 2x² + x – 45 2 × (- 45) = -90
= 2x² + 10x – 9x – 45
= 2x(x + 5) – 9 (x + 5)
= (x + 5) (2x – 9)

xi. 20x² – 26x + 8
= 2(10x² – 13x + 4) 10 × 4 = 40
… [Taking out the common factor 2]
= 2(10x² – 8x – 5x + 4)
= 2[2x(5x – 4) – 1(5x – 4)]
= 2 (5x – 4) (2x – 1)

xii. 44x² – x – 3 44 × (-3) = -132
= 44x² – 12x + 11x – 3
= 4x(11x – 3) + 1(11x – 3)
= (11x – 3) (4x + 1)

Balbharti Maharashtra State Board Class 8 Maths Solutions covers the Practice Set 5.3 8th Std Maths Answers Solutions Chapter 5 Expansion Formulae.

Practice Set 5.3 8th Std Maths Answers Chapter 5 Expansion Formulae

Question 1.
Expand:
i. (2m – 5)³
ii. (4 – p)³
iii. (7x – 9y)³
iv. (58)³
v. (198)³
vi. \(\left(2 p-\frac{1}{2 p}\right)^{3}\)
vii. \(\left(1-\frac{1}{a}\right)^{3}\)
viii. \(\left(\frac{x}{3}-\frac{3}{x}\right)^{3}\)
Solution:
i. Here, a = 2m and b = 5
(2m – 5)³
= (2m)³ – 3(2m)² (5) + 3(2m) (5)² – (5)³
… [(a – b)³ = a³ – 3a²b + 3ab² – b³]
= 8m³ – 3(4m²)(5) + 3(2m)(25) – 125
= 8m³ – 60m² + 150m – 125

ii. Here, a = 4 and b = p
(4 – p)³ = (4)³ – 3(4)²(p) + 3(4)(p)² – (p)³
… [(a – b)³ = a³ – 3a²b + 3ab² – b³]
= 64 – 3(16)(p) + 3(4)(p²) – p³
= 64 – 48p + 12p² – p³

iii. Here, a = 7x and b = 9y
(7x – 9y)³
= (7x)³ – 3(7x)² (9y) + 3 (7x)(9y)² – (9y)³
…[(a – b)³ = a³ – 3a²b + 3ab² – b³]
= 343x³ – 3(49x²)(9y) + 3(7x)(81y²) – 729y³
= 343x³ – 1323x²y + 1701xy² – 729y³

iv. (58)³ = (60 – 2)³
Here, a = 60 and b = 2
(58)³ = (60)³ – 3(60)²(2) + 3(60)(2)² – (2)³
… [(a – b)³ = a³ – 3a²b + 3ab² – b³]
= 216000 – 3(3600)(2) + 3(60)(4) – 8
= 216000 – 21600 + 720 – 8
=195112

v. (198)³ = (200 – 2)³
Here, a = 200 and b = 2
(198)³ = (200)³ – 3(200)²(2) + 3(200)(2)² – (2)³
… [(a – b)³ = a³ – 3a²b + 3ab² – b³]
= 8000000 – 3(40000)(2) + 3(200)(4) – 8
= 8000000 – 240000 + 2400 – 8
= 7762392

vi. Here, a = 2p and b = \(\frac { 1 }{ 2p }\)

vii. Here, A = 1 and B = \(\frac { 1 }{ a }\)

viii. Here, a = \(\frac { x }{ 3 }\) and b = \(\frac { 3 }{ x }\)

Question 2.
Simplify:
i. (2a + b)³ – (2a – b)³
ii. (3r – 2k)³ + (3r + 2k)³
iii. (4a – 3)³ – (4a + 3)³
iv. (5x – 7y)³ + (5x + 7y)³
Solution:
i. (2a + b)³ – (2a – b)³
= [(2a)³ + 3(2a)²(b) + 3 (2a)(b)² + (b)³] – [(2a)³ – 3(2a)²(b) + 3 (2a)(b)² – (b)³]
… [(a + b)³ = a³ + 3a²b + 3ab² + b³, (a – b)³ = a³ – 3a²b + 3ab² – b³]
= (8a³ + 12a²b + 6ab² + b³) – (8a³ – 12a²b + 6ab² – b³)
= 8a³ + 12a²b + 6ab² + b³ – 8a³ + 12a²b – 6ab² + b³
= 8a³ – 8a³ + 12a²b + 12a²b + 6ab² – 6ab² + b³ + b³
= 24a²b + 2b³

ii. (3r – 2k)³ + (3r + 2k)³
= [(3r)³ – 3(3r)²(2k) + 3(3r)(2k)² – (2k)³] + [(3r)³ + 3(3r)²(2k) + 3(3r)(2k)² + (2k)³]
… [(a – b)³ = a³ – 3a²b + 3ab² – b³, (a + b)³ = a³ + 3a²b + 3ab² + b³]
= (27r³ – 54r²k + 36rk² – 8k³) + (27r³ + 54r²k + 36rk² + 8k³)
= 27r³ – 54r²k + 36rk² – 8k³ + 27r³ + 54r²k + 36rk² + 8k³
= 27r³ + 27r³ – 54r²k + 54r²k + 36rk² + 36rk² – 8k³ + 8k³
= 54r³ + 72rk²

iii. (4a – 3)³ – (4a + 3)³
= [(4a)³ – 3(4a)² (3) + 3(4a)(3)² – (3)³] – [(4a)³ + 3(4a)²(3) + 3(4a)(3)² + (3)³]
… [(a – b)³ = a³ – 3a²b + 3ab² – b³, (a + b)³ = a³ + 3a²b + 3ab² + b³]
= (64a³ – 144a² + 108a – 27) – (64a³ + 144a² + 108a + 27)
= 64a³ – 144a² + 108a – 27 – 64a³ -144a² – 108a – 27
= 64a³ – 64a³ – 144a² – 144a² + 108a – 108a – 27 – 27
= -288a² – 54

iv. (5x – 7y)³ + (5x + 7y)³
= [(5x)³ – 3(5x)²(7y) + 3(5x)(7y)² – (7y)³] + [(5x)³ + 3(5x)² (7y) + 3(5x) (7y)² +(7y)³]
… [(a – b)³ = a³ – 3a²b + 3ab² – b³, (a + b)³ = a³ + 3a²b + 3ab² + b³]
= (125x³ – 525x²y + 735xy² – 343y³) + (125x³ + 525x²y + 735xy² + 343y³)
= 125x³ – 525x²y + 735xy² – 343y³ + 125x³ + 525x²y + 735xy² + 343y³
= 125x³ + 125x³ – 525x²y + 525x²y + 735xy² + 735xy² – 343y³ + 343y³
= 250x³ + 1470xy²

Maharashtra Board Class 8 Maths Chapter 5 Expansion Formulae Practice Set 5.3 Intext Questions and Activities

Question 1.
Make two cubes of side a and of side b each. Make six parallelopipeds; three of them measuring a × a × b and the remaining three measuring b × b × a. Arrange all these solid figures properly and make a cube of side (a + b). (Textbook pg. no. 25)
Solution:
(a + b)³ = a³ + 3a²b + 3ab² + b³
= a × a × a + 3 × a × a × b + 3 × a × b × b + b × b × b

Balbharti Maharashtra State Board Class 8 Maths Solutions covers the Practice Set 5.1 8th Std Maths Answers Solutions Chapter 5 Expansion Formulae.

Practice Set 5.1 8th Std Maths Answers Chapter 5 Expansion Formulae

Question 1.
Expand :
i. (a + 2)(a – 1)
ii. (m – 4)(m + 6)
iii. (p + 8) (p – 3)
iv. (13 + x)(13 – x)
v. (3x + 4y) (3x + 5y)
vi. (9x – 5t) (9x + 3t)
vii. \(\left(m+\frac{2}{3}\right)\left(m-\frac{7}{3}\right)\)
viii. \(\left(x+\frac{1}{x}\right)\left(x-\frac{1}{x}\right)\)
ix. \(\left(\frac{1}{y}+4\right)\left(\frac{1}{y}-9\right)\)
Solution:
i. (a + 2)(a – 1)
= a² + (2 – 1) a + 2 × (-1)
..[∵ (x + A) (x + B) = x² + (A + B)x + AB]
= a² + a – 2

ii. (m – 4)(m + 6)
= m² + (- 4 + 6) m + (-4) × 6
…[∵ (x + a) (x + b) = x² + (a + b)x + ab]
= m² + 2m – 24

iii. (p + 8) (p – 3)
= p² + (8 – 3) p + 8 x (-3)
…[∵ (x + a) (x + b) = x² + (a + b)x + ab]
= p² + 5p – 24

iv. (13 + x) (13 – x)
= (13)² + (x – x) 13 + x × (-x)
…[∵ (x + a) (x + b) = x² + (a + b)x + ab]
= 169 + 0 × 13 – x²
= 169 – x²

v. (3x + 4y) (3x + 5y)
= (3x)² + (4y + 5y) 3x + 4y × 5y
…[∵ (x + a) (x + b) = x² + (a + b)x + ab]
= 9x² + 9y × 3x + 20y²
= 9x² + 27xy + 20y²

vi. (9x – 5t) (9x + 3t)
= (9x)² + [(-5t) + 3t] 9x + (-5t) × 3t
…[∵ (x + a) (x + b) = x² + (a + b)x + ab]
= 81x² + (-2t) × 9x – 15t²
= 81x² – 18xt – 15t²

vii. \(\left(m+\frac{2}{3}\right)\left(m-\frac{7}{3}\right)\)

viii. \(\left(x+\frac{1}{x}\right)\left(x-\frac{1}{x}\right)\)

ix. \(\left(\frac{1}{y}+4\right)\left(\frac{1}{y}-9\right)\)

Maharashtra Board Class 8 Maths Chapter 5 Expansion Formulae Practice Set 5.1 Intext Questions and Activities

Question 1.
Use the above formulae to fill proper terms in the following boxes. (Textbook pg. no. 23)

1. (x + 2y)² = x² + ___ + 4y²
2. (2x – 5y)² = __ – 20xy + __
3. (101)² = (100 + 1)² = ___+ ___ + 1² = ___
4. (98)² = (100 – 2)² = 10000 – ___ + ___ = ___
5. (5m + 3n) (5m – 3n) = ___ – ___ = ___ – ___

Solution:

1. (x + 2y)² = x² + 4xy + 4y²
2. (2x – 5y)² = 4x² – 20xy + 25y²
3. (101)² = (100 + 1)² = 10000 + 200 + 1² = 10201
4. (98)² = (100 – 2)² = 10000 – 400 + 4 = 9604
5. (5m + 3n) (5m – 3n) = (5m)² – (3n)² = 25m² – 9n²

Question 2.
Expand (x + a) (x + b) using formulae for areas of a square and a rectangle. (Textbook pg. no. 23)

(x + a) (x + b) = x² + ax + bx + ab
(x + a) (x + b) = x² + (a + b) x + ab
Solution:

∴ (x + a) (x + b) = x² + ax + bx + ab
∴ (x + a) (x + b) = x² + (a + b) x + ab

Balbharti Maharashtra State Board Class 8 Maths Solutions covers the Practice Set 5.2 8th Std Maths Answers Solutions Chapter 5 Expansion Formulae.

Practice Set 5.2 8th Std Maths Answers Chapter 5 Expansion Formulae

Question 1.
Expand:
i. (k + 4)³
ii. (7x + 8y)³
iii. (7x + m)³
iv. (52)³
v. (101)³
vi. \(\left(x+\frac{1}{x}\right)^{3}\)
vii. \(\left(2 m+\frac{1}{5}\right)^{3}\)
viii. \(\left(\frac{5 x}{y}+\frac{y}{5 x}\right)^{3}\)
Solution:
i. Here, a = k and b = 4
(k + 4)³ = (k)³ + 3(k)² (4) + 3(k)(4)² + (4)³
…[∵ (a + b)³ = a³ + 3a²b + 3ab² + b³]
= k³ + 12k² + 3(k)(16) + 64
= k³ + 12k² + 48k + 64

ii. Here, a = 7x and b = 8y
(7x + 8y)³
= (7x)³ + 3(7x)² (8y) + 3(7x) (8y)² + (8y)³
…[∵ (a + b)³ = a³ + 3a²b + 3ab² + b³]
= 343x³ + 3(49x²)(8y) + 3(7x)(64y²) + 512y³
= 343x³ + 1176x²y + 1344xy² + 512y³

iii. Here, a = 7 and b = m
(7 + m)³ = (7)³ + 3(7)²(m) + 3(7)(m)² + (m)³
…[∵ (a + b)³ = a³ + 3a²b + 3ab² + b³]
= 343 + 3(49)(m) + 3(7)(m²) + m³
= 343 + 147m + 21m² + m³

iv. (52)³ = (50 + 3)³
Here, a = 50 and b = 2
(52)³ = (50)³ + 3(50)² (2) + 3(50)(2)² + (2)³
…[∵ (a + b)³ = a³ + 3a²b + 3ab² + b³]
= 125000 + 3(2500)(2) + 3(50)(4) + 8
= 125000 + 15000 + 600 + 8
=140608

v. (101)³ = (100 + 1)³
Here, a = 100 and b = 1
(101)³
= (100)³ + 3(100)²(1) + 3(100)(1)² + (1)³
…[∵ (a + b)³ = a³ + 3a²b + 3ab² + b³]
= 1000000 + 3(10000) + 3(100) (1) + 1
= 1000000 + 30000 + 300 + 1
= 1030301

vi. Here, a = x and b = \(\frac { 1 }{ x }\)

vii. Here, a = 2m and b = \(\frac { 1 }{ 5 }\)

viii. Here, a = \(\frac { 5x }{ y }\) and b = \(\frac { y }{ 5x }\)

Balbharti Maharashtra State Board Class 8 Maths Solutions covers the Practice Set 4.1 8th Std Maths Answers Solutions Chapter 4 Altitudes and Medians of a Triangle.

Practice Set 4.1 8th Std Maths Answers Chapter 4 Altitudes and Medians of a Triangle

Question 1.
In ∆LMN, ___ is an altitude and __ is a median, (write the names of appropriate segments.)

Solution:
In ∆LMN, seg LX is an altitude and seg LY is a median.

Question 2.
Draw an acute angled ∆PQR. Draw all of its altitudes. Name the point of concurrence as ‘O’.
Solution:

Question 3.
Draw an obtuse angled ∆STV. Draw its medians and show the centroid.
Solution:

Question 4.
Draw an obtuse angled ∆LMN. Draw its altitudes and denote the ortho centre by ‘O’.
Solution:

Question 5.
Draw a right angled ∆XYZ. Draw its medians and show their point of concurrence by G.
Solution:

Question 6.
Draw an isosceles triangle. Draw all of its medians and altitudes. Write your observation about their points of concurrence.
Solution:

The point of concurrence of medians i.e. G and that of altitudes i.e. O lie on the same line PS which is the perpendicular bisector of seg QR.

Question 7.
Fill in the blanks.
Point G is the centroid of ∆ABC.
i. If l(RG) = 2.5, then l(GC) = ___
ii. If l(BG) = 6, then l(BQ) = ____
iii. If l(AP) = 6, then l(AG) = ___ and l(GP) = ___.

Solution:
The centroid of a triangle divides each median in the ratio 2:1.
i. Point G is the centroid and seg CR is the median.
∴ \(\frac{l(\mathrm{GC})}{l(\mathrm{RG})}=\frac{2}{1}\)
∴ \(\frac{l(\mathrm{GC})}{2.5}=\frac{2}{1}\) ……[∵ l(RG) = 2.5]
∴ l(GC) × 1 = 2 × 2.5
∴ l(GC) = 5

ii. Point G is the centroid and seg BQ is the median.
∴ \(\frac{l(\mathrm{BG})}{l(\mathrm{GQ})}=\frac{2}{1}\)
∴ \(\frac{6}{l(\mathrm{GQ})}=\frac{2}{1}\) …..[∵ l(BG) = 6]
∴ 6 × 1 = 2 × l(GQ)
∴ \(\frac { 6 }{ 2 }\) = l(GQ)
∴ 3 = l(GQ)
i.e. l(GQ) = 3
Now, l (BQ) = l(BG) + l(GQ)
∴ l(BQ) = 6 + 3
∴ l(BQ) = 9

iii. Point G is the centroid and seg AP is the median.
∴ \(\frac{l(\mathrm{AG})}{l(\mathrm{GP})}=\frac{2}{1}\)
∴ l(AG) = 2 l(GP) …..(i)
Now, l(AP) = l(AG) + l(GP) … (ii)
∴ l(AP) = 2l(GP) + l(GP) … [From (i)]
∴ l(AP) = 3l(GP)
∴ 6 = 3l(GP) ..[∵ l(AP) = 6]
∴ \(\frac { 6 }{ 3 }\) = l(GP)
∴ 2 = l(GP)
i.e. l(GP) = 2
l(AP) = l(AG) + l(GP) …[from (ii)]
∴ 6 = l(AG) + 2
∴ l(AG) = 6 – 2
∴ l(AG) = 4

Maharashtra Board Class 8 Maths Chapter 4 Altitudes and Medians of a Triangle Practice Set 4.1 Intext Questions and Activities

Question 1.
Draw a line. Take a point outside the line. Draw a perpendicular from the point to the line with the help of a set-square (Textbook pg. no, 19)
Solution:
Step 1: Draw a line l and a point P lying outside it.

Step 2: By placing a set-square on line l, draw a perpendicular to the line from point P.

Question 2.
Draw an acute angled ∆ABC and all its altitudes. Observe the location of the orthocentre. (Textbook pg. no. 20)
Solution:

Point O is the orthocentre.
Orthocentre lies in the interior of ∆ABC.

Question 3.
Draw a right angled triangle and draw all its altitudes. Write the point of concurrence. (Textbook: pg, no. 20)
Solution:

Point Q is the orthocentre.
The point of concurrence of altitudes PQ, QR and QS is Q.

Question 4.
i. Draw an obtuse angled triangle and all its altitudes.
ii. Do they intersect each other?
Draw the lines containing the altitudes. Observe that these lines are concurrent. (Textbook pg. no. 20)
Solution:
i.

Point O is the orthocentre.

ii. Yes, all the altitudes intersect at point O in the exterior of ∆PQR.

Question 5.
Draw three different triangles; a right angled triangle, an obtuse angled triangle and an acute angled triangle. Draw the medians of the triangles. Note that the centroid of each of them is in the interior of the triangle. (Textbook pg. no. 21)
Solution:
i. Right angled triangle:

ii. Obtuse angled triangle:

iii. Acute angled triangle:

Question 6.
Draw a sufficiently large ∆ABC.
Draw medians; seg AR, seg BQ and seg CP of ∆ABC.
Name the point of concurrence as G.
Measure the lengths of segments from the figure and fill in the boxes in the following table.

Observe that all of these ratios are nearly 2 : 1 (Textbook pg. no. 21)
Solution:

Question 7.
As shown in the given figure, a student drew ∆ABC using five parallel lines of a notebook. Then he found the centroid G of the triangle. How will you decide whether the location of G he found, is correct. (Textbook pg. no. 21)

Solution:
Draw seg AP ⊥ seg PE and seg EQ ⊥ seg QC.

Side AP || side EQ and AC is their transversal.
∴ ∠PAE ≅ ∠QEC …(i) [Corresponding angles]
In ∆ APE and ∆ EQC,
∠PAE ≅ ∠QEC …[From (i)]
∠APE ≅ ∠EQC
… [Each angle is of measure 90°]
side PE ≅ side QC
…. [Perpendicular distance between parallel lines]
∴ ∆ APE ≅ ∆ EQC … [By AAS test]
∴ AE = EC
… [Corresponding sides of congruent triangles]
∴ E is the midpoint of AC.
∴ seg BE is the median.
Similarly, seg CF is the median.
Since, the medians of a triangle are concurrent.
∴ G is the centroid of ∆ABC.

Question 8.
Draw an equilateral triangle. Find its circumcentre (C), incentre (I), centroid (G) and orthocentre (O). Write your observation. (Textbook pg. no. 22)
Solution:

From the figure, circumcentre (C), incentre (I), centroid (G) and orthocentre (O) of an equilateral triangle are the same.

Question 9.
Draw an isosceles triangle. Locate its centroid, orthocentre, circumcentre and incentre. Verify that they are collinear. (Textbook pg. no. 22)
Solution:

From the figure, centroid (G), orthocentre (O), circumcentre (C) and incentre (I) of an isosceles triangle lie on the same line AD.
∴ they are collinear.

Balbharti Maharashtra State Board Class 8 Maths Solutions covers the Practice Set 3.3 8th Std Maths Answers Solutions Chapter 3 Indices and Cube Root.

Practice Set 3.3 8th Std Maths Answers Chapter 3 Indices and Cube Root

Question 1.
Find the cube root of the following numbers.
i. 8000
ii. 729
iii. 343
iv. -512
v. -2744
vi. 32768
Solution:
i. 8000
= 2 × 2 × 2 × 10 × 10 × 10
= (2 × 10) × (2 × 10) × (2 × 10)
= (2 × 10)³
= 20³
∴ \(\sqrt[3]{8000}=20\)

ii. 729
= (3 × 3) × (3 × 3) × (3 × 3)
= (3 × 3)³
= 9³
∴ \(\sqrt[3]{729}=9\)

iii. 343
= 7 × 7 × 7
= 7³
∴ \(\sqrt[3]{343}=7\)

iv. -512
= 2 × 2 × 2 × 4 × 4 × 4
= (2 × 4) × (2 × 4) × (2 × 4)
= (2 × 4)³
= 8³
∴ – 512 = (- 8) × (- 8) × (- 8)
= (-8)³
∴ \(\sqrt[3]{-512}=-8\)

v. -2744
= 2 × 2 × 2 × 7 × 7 × 7
= (2 × 7) × (2 × 7) × (2 × 7)
= (2 × 7)³
= 14³
∴ -2744 = (-14) × (-14) × (-14)
= (-14)³
∴ \(\sqrt[3]{-2744}=-14\)

vi. 32768
= 2 × 2 × 2 × 4 × 4 × 4 × 4 × 4 × 4
= (2 × 4 × 4) × (2 × 4 × 4) × (2 × 4 × 4)
= (2 × 4 × 4)³
= 32³
∴ \(\sqrt[3]{32768}=32\)

Question 2.
Simplify:
i. \(\sqrt[3]{\frac{27}{125}}\)
ii. \(\sqrt[3]{\frac{16}{54}}\)
iii. If \(\sqrt[3]{729}=9\) then \(\sqrt[3]{0.000729}\) = ?
Solution:
i. \(\sqrt[3]{\frac{27}{125}}\)

ii. \(\sqrt[3]{\frac{16}{54}}\)

iii. \(\sqrt[3]{0.000729}\)


Note:
Here, number of decimal places in cube root = 6
∴ number of decimal places in cube of number = 2

Maharashtra Board Class 8 Maths Chapter 3 Indices and Cube Root Practice Set 3.3 Intext Questions and Activities

Question 1.
17 is a positive number. The cube of 17, which is 4913, is also a positive number. Cube of -6 is -216. Take some more positive and negative numbers and obtain their cubes. Find the relation between the sign of a number and the sign of its cube. (Textbook pg. no. 17)
Solution:
Consider, 6³ = 6 × 6 × 6 = 216 and (-4)³ = (- 4) × (- 4) × (- 4) = – 64
Thus, cube of a positive number is positive and cube of a negative number is negative.
∴ Sign of a number = sign of its cube.

Question 2.
In example 4 and 5 on textbook pg. no. 17, observe the number of decimal places in the number and number of decimal places in the cube of the number. Is there any relation between the two? (Textbook pg. no. 17)
Solution:
Yes, there is a relation between the number of decimal places in the number and its cube.
(1.2)³ = 1.728, (0.02)³ = 0.000008
No. of decimal places in 1.2 = 1
No. of decimal places in 1.728 = 3
No. of decimal places in 0.02 = 2
No. of decimal places in 0.000008 = 6
Thus, number of decimal places in cube of a number is three times the number of decimal places in that number.

Balbharti Maharashtra State Board Class 8 Maths Solutions covers the Practice Set 3.1 8th Std Maths Answers Solutions Chapter 3 Indices and Cube Root.

Practice Set 3.1 8th Std Maths Answers Chapter 3 Indices and Cube Root

Question 1.
Express the following numbers in index form.
i. Fifth root of 13
ii. Sixth root of 9
iii. Square root of 256
iv. Cube root of 17
v. Eighth root of 100
vi. Seventh root of 30
Solution:
i. \((13)^{\frac{1}{5}}\)
ii. \((9)^{\frac{1}{6}}\)
iii. \((256)^{\frac{1}{2}}\)
iv. \((17)^{\frac{1}{3}}\)
v. \((100)^{\frac{1}{8}}\)
vi. \((30)^{\frac{1}{7}}\)

Question 2.
Write in the form ‘nth root of a’ in each of the following numbers.
i. \((81)^{\frac{1}{4}}\)
ii. \((49)^{\frac{1}{2}}\)
iii. \((15)^{\frac{1}{5}}\)
iv. \((512)^{\frac{1}{9}}\)
v. \((100)^{\frac{1}{19}}\)
vi. \((6)^{\frac{1}{7}}\)
Solution:
i. Fourth root of 81.
ii. Square root of 49.
iii. Fifth root of 15.
iv. Ninth root of 512.
v. Nineteenth root of 100.
vi. Seventh root of 6.

Maharashtra Board Class 8 Maths Chapter 3 Indices and Cube Root Practice Set 3.1 Intext Questions and Activities

Question 1.
Using laws of indices, write proper numbers in the following boxes. (Textbook pg, no. 14)
i. \({ 3 }^{ 5 }\times { 3 }^{ 2 }={ 3 }^{ \left( \right) }\)
ii. \({ 3 }^{ 7 }\div { 3 }^{ 9 }={ 3 }^{ \left( \right) }\)
iii. \(({ 3 }^{ 4 })^{ 5 }={ 3 }^{ \left( \right) }\)
iv. \(5^{ -3 }=\frac { 1 }{ { 5 }^{ \left( \right) } }\)
v. \(5^{ 0 }=\left( \right) \)
vi. \(5^{ 1 }=\left( \right) \)
vii. \((5\times 7)^{ 2 }={ 5 }^{ \left( \right) }\times { 7 }^{ \left( \right) }\)
viii. \({ \left( \frac { 5 }{ 7 } \right) }^{ 3 }=\frac { { \left( \right) }^{ 3 } }{ { \left( \right) }^{ 3 } } \)
ix. \({ \left( \frac { 5 }{ 7 } \right) }^{ -3 }={ \left( \frac { \left( \right) }{ \left( \right) } \right) }^{ 3 }\)
Solution:
i. \({ 3 }^{ 5 }\times { 3 }^{ 2 }={ 3 }^{ 7 }\)
ii. \({ 3 }^{ 7 }\div { 3 }^{ 9 }={ 3 }^{ -2 }\)
iii. \(({ 3 }^{ 4 })^{ 5 }={ 3 }^{ 20 }\)
iv. \(5^{ -3 }=\frac { 1 }{ { 5 }^{ 3 } } \)
v. \(5^{ 0 }=1\)
vi. \(5^{ 1 }=5\)
vii. \((5\times 7)^{ 2 }={ 5 }^{ 2 }\times { 7 }^{ 2 }\)
viii. \({ \left( \frac { 5 }{ 7 } \right) }^{ 3 }=\frac { { 5 }^{ 3 } }{ { 7 }^{ 3 } } \)
ix. \({ \left( \frac { 5 }{ 7 } \right) }^{ -3 }={ \left( \frac { 7 }{ 5 } \right) }^{ 3 }\)

Balbharti Maharashtra State Board Class 8 Maths Solutions covers the Practice Set 3.2 8th Std Maths Answers Solutions Chapter 3 Indices and Cube Root.

Practice Set 3.2 8th Std Maths Answers Chapter 3 Indices and Cube Root

Question 1.
Complete the following table.

Solution:

Question 2.
Write the following numbers in the form of rational indices.
i. Square root of 5th power of 121.
ii. Cube of 4th root of 324.
iii. 5th root of square of 264.
iv. Cube of cube root of 3.
Solution:
i. \((121)^{\frac{5}{2}}\)
ii. \((324)^{\frac{3}{4}}\)
iii. \((264)^{\frac{2}{5}}\)
iv. \((3)^{\frac{3}{3}}\)