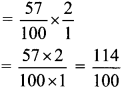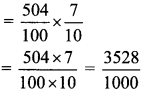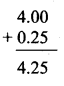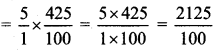Prasanna

Balbharti Maharashtra State Board Class 7 Maths Solutions covers the 7th Std Maths Practice Set 18 Answers Solutions Chapter 4 Angles and Pairs of Angles.

Angles and Pairs of Angles Class 7 Practice Set 18 Answers Solutions Chapter 4

Question 1.
Name the pairs of opposite rays in the figure alongside.

Solution:

1. Ray PL and ray PM
2. Ray PN and ray PT

Question 2.
Are the ray PM and PT opposite rays? Give reasons for your answer.

Solution:
No.
Ray PM and Ray PT do not form a straight line and hence are not opposite rays.

Maharashtra Board Class 7 Maths Chapter 4 Angles and Pairs of Angles Practice Set 18 Intext Questions and Activities

Question 1.
Observe the adjacent figure and answer the following questions. (Textbook pg. no. 28)

1. Name the rays in the figure alongside.
2. Name the origin of the rays
3. Name the angle in the given figure

Solution:

1. Ray BA and ray BC
2. Point B
3. ∠ABC or ∠CBA

Question 2.
Observe the adjacent figure and answer the following questions. (Textbook pg. no. 28)

1. Name the angle in the figure alongside.
2. Name the rays whose origin is point B

Solution:

1. ∠ABC or ∠CBA
2. Ray BA and ray BC

Balbharti Maharashtra State Board Class 6 Maths Solutions covers the Std 6 Maths Chapter 16 Quadrilaterals Class 6 Practice Set 38 Answers Solutions.

6th Standard Maths Practice Set 38 Answers Chapter 16 Quadrilaterals

Question 1.
Draw ₹XYZW and answer the following:
i. The pairs of opposite angles.
ii. The pairs of opposite sides.
iii. The pairs of adjacent sides.
iv. The pairs of adjacent angles.
v. The diagonals of the quadrilateral.
vi. The name of the quadrilateral in different ways.
Solution:

i. a. ∠XYZ and ∠XWZ
b. ∠YXW and ∠YZW

ii. a. side XY and side WZ
b. side XW and side YZ

iii. a. side XY and side XW
b. side WX and side WZ
c. side ZW and side ZY
d. side YZ and side YX

iv. a. ∠XYZ and ∠YZW
b. ∠YZW and ∠ZWX
c. ∠ZWX and ∠WXY
d. ∠WXY and ∠XYZ

v. Seg XZ and seg YW

vi. ₹XYZW
₹YZWX
₹ZWXY
₹WXYZ
₹XWZY
₹WZYX
₹ZYXW
₹YXWZ

Question 2.
In the table below, write the number of sides the polygon has.

Names	Quadrilateral	Octagon	Pentagon	Heptagon	Hexagon
Number of sides

Solution:

Names	Quadrilateral	Octagon	Pentagon	Heptagon	Hexagon
Number of sides	4	8	5	7	6

Question 3.
Look for examples of polygons in your surroundings. Draw them.
Solution:

Question 4.
We see polygons when we join the tips of the petals of various flowers. Draw these polygons and write down the number of sides of each polygon.
Solution:

Question 5.
Draw any polygon and divide it into triangular parts as shown here. Thus work out the sum of the measures of the angles of the polygon.

Solution:

Hexagon ABCDEF can be divided in 4 triangles namely ∆BAF, ∆BFE, ∆BED and ∆BCD
Sum of the measures of the angles of a triangle = 180°
∴ Sum of measures of the angles of the polygon ABCDEF = Sum of the measures of all the four triangles
= 180° + 180° + 180°+ 180°
= 720°
∴ The sum of the measures of the angles of the given polygon (hexagon) is 720°.

Maharashtra Board Class 6 Maths Chapter 16 Quadrilaterals Practice Set 38 Intext Questions and Activities

Question 1.
From your compass boxes, collect set squares of the same shapes and place them side by side in all possible different ways. What figures do you get? Write their names. (Textbook pg. no. 85)
a. Two set squares
b. Three set squares
c. four set squares
Solution:
a. Two set squares

b. Three set squares

c. four set squares

Question 2.
Kaprekar Number. (Textbook pg. no. 86)
i. Take any 4-digit number in which all the digits are not the same.
ii. Obtain a new 4-digit number by arranging the digits in descending order.
iii. Obtain another 4-digit number by arranging the digits of the new number in ascending order.
iv. Subtract the smaller of these two new numbers from the bigger number. The difference obtained will be a 4-digit number. If it is a 3-digit number, put a 0 in the thousands place. Repeat the above steps with the difference obtained as a result of the subtraction.
v. After some repetitions, you will get the number 6174. If you continue to repeat the same steps you will get the number 6174 every time. Let us begin with the number 8531.
8531 → 7173 → 6354 → 3087 → 8352 → 6174 → 6174
This discovery was made by the mathematician, Dattatreya Ramchandra Kaprekar. That is why the number 6174 was named the Kaprekar number.
Solution:

Balbharti Maharashtra State Board Class 7 Maths Solutions covers the 7th Std Maths Practice Set 17 Answers Solutions Chapter 4 Angles and Pairs of Angles.

Angles and Pairs of Angles Class 7 Practice Set 17 Answers Solutions Chapter 4

Question 1.
Write the measures of the supplements of the angles given below:
i. 15°
ii. 85°
iii. 120°
iv. 37°
v. 108°
vi. 0°
vii. a°
Solution:
i. Let the measure of the supplementary angle be x°.
∴ 15 + x = 180
∴ 15 + x – 15 = 180 – 15
….(Subtracting 15 from both sides)
∴ x = 165
∴ The measures of the supplement of an angle of 15° is 165°.

ii. Let the measure of the supplementary angle be x°.
∴ 85 + x = 180
∴ 85 + x – 85 = 180 – 85
….(Subtracting 85 from both sides)
∴ x = 95
∴ The measures of the supplement of an angle of 85° is 95°.

iii. Let the measure of the supplementary angle be x°.
∴ 120 + x = 180
∴ 120 + x – 120 = 180 – 120
….(Subtracting 120 from both sides)
∴ x = 60
∴ The measures of the supplement of an angle of 120° is 60°.

iv. Let the measure of the supplementary angle be x°.
∴ 37 + x = 180
∴ 37 + x – 37 = 180 – 37
….(Subtracting 37 from both sides)
∴ x = 143
∴ The measures of the supplement of an angle of 37° is 143°.

v. Let the measure of the supplementary angle be x°.
∴ 108 + x = 180
∴ 108 + x – 108 = 180 – 108
….(Subtracting 108 from both sides)
∴ x = 72
∴ The measures of the supplement of an angle of 108° is 72°.

vi. Let the measure of the supplementary angle be x°.
∴0 + x = 180
∴ x = 180
∴ The measures of the supplement of an angle of 0° is 180°.

vii. Let the measure of the supplementary angle be x°.
∴ a + x = 180
∴ a + x – a = 180 – a
….(Subtracting a from both sides) x = (180 – a)
∴ The measures of the supplement of an angle of a° is (180 – a)°.

Question 2.
The measures of some angles are given below. Use them to make pairs of complementary and supplementary angles.
m∠B = 60°
m∠N = 30°
m∠Y = 90°
m∠J = 150°
m∠D = 75°
m∠E = 0°
m∠F = 15°
m∠G = 120°
Solution:
i. m∠B + m∠N = 60° + 30°
= 90°
∴∠B and ∠N are a pair of complementary angles.

ii. m∠Y + m∠E = 90° + 0°
= 90°
∴∠Y and ∠E are a pair of complementary angles.

iii. m∠D + m∠F = 75° + 15°
= 90°
∴∠D and ∠F are a pair of complementary angles.

iv. m∠B + m∠G = 60° + 120°
= 180°
∴∠B and ∠G are a pair of supplementary angles.

v. m∠N + m∠J = 30° + 150°
= 180°
∴∠N and ∠J are a pair of supplementary angles.

Question 3.
In ΔXYZ, m∠Y = 90°. What kind of a pair do ∠X and ∠Z make?
Solution:
In ΔXYZ,
m∠X + m∠Y + m∠Z = 180° ….(Sum of the measure of the angles of a triangle is 180°)
∴m∠X + 90 + m∠Z = 180
∴m∠X + 90 + m∠Z – 90 = 180 – 90 ….(Subtracting 90 from both sides)
∴m∠X + m∠Z = 90°
∴∠X and ∠Z make a pair of complementary angles.

Question 4.
The difference between the measures of the two angles of a complementary pair is 40°. Find the measures of the two angles.
Solution:
Let the measure of one angle be x°.
∴Measure of other angle = (x + 40)°
x + (x + 40) = 90 …(Since, the two angles are complementary)
∴ 2x + 40 – 40 = 90 – 40 ….(Subtracting 40 from both sides)
∴2x = 50
∴x = \(\frac { 50 }{ 2 }\)
∴x = 25
∴x + 40 = 25 + 40
= 65
∴The measures of the two angles is 25° and 65°.

Question 5.
₹PTNM is a rectangle. Write the names of the pairs of supplementary angles.

Solution:
Since, each angle of the rectangle is 90°.
∴ Pairs of supplementary angles are:
i. ∠P and ∠M
ii. ∠P and ∠N
iii. ∠P and ∠T
iv. ∠M and ∠N
v. ∠M and ∠T
vi. ∠N and ∠T

Question 6.
If m∠A = 70°, what is the measure of the supplement of the complement of ∠A?
Solution:
Let the measure of the complement of ∠A be x° and the measure of its supplementary angle be y°.
m∠A + x = 90°
∴70 + x = 90
∴70 + x – 70 = 90 – 70 ….(Subtracting 70 from both sides)
∴x = 20
Since, x and y are supplementary angles.
∴x + y = 180
∴20 + y = 180
∴20 + y – 20 = 180 – 20 ….(Subtracting 20 from both sides)
∴y = 160
∴The measure of supplement of the complement of ∠A is 160°.

Question 7.
If ∠A and ∠B are supplementary angles and m∠B = (x + 20)°, then what would be m∠A?
Solution:
Since, ∠A and ∠B are supplementary angles.
∴m∠A + m∠B = 180
∴m∠A + x + 20 = 180
∴m∠A + x + 20 – 20 = 180 – 20 ….(Subtracting 20 from both sides)
∴m∠A + x = 160
∴m∠A + x – x = 160 – x ….(Subtracting x from both sides)
∴m∠A = (160 – x)°
∴The measure of ∠A is (160 – x)°.

Maharashtra Board Class 7 Maths Chapter 4 Angles and Pairs of Angles Practice Set 17 Intext Questions and Activities

Question 1.
Observe the figure and answer the following questions. (Textbook pg. no. 26)
T is a point on line AB.

1. What kind of angle is ∠ATB?
2. What is its measure?

Solution:

1. Straight angle
2. 180°

Balbharti Maharashtra State Board Class 6 Maths Solutions covers the Std 6 Maths Chapter 5 Decimal Fractions Class 6 Practice Set 16 Answers Solutions.

6th Standard Maths Practice Set 16 Answers Chapter 5 Decimal Fractions

Question 1.
If, 317 × 45 = 14265, then 3.17 × 4.5 = ?
Solution:
3.17 × 4.5
= 14.265

Question 2.
If, 503 × 217 = 109151, then 5.03 × 2.17 = ?
Solution:
5.03 x 2.17
= 10.9151

Question 3.
i. 2.7 × 1.4
ii. 6.17 × 3.9
iii. 0.57 × 2
iv. 5.04 × 0.7
Solution:
i. 2.7 × 1.4

= 3.75

ii. 6.17 × 3.9

= 24.063

iii. 0.57 × 2

= 1.14

iv. 5.04 × 0.7

= 3.528

Question 4.
Virendra bought 18 bags of rice, each bag weighing 5.250 kg. How much rice did he buy altogether? If the rice costs Rs 42 per kg, how much did he pay for it?
Solution:
Weight of one bag of rice = 5.250 kg
Number of bags of rice = 18
∴ Total Weight = 18 × 5.250

Cost of 1 kg of rice = Rs 42
∴ Cost of 94.5 kg of rice = 42 × 94.5

∴ Total rice bought by Virendra is 94.5 kg, and the amount paid for it is Rs 3969.

Question 5.
Vedika has 23.5 metres of cloth. She used it to make 5 curtains of equal size. If each curtain required 4 metres 25 cm to make, how much cloth is left over?
Solution:
We know, that 1 m = 100 cm
Cloth required to make 1 curtain = 4 m 25 cm
= 4 m + \(\frac { 25 }{ 100 }\) m
= 4 m + 0.25 m

= 4.25 m
∴ Cloth required to make 5 curtains = 5 × 4.25

= 21.25 m
Cloth remaining with Vedika = Total cloth with Vedika – Cloth used
= 23.5 m – 21.25 m

= 2.25 m
∴ The length of cloth remaining with Vedika is 2.25 m.

Balbharti Maharashtra State Board Class 7 Maths Solutions covers the 7th Std Maths Practice Set 16 Answers Solutions Chapter 4 Angles and Pairs of Angles.

Angles and Pairs of Angles Class 7 Practice Set 16 Answers Solutions Chapter 4

Question 1.
The measures of some angles are given below. Write the measures of their complementary angles.
i. 40°
ii. 63°
iii. 45°
iv. 55°
v. 20°
vi. 90°
vii. x°
Solution:
i. Let the measure of the complementary angle be x°.
∴ 40 + x = 90
∴ 40 + x – 40 = 90 – 40
….(Subtracting 40 from both sides)
∴ x = 50
∴ The measure of the complement of an angle of measure 40° is 50°.

ii. Let the measure of the complementary angle be x°.
∴ 63 + x = 90
∴ 63+x-63 = 90-63
….(Subtracting 63 from both sides)
∴ x = 27
∴ The measure of the complement of an angle of measure 63° is 27°.

iii. Let the measure of the complementary angle be x°.
∴ 45 + x = 90
∴ 45+x-45 = 90-45
….(Subtracting 45 from both sides)
∴ x = 45
∴ The measure of the complement of an angle of measure 45° is 45°.

iv. Let the measure of the complementary angle be x°.
∴ 55 + x = 90
∴ 55 + x-55 = 90-55
….(Subtracting 55 from both sides)
∴ x = 35
∴ The measure of the complement of an angle of measure 55° is 35°.

v. Let the measure of the complementary angle be x°.
∴ 20 + x = 90
∴ 20 + x – 20 = 90 – 20
….(Subtracting 20 from both sides)
∴ x = 70
∴ The measure of the complement of an angle of measure 20° is 70°.

vi. Let the measure of the complementary angle be x°.
∴ 90 + x = 90
∴ 90 + x – 90 = 90 – 90
….(Subtracting 90 from both sides)
∴ x = 0
∴ The measure of the complement of an angle of measure 90° is 0°.

vii. Let the measure of the complementary angle be a°.
∴ x + a = 90
∴ x + a – x = 90 – x
….(Subtracting x from both sides)
∴ a = (90 – x)
∴ The measure of the complement of an angle of measure x° is (90 – x)°.

Question 2.
(y – 20)° and (y + 30)° are the measures of complementary angles. Find the measure of each angle.
Solution:
(y – 20)° and (y + 30)° are the measures of complementary angles.
∴ (y – 20) + (y + 30) = 90
∴ y + y + 30 – 20 = 90
∴ 2y+10 = 90
∴ 2y = 90 – 10
∴ 2y = 80
∴ \(y=\frac { 80 }{ 2 }\)
= 40
Measure of first angle = (y – 20)° = (40 – 20)° = 20°
Measure of second angle = (y + 30)° = (40 + 30)° = 70°
∴ The measure of the two angles is 20° and 70°.

Maharashtra Board Class 7 Maths Chapter 4 Angles and Pairs of Angles Practice Set 16 Intext Questions and Activities

Question 1.
Observe the angles in the figure and enter the proper number in the empty place. (Textbook pg. no. 26)

1. m∠ABC = ___°.
2. m∠PQR = ___°.
3. m∠ABC + m∠PQR = ___°.

Solution:

1. 40
2. 50
3. 90

Note: Here, the sum of the measures of ∠ABC and ∠PQR is 90 °. Therefore, they are complementary angles.

Balbharti Maharashtra State Board Class 7 Maths Solutions covers the 7th Std Maths Practice Set 15 Answers Solutions Chapter 4 Angles and Pairs of Angles.

Angles and Pairs of Angles Class 7 Practice Set 15 Answers Solutions Chapter 4

Question 1.
Observe the figure and complete the table for ∠AWB.

Points in the interior
Points in the exterior
Points on the arms of the angles

Solution:

Points in the interior	point C, point R, point N, point X
Points in the exterior	point T, point U, point Q, point V, point Y
Points on the arms of the angles	point A, point W, point G, point B

Question 2.
Name the pairs of adjacent angles in the figures below.

Solution:
i. ∠ANB and ∠ANC
∠BNA and ∠BNC
∠ANC and ∠BNC

ii. ∠PQR and ∠PQT

Question 3.
Are the following pairs adjacent angles? If not, state the reason.

1. ∠PMQ and ∠RMQ
2. ∠RMQ and ∠SMR
3. ∠RMS and ∠RMT
4. ∠SMT and ∠RMS

Solution:

1. ∠PMQ and ∠RMQ are adjacent angles.
2. ∠RMQ and ∠SMR not adjacent angles since they do not have separate interiors.
3. ∠RMS and ∠RMT not adjacent angles since they do not have separate interiors.
4. ∠SMT and ∠RMS are adjacent angles.

Maharashtra Board Class 7 Maths Chapter 4 Angles and Pairs of Angles Practice Set 15 Intext Questions and Activities

Question 1.
Observe the figure alongside and write the answers. (Textbook pg. no. 24)

1. Write the name of the angle shown alongside___.
2. Write the name of its vertex___.
3. Write the names of its arms___.
4. Write the names of the points marked on its arms___.

Solution:

1. ∠ABC
2. Point B
3. Ray BA, ray BC
4. Points A, B, C

Balbharti Maharashtra State Board Class 7 Maths Solutions covers the 7th Std Maths Practice Set 14 Answers Solutions Chapter 3 HCF and LCM.

HCF and LCM Class 7 Practice Set 14 Answers Solutions Chapter 3

Question 1.
Choose the right option.
i. The HCF of 120 and 150 is __
(A) 30
(B) 45
(C) 20
(D) 120
Solution:
(A) 30

Hint:
120 = 2 x 2 x 2 x 3 x 5
150 = 2 x 3 x 5 x 5
∴ HCF of 120 and 150 = 2 x 3 x 5 = 30

ii. The HCF of this pair of numbers is not 1.
(A) 13,17
(B) 29,20
(C) 40, 20
(D) 14, 15
Solution:
(C) 40, 20

Hint:
40 = 2 x 2 x 2 x 5
20 = 2 x 2 x 5
∴ HCF of 40 and 20 = 2 x 5 = 10

Question 2.
Find the HCF and LCM.
i. 14,28
ii. 32,16
iii. 17,102,170
iv. 23,69
v. 21,49,84
Solution:
i. 14 = 2 x 7
28 = 2 x 14
= 2 x 2 x 7
∴ HCF of 14 and 28 = 2 x 7
= 14
LCM of 14 and 28 = 2 x 2 x 7
= 28

ii. 32 = 2 x 16
= 2 x 2 x 8
= 2 x 2 x 2 x 4
= 2 x 2 x 2 x 2 x 2
16 = 2 x 8
= 2 x 2 x 4
= 2 x 2 x 2 x 2
∴ HCF of 32 and 16 = 2 x 2 x 2 x 2
= 16
∴ LCM of 32 and 16 = 2 x 2 x 2 x 2 x 2
= 32

iii. 17 = 17 x 1
102 = 2 x 51
= 2 x 3 x 17
170 = 2 x 85
= 2 x 5 x 17
∴ HCF of 17, 102 and 170 = 17
∴ LCM of 17, 102 and 170 = 17 x 2 x 3 x 5
= 510

iv. 23 = 23 x 1
69 = 3 x 23
∴ HCF of 23 and 69 = 23
∴ LCM of 23 and 69 = 23 x 3
= 69

v. 21 = 3 x 7
49 = 7 x 7
84 = 2 x 42
= 2 x 2 x 21
= 2 x 2 x 3 x 7
∴ HCF of 21, 49 and 84 = 7
∴ LCM of 21, 49 and 84 = 7 x 3 x 7 x 2 x 2
= 588

Question 3.
Find the LCM.
i. 36, 42
ii. 15, 25, 30
iii. 18, 42, 48
iv. 4, 12, 20
v. 24, 40, 80, 120
Solution:
i. 36, 42

∴ LCM of 36 and 42 = 2 x 3 x 2 x 3 x 7
= 252

ii. 15, 25, 30

∴ LCM of 15, 25 and 30 = 5 x 3 x 5 x 2
= 150

iii. 18, 42, 48

∴ LCM of 18,42 and 48 = 2 x 3 x 2 x 2 x 3 x 7 x 2
= 1008

iv. 4, 12, 20

∴ LCM of 4, 12 and 20 = 2 x 2 x 3 x 5
= 60

v. 24, 40, 80, 120

∴ LCM of 24, 40, 80 and 120 = 2 x 2 x 2 x 5 x 3 x 2
= 240

Question 4.
Find the smallest number which when divided by 8,9,10,15,20 gives a remainder of 5 every time.
Solution:
Here, the smallest number for division is LCM of 8, 9, 10,15 and 20.
8 = 2 x 2 x 2
9 = 3 x 3
10 = 2 x 5
15 = 3 x 5
20 = 2 x 2 x 5
LCM of given numbers = 2 x 2 x 2 x 3 x 3 x 5 = 360
∴ Required, smallest number = LCM + Remainder
= 360 + 5
= 365
∴ The required smallest number is 365.

Question 5.
Reduce the fractions \(\frac{348}{319}, \frac{221}{247}, \frac{437}{551}\) to the lowest terms.
Solution:
i.

ii.

iii.

Question 6.
The LCM and HCF of two numbers are 432 and 72 respectively. If one of the numbers is 216, what is the other?
Solution:
Here, LCM = 432, HCF = 72, First number = 216
First number x Second number = LCM x HCF
∴ 216 x Second number = 432 x 72
∴ Second number = \(\frac{432 \times 72}{216}=432 \times \frac{72}{216}=432 \times \frac{1}{3}=144\)
∴ The other number is 144.

Question 7.
The product of two two-digit numbers is 765 and their HCF is 3. What is their LCM?
Solution:
Here, HCF = 3, Product of the given numbers = 765
Now, HCF x LCM = Product of the given numbers
∴ 3 x LCM = 765
∴ LCM = \(\frac { 765 }{ 3 }\) = 255
∴ The LCM of the two two-digit numbers is 255.

Question 8.
A trader has three bundles of string 392 m, 308 m and 490 m long. What is the greatest length of string that the bundles can be cut up into without any left over string?
Solution:
The required greatest length of the string is the highest common factor (HCF) of 392, 308 and 490.
∴ 392 = 2 x 2 x 2 x 7 x 7
308 = 2 x 2 x 7 x 11
490 = 2 x 7 x 7 x 5
∴ HCF of 392, 308 and 490 = 2 x 7
= 14
∴ The required greatest length of the string is 14 m.

Question 9.
Which two consecutive even numbers have an LCM of 180?
Solution:
LCM of two consecutive even numbers = 180
But, HCF of two consecutive even numbers = 2
Now, product of the given number = HCF x LCM
= 2 x 180
= 360
To find the two consecutive even numbers, we have to factorize 360.
360 = 2 x 2 x 2 x 3 x 3 x 5
360 = (2 x 3 x 3) x (2 x 2 x 5)
= 18 x 20
∴ The two consecutive even numbers whose LCM is 180 are 18 and 20.

Balbharti Maharashtra State Board Class 8 Maths Solutions covers the Practice Set 2.2 8th Std Maths Answers Solutions Chapter 2 Parallel Lines and Transversals.

Practice Set 2.2 8th Std Maths Answers Chapter 2 Parallel Lines and Transversals

Question 1.
Choose the correct alternative.
i. In the given figure, if line m || line n and line p is a transversal, then find x.

(A) 135°
(B) 90°
(C) 45°
(D) 40°
Solution:
(C) 45°

Hint:

line m || line n and line p is a transversal.
∴ m∠BFG + m∠FGD = 180°
…[Interior angles]
∴ 3x + x = 180°
∴ 4x = 180°
∴ x = \(\frac { 180 }{ 4 }\)
∴ x = 45°

ii. In the given figure, if line a || line b and line l is a transversal, then find x.

(A) 90°
(B) 60°
(C) 45°
(D) 30°
Solution:
(D) 30°

Hint:

line a || line b and line l is a transversal.
∴ m∠UVS = m∠PUV
…[Alternate angles]
= 4x
m∠UVS + m∠WVS = 180°
… [Angles in a linear pair]
∴ 4x + 2x = 180°
∴ 6x = 180°
∴ x = \(\frac { 180 }{ 6 }\)
∴ x = 30°

Question 2.
In the given figure, line p || line q. Line t and line s are transversals. Find measure of ∠x and ∠y using the measures of angles given in the figure.

Solution:

i. Consider ∠z as shown in figure.
line p || line q and line t is a transversal.
∴ m∠z = 40° …(i) [Corresponding angles]
m∠x + m∠z = 180° …[Angles in a linear pair]
∴ m∠x + 40o = 180° …[From(i)]
∴ m∠x= 180° – 40°
∴ m∠x = 140°

ii. Consider ∠w as shown in the figure.
m∠w + 70° = 180° …[Angles in a linear pair]
∴ m∠w = 180° – 70°
∴ m∠w = 110° …(ii)
line p || line q and line s is a transversal.
∴ m∠y = m∠w …[Alternate angles]
∴ m∠y =110° …[From (ii)]
∴ m∠x = 140°, m∠y = 110°

Question 3.
In the given figure, line p || line q, line l || line m. Find measures of ∠a, ∠b and ∠c, using the measures of given angles. Justify your answers.

Solution:
i. line p || line q and line l is a transversal.
∴ m∠a + 80° = 180° …[Interior angles]
∴ m∠a= 180° – 80°
∴ m∠a= 100°

ii. line l || line m and line p is a transversal.
∴ m∠c = 80° …(i) [Exterior alternate angles]

iii. line p || line q and line m is a transversal.
∴ m∠b = m∠c … [Corresponding angles]
m∠b = 80° …[From (i)]
∴ m∠a = 100°, m∠b = 80°, m∠c = 80°

Question 4.
In the given figure, line a || line b, line l is a transversal. Find the measures of ∠x, ∠y, ∠z using the given information.

Solution:
line a || line b and line l is a transversal.
∴ m∠x = 105° …(i) [Corresponding angles]

ii. m∠y = m∠x … [Vertically opposite angles]
∴ m∠y = 105° …[From (i)]

iii. m∠z + 105° = 180° …[Angles in a linear pair]
∴ m∠z = 180°- 105°
∴ m∠z = 75°
∴ m∠x = 105°, m∠y = 105°, m∠z = 75°

Question 5.
In the given figure, line p || line l || line q. Find ∠x with the help of the measures given in the figure.

Solution:

line p || line l and line IJ is a transversal.
m∠IJN = m∠JIH … [Alternate angles]
∴ m∠IJN = 40° …(i)
line l || line q and line MJ is a transversal.
m∠MJN = m∠JMK … [Alternate angles]
∴ m∠MJN = 30° …(ii)
Now, m∠x = m∠IJN + m∠MJN
…[Angle addition property]
= 40° + 30° …[From (i) and (ii)]
∴ m∠x = 70°

Maharashtra Board Class 8 Maths Chapter 2 Parallel Lines and Transversals Practice Set 2.2 Intext Questions and Activities

Question 1.
When two parallel lines are intersected by a transversal eight angles are formed. If the measure of one of these eight angles is given, can we find measures of remaining seven angles? (Textbook pg, no. 9)
Solution:
Yes, we can find the measures of the remaining angles.

In the given figure, line m || line n and line l is a transversal.
m∠a = 60°(say) …(i)
i. m∠a + m∠b = 180° …[Angles in a linear pair]
∴ 60° + m∠b =180° … [From (i)]
∴ m∠b = 180° – 60°
∴ m∠b = 120° …(ii)

ii. m∠c = m∠b …[Vertically opposite angles]
∴ m∠c = 120° .. .(iii) [From (ii)]

iii. m∠d = m∠a …[Vertically opposite angles]
∴ m∠d = 60° …(iv) [From (i)]

iv. m∠e = m∠d …[Alternate angles]
∴ m∠e = 60° … [From (iv)]

v. m∠f = m∠c …[Alternate angles]
∴ m∠f = 120° …[From (iii)]

vi. m∠g = m∠d …[Corresponding angles]
∴ m∠g = 60° … [From (iv)]

vii. m∠h = m∠c … [Corresponding angles]
∴ m∠h = 120° …[From (iii)]

Question 2.
As shown in the figure (A), draw two parallel lines and their transversal on a paper. Draw a copy of the figure on another blank sheet using a trace paper, as shown in the figure (B). Colour part Land part II with different colours. Cut out the two parts with a pair of scissors. Place, part I and part II on each angle in the figure A and answer the following questions. (Textbook pg. no. 9)

1. Which angles coincide with part I?
2. Which angles coincide with part II?

Solution:

1. ∠d, ∠f and ∠h coincide with part I.
2. ∠c, ∠e and ∠g coincide with part II.

Balbharti Maharashtra State Board Class 7 Maths Solutions covers the 7th Std Maths Practice Set 13 Answers Solutions Chapter 3 HCF and LCM.

HCF and LCM Class 7 Practice Set 13 Answers Solutions Chapter 3

Question 1.
Find the LCM:
i. 12, 15
ii. 6, 8, 10
iii. 18, 32
iv. 10, 15, 20
v. 45, 86
vi. 15, 30, 90
vii. 105, 195
viii. 12,15,45
ix. 63,81
x. 18, 36, 27
Solution:
i. 12, 15

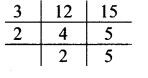
∴ LCM of 12 and 15 = 3 x 2 x 2 x 5
= 60

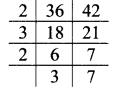
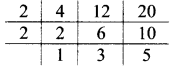
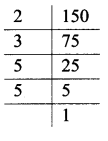
ii. 6, 8, 10

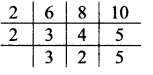
∴ LCM of 6, 8 and 10 = 2 x 2 x 3 x 2 x 5
= 120

iii. 18, 32

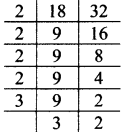
∴ LCM of 18 and 32 = 2 x 2 x 2 x 2 x 3 x 3 x 2
= 288

iv. 10, 15, 20

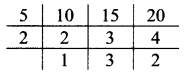
∴ LCM of 10, 15 and 20 = 5 x 2 x 3 x 2
= 60

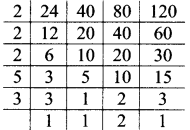
v. 45, 86

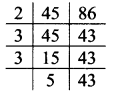
∴ LCM of 45 and 86 = 2 x 3 x 3 x 5 x 43
= 3870

vi. 15, 30, 90

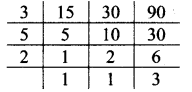
∴ LCM of 15,30 and 90 = 3 x 5 x 2 x 3
= 90

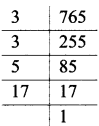
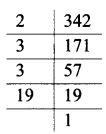
vii. 105, 195

∴ LCM of 105 and 195 = 5 x 3 x 7 x 13
= 1365

viii. 12, 15, 45

∴ LCM of 12, 15 and 45 = 3 x 3 x 2 x 5 x 2
= 180

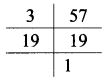
ix. 63, 81

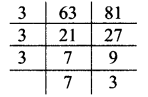
∴ LCM of 63 and 81 = 3 x 3 x 3 x 7 x 3
= 567

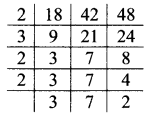
x. 18, 36, 27

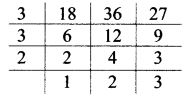
∴ LCM of 18, 36 and 27 = 3 x 3 x 2 x 2 x 3
= 108

Question 2.
Find the HCF and LCM of the numbers given below. Verify that their product is equal to the product of the given numbers:
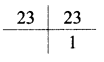
i. 32, 37
ii. 46, 51
iii. 15, 60
iv. 18, 63
v. 78, 104
Solution:
i. 32 = 2 x 16
= 2 x 2 x 8
= 2 x 2 x 2 x 4
= 2 x 2 x 2 x 2 x 2 x 1
37 = 37 x 1
∴ HCF of 32 and 37 =1
LCM of 32 and 37 = 2 x 2 x 2 x 2 x 2 x 37
= 1184
HCF x LCM = 1 x 1184
= 1184
Product of the given numbers = 32 x 37
= 1184
∴ HCF x LCM = Product of the given numbers.

ii. 46 = 2 x 23 x 1
51 = 3 x 17 x 1
∴ HCF of 46 and 51 = 1
LCM of 46 and 51 = 2 x 23 x 3 x 17
= 2346
HCF x LCM = 1 x 2346
= 2346
Product of the given numbers = 46 x 51
= 2346
∴ HCF x LCM = Product of the given numbers.

iii. 15 = 3 x 5
60 = 2 x 30
= 2 x 2 x 15
= 2 x 2 x 3 x 5
∴ HCF of 15 and 60 = 3 x 5
= 15
LCM of 15 and 60 = 3 x 5 x 2 x 2
= 60
HCF x LCM = 15 x 60
= 900
Product of the given numbers = 15 x 60
= 900
∴ HCF x LCM = Product of the given numbers.

iv. 18 = 2 x 9
= 2 x 3 x 3
63 = 3 x 21
= 3 x 3 x 7
∴ HCF of 18 and 63 = 3 x 3
= 9
LCM of 18 and 63 = 3 x 3 x 2 x 7
= 126
HCF x LCM = 9 x 126
= 1134
Product of the given numbers = 18 x 63
= 1134
∴ HCF x LCM = Product of the given numbers.

v. 78 = 2 x 39
= 2 x 3 x 13
104 = 2 x 52
= 2 x 2 x 26
= 2 x 2 x 2 x 13
∴ HCF of 78 and 104 = 2 x 13
= 26
LCM of 78 and 104 = 2 x 13 x 3 x 2 x 2
= 312
HCF x LCM = 26 x 312
= 8112
Product of the given numbers = 78 x 104
= 8112
∴ HCF x LCM = Product of the given numbers.

Maharashtra Board Class 7 Maths Chapter 3 HCF and LCM Practice Set 13 Intext Questions and Activities

Question 1.
Write the tables of the given numbers and find their LCM. (Textbook pg. no. 19)
i. 6, 7
ii. 8, 12
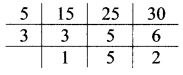
iii. 5, 6, 15
Solution:
i. Multiples of 6 : 6, 12, 18, 24, 30, 36, 42
Multiples of 7 : 7, 14, 21, 28, 35, 42, 49
∴ LCM of 6 and 7 = 42

ii. Multiples of 8 : 8, 16, 24, 32, 40
Multiples of 12 : 12, 24, 36, 48
∴ LCM of 8 and 12 = 24

iii. Multiples of 5 : 5, 10, 15, 20, 25, 30, 35
Multiples of 6 : 6, 12, 18, 24, 30, 36
Multiples of 15 : 15, 30, 45, 60
∴ LCM of 5,6 and 15 = 30

Balbharti Maharashtra State Board Class 7 Maths Solutions covers the 7th Std Maths Practice Set 11 Answers Solutions Chapter 3 HCF and LCM.

HCF and LCM Class 7 Practice Set 11 Answers Solutions Chapter 3

Question 1.
Factorize the following numbers into primes:
i. 32
ii. 57
iii. 23
iv. 150
v. 216
vi. 208
vii. 765
viii. 342
ix. 377
x. 559
Solution:
i. 32

∴ 32 = 2 × 2 × 2 × 2 × 2

ii. 57

∴ 57 = 3 × 19

iii. 23

∴ 23 = 23 × 1

iv. 150

∴ 150 = 2 × 3 × 5 × 5

v. 216

∴ 216 = 2 × 2 × 2 × 3 × 3 × 3

vi. 208

∴ 208 = 2 × 2 × 2 × 2 × 13

vii. 765

∴ 765 = 3 × 3 × 5 × 17

viii. 342

∴ 342 = 2 × 3 × 3 × 19

ix. 377

∴ 377 = 13 × 29

x. 559

∴ 559 = 13 × 43