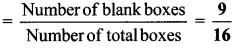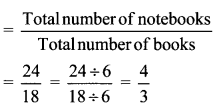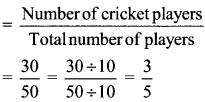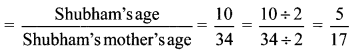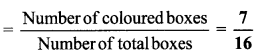Prasanna

Balbharti Maharashtra State Board Class 7 Maths Solutions covers the 7th Std Maths Practice Set 28 Answers Solutions Chapter 6 Indices.

Indices Class 7 Practice Set 28 Answers Solutions Chapter 6

Question 1.
Simplify:
i. a⁶ ÷ a⁴
ii. m⁵ ÷ m⁸
iii. p³ ÷ p¹³
iv. x¹⁰ ÷ x¹⁰
Solution:
i. a⁶ ÷ a⁴
= a^6-4
= a²

ii. m⁵ ÷ m⁸
= m^5-8
= m^-3

iii. p³ ÷ p¹³
= p^3-13
= p^-10

iv. x¹⁰ ÷ x¹⁰
= x^10-10
= x⁰
= 1

Question 2.
Find the value of:
i. (-7)¹² ÷ (-7)¹²
ii. 7⁵ ÷ 7³
iii. \(\left(\frac{4}{5}\right)^{3} \div\left(\frac{4}{5}\right)^{2}\)
iv. 4⁷ ÷ 4⁵
Solution:
i. (-7)¹² ÷ (-7)¹²
= (-7)^12-12
= (-7)⁰
= 1

ii. 7⁵ ÷ 7³
= 7^5-3
= 7²
= 49

iii. \(\left(\frac{4}{5}\right)^{3} \div\left(\frac{4}{5}\right)^{2}\)
\(=\left(\frac{4}{5}\right)^{3-2}=\frac{4}{5}\)

iv. 4 ÷ 4
= 4^7-5
= 4²
= 16

Balbharti Maharashtra State Board Class 6 Maths Solutions covers the Std 6 Maths Chapter 17 Geometrical Constructions Class 6 Practice Set 40 Answers Solutions.

6th Standard Maths Practice Set 40 Answers Chapter 17 Geometrical Constructions

Question 1.
Draw line l. Take point P anywhere outside the line. Using a set square draw a line PQ perpendicular to line l.
Solution:
Step 1:

Step 2:

line PQ ⊥ line l.

Question 2.
Draw line AB. Take point M anywhere outside the line. Using a compass and ruler, draw a line MN perpendicular to line AB.
Solution:
Step 1:

Step 2:

Step 3:

line MN ⊥ line AB.

Question 3.
Draw a line segment AB of length 5.5 cm. Bisect it using a compass and ruler.
Solution:
Step 1:

Step 2:

line MN is the perpendicular bisector of seg AB.

Question 4.
Take point R on line XY. Draw a perpendicular to XY at R, using a set square.
Solution:
Step 1:

Step 2:

line TR ⊥ line XY.

Maharashtra Board Class 6 Maths Chapter 17 Geometrical Constructions Practice Set 40 Questions and Activities

Question 1.
In the above construction, why must the distance in the compass be kept constant? (Textbook pg. no. 90)
Solution:
The point N is at equal distance from points P and Q.
If we change the distance of the compass while drawing arcs from points P and Q, we will not get a point which is at equal distance from P and Q. Hence, the distance in the compass must be kept constant.

Question 2.
The Perpendicular Bisector. (Textbook pg. no. 90)

1. A wooden ‘yoke’ is used for pulling a bullock cart. How is the position of the yoke determined?
2. To do that, a rope is used to measure equal distances from the spine/midline of the bullock cart. Which geometrical property is used here?
3. Find out from the craftsmen or from other experienced persons, why this is done.

Solution:

1. For the bullock cart to be pulled in the correct direction by the yoke, its Centre O should be equidistant from the either sides of the cart.
2. The property of perpendicular bisector is used to make the point equidistant from both the ends
3. A rope is used just like a compass to get equal distances from the spine/midline of bullock cart.

Question 3.
Take a rectangular sheet of paper. Fold the paper so that the lower edge of the paper falls on its top edge, and fold it over again from right to left. Observe the two folds that have formed on the . paper. Verify that each fold is a perpendicular bisector of the other. Then measure the following distances. (Textbook pg. no. 91)
i. l(XP)
ii. l(XA)
iii. l(XB)
iv. l(YP)
v. l(YA)

You will observe that l(XP) = l(YP), l(XA) = l(YA) and l(XB) = l(YB)
Therefore we can conclude that all points on the vertical fold (perpendicular bisector) are equidistant from the endpoints of the horizontal fold.
Solution:
[Note: Students should attempt this activity on their own.]

Balbharti Maharashtra State Board Class 6 Maths Solutions covers the Std 6 Maths Chapter 6 Bar Graphs Class 6 Practice Set 19 Answers Solutions.

6th Standard Maths Practice Set 19 Answers Chapter 6 Bar Graphs

Question 1.
The names of the heads of some families in a village and the quantity of drinking water their family consumes in one day are given below. Draw a bar graph for this data.
(Scale: On Y axis. 1 cm = 10 liters of water)

Name	Ramesh	Shobha	Ayub	Julie	Rahul
Liters of water Used	30 L	60 L	40 L	50L	55 L

Solution:

Question 2.
The names and numbers of animals in a certain zoo are given below. Use the data to make a bar graph. (Scale: On Y axis, 1 cm = 4 animals).

Animals	Deer	Tiger	Monkey	Rabbit	Peacock
Number	20	4	12	16	8

Solution:

Question 3.
The table below gives the number of children who took part in the various items of the talent show as part of the annual school gathering. Make a bar graph to show this data.
(Scale: On Y-axis, 1 cm = 4 children)

Programme	Theater	Dance	Vocal music	Instrumental music	One-act plays
Number of Children	24	40	16	8	4

Solution:

Question 4.
The number of customers who came to a juice centre during one week is given in the table below. Make two different bar graphs to show this data.
(On Y-axis, 1 cm = 10 customers, 1 cm = 5 customers)

Type of juice	Orange	Pineapple	Apple	Mango	Pomegranate
Number of customers	50	30	25	65	10

Solution:

Question 5.
Students planted trees in 5 villages of Sangli district. Make a bar graph of this data. (Scale: On Y-axis, 1 cm = 100 trees).

Name of Place	Dudhgaon	Bagni	Samdoli	Ashta	Kavathepiran
Number of Trees Planted	500	350	600	420	540

Solution:

Question 6.
Yashwant gives different amounts of time as shown below, to different exercises he does during the week. Draw a bar graph to show the details of his schedule using an appropriate scale.

Type of exercise	Running	Yogasanas	Cycling	Mountaineering	Badminton
Time	35 minutes	50 minutes	1 hr 10 min	\(1\frac { 1 }{ 2 }\) hours	45 minutes

Solution:
1 hour = 60 minutes
∴ 1 hour 10 minutes = 1 hour + 10 minutes = 60 minutes +10 minutes = 70 minutes
and \(1\frac { 1 }{ 2 }\) hours = 1 hour + \(\frac { 1 }{ 2 }\) hour = 60 minutes + 30 minutes = 90 minutes
The given table can be written as follows:

Type of Exercise	Running	Yogasanas	Cycling	Moutaineering	Badminton
Time	35 minutes	50 minutes	70 minutes	90 minutes	45 minutes

Question 7.
Write the names of four of your classmates. Beside each name, write his/her weight in kilograms. Enter this data in a table like the above and make a bar graph.
Solution:

Name of classmates	Weight (kg)
Rohan	32
Laxmi	28
Rakesh	40
Riya	36

Scale: On Y-axis, 1 cm = 4 kg [Note: Students can take their own examples]

Maharashtra Board Class 6 Maths Chapter 6 Bar Graphs Practice Set 19 Intext Questions and Activities

Question 1.
Collect bar graphs from newspapers or periodicals showing a variety of data. (Textbook pg. no. 38)
Solution:
(Student should attempt the activities on their own.)

Balbharti Maharashtra State Board Class 7 Maths Solutions covers the 7th Std Maths Practice Set 27 Answers Solutions Chapter 6 Indices.

Indices Class 7 Practice Set 27 Answers Solutions Chapter 6

Question 1.
Simplify:
i. 7⁴ × 7²
ii. (-11)⁵ × (-11)²
iii. \(\left(\frac{6}{7}\right)^{3} \times\left(\frac{6}{7}\right)^{5}\)
iv. \(\left(-\frac{3}{2}\right)^{5} \times\left(-\frac{3}{2}\right)^{3}\)
v. a¹⁶ × a⁷
vi. \(\left(\frac{\mathrm{P}}{5}\right)^{3} \times\left(\frac{\mathrm{P}}{5}\right)^{7}\)
Solution:
i. 7⁴ × 7²
= 7⁴⁺²
= 7⁶

ii. (-11)⁵ × (-11)²
= (-11)⁵⁺²
= (-11)⁷

iii. \(\left(\frac{6}{7}\right)^{3} \times\left(\frac{6}{7}\right)^{5}\)
\(=\left(\frac{6}{7}\right)^{3+5}=\left(\frac{6}{7}\right)^{8}\)

iv. \(\left(-\frac{3}{2}\right)^{5} \times\left(-\frac{3}{2}\right)^{3}\)
\(=\left(-\frac{3}{2}\right)^{5+3}=\left(-\frac{3}{2}\right)^{8}\)

v. a¹⁶ × a⁷
= a¹⁶⁺⁷
= a²³

vi. \(\left(\frac{\mathrm{P}}{5}\right)^{3} \times\left(\frac{\mathrm{P}}{5}\right)^{7}\)
\(=\left(\frac{\mathrm{P}}{5}\right)^{3+7}=\left(\frac{\mathrm{P}}{5}\right)^{10}\)

Balbharti Maharashtra State Board Class 6 Maths Solutions covers the Std 6 Maths Chapter 3 Integers Class 6 Practice Set 7 Answers Solutions.

6th Standard Maths Practice Set 7 Answers Chapter 3 Integers

Question 1.
Write the proper signs >, < or = in the boxes below:

1. -4 __ 5
2. 8 __ -10
3. +9 __ +9
4. -6 __ 0
5. 7 __ 4
6. 3 __ 0
7. -7 __ 7
8. -12 __ 5
9. -2 __ -8
10. -1 __ -2
11. 6 __ -3
12. -14 __ -14

Solution:

1. -4 < 5
2. 8 > -10
3. +9 = +9
4. -6 < 0
5. 7 > 4
6. 3 > 0
7. -7 < 7
8. -12 < 5
9. -2 > -8
10. -1 > -2
11. 6 > -3
12. -14 = -14

Balbharti Maharashtra State Board Class 6 Maths Solutions covers the Std 6 Maths Chapter 3 Integers Class 6 Practice Set 6 Answers Solutions.

6th Standard Maths Practice Set 6 Answers Chapter 3 Integers

Question 1.
Write the opposite number of each of the numbers given below.

Number	47	+52	-33	-84	-21	+16	-26	80
Opposite number

Solution:

Number	47	+52	-33	-84	-21	+16	-26	80
Opposite number	-47	-52	+33	+84	+21	-16	+26	-80

Balbharti Maharashtra State Board Class 6 Maths Solutions covers the Std 6 Maths Chapter 11 Ratio-Proportion Class 6 Practice Set 28 Answers Solutions.

6th Standard Maths Practice Set 28 Answers Chapter 11 Ratio-Proportion

6th Standard Maths Practice Set 28 Question 1.
In each example below, find the ratio of the first number to the second:
i. 24, 56
ii. 63,49
iii. 52, 65
iv. 84, 60
v. 35, 65
vi. 121, 99
Solution:
i. 24, 56
\(\frac{24}{56}=\frac{24 \div 8}{56 \div 8}=\frac{3}{7}\)
= 3:7

ii. 63,49
\(\frac{63}{49}=\frac{63 \div 7}{49 \div 7}=\frac{9}{7}\)
= 9:7

iii. 52, 65
\(\frac{52}{65}=\frac{52 \div 13}{65 \div 13}=\frac{4}{5}\)
= 4:5

iv. 84, 60
\(\frac{84}{60}=\frac{84 \div 12}{60 \div 12}=\frac{7}{5}\)
= 7:5

v. 35, 65
\(\frac{35}{65}=\frac{35 \div 5}{65 \div 5}=\frac{7}{13}\)
= 7:13

vi. 121, 99
\(\frac{121}{99}=\frac{121 \div 11}{99 \div 11}=\frac{11}{9}\)
= 11:9

6th Maths Practice Set 28 Question 2.
Find the ratio of the first quantity to the second.
i. 25 beads, 40 beads
ii. Rs 40, Rs 120
iii. 15 minutes, 1 hour
iv. 30 litres, 24 litres
v. 99 kg, 44000 grams
vi. 1 litre, 250 ml
vii. 60 paise, 1 rupee
viii. 750 grams, \(\frac { 1 }{ 2 }\) kg
ix. 125 cm, 1 metre
Solution:
i. Required Ratio = \(\frac{25}{40}=\frac{25 \div 5}{40 \div 5}=\frac{5}{8}\)

ii. Required Ratio = \(\frac{40}{120}=\frac{40 \div 40}{120 \div 40}=\frac{1}{3}\)

iii. 1 hour = 60 minutes
Required Ratio = \(\frac{15}{60}=\frac{15 \div 15}{60 \div 15}=\frac{1}{4}\)

iv. Required Ratio = \(\frac{30}{24}=\frac{30 \div 6}{24 \div 6}=\frac{5}{4}\)

v. 99 kg = 99 x 1000 grams = 99000 grams
Required Ratio = \(\frac{99000}{44000}=\frac{99000 \div 1000}{44000 \div 1000}=\frac{99}{44}\)
= \(\frac{99}{44}=\frac{99 \div 11}{44 \div 11}=\frac{9}{4}\)

vi. 1 litre, 250 ml
1 litre = 1000 ml
Required Ratio = \(\frac{1000}{250}=\frac{1000 \div 10}{250 \div 10}=\frac{100}{25}\)
= \(\frac{100}{25}=\frac{100 \div 25}{25 \div 25}=\frac{4}{1}\)

viii. 750 grams, \(\frac { 1 }{ 2 }\) kg
\(\frac { 1 }{ 2 }\) kg = \(\frac { 1000 }{ 2 }\) grams = 500 grams
Required Ratio = \(\frac{750}{500}=\frac{750 \div 10}{500 \div 10}=\frac{75}{50}\)
= \(\frac{75}{50}=\frac{75 \div 25}{50 \div 25}=\frac{3}{2}\)

ix. 125 cm, 1 metre
1 metre = 100 cm
Required Ratio = \(\frac{125}{100}=\frac{125 \div 25}{100 \div 25}=\frac{5}{4}\)

6th Std Maths Practice Set 28 Question 3.
Reema has 24 notebooks and 18 books. Find the ratio of notebooks to books.
Solution:
Ratio of notebooks to books

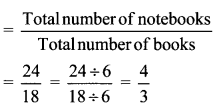
∴ The ratio of notebooks to books with Reema is \(\frac { 4 }{ 3 }\)

Practice Set 28 Question 4.
30 cricket players and 20 kho-kho players are training on a field. What is the ratio of cricket players to the total number of players?
Solution:
Total number of players = Cricket players + Kho-kho players
= 30 + 20 = 50
Ratio of cricket players to the total number of players

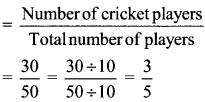
∴ The ratio of cricket players to the total number of players is \(\frac { 3 }{ 5 }\).

Question 5.
Snehal has a red ribbon that is 80 cm long and a blue ribbon 2.20 m long. What is the ratio of the length of the red ribbon to that of the blue ribbon?
Solution:
1 metre =100 cm
Length of the red ribbon = 80 cm
Length of the blue ribbon = 2.20 m = 2.20 x 100 cm
\(=\frac{220}{100} \times \frac{100}{1}=\frac{220 \times 100}{100 \times 1}\)
= 220 cm
∴ Ratio of length of the red ribbon to that of the blue ribbon

∴ The ratio of the length of the red ribbon to that of the blue ribbon is \(\frac { 4 }{ 11 }\).

11 Ratio Question 6.
Shubham’s age today is 12 years and his father’s is 42 years. Shubham’s mother is younger than his father by 6 years. Find the following ratios.
i. Ratio of Shubham’s age today to his mother’s age today.
ii. Ratio of Shubham’s mother’s age today to his father’s age today.
iii. The ratio of Shubham’s age to his mother’s age when Shubham was 10 years old.
Solution:
Shubham’s age today = 12 years
Shubham’s father’s age = 42 years
Shubham’s mother age = Shubham’s father’s age – 6 years
= 42 years – 6 years = 36 years

i. Ratio of Shubham’s age today to his mother’s age today

∴ The ratio of Shubham’s age today to his mother’s age today is \(\frac { 1 }{ 3 }\).

ii. Ratio of Shubham’s mother age today to his father’s age today

∴ The ratio of Shubham’s mother’s age today to his father’s age today is \(\frac { 6 }{ 7 }\).

iii. Shubham’s age today is 12 years and his mothers age is 36 years.
Hence when Shubham’s age was 10 years, his mother’s age was 34 years (i.e. 36 – 2 years).
Ratio of Shubham’s age to his mother’s age when Shubham was 10 years old

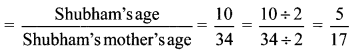
∴ The ratio of Shubham’s age to his mother’s age when Shubham was 10 years old is \(\frac { 5 }{ 17 }\)

Maharashtra Board Class 6 Maths Chapter 11 Ratio-Proportion Practice Set 28 Intext Questions and Activities

Question 1.
In the figure, colour some squares with any colour you like and leave some blank. (Textbook pg. no. 57)

i. Count all the boxes and write the number.
ii. Count the colored ones and write the number.
iii. Count the blank ones and write the number.
iv. Find the ratio of the colored boxes to the blank ones.
v. Find the ratio of the colored boxes to the total boxes.
vi. Find the ratio of the blank boxes to the total boxes.
Solution:
i. The number of all boxes is 16.
ii. The number of colored boxes is 7.
iii. The number of blank boxes is 9.
iv. Ratio of the colored boxes to the blank ones

v. Ratio of the colored boxes to the total boxes

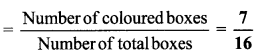
vi. Ratio of the blank boxes to the total boxes

Balbharti Maharashtra State Board Class 7 Maths Solutions covers the 7th Std Maths Practice Set 26 Answers Solutions Chapter 6 Indices.

Indices Class 7 Practice Set 26 Answers Solutions Chapter 6

Question 1.
Complete the table below:

Sr. No.	Indices (Numbers in index form)	Base	Index	Multiplication form	Value
i.	34	3	4	3 x 3 x 3 x 3	81
ii.	163
iii.		(-8)	2
iv.				\(\frac{3}{7} \times \frac{3}{7} \times \frac{3}{7} \times \frac{3}{7}\)	\(\frac { 81 }{ 2401 }\)
v.	(-13)4

Solution:

Sr. No.	Indices (Numbers in index form)	Base	Index	Multiplication form	Value
i.	34	3	4	3 x 3 x 3 x 3	81
ii.	163	16	3	16 x 16 x 16	4096
iii.	(-8)²	(-8)	2	-8 x -8	64
iv.	\(\left(\frac{3}{7}\right)^{4}\)	\(\frac { 7 }{ 7 }\)	4	\(\frac{3}{7} \times \frac{3}{7} \times \frac{3}{7} \times \frac{3}{7}\)	\(\frac { 81 }{ 2401 }\)
v.	(-13)4	-13	4	(-13) x (-13) x (-13) x (-13)	28561

Question 2.
Find the value of.
i. 2¹⁰
ii. 5³
iii. (-7)⁴
iv. (-6)³
v. 9³
vi. 8¹
vii. \(\left(\frac{4}{5}\right)^{3}\)
viii. \(\left(-\frac{1}{2}\right)^{4}\)
Solution:
i. 2¹⁰
= 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2
= 1024

ii. 5³
= 5 × 5 × 5
= 125

iii. (-7)⁴
= (-7) × (-7) × (-7) × (-7)
= 2401

iv. (-6)³
= (-6) × (-6) × (-6)
= -216

v. 9³
= 9 × 9 × 9
= 729

vi. 8¹
= 8

vii. \(\left(\frac{4}{5}\right)^{3}\)
\(=\frac{4}{5} \times \frac{4}{5} \times \frac{4}{5}=\frac{64}{125}\)

viii. \(\left(-\frac{1}{2}\right)^{4}\)
\(=\left(-\frac{1}{2}\right) \times\left(-\frac{1}{2}\right) \times\left(-\frac{1}{2}\right) \times\left(-\frac{1}{2}\right)=\frac{1}{16}\)

Balbharti Maharashtra State Board Class 7 Maths Solutions covers the 7th Std Maths Practice Set 25 Answers Solutions Chapter 5 Operations on Rational Numbers.

Operations on Rational Numbers Class 7 Practice Set 25 Answers Solutions Chapter 5

Question 1.
Simplify the following expressions.
i. 50 x 5 ÷ 2 + 24
ii. (13 x 4) ÷ 2 – 26
iii. 140 ÷ [(-11) x (-3) – (-42) ÷ 14 – 1)]
iv. {(220 – 140) + [10 x 9 + (-2 x 5) ]} – 100
v. \(\frac{3}{5}+\frac{3}{8} \div \frac{6}{4}\)
Solution:
i. 50 x 5 ÷ 2 + 24 = 250 ÷ 2 + 24
= 125 + 24
= 149

ii. (13 x 4) = 2 – 26
= 52 ÷ 2 – 26
= 26 – 26
= 0

iii. 140 ÷ [(-11) x (-3) – (-42) ÷ 14 – 1)]
= 140 ÷ [33 + 42 ÷ 14 – 1]
= 140 ÷ [33 + 3 – 1]
= 140 ÷ 35
= 4

iv. {(220 – 140) + [10 x 9 + (-2 x 5) ]} – 100
= {80 + [90 – 10]} – 100
= {80 + 80} – 100
= 160 – 100
= 60

v. \(\frac{3}{5}+\frac{3}{8} \div \frac{6}{4}\)
\(=\frac{3}{5}+\frac{3}{8} \times \frac{4}{6}\)
\(=\frac{3}{5}+\frac{1}{4}\)
\(=\frac{12}{20}+\frac{5}{20}=\frac{12+5}{20}=\frac{17}{20}\)

Maharashtra Board Class 7 Maths Chapter 5 Operations on Rational Numbers Practice Set 25 Intext Questions and Activities

Question 1.
Use the signs and numbers in the boxes and form an expression such that its value will be 112. (Textbook pg. no. 42)
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
[+ x ÷ -]
Solution:
{3 + (6 x 7) + (9 ÷ 3)} + {- 8 + 8 x 9}
Note: The above problem has many solutions. Students may write solution other than the one given.

Balbharti Maharashtra State Board Class 6 Maths Solutions covers the Std 6 Maths Chapter 3 Integers Class 6 Practice Set 5 Answers Solutions.

6th Standard Maths Practice Set 5 Answers Chapter 3 Integers

Question 1.
Add:

1. 8 + 6
2. 9 + (-3)
3. 5 + (-6)
4. – 7 + 2
5. – 8 + 0
6. – 5 + (-2)

Solution:

1. 8 + 6 = (+8) + (+6) = +14	2. 9 + (-3) = (+9) + (- 3) = +6	3. 5 + (-6) = (+5) + (-6) = -1
4. -7 + 2 = (-7) + (+2) = -5	5. -8 + 0 = (-8) + 0 = -8	6. -5 + (-2) = (-5) + (-2) = -7

Question 2.
Complete the table given below:

+	8	4	-3	-5
-2	-2 + 8 = +6
6
0
-4

Solution:

+	8	4	-3	-5
-2	(-2) + (+8) = +6	(-2) +(+4) = 2	(-2) +(-3) =-5	(-2) +(-5) =-7
6	(+6) + (+8) = 14	(+6) + (+4) = 10	(+6) + (-3) = 3	(+6) + (-5) = 1
0	0 + (+8) = 8	0 + (+4) = 4	0 + (-3) = -3	0 + (-5) = -5
-4	(-4) + (+8) = 4	(-4) +(+4) = 0	(-4) + (-3) = -7	(-4) + (-5) = -9

Maharashtra Board Class 6 Maths Chapter 3 Integers Practice Set 5 Intext Questions and Activities

Question 1.
On the playground, mark a timeline showing the years from 2000 to 2024. With one child standing at the position of the 2017, ask the following questions: (Textbook pg. no. 15)

1. While playing this game, what is his/her age?
2. Five years ago, which year was it? And what was his / her age then?
3. In which year will he / she go to Std X? How old will he / she be then?

The child should find answers to such questions by walking the right number of units and in the right direction on the timeline.
[Assume child born year is 2009]
Solutions:

1. Age of child is 8 years.
2. Five years ago, year was 2012. His/her age is 3 years.
3. In 2024, he/she will go the Std X. His/her age is 15 years.

Question 2.
On a playground mark a timeline of 100 years. This will make it possible to count the years from 0 to 2100 on it. Important historical events can then be shown in proper centuries. (Textbook pg. no. 16)
Solution:
(Students should attempt this activity on their own)

Question 3.
Observe the figures and write appropriate number in the boxes given below. (Textbook pg. no. 16 and 17)
i.

a. At first the rabbit was at the number ____
b. It hopped ___ units to the right.
c. It is now at the number ___
Solution:
i.
a. +1
b. 5
c. +6

ii.

a. At first the rabbit was at the number ___
b. It hopped ____ units to the right.
c. It is now at the number ____
Solution:
ii.
a. -2
b. 5
c. +3

iii.

a. At first the rabbit was at the number ___
b. It hopped ____ units to the left.
c. It is now at the number ___
Solution:
iii.
a. -3
b. 4
c. -7

iv.

a. At first the rabbit was at the number ___
b. It hopped___units to the left.
c. It is now at the number ____
Solution:
iv.
a. +3
b. 4
c. -1