Balbharti Maharashtra Board Class 5 Maths Solutions Chapter 9 Decimal Fractions Problem Set 40 Textbook Exercise Important Questions and Answers.
Maharashtra State Board Class 5 Maths Solutions Chapter 9 Decimal Fractions Problem Set 40
Write the following fractions as decimal fractions.
(1) Two and a half
Answer:
2 \(\frac{1}{2}\) = 2.5 = 2.50
![]()
(2) Two and a quarter
Answer:
2 \(\frac{1}{4}\) = 2.25
(3) Two and three quarters
Answer:
2 \(\frac{3}{4}\) = 2.75
(4) Ten and a half
Answer:
10 \(\frac{1}{2}\) = 10.5 = 10.50
(5) Fourteen and three quarters
Answer:
14 \(\frac{3}{4}\) = 14.75
(6) Sixteen and a quarter
Answer:
16 \(\frac{1}{4}\) = 16.25
![]()
(7) Twenty-eight and a half
Answer:
28 \(\frac{1}{2}\) = 28.50 = 28.5
Adding decimal fractions
Sir : If the cost of one pencil is two and a half rupees and the cost of a pen is four and half rupees, what is the total cost?
Sumit : Two and a half rupees means two rupees and one half rupee. Similarly, four and a half rupees means four rupees and one-half rupee. 4 rupees and 2 rupees make 6 rupees and two half rupees make one rupee, so both objects together cost 6 + 1 = 7 rupees.
Sir : Correct ! Now, see how this is done using decimals.
The sum of the 0’s in the hundredths place is 0.
0.5 + 0.5 is the same as
\(\frac{5}{10}+\frac{5}{10}=\frac{5+5}{10}=\frac{10}{10}=\frac{1}{1}=1\)
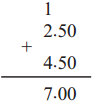
This 1 is carried over to the units place. There is nothing in the tenths place, so we put a zero there. In the units place, 2 + 4 = 6 plus the carried over 1 makes 7.
![]()
So 2.50 rupees and 4.50 rupees add up to 7 rupees.
We use the decimal system to write whole numbers. We extend the same method to write fractions; therefore, we can add in the same way as we add whole numbers.
I will now show some more additions. Watch carefully.
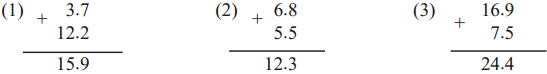
Sumit : There is no carried over number in the first sum, but there are carried over numbers in the second and third sums.
Rekha : While adding whole numbers, we add units first. Similarly, here, tenths are added first. In the second example, the sum of the tenths place is 13. 13 tenths are 10 tenths + 3 tenths = 1 unit + 3 tenths.
Sumit : That is why, in the sum, 3 stayed in the tenths place and 1 was carried over to the units place. 6 + 5 plus 1 carried over makes 12.
Sir : Your observations are absolutely correct. We write digits one below the other according to their place values while adding whole numbers. We do the same thing here. Remember that while writing down an addition problem and the total, the decimal points should always be written one below the other.
![]()
Study the following additions. (Note that: 10 tenths = 1 unit. 10 hundredths = 1 tenth)
Example (1) Add : 7.09 + 54.93
First, add the digits in the 100ths place. 9 + 3 = 12.
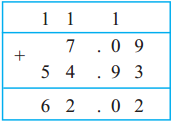
The 1 from the sum 12 in the hundredths place is carried over to the tenths place and 2 is written in the hundredths place. Adding 1 + 9 gives 10 tenths or 1 unit. This 1 is carried over to the units place. 0 is left in the tenths place. Then, the addition is completed in the usual way.
Example (2) Add : 45.83 + 167.4
4 5 . 8 3 We arrange the numbers so that the places and
+
1 6 7. 4 decimal points come one below the other.
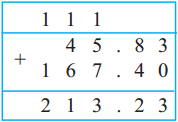
\(\frac{4}{10}=\frac{4 \times 10}{10 \times 10}=\frac{40}{100}\) Therefore, to make the denominators of the fractions equal, 167.4 is written as 167.40 and then the fractions are added.
![]()
As usual, the digits with the smallest place values are added first and then those with bigger place values are added serially.
Example (3) 10.46 Rupees
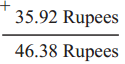
Example (4) 48.80 m
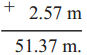
Example (5) 7.5 cm

Decimal Fractions Problem Set 40 Additional Important Questions and Answers
(1) Thirty and a quarter
Answer:
30 \(\frac{1}{4}\) = 30.25
(2) Thirty and a half
Answer:
30 \(\frac{1}{2}\) = 30.50 = 30.5
![]()
(3) Thirty and three quarters
Answer:
30 \(\frac{3}{4}\) = 30.75