Maharashtra Board Class 11 Physics Important Questions Chapter 5 Gravitation

Balbharti Maharashtra State Board 11th Physics Important Questions Chapter 5 Gravitation Important Questions and Answers.

Maharashtra State Board 11th Physics Important Questions Chapter 5 Gravitation

Question 1.
Mention some main characteristics of gravitational force.
Answer:
Characteristics of gravitational force:

1. Every massive object in the universe experiences a gravitational force.
2. It is the force of mutual attraction between any two objects by virtue of their masses.
3. It is always an attractive force with infinite range.
4. It does not depend upon the intervening medium.
5. It is much weaker than other fundamental forces. Gravitational force is 10 times weaker than the strong nuclear force.

Question 2.
State and explain Kepler’s law of orbits.
Answer:
Statement:
All planets move in elliptical orbits around the Sun with the Sun at one of the foci of the ellipse.
Explanation:

1. The figure M shows the orbit of a around the planet P Sun.
   
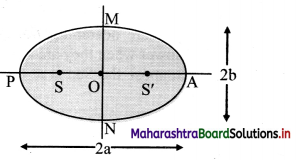
2. Here, S and S’ are the foci of the ellipse and the Sun is situated at S.
3. P is the closest point along the orbit from S and is called perihelion.
4. A is the farthest point from S and is called aphelion.
5. PA is the major axis whose length is 2a. PO and AO are the semimajor axes with lengths ‘a’ each.
   MN is the minor axis whose length is 2b. MO and ON are the semiminor axes with lengths ‘b’ each.

Question 3.
State and prove Kepler’s law of equal areas.
Answer:
Statement:

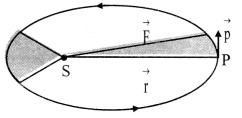
The line that joins a planet and the Sun sweeps equal areas in equal intervals of time.
Explanation:
i)Kepler observed that planets move faster when they are nearer to the Sun while they move slower when they are farther from the Sun.

ii) Suppose the Sun is at the origin. The position of planet is denoted by \(\vec{r}\) and its momentum is denoted by \(\vec{p}\) (component ⊥ \(\vec{r}\)).

vi) For central force the angular momentum is conserved. Hence, from equations (4) and (5),
\(\frac{\overrightarrow{\Delta \mathrm{A}}}{\Delta \mathrm{t}}=\frac{\overrightarrow{\mathrm{L}}}{2 \mathrm{~m}}\) = constant
This proves the law of areas.

Question 4.
What is a central force?
Answer:
A central force on an object is a force which is always directed along the line joining the position of object and a fired point usually taken to the origin of the coordinate system.

Question 5.
State and explain Kepler’s law of periods.
Answer:
Statement:
The square of the time period of revolution of a planet around the Sun is proportional to the cube of the semimajor axis of the ellipse traced by the planet.
Explanation:
If r is length of semi major axis then, this law states that.
T² × r³ or \(\frac{\mathrm{T}^{2}}{\mathrm{r}^{3}}\) = constant

Solved Examples

Question 6.
What would be the average duration of year if the distance between the Sun and the Earth becomes
i) thrice the present distance.
ii) twice the present distance.
Solution:
i) Consider r₁ be the present distance between the Earth and Sun
We know, T₁ = 365 days.
When the distance is made thrice, r₂ = 3r₁
According to Kepler’s law of period,

i) The duration of the year would be 1897 days when distance is made thrice.
ii) The duration of the year would be 1032 days when distance is made twice.

Question 7.
What would have been the duration of the year if the distance between the Earth and the Sun were half the present distance?
Solution:
Given: r₂ = \(\frac{\mathrm{r}_{1}}{2}\)
∴ \(\frac{r_{2}}{r_{1}}=\frac{1}{2}\)
To find. Time period (T₂)
Formula: \(\left(\frac{T_{2}}{T_{1}}\right)^{2}=\left(\frac{r_{2}}{r_{1}}\right)^{3}\)
Calculation: We know. T₁ = 365 days
From formula,

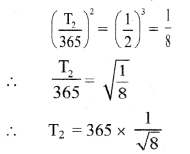
= 365 × 0.3536
= 129.1
T₂ = 129.1 days
The duration of the year would be 129.1 days.

Question 8.
Calculate the period of revolution of Jupiter around the Sun. The ratio of the radius of Jupiter’s orbit to that of the Earth’s orbit is 5.
(Period of revolution of the Earth is 1 year.)
Solution:
Given: \(\frac{\mathrm{r}_{\mathrm{J}}}{\mathrm{r}_{\mathrm{E}}}=\frac{5}{\mathrm{l}}\), T_E = 1 year
To find: Period of revolution of Jupiter (T_J)
Formula: T² ∝ r³
Calculation: From formula,
\(\left(\frac{T_{J}}{T_{E}}\right)^{2}=\left(\frac{r_{J}}{r_{E}}\right)^{3}\)
∴ T_J = 5^3/2
= 5 x \(\sqrt {5}\)
= 11.18 years.
Period of revolution of Jupiter around the Sun is 11.18 years.

Question 9.
A Saturn sear is 29.5 times the Earth’s year. How far is the Saturn from the Sun if the Earth is 1.50 × 10⁸ km away from the Sun?
Solution:
Given: T_S = 29.5 T_E,
r_E = 1.50 × 10⁸ km
To find: Distance of Saturn form the Sun (r_S)
Formula: T² ∝ r³
Calculation: From formula,

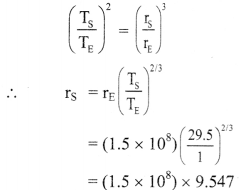
∴ r_S = 14.32 × 10⁸ km
Saturn is 14.32 × 10⁸ km away from the Sun.

Question 10.
The distances of two planets from the Sun are 10¹³ m and 10¹² m respectively. Find the ratio of time periods of the two planets.
Solution:
Given: r₁ = 10¹³ m, r₂ = 10¹² m

Question 11.
Heavy and light objects are released from same height near the Earth’s surface. What can we conclude about their acceleration?
Answer:
Heavy and light objects, when released from the same height, fall towards the Earth at the same speed., i.e., they have the same acceleration.

Question 12.
Explain how Newton concluded that gravitational force F ∝ = \(\frac{\mathrm{Mm}}{\mathrm{r}^{2}}\)
Answer:
Before generalising and stating universal law of gravitation, Newton first studied the motion of moon around the Earth.

1. The known facts about the moon were,
   • the time period of revolution of moon around the Earth (T) = 27.3 days.
   • distance between the Earth and the moon (r) = 3.85 × 10⁵ km.
   • the moon revolves around the Earth in almost circular orbit with constant angular velocity ω.
2. Thus, the centripetal force experienced by moon (directed towards the centre of the Earth) is given by,
   F = mrω² …………… (1)
   Where, m = mass of the moon
3. From Newton’s laws of motion,
   F = ma
   ∴ a = rω² ……………… (2)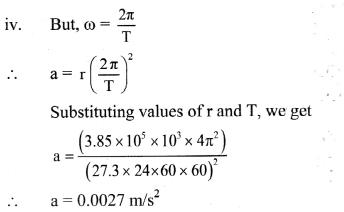
4. 
5. This is the acceleration of the moon directed towards the centre of the Earth.
6. This acceleration is much smaller than the acceleration felt by bodies near the surface of the Earth (while falling on Earth).
7. The value of acceleration due to Earth’s gravity at the surface is 9.8 m/s².
   
8. Newton therefore concluded that the acceleration of an object towards the Earth is inversely proportional to the square of distance of object from the centre of the Earth.
   ∴ a ∝ \(\frac{1}{r^{2}}\)
   x. As, F = ma
   Therefore, the force exerted by the Earth on an object of mass m at a distance r from it is
   F ∝ \(\frac{\mathrm{m}}{\mathrm{r}^{2}}\)
   Similarly, an object also exerts a force on the Earth which is
   F_E ∝ \(\frac{\mathrm{M}}{\mathrm{r}^{2}}\)
   Where M is the mass of the Earth. .
9. According to Newton’s third law of motion, F = F_E. Thus, F is also proportional to the mass of the Earth. From these observations, Newton concluded that the gravitational force between the Earth and an object of mass m is F ∝ \(\frac{\mathrm{Mm}}{\mathrm{r}^{2}}\)

Question 13.
Discuss the vector form of gravitational force between two masses with the help of diagram.
Answer:

1. Consider two point masses m₁ and m₂ having position vectors \(\overrightarrow{\mathrm{r}_{1}}\) and \(\overrightarrow{\mathrm{r}_{2}}\) from origin O respectively as shown in figure.
   
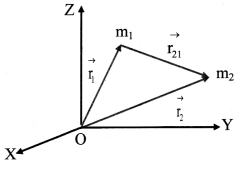
2. The position vector of mass m₂ with respect to m₁ is given by, \(\vec{r}_{2}-\vec{r}_{1}=\vec{r}_{21}\)
3. Similarly, position vector of mass m₁ with respect to m₂ is, \(\overrightarrow{\mathrm{r}}_{1}-\overrightarrow{\mathrm{r}_{2}}=\overrightarrow{\mathrm{r}_{12}}\)
4. Let \(\left|\overrightarrow{\mathrm{r}_{12}}\right|=\left|\overrightarrow{\mathrm{r}_{21}}\right|\) Then, the force acting on mass m₂ due to mass m₁ will be given as,
   \(\overrightarrow{\mathrm{F}_{21}}=\mathrm{G} \frac{\mathrm{m}_{1} \mathrm{~m}_{2}}{\mathrm{r}^{2}}\left(-\hat{\mathrm{r}}_{21}\right)\)
   where, \(\hat{\mathbf{r}}_{21}\) is the unit vector from m₁ to m₂.
   The force \(\overrightarrow{\mathrm{F}_{21}}\) is directed from m₂ to m₁.
5. Similarly, force experienced by m₁ due to m₂ is given as, \(\overrightarrow{\mathrm{F}}_{12}=\mathrm{G} \frac{\mathrm{m}_{1} \mathrm{~m}_{2}}{\mathrm{r}^{2}}\left(-\hat{\mathrm{r}}_{12}\right)\)
   ∴ \(\overrightarrow{\mathrm{F}}_{12}=-\overrightarrow{\mathrm{F}}_{21}\)
   [Note: As \(\hat{\mathbf{r}}_{21}\) is defined as unit vector from m₁ to m₂, conceptually force \(\overrightarrow{\mathrm{F}}_{21}\) is directed from m₂ lo m₁.]

Question 14.
Why Is the law of gravitation known as universal law of gravitation?
Answer:
The law of gravitation is applicable to all material objects in the universe. Hence it is known as the universal law of gravitation.

Question 15.
Give formula for the gravitational force due to a collection of masses and represent it diagrammatically.
Answer:

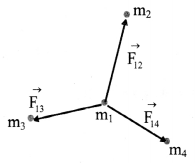
For a collection of point masses, the force on any one of them is the vector sum of the gravitational forces exerted by all the other point masses.
For n particles, force on i^th mass \(\overrightarrow{\mathrm{F}}_{\mathrm{i}}=\sum_{\mathrm{j}=1 \atop \mathrm{j} \neq \mathrm{i}}^{n} \overrightarrow{\mathrm{F}}_{\mathrm{ij}}\)
where, \(\vec{F}_{\mathrm{ij}}\) is the force on i^th particle due to j^th particle.

Question 16.
Discuss qualitative idea for the gravitational force of attraction due to a hollow, thin spherical shell of uniform density on a point mass situated inside it.
Answer:

1. Let us consider the case when the point mass A, is at the centre of the hollow thin shell.
2. In this case as every point on the shell is equidistant from A, all points exert force of equal magnitude on A but the directions of these forces are different.
3. Consider the forces on A due to two diametrically opposite points on the shell.
4. The forces on A due to them will be of equal magnitude but will be in opposite directions and will cancel each other.
5. Thus, forces due to all pairs of points diametrically opposite to each other will cancel and there will be no net force on A due to the shell.
6. When the point object is situated elsewhere inside the shell, the situation is not symmetric. However, gravitational force varies directly with mass and inversely with square of the distance.
7. When the point object is situated elsewhere inside the shell, the situation is not symmetric. However, gravitational force varies directly with mass and inversely with square of the distance.
8. Thus, some part of the shell may be closer to point A, but its mass is less. Remaining part will then have larger mass but its centre of mass is away from A.
9. In this way, mathematically it can be shown that the net gravitational force on A is still zero, so long as it is inside the shell.
10. Hence, the gravitational force at any point inside any hollow closed object of any shape is zero.

Question 17.
Discuss qualitative idea for the gravitational force of attraction between a hollow spherical shell or solid sphere of uniform density and a point mass situated outside the shell / sphere.
Answer:

• Gravitational force caused by different regions of shell can be resolved into components along the line joining the point mass to the centre and along a direction perpendicular to this line.
• The components perpendicular to this line cancel each other and the resultant force remains along the line joining the point to the centre.
• Mathematical calculations show that, this resultant force on this point equals the force that would get exerted by the shell whose entire mass is situated at its centre.

Solved Problems

Question 18.
The gravitational force between two bodies is 1 N. If distance between them is doubled, what will be the gravitational force between them?
Solution:
Let m₁ and m₂ be masses of the given two bodies. If they are r distance apart initially, then the force between them will be,

The force between two bodies reduces to 0.25 N.

Question 19.
Calculate the force of attraction between two metal spheres each of mass 90 kg, if the distance between their centres is 40 cm. (G = 6.67 × 10^-11 N m²/kg²)
Solution:
Given: m₁ = 90 kg, m₂ = 90 kg,
r = 40 cm = 40 × 10^-2 m.
G = 6.67 × 10^-11 N m²/kg²
To find: Force of attraction (F)
Formula: F = \(\frac{\mathrm{Gm}_{1} \mathrm{~m}_{2}}{\mathrm{r}^{2}}\)
Calculation.
From formula,
F = \(\frac{6.67 \times 10^{-11} \times 90 \times 90}{\left(40 \times 10^{-2}\right)^{2}}\)
= \(\frac{6.67 \times 8100}{1600} \times 10^{-7}\)
∴ F = 3.377 × 10^-6 N
The force of attraction between the two metal spheres is 3.377 × 10^-6 N.

Question 20.
Three particles A, B, and C each having mass m are kept along a straight line with AB = BC = 1. A fourth particle D is kept on the perpendicular bisector of AC at a distance ¡ from B. Determine the gravitational force on D.
Solution:

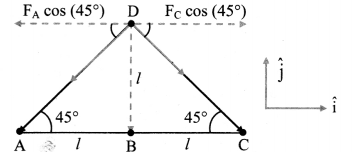
From figure,
distance of particle D, from particles A and C is.
ADCD = \(\sqrt{\mathrm{AB}^{2}+\mathrm{BD}^{2}}\)
= \(\sqrt{(l)^{2}+(l)^{2}}=l \sqrt{2}\)
Gravitational force on particle D is the vector sum of forces due to particles A, B, and C. Gravitational force due to A,
F_A = \(\frac{\mathrm{Gmm}}{(l \sqrt{2})^{2}}=\frac{\mathrm{Gm}^{2}}{2 l^{2}}\) = along \(\overrightarrow{\mathrm{DA}}\)
This force can he resolved into horizontal and vertical components using rectangular unit vectors as shown in figure.
From figure,


Negative sign indicates net force is acting along DB.
The net force acting on particle D is \(\frac{\mathbf{G m}^{2}}{l^{2}}\left(\frac{1}{\sqrt{2}}+1\right)\) directed along \(\overrightarrow{\mathbf{D B}}\).

[Note: When force, in given case is resolved into its components, its horizontal component contains cos argument while vertical component contains sine argument.]

Question 21.
Three balls of masses 5 kg each are kept at points P(1, 2, 0) Q(2, 3, 0) and R(2, 2, 0). Find the gravitational force exerted on the ball at point R.
Solution:
The net force acting on ball placed at R will be vector sum of forces acting due to balls at P and Q.

= 2.358 × 10^-9 N
The net force acting on the ball at point R will be 2.358 × 10^-9 N.

Question 22.
For what purpose Cavendish balance is used?
Answer:
Cavendish balance is used to find the magnitude of the gravitational constant G.

Question 23.
Describe the construction of Cavendish balance with the help of neat labelled diagram.
Answer:

1. The Cavendish balance consists of a light rigid rod. It is supported at the centre by a fine vertical metallic fibre about 100 cm long.
2. Two small spheres, s₁ and s₂ of lead having equal mass m and diameter about 5 cm are mounted at the ends of the rod and a small mirror M is fastened to the metallic fibre as shown in figure.
   
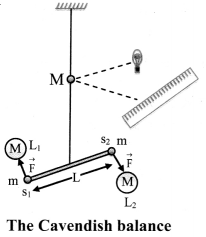
3. The mirror can be used to reflect a beam of light onto a scale and thereby measure the angel through which the wire will be twisted.
4. Two large lead spheres L₁ and L₂ of equal mass M and diameter of about 20 cm are kept close to the small spheres on opposite side as shown in figure.

Question 24.
Describe the working of the experiment performed to measure the value of gravitational constant.
Answer:

1. In the experiment performed to find the magnitude of gravitational constant (G), Cavendish balance is used.
2. The large spheres in the balance attract the nearby smaller spheres by equal and opposite force \(\overrightarrow{\mathrm{F}}\). Hence, a torque is generated without exerting any net force on the bar.
3. Due to the torque the bar turns and the suspension wire gets twisted till the restoring torque due to the elastic property of the wire becomes equal to the gravitational torque.
4. If r is the initial distance of separation between the centres of the large and the neighbouring small sphere, then the magnitude of the force between them is, F = G\(\frac{\mathrm{mM}}{\mathrm{r}^{2}}\)
5. If length of the rod is L, then the magnitude of the torque arising out of these forces is
   τ = FL = G\(\frac{\mathrm{mM}}{\mathrm{r}^{2}}\)L
6. At equilibrium, it is equal and opposite to the restoring torque.
   ∴ G\(\frac{\mathrm{mM}}{\mathrm{r}^{2}}\)L = Kθ
   Where, K is the restoring torque per unit angle and θ is the angle of twist.
7. By knowing the values of torque τ₁ it and corresponding angle of twist a, the restoring torque per unit twist can be determined as K = τ₁/α.
8. Thus, in actual experiment measuring θ and knowing values of τ, m, M and r, the value of G can be calculated from equation (2).

Question 25.
Derive the expression for the acceleration due to gravity on the surface of the Earth.
Answer:

1. The Earth is an extended object and can be assumed to be a uniform sphere.
2. If the mass of the Earth is M and that of any point object is m, the distance of the point object from the centre of the Earth is r then the force of attraction between them is given by,
   F = \(\text { G } \frac{M m}{r^{2}}\) …. (1)
3. If the point object is not acted upon by any other force, it will be accelerated towards the centre of the Earth under the action of this force. Its acceleration can be calculated by using Newton’s second law,
   F = ma … (2)
4. From equations (1) and (2),
   ma = \(\frac{\mathrm{GMm}}{\mathrm{r}^{2}}\)
   ∴ Acceleration due to the gravity of the Earth
   \(=\frac{\mathrm{GMm}}{\mathrm{r}^{2}} \times \frac{1}{\mathrm{~m}}=\frac{\mathrm{GM}}{\mathrm{r}^{2}}\)
   This is denoted by g.
5. If the object is close to the surface of the Earth, r ≈ R, then,
   g_{Earth’s surface} = \(\frac{\mathrm{GM}}{\mathrm{R}^{2}}\)

Question 26.
Explain why the Earth doesn’t appear to move even though the object of mass m (m << M) kept on the Earth exerts equal and opposite gravitational force on it.
Answer:

1. An object of mass m (much smaller than the mass of the Earth) is attracted towards the Earth and falls on it.
2. At the same time, the Earth is also attracted by the equal and opposite force towards the mass m.
3. However, its acceleration towards m will be,
   
4. As m << M, a_Earth << g and is nearly zero. As, a result, practically only the mass m moves towards the Earth and the Earth doesn’t appear to move.

Solved Examples

Question 27.
Calculate mass of the Earth from given data, Acceleration due to gravity g = 9.81 m/s², Radius of the Earth R_E = 6.37 × 10⁶ m, G = 6.67 × 10^-11 N m²/kg²
Solution:
Given: g = 9.81 m/s², R_E = 6.37 × 10⁶ m,
G = 6.67 × 10^-11 N m²/kg²
To find: Mass of the Earth (M_E)
Formula: g = \(\frac{\mathrm{GM}_{\mathrm{E}}}{\mathrm{R}_{\mathrm{E}}^{2}}\)
Calculation: From formula,

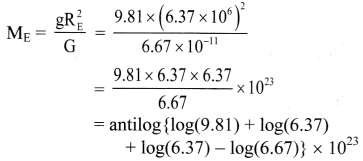
= antilog {0.9912 + 0.8041 + 0.8041 – 0.8241) × 10²³
= antilog {1.7753} × 10²³
= 59.61 × 10²³
= 5.961 × 10²⁴ kg
Mass of the Earth is 5.961 × 10²⁴ kg.

Question 28.
Calculate the acceleration due to gravity at the surface of the Earth from the given data. (Mass of the Earth = 6 × 10²⁴ kg, Radius of the Earth = 6.4 × 10⁶ m, G = 6.67 × 10^-11 N m²/kg²)
Solution:
Given. M = 6 × 10²⁴ kg, R = 6.4 × 10⁶ m, G = 6.67 × 10^-11 N m²/kg²
Tofind. Acceleration due to gravity (g)
Formula: g = \(\frac{\mathrm{GM}}{\mathrm{R}^{2}}\)
Calculation: From formula,

The acceleration due to gravity at the surface of the Earth is 9.77 m/s².

Question 29.
Calculate the acceleration due to gravity on the surface of moon if mass of the moon is 1/80 times that of the Earth and diameter of the moon is 1/4 times that of the Earth (g = 9.8 m/s²)
Solution:
Given: M_m = \(\frac{\mathrm{M}_{\mathrm{E}}}{80}\), R_m = \(\frac{\mathrm{R}_{\mathrm{E}}}{4}\), g = 9.8 m/s²
To find: Acceleration due to gravity on the surface of moon (g_m)
Formula: g = \(\frac{\mathrm{GM}}{\mathrm{R}^{2}}\)
Calculation: For moon, from formula,

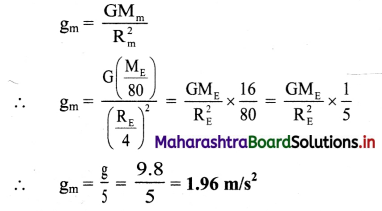
Acceleration due to gravity on surface of the planet is 0.245 m/s².

Question 30.
Find the acceleration due to gravity on a planet that is 10 times as massive as the Earth and with radius 20 times of the radius of the Earth (g = 9.8 m/s²).
Solution:
Given: M_P = 10 × Mass of the Earth = 10 M_E,
R_P = 20 × radius of the Earth = 20 R_E, g = 9.8 m/s²
To find: Acceleration due to gravity on surface of the planet (g_P)
Formula: g = \(\frac{\mathrm{GM}}{\mathrm{R}^{2}}\)
Calculation: From formula,

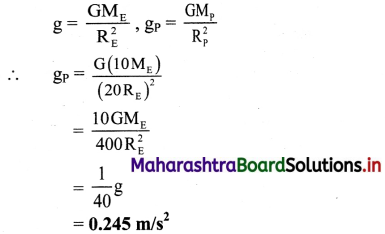
Acceleration due to gravity on surface of the planet is 0.245 m/s².

Question 31.
Acceleration due to gravity on the Earth is g. A planet has mass and radius half that of the Earth. How much will be percentage change in the acceleration due to gravity on the planet?
Solution:

The percentage change in acceleration due to gravity between the planet and the Earth will be 100%.

Question 32.
Explain the graph showing variation of acceleration due to gravity with altitude and depth.
Answer:
The value of acceleration due to gravity is calculated to be maximum at the surface of the Earth. The value goes on decreasing with
i) increase in depth below the Earth’s surface. [varies linearly with (R – d) = r]

ii) increase in height above the Earth’s surface. [varies inversely with (R + h)² = r²].

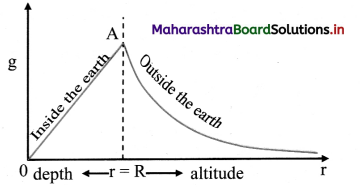
Graph of g, as a function of r, the distance from the centre of the Earth, is plotted as shown in figure.
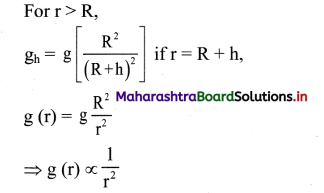
For r< R,
g_d = g\(\left(1-\frac{\mathrm{d}}{\mathrm{R}}\right)\)
if r = R – d,
g(r) = g\(\left(\frac{r}{R}\right) \Rightarrow g(r) \propto r\)
Hence, the graph shows a straight line passing through origin and having slope \(\frac{\mathrm{g}}{\mathrm{R}}\).

which is represented in the graph.

Question 33.
Why does the weight of a body of a finite mass m is zero at the centre of the Earth?
Answer:
Acceleration at depth d due to gravity is given
by,
g_d = g\(\left(1-\frac{\mathrm{d}}{\mathrm{R}}\right)\)
As, at centre of the Earth d = R ⇒ g_d = 0.
Hence, the weight of a body of a finite mass m is zero at the centre of the Earth.

Question 34.
Discuss the variation of acceleration due to gravity at poles and equator due to latitude of the Earth.
Answer:

1. Effective acceleration due to gravity at P is given as,
   g’ = g – Rω²cos²θ.
2. As the value of θ increases, cos θ decreases. Therefore g’ will increase as we move away from equator towards any pole due to the rotation of the Earth.
3. At equator θ = 0°
   ∴ cos θ = 1
   ∴ g’_e = g – Rω²
   The effective acceleration due to gravity (g’_e) is minimum at equator, as here it is reduced by Rω²
4. At poles θ = 90° cos θ = 0
   ∴ g’_p = g – Rω² cos θ
   = g – 0
   = g
   There is no reduction in acceleration due to gravity at poles, due to the rotation of the Earth as the poles are lying on the axis of rotation and do not revolve.

Question 35.
If g = 9.8 m/s² on the surface of the Earth, find its value at h = \(\frac{\mathbf{R}}{\mathbf{2}}\) from the surface of the Earth.
Solution:
Given: g = 9.8 m/s², h = \(\frac{\mathrm{R}}{2}\)
To find: Acceleration due to gravity (g_h)
Formula: \(\frac{\mathrm{g}_{\mathrm{h}}}{\mathrm{g}}\) = \(\frac{\mathrm{R}^{2}}{(\mathrm{R}+\mathrm{h})^{2}}\)
Calculation:
From formula,

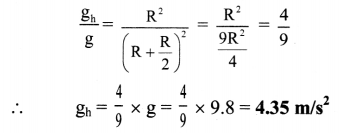
At h = \(\frac{\mathrm{R}}{2}\) from the surface of the Earth, the value of g is 4.35 m/s².

Question 36.
At what distance above the surface of Earth the acceleration due to gravity decreases by 10% of its value at the surface? (Radius of Earth = 6400 km)
Solution:
Given: g_h = 90% of g i.e., \(\frac{g_{h}}{g}\) = 0.9,
R = 6400 km = 6.4 × 10⁶ m
To find: Distance above the surface of the Earth (h)

Question 37.
Find the altitude at which the acceleration due to gravity is 25% of that at the surface of the Earth.
(Radius of the Earth = 6400 km)
Solution:
Given: g_h = 25% of g = \(\frac{25}{100} \times \mathrm{g}=\frac{\mathrm{g}}{4}\), R = 6400 km = 6.4 × 10⁶ m
To find: Height (h)
Formula: g_h = g\(\left(\frac{R}{R+h}\right)^{2}\)
Calculation: From formula,
\(\frac{\mathrm{g}}{4}\) = g\(\left(\frac{R}{R+h}\right)^{2}\)
(R + h)² = 4R²
R + h = 2R
∴ h = 2R – R
∴ h = R
∴ h = 6400 km

Question 38.
A hole is drilled half way to the centre of the Earth. A body is dropped into the hole. How much will it weigh at the bottom of the hole if the weight of the body on the Earth’s surface is 350 N?
Solution:
Given: W = mg = 350 N, d = \(\frac{\mathrm{R}}{2}\)
To find: Weight at certain depth (W_d)
Formula: g_d = \(\mathrm{g}\left[1-\frac{\mathrm{d}}{\mathrm{R}}\right]\)
Calculation: Since W_d = mg_d,
from formula,

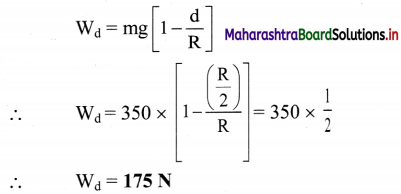
Question 39.
Assuming the Earth to be a homogeneous sphere, determine the density of the Earth from following data. (g = 9.8 m/s², G = 6.673 × 10^-11 N m²/kg², R = 6400 km)
Solution:
Given g = 9.8 m/s²,
G = 6.673 × 10^-11 N m²/kg², R = 6400 km = 6.4 × 10⁶ m
To find: Density (ρ)
Formula: g = \(\frac{4}{3} \pi \mathrm{R} \rho \mathrm{G}\)
Calculation: From formula,

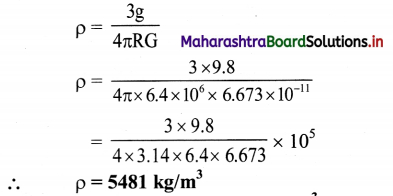
Question 40.
If the Earth were a perfect sphere of radius 6.4 × 10⁶ m rotating about its axis with the period of one day (8.64 × 10⁴ s), what is the difference in acceleration due to gravity from poles to equator?
Solution:
Given: R = 6.4 × 10⁶ m, T = 8.64 × 10⁴ s
To find: Difference in acceleration due to gravity (g_P – g_E)
Formula: g’ = g – Rω² cos²θ
Calculation: Since ω = \(\frac{2 \pi}{\mathrm{T}}\)
∴ ω = \(\frac{2 \times 3.14}{8.64 \times 10^{4}}\) = \(\frac{6.28}{8.64 \times 10^{4}}\)
= 0.7268 × 10^-4
ω = 7.268 × 10^-5 rad/s
At poles, θ = 90°
From formula,
g_P = g – Rω²cos² (90°)
= g – 0 ….(∵ cos 90° = 0)
∴ g_P = g …. (i)
At equator, θ = 0°,
∴ g_E = g – Rω²cos² 0°
g_E = g – Rω² …. (ii)
Subtracting equation (ii) from equation (i), we have,
g_P – g_E = g – (g – Rω²)
∴ g_P – g_E = Rω²
= 6.4 × 10⁶ × (7.268 × 10^-5)²
= 6.4 × 10⁶ × 52.82 × 10^-10
= 338 × 10^-4
∴ g_P – g_E = 3.38 × 10^-2 m/s²

Question 41.
The Earth is rotating with angular velocity ω about its own axis. R is the radius of the Earth. If Rω² = 0.03386 m/s², calculate the weight of a body of mass 100 gram at latitude 25°. (g = 9.8 m/s²)
Solution:
Given: Rω² = 0.03386 m/s², θ = 25°,
m = 0.1 kg, g = 9.8 m/s²
To find: Weight (W)

Formulae:
i) g’ = g – Rω² cos² θ
ii) W = mg

Calculation:
From formula (i),
g’ = 9.8 – [0.03386 – cos² (25°)]
∴ g’ = 9.8 – [0.03386 × (0.9063)²]
∴ g’ = 9.8 – 0.02781
∴ g’ = 9.772 m/s²
From formula (ii),
W = 0.1 × 9.772
∴ W = 0.9772 N

Question 42.
If the angular speed of the Earth is 7.26 × 10^-5 rad/s and radius of the Earth is 6,400 km, calculate the change in weight of 1 kg of mass taken from equator to pole.
Solution:
Given: R = 6.4 × 10⁶ m, ω = 7.26 × 10^-5 rad/s
To find: Change in weight (∆W)
Formulae:
i) ∆g = g_p – g_eq = Rω²
ii) ∆W = m∆g

Calculation: From formula (i) and (ii),
∆W = m(Rω²)
= 1 × 6.4 × 10⁶ × (7.26 × 10^-5)²
= 3373 × 10^-5 N

Question 43.
Define potential energy.
Answer:
Potential energy is the work done against conservative force (or forces) in achieving a certain position or configuration of a given system.

Question 44.
Explain with examples the universal law which states that “Every system always configures itself in order to have minimum potential energy or every system tries to minimize its potential energy”.
Answer:
Example 1:

1. A spring in its natural state, possesses minimum potential energy. Whenever we stretch it or compress it, we perform work against the conservative force.
2. Due to this work, the relative distances between the particles of the system change i.e., configuration changes and potential energy of the spring increases.
3. The spring finally regains its original configuration of minimum potential energy on removal of the applied force.
   This explains that the spring always try to rearrange itself in order to attain minimum potential energy.

Example 2:

1. When an object is lying on the surface of the Earth, the system of that object and the Earth has minimum potential energy.
2. This is the gravitational potential energy of the system as these two are bound by the gravitational force. While lifting the object to some height, we do work against the conservative gravitational force.
3. In its new position, the object is at rest due to balanced forces. However, now, the object has a capacity to acquire kinetic energy, when allowed to fall.
4. This increase in the capacity is the potential energy gained by the system. The object falls on the Earth to achieve the configuration of minimum potential energy on dropping it from the new position.

Question 45.
Obtain an expression for change in gravitational potential energy of any object displaced from one point to another.
Answer:
i) Work done against gravitational force in displacing an object through a small displacement, stored in the system in the form of increased potential energy of the system.
∴ dU = –\(\overrightarrow{\mathrm{F}}_{\mathrm{g}} \cdot \overrightarrow{\mathrm{dr}}\)
Negative sign appears because dU is the work done against the gravitational force \(\overrightarrow{\mathrm{F}_{\mathrm{g}}}\).

ii) For displacement of the object from an initial position \(\overrightarrow{\mathrm{r}_{\mathrm{i}}}\) to the final position \(\overrightarrow{\mathrm{r}_{\mathrm{f}}}\), the change in potential energy ∆U, can be obtained by integrating dU.

 

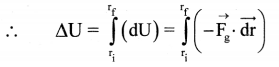
iii) Gravitational force of the Earth, \(\overrightarrow{\mathrm{F}}_{\mathrm{g}}\) = –\(\frac{\mathrm{GMm}}{\mathrm{r}^{2}} \hat{\mathrm{r}}\) where \(\hat{r}\) is the unit vector in the direction of \(\overrightarrow{\mathrm{r}}\).
Negative sign appears here because \(\overrightarrow{\mathrm{F}_{\mathrm{g}}}\) is directed towards centre of the Earth and opposite to \(\overrightarrow{\mathrm{r}}\).

iv) For Earth and mass system,

Hence, change in potential energy corresponds to the work done against conservative forces.

Question 46.
Using expression for change in potential energy, show that gravitational potential energy of the system of object of mass m and the Earth with separation of r is, –\(\frac{\text { GMm }}{\text { r }}\)
Answer:

1. Change in P.E. for a system of Earth and mass is given by,
   ∆U = GMm\(\left(\frac{1}{r_{i}}-\frac{1}{r_{f}}\right)\)
2. For gravitational force, point of zero potential energy is taken to be at r = ∞.
3. Hence, U(r_i) = 0 at r_i = ∞
   Final point r_f is the point where the potential energy of the system is to be determined.
4. At r_f = r
   
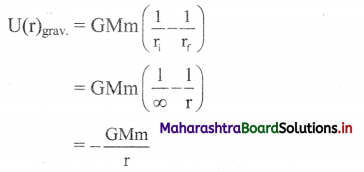
   This is gravitational potential energy of the system of object of mass m and Earth of mass M having separation r (between their centres of mass).

Question 47.
Derive the formula for increase in gravitational potential energy of a Earth – mass system when the mass is lifted to a height h provided h << R.
Answer:

1. If the object is on the surface of Earth, r = R
   U₁ = –\(\frac{\mathrm{GMm}}{\mathrm{R}}\)
   If the object is lifted to height h above the surface of Earth, the potential energy becomes _ GMm 12 ~~ R+h
   U₂ = –\(\frac{G M m}{R+h}\)
2. Increase in the potential energy is given by
   
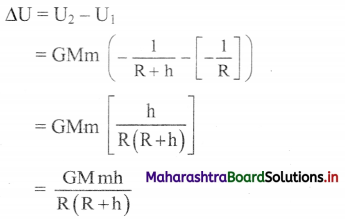
3. If g is acceleration due to gravity on the surface of Earth. GM = gR²
   ∴ ∆U = mgh\(\left(\frac{R}{R+h}\right)\) … (1)
4. Equation (1) gives the work to be done to raise an object of mass rn to a height h, above the surface of the Earth.
5. If h << R, we can use R + h ≈ R.
   ∴ ∆U = mgh
   Thus, mgh is increase in the gravitational potential energy of the Earth – mass system if an object of mass m is lifted to a height h, provided h << R.

Question 48.
Write a short note on gravitational potential.
Answer:
The gravitational potential energy of the system of Earth and any mass m at a distance r from the centre of the Earth is given by,

The factor –\(\frac{\mathrm{GM}}{\mathrm{r}}\) = (V_E)_r is defined as the
gravitational potential of Earth at distance r from its centre.

As the potential depends only upon mass of the Earth and location of the object, it is same for any mass m bound to the Earth.

Question 49.
Explain the relation between the gravitational potential energy and the gravitational potential.
Answer:

1. In terms of potential, we can write the potential energy of the Earth-mass system as, Gravitational potential energy (U) = Gravitational potential (V_r) × mass (m)
2. Thus, gravitational potential is gravitational potential energy per unit mass.
   ∴ V_r = \(\frac{\mathrm{U}}{\mathrm{m}}\)
3. For any conservative force field, the concept of potential can be defined on similar lines.
4. Gravitational potential difference between any two points in gravitational field can be written as,
   V₂ – V₁ = \(\frac{U_{2}-U_{1}}{m}\)
   = \(\frac{\mathrm{dW}}{\mathrm{m}}\)
   This is the work done (or change in potential energy) per unit mass.
5. Therefore, in general, for a system of any two masses m₁ and m₂, separated by distance r, we can write,
   U = –\(\frac{\mathrm{G} \mathrm{m}_{1} \mathrm{~m}_{2}}{\mathrm{r}}\)
   = (V₁)m₂
   = (V₂)m₁
   Here V₁ and V₂ are gravitational potentials at r due to m₁ and m₂ respectively.

Solved Exmaples

Question 50.
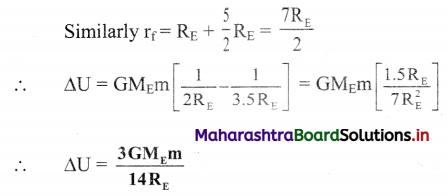
What will be the change in potential energy of a body of mass m when it is raised from height R_E above the Earth’s surface to 5/2 R_E above the Earth’s surface? R_E and M_E are the radius and mass of the Earth respectively.
Solution:
Change in potential energy (P.E.) of a body of mass m is given by,
∆U = GM_Em\(\left(\frac{1}{r_{i}}-\frac{1}{r_{f}}\right)\)
Here, r_i = R_E + R_E = 2 R_E

[Note: Answer calculated above is in accordance with textual methods of calculation.]

Question 51.
What will be the change in potential energy of a body of mass m when it is placed on the surface of the Earth from height R above the Earth’s surface?
Solution:
Change in potential energy (P.E.) of a body of mass m is given by,
∆U = GM_Em\(\frac{1}{r_{i}}-\frac{1}{r_{r}}\)
Here, r_i = R + R = 2R
Similarly, r_f = R
∴ ∆U = GM_Em \(\left[\frac{1}{2 R}-\frac{1}{R}\right]\) = GM_Em\(\left(-\frac{1}{2 R}\right)\)
∴ ∆U = –\(\frac{\mathbf{G} \mathbf{M} \mathbf{m}}{\mathbf{2 R}}\)
Negative sign indicates that potential energy is decreasing.

Question 52.
Determine the gravitational potential of a body of mass 80 kg whose gravitational potential energy is 5 × 10⁹ J on the surface of the Earth.
Solution:
Given: m = 80 kg, U = 5 × 10⁹ J
To find: Gravitational potential (V)
Formula: V = \(\frac{\mathrm{U}}{\mathrm{m}}\)
Calculation: From formula,
V = \(\frac{5 \times 10^{9}}{80}=\frac{25}{4}\) × 10⁷
= 6.25 × 10⁷ J kg^-1
Potential of the body at the surface of the Earth is 6.25 × 10⁷ J kg^-1.

Question 53.
Calculate the escape velocity of a body from the surface of the Earth.
(Average density of Earth = 5.5 × 10³ kg/m³, G = 6.67 × 10^-11 N m²/kg², radius of Earth R = 6.4 × 10⁶ m)
Solution:
Given: ρ = 5.5 × 10³ kg/m³, R = 6.4 × 10⁶ m,
G = 6.67 × 10^-11 N m²/kg²
To find: Escape velocity (v_e)

= 2 × 6.4 × 10⁶ × 8.759 × 10^-4
∴ v_e = 11.21 × 10³ m/s = 11.21 km/s
The escape velocity of a body is 11.21 km/s.

Question 54.
What is a satellite?
Answer:
An object which revolves in an orbit around a planet is called as satellite.
Example:

• Moon is a natural satellite of the Earth.
• INSAT is an artificial satellite of the Earth.

Question 55.
Write a short note on Polar satellites.
Answer:

1. Polar Satellites are placed in lower polar orbits.
2. They are at low altitude 500 km to 800 km.
3. Period of revolution of polar satellite is nearly 85 minutes, so it can orbit the Earth 16 time per day.
4. They go around the poles of the Earth in a north-south direction while the Earth rotates in an east-west direction about its own axis.
5. The polar satellites have cameras fixed on them. The camera can view small stipes of the Earth in one orbit. In entire day the whole Earth can be viewed strip by strip.
6. Polar region and equatorial regions close to it can be viewed by these satellites.
7. Polar satellites are used for weather forecasting and meteorological purpose. They are also used for astronomical observations and study of Solar radiations.

Question 56.
Derive the expression for the critical velocity of a satellite revolving close to the surface of the Earth in terms of acceleration due to gravity.
Answer:

1. When the satellite is revolving close to the surface of the Earth, the height is very small as compared to the radius of the Earth.
2. Hence the height can be neglected and radius of the orbit is nearly equal to R, i.e., R + h ≈ R
3. The critical speed of the satellite then becomes,
   v_c = \(\sqrt{\frac{G M}{R}}\)
4. G is related to acceleration due to gravity by the relation,
   g = \(\frac{G M}{R^{2}}\)
   ∴ GM = gR²
5. Thus, critical speed in terms of acceleration due to gravity, neglecting the air resistance, can be obtained as,
   v_c = \(\sqrt{\frac{\mathrm{gR}^{2}}{\mathrm{R}}}=\sqrt{\mathrm{gR}}\)

Question 57.
From an inertial frame of reference, explain the apparent weight for a person standing in a lift having zero acceleration.
Answer:

1. A passenger inside a lift experiences only two forces:
   • Gravitational force mg directed vertically downwards and
   • normal reaction force N directed vertically upwards, exerted by the floor of the lift.
2. As these forces are oppositely directed, the net force in the downward direction will be F = ma – N.
3. Though the weight of a passenger is the gravitational force acting upon it, the person experiences his weight only due to the normal reaction force N exerted by the floor.
4. A lift has zero acceleration when the lift is at rest or is moving upwards or downwards with constant velocity.
5. Thus, a net force acting on the passenger inside the lift will be,
   F = 0 = mg – N
   ∴ mg = N
   Hence, in this case the passenger feels his normal weight mg.

Question 58.
What happens to the apparent weight of the person inside the lift moving with net upward acceleration?
Answer:

1. The lift is said to be moving with net upward acceleration in two possible conditions:
   • when the lift just starts moving upwards or
   • is about to stop at a lower floor during its downward motion.
2. As the net acceleration is upwards, the upward force must be greater.
   ∴ F = ma = N – mg
   ∴ N = mg + ma
   ∴ N > mg
3. Thus, for a passenger inside this lift, his apparent weight is more than his actual weight when the lift was not accelerated.

Question 59.
Why does a passenger feel lighter when the lift is about to stop at a higher floor during its upward motion?
Answer:

1. When the lift is about to stop at a higher floor during its upward motion it has a net downward acceleration.
2. As the net acceleration is downwards, the downward force must be greater.
   ∴ F = ma = mg – N
   ∴ N = mg – ma
   i.e., N < mg
   Hence, a passenger feels lighter when the lift is about to stop at a higher floor during its upward motion.

Question 60.
When does a weighing machine will record zero for a passenger in a lift?
Answer:
If the cables of the lift are cut, the downward acceleration of the lift, a_d = g. In this case, we get,
N = mg – ma_d = 0
Thus, there will not be any feeling of weight and the weighing machine will record zero.

Question 61.
Define time period of a satellite.
Obtain an expression for the period of a satellite in a circular orbit round the Earth. Show that the square of the period of revolution of a satellite is directly proportional to the cube of the orbital radius.
Answer:
Definition:
The time taken by a satellite to complete one revolution around the Earth is called its time period.
Expression for time period:
i) Consider, m = mass of satellite, h = altitude of satellite. Thus, r = R + h = radius of orbit of the satellite.
ii) In one revolution, distance traced by satellite is equal to circumference of its circular orbit.
iii) If T is the time period of satellite, then

Since π², G and M are constant,
∴ T² ∝ r³
Hence, square of the period of revolution of a satellite is directly proportional to the cube of the radius of its orbit.

vi) Taking square roots on both the sides of equation (4), we get,
T = 2π\(\sqrt{\frac{\mathrm{r}^{3}}{\mathrm{GM}}}\)
T = 2π\(\sqrt{\frac{(R+h)^{3}}{G M}}\)
This is the required expression for period of satellite orbiting around the Earth in circular path.

Question 62.
For an orbiting satellite very close to surface of the Earth, show that T = 2π \(\sqrt{\frac{\mathrm{R}}{\mathrm{g}}}\).
Answer:

1. Time period of an orbiting satellite at certain height is given by, T = 2π \(\sqrt{\frac{(R+h)^{3}}{G M}}\)
2. If satellite is orbiting very close to the Earth’s surface, then h ≈ 0
   

Solved Examples

Question 63.
Show that the critical velocity of a body revolving in a circular orbit very close to the surface of a planet of radius R and
mean density ρ is 2R\(\sqrt{\frac{G \pi \rho}{3}}\).
Solution:
Since the body is revolving very close to the surface of a planet,
∴ h << R
R = radius of planet
ρ = mean density of planet
Critical velocity of a body very close to Earth is given by,

Question 64.
Find the orbital speed of the satellite w hen satellite is revolving round the Earth in circular orbit at a distance 9 × 10⁶ m from its centre. (Given: Mass of Earth = 6 × 10²⁴ kg, G = 6.67 × 10^-11 N m²/kg²)
Solution:
Given: r = 9 × 10⁶ m, M = 6 × 10²⁴kg,
G = 6.67 × 10^-11 N m²/kg²
To find: Orbital speed (v_c)
Formula: v_c = \(\sqrt{\frac{\mathrm{GM}}{\mathrm{r}}}\)
Calculation: From formula,

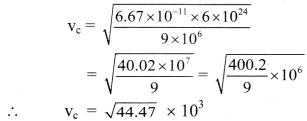
∴ v_c = 6.668 × 10³ m/s
The orbital speed of the satellite is 6.668 × 103 m/s.

Question 65.
Taking radius of the Earth as 6400 km and g at the Earth’s surface as 9.8 m/s², calculate the speed of revolution of a satellite orbiting close to the Earth’s surface.
Solution:
Given: R = 6400 km = 6.4 × 10⁶ m, g = 9.8 m/s²
To find: Critical velocity (v_c)
Formula: v_c = \(\sqrt{\mathrm{gR}}\)
Calculation: From formula,
v_c = \(\sqrt{9.8 \times 6.4 \times 10^{6}}\)
= \(\sqrt{98 \times 64 \times 10^{4}}\)
= 7\(\sqrt{2}\) × 8 ×10²
= 7.92 × 10³ m/s
The speed of revolution of the satellite orbiting close to the Earth’s surface is 7.92 × 10³ m/s.

Question 66.
The critical velocity of a satellite revolving around the Earth is 10 km/s at a height where g_h = 8 m/s ². Calculate the height of the satellite from the surface of the Earth. (R = 6.4 × 10⁶ m)
Solution:
Given: v_c = 10 km/s = 10 × 10³ m/s,
g_h = 8 m/s³, R = 6.4 × 10⁶ m
To find: Height of the satellite (h)
Formula: v_c = \(\sqrt{g_{\mathrm{h}}(R+h)}\)
Calculation: From formula,
10 × 10³ = \(\sqrt{8 \times(\mathrm{R}+\mathrm{h})}\)
Squaring both the sides, we get,
100 × 10⁶ = 8(R + h)
∴ 8(R + h) = 100 × 10⁶
∴ R + h = \(\frac{100}{8}\) × 10⁶
∴ h = 12.5 × 10⁶ – R
= 12.5 × 10⁶ – 6.4 × 10⁶
= 6.1 × 10⁶m
∴ h = 6100 km
The height of the satellite from the surface of the Earth is 6100 km.

Question 67.
An artificial satellite revolves around a planet in circular orbit close to its surface. Obtain the formula for period of the satellite in terms of density p and radius R of planet.
Solution:
Time period of a satellite revolving around the planet at certain height is given by,

Question 68.
Calculate the period of revolution of a polar satellite orbiting close to the surface of the Earth. Given R = 6400 km, g = 9.8 m/s².
Solution:
Given: For satellite close to Earth surface,
R + h ≈ R
R = 6400 km = 6.4 × 10⁶ m, g = 9.8 m/s²
To find: Time period of satellite (T)
Formula: T = 2π \(\sqrt{\frac{R}{g}}\)
Calculation: From Formula,
T = 2 × 3.14 × \(\sqrt{\frac{6.4 \times 10^{6}}{9.8}}\)
= 6.28 × 8.081 × 10²
= 5.075 × 10³ sec
≈ 85 min
The time period of satellite very close to the Earth’s surface is nearly 85 minute.

Question 69.
A satellite orbits around the Earth at a height equal to R of the Earth. Find its period. (R = 6.4 × 10⁶ m, g = 9.8 m/s²)
Solution:
Given: h = R = 6.4 × 10⁶m, g = 9.8 m/s²
To find: Time period (T)

The time period of the satellite is 1.435 × 10⁴ s.

Question 70.
Calculate the height of the communication satellite. (Given: G = 6.67 × 10^-11 N m²/kg², M = 6 × 10²⁴ kg, R = 6400 km)
Solution:
For communication satellite, T = 24 × 60 × 60 s,
Given: M = 6 × 10²⁴ kg,
G = 6.67 × 10^-11 N m²/kg²,
R = 6400 km = 6.4 × 10⁶m
To find: Height (h)

The height of the communication satellite is 35910 km.

Question 71.
How will you ‘weigh the Sun’, that is estimate its mass? The mean orbital radius of the Earth around the Sun is 1.5 × 10⁸ km.
Solution:
Given: r = 1.5 × 10⁸ × 10³m,
T = 365 days = 365 × 24 × 60 × 60 s
To find: Mass (M)
Formula: T = 2π \(\sqrt{\frac{r^{3}}{G M}}\)
Calculation:
From formula,
M = \(\frac{4 \pi^{2} r^{3}}{G T^{2}}\)
= \(\frac{4 \times(3.14)^{2}\left(1.5 \times 10^{11}\right)^{3}}{\left(6.67 \times 10^{-11}\right)(365 \times 24 \times 60 \times 60)^{2}}\)
∴ M = 2.01 × 10³⁰kg
The mass of the Sun is 2.01 × 10³⁰ kg.
[Trick: To ‘weigh the Sun’, i.e., estimate its mass, one needs to know the period of one of its planets and the radius of the planetary orbit.]

Question 72.
Calculate the B.E. of a satellite of mass 2000 kg moving in an orbit very close to the surface of the Earth. (G = 6.67 × 10^-11 N m²/kg²)
Solution:
Given: m = 2 × 10³ kg, R = 6.4 × 10⁶ m,
R = 6.4 × 10⁶ m, M = 6 × 10²⁴kg,
G = 6.67 × 10^-11 N m²/kg²,
M = 6 × 10²⁴ kg
To find: Binding Energy (B.E.)
Formula: For satellite very close to Earth,
B.E. = \(\frac{1}{2} \times \frac{\mathrm{GMm}}{\mathrm{R}}\)
Calculation: From formula,
B.E. = \(\frac{1}{2} \times \frac{6.67 \times 10^{-11} \times 6 \times 10^{24} \times 2 \times 10^{3}}{6.4 \times 10^{6}}\)
∴ B.E. = 6.25 × 10¹⁰ joule
The binding energy of the satellite is 6.25 × 10¹⁰ joule.

Question 73.
Find the binding energy of a body of mass 50 kg at rest on the surface of the Earth. (Given: G = 6.67 × 10^-11 N m²/kg², R = 6400 km, M = 6 × 10²⁴ kg)
Solution:
Given: G = 6.67 × 10^-11 N m²/kg²,
R = 6400 km = 6.4 × 10⁶m,
M = 6 × 10²⁴ kg, m = 50 kg
To find: Binding energy (B.E.)
Formula: B.E. = \(\frac{\text { GMm }}{\mathrm{R}}\)
Calculation: From formula,
B.E. = \(\frac{6.67 \times 10^{-11} \times 6 \times 10^{24} \times 50}{6.4 \times 10^{6}}\)
= \(\frac{2001}{6.4}\) × 10⁷
∴ B.E. = 3.127 × 10⁹ J
The binding energy of the body 3.127 × 10⁹ J.

Question 74.
Find the total energy and binding energy of an artificial satellite of mass 1000 kg orbiting at height of 1600 km above the Earth’s surface.
(Given: G = 6.67 × 10^-11 N m²/kg², R = 6400 km, M = 6 × 10²⁴ kg)
Solution:
Given: h = 1600 km = 1.6 × 10⁶ m,
G = 6.67 × 10^-11 N m²/kg²,
R = 6400 km = 6.4 × 10⁶m,
m = 1000 kg, M = 6 × 10²⁴kg
To find:
i) Total Energy (T.E.)
ii) Binding Energy (B.E.)
Formulae: i. T.E. = –\(\frac{\mathrm{GMm}}{2(\mathrm{R}+\mathrm{h})}\)
ii. B.E. = -T.E.

Calculation: From formula (i),
T.E = – \(\frac{6.67 \times 10^{-11} \times 6 \times 10^{24} \times 1000}{2(6.4+1.6) \times 10^{6}}\)
= –\(\frac{40020 \times 10^{7}}{2 \times 8}\)
∴ T.E. = -2.501 × 10¹⁰J
From formula (ii),
B.E. = 2.501 × 10¹⁰ J
i) The total energy of the artificial satellite is -2.501 × 10¹⁰ J.
ii) The binding energy of the artificial satellite is 2.501 × 10¹⁰ J.

Question 75.
Determine the binding energy of satellite of mass 1000 kg revolving in a circular orbit around the Earth when it is close to the surface of Earth. Hence find kinetic energy and potential energy of the satellite. (Mass of Earth = 6 × 10²⁴ kg, radius of Earth = 6400 km; gravitational constant G = 6.67 × 10^-11 N m²/kg²)
Solution:
Given: m = 1000 kg, M = 6 × 10²⁴ kg,
R = 6400 km, G = 6.67 × 10^-11 N m²/kg²
To find:
i) Binding Energy (B.E.)
ii)Kinetic Energy (K.E.)
iii) Potential Energy (P.E.)

Formulae: For satellite very close to Earth,
i) B.E. = \(\frac{1}{2} \times \frac{\mathrm{GMm}}{\mathrm{R}}\)
ii) K.E.= B.E.
iii) P.E. = -2 K.E.

Calculation: From formula (i),
B.E. = \(\frac{6.67 \times 10^{-11} \times 6 \times 10^{24} \times 1000}{2 \times 6.4 \times 10^{6}}\)
∴ B.E. = 3.1265 × 10¹⁰ J
From formula (ii),
K.E. = 3.1265 × 10¹⁰
∴ K.E. = 3.1265 × 10¹⁰ J
From formula (iii),
P.E. = -2(3.1265 × 10¹⁰)
∴ P.E. = -6.2530 × l0¹⁰J
i) The binding energy of the satellite is 3.1265 × 10¹⁰ J.
ii) The kinetic energy of the satellite is 3.1265 × 10¹⁰ J.
iii) The potential energy of the satellite is -6.2530 × 10¹⁰J.

Apply Your Knowledge

Question 76.
How are Kepler’s law of periods and Newton’s law of gravitation related?
Answer:
Consider a planet of mass m revolving around the Sun of mass M in a circular orbit.
Let,
r = radius of the circular orbit of the planet.
T = Time period of revolution of planet around the Sun.
ω = angular velocity of planet.
F = Centripetal force exerted by the Sun on the planet.
Centripetal force is given by,
F = mrω²;
But ω = \(\frac{2 \pi}{T}\)
∴ F = mr (\(\frac{2 \pi}{\mathrm{T}}\))²
∴ F = \(\frac{4 \pi^{2} \mathrm{mr}}{\mathrm{T}^{2}}\) …(i)
According to Kepler’s third law,
T² ∝ r³
T² = Kr³ ……….. (where, K = constant) (ii)
Substituting equation (ii) in equation (i),
F = \(\frac{4 \pi^{2} \mathrm{mr}}{\mathrm{Kr}^{3}}\)
∴ F = \(\frac{4 \pi^{2}}{\mathrm{~K}} \frac{\mathrm{m}}{\mathrm{r}^{2}}\)
∴ F ∝ \(\frac{\mathrm{m}}{\mathrm{r}^{2}}\) ….(∵ \(\frac{4 \pi^{2}}{\mathrm{~K}}\) is a constant quantity)
Since, the gravitational attraction between the Sun and the planet is mutual, force exerted by the planet on the Sun will be proportional to the mass M of the Sun.
∴ F ∝ \(\frac{\mathrm{Mm}}{\mathrm{r}^{2}}\)
∴ F = \(\frac{\mathrm{GMm}}{\mathrm{r}^{2}}\)
The above equation represents Newton’s law of gravitation. In this manner, Newton’s law of gravitation is derived from Kepler’s law of periods.

Question 77.
Represent graphically the variation of total energy, kinetic energy and potential energy of a satellite with its distance from the centre of the Earth.
Answer:
For a satellite,
Potential energy (U) = \(\)
Kinetic energy (K) = \(\) and
Total energy (E) = \(\), where, r = R + h
Also, U and E remain negative whereas K remains positive.
Hence, the graph will be:

Multiple Choice Questions

Question 1.
Kepler’s law of equal areas is an outcome of
(A) conservation of energy
(B) conservation of linear momentum
(C) conservation of angular momentum
(D) conservation of mass
Answer:
(C) conservation of angular momentum

Question 2.
Amongst given statements, choose the correct statement.
(I) Kepler derived the laws of planetary motion.
(II) Newton provided the reason behind the laws of planetary motion.
(A) (I) is correct.
(B) (II) is correct.
(C) Both (I) and (II) are correct.
(D) Neither (I) nor (II) is correct.
Answer:
(B) (II) is correct.

Question 3.
The figure shows the motion of a planet satellite in terms of mean density of Earth. around the Sun in an elliptical orbit with Sun at the focus. The shaded areas A and B are also shown in the figure which can be assumed to be equal. If t₁ and t₂ represent the time for the planet to move from a to b and d to c respectively, then

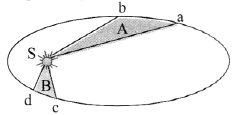
(A) t₁ < t₂
(B) t₁ >t₂
(C) t₁ = t₂
(D) t₁ ≤ t₂
Answer:
(C) t₁ = t₂

Question 4.
A planet is revolving around a star in a circular orbit of radius R with a period T. If the gravitational force between the planet and the star is proportional to R^-3/2, then
(A) T^{2 ∝} R^5/2
(B) T² ∝ R^-7/2
(C) T² ∝ R^3/2
(D) T² ∝ R⁴
Answer:
(A) T² ∝ R^5/2

Question 5.
Time period of revolution of a satellite around a planet of radius R is T. Period of revolution around another planet whose radius is 3R is
(A) T
(B) 9T
(C) 3T
(D) 3\(\sqrt{3}\) T
Answer:
(D) 3\(\sqrt{3}\) T

Question 6.
Newton’s law of gravitation is called universal law because
(A) force is always attractive.
(B) it is applicable to lighter and heavier bodies.
(C) it is applicable at all times,
(D) it is applicable at all places of universe for all distances between all particles.
Answer:
(D) it is applicable at all places of universe for all distances between all particles.

Question 7.
If the mass of a body is M on the surface of the Earth, the mass of the same body on the surface of the moon is
M
(A) 6M
(B) \(\frac{M}{6}\)
(C) M
(D) Zero
Answer:
(C) M

Question 8.
Which of the following statements about the gravitational constant is true?
(A) It has no units.
(B) It has same value in all systems of units.
(C) It is a force.
(D) It does not depend upon the nature of medium in which the bodies lie.
Answer:
(D) It does not depend upon the nature of medium in which the bodies lie.

Question 9.
The gravitational force between two bodies is ______
(A) attractive at large distance only
(B) attractive at small distance only
(C) repulsive at small distance only
(D) attractive at all distances large or small
Answer:
(D) attractive at all distances large or small

Question 10.
Mass of a particle at the centre of the Earth is
(A) infinite.
(B) zero.
(C) same as at other places.
(D) greater than at the poles.
Answer:
(C) same as at other places.

Question 11.
Which of the following is not a property of gravitational force?
(A) It is an attractive force.
(B) It acts along the line joining the two bodies.
(C) The forces exerted by two bodies on each other form an action-reaction pair.
(D) It has a very finite range of action.
Answer:
(D) It has a very finite range of action.

Question 12.
If the distance between Sun and Earth is made two third times of the present value, then gravitational force between them will become
(A) \(\frac{4}{9}\)times
(B) \(\frac{2}{3}\)times
(C) \(\frac{1}{3}\)times
(D) \(\frac{9}{4}\) times
Answer:
(D) \(\frac{9}{4}\) times

Question 13.
The gravitational constant G is equal to 6.67 × 10^-11 N m²/kg² in vacuum. Its value in a dense matter of density 10¹⁰ g/cm³ will be
(A) 6.67 × 10^-1 N m²/kg²
(B) 6.67 × 10^-11 N m²/kg²
(C) 6.67 × 10^-10 N m²/kg²
(D) 6.67 × 10^-21 N m²/kg²
Answer:
(B) 6.67 × 10^-11 N m²/kg²

Question 14.
Acceleration due to gravity above the Earth’s surface at a height equal to the radius of the Earth is ______
(A) 2.5 m/s²
(B) 5 m/s²
(C) 9.8 m/s²
(D) 10 m/s²
Answer:
(A) 2.5 m/s²

Question 15.
If R is the radius of the Earth and g is the acceleration due to gravity on the Earth’s surface, the mean density of the Earth is

Answer:
(D) \(\frac{3 \mathrm{~g}}{4 \pi \mathrm{RG}}\)

Question 16.
Variation of acceleration due to gravity (g) with distance x from the centre of the Earth is best represented by (R → Radius of the Earth)

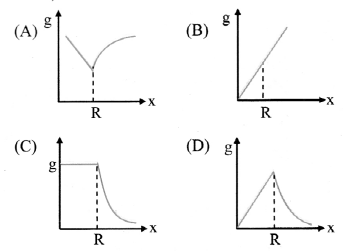
Answer:
(D)

Question 17.
Which of the following statements is not correct for the decrease in the value of acceleration due to gravity?
(A) As we go down from the surtce of the Earth towards its centre.
(B) As we go up from the surface of the Earth.
(C) As we go from equator to the poles on the surface on the Earth.
(D) As the rotational velocity of the Earth is increased.
Answer:
(C) As we go from equator to the poles on the surface on the Earth.

Question 18.
Calculate angular velocity of Earth so that acceleration due to gravity at 60° latitude becomes zero. (Radius of Earth = 6400 km, gravitational acceleration at poles = 10 m/s², cos60° = 0.5)
(A) 7.8 × 10^-2 rad/s
(B) 0.5 × 10^-3 radis
(C) 1 × 10^-3 radis
(D) 2.5 × 10^-3 rad/s
Answer:
(D) 2.5 × 10^-3 rad/s

Question 19.
The gravitational potential energy per unit mass at a point gives ________ at that point.
(A) gravitational field
(B) gravitational potential
(C) gravitational potential energy
(D) gravitational force
Answer:
(B) gravitational potential

Question 20.
A satellite is orbiting around a planet at a constant height in a circular orbit. If the mass of the planet is reduced to half, the satellite would
(A) fall on the planet.
(B) go to an orbit of smaller radius.
(C) go to an orbit of higher radius,
(D) escape from the planet.
Answer:
(D) escape from the planet.

Question 21.
How does the escape velocity of a particle depend on its mass?
(A) m²
(B) m
(C) m⁰
(D) m^-1
Answer:
(C) m⁰

Question 22.
Escape velocity on a planet is ve. If radius of the planet remains same and mass becomes 4 times, the escape velocity becomes
(A) 4v_e
(B) 2v_e
(C) v_e
(D) 0.5 v_e
Answer:
(B) 2v_e

Question 23.
If the escape velocity of a body on Earth is 11.2 km/s, the escape velocity of the body thrown at an angle 45° with the horizontal will be
(A) 11.2 km/s
(B) 22.4 km/s
(C) \(\frac{11.2}{\sqrt{2}}\)km/s
(D) 11.2 \(\sqrt{2}\) km/s
Answer:
(A) 11.2 km/s

Question 24.
Potential energy of a body in the gravitational field of planet is zero. The body must be
(A) at centre of planet.
(B) on the surface of planet.
(C) at infinity.
(D) at distance equal to radius of Earth.
Answer:
(C) at infinity.

Question 25.
If gravitational force of Earth disappears, what will happen to the satellite revolving round the Earth?
(A) Satellite will come back to Earth.
(B) Satellite will continue to revolve.
(C) Satellite will escape in tangential path.
(D) Satellite will start falling towards centre.
Answer:
(C) Satellite will escape in tangential path.

Question 26.
If v_e and v_o represent the escape velocity and orbital velocity of a satellite corresponding to a circular orbit of radius R respectively, then
(A) v_e = v_o
(B) \(\sqrt{2}\)v_o = v_e
(C) v_e = \(\frac{1}{\sqrt{2}}\)v_o
(D) v_e and v_o are not related
Answer:
(B) \(\sqrt{2}\)v_o = v_e

Question 27.
If the kinetic energy of a satellite is 2 × 10⁴ J, then its potential energy will be
(A) – 2 × 10⁴ J
(B) 4 × 10⁴ J
(C) -4 × 10⁴ J
(D) -10⁴J
Answer:
(C) -4 × 10⁴ J

Competitive Corner

Question 1.
A body weighs 200 N on the surface of the Earth. How much will it weigh half way down to the centre of the Earth?
(A) 250 N
(B) 100 N
(C) 150 N
(D) 200 N
Answer:
(B) 100 N
Hint:
Acceleration due to gravity at depth d,
g_d = g (1 – \(\frac{\mathrm{d}}{\mathrm{R}}\))
= g(1 – \(\frac{1}{2}\)) …(∵ d = \(\frac{1}{2}\))
∴ g_d = \(\frac{\mathrm{g}}{2}\)
Weight of the body at depth d = R/2,
W_d = mg_d = m × g/2 = \(\frac{1}{2}\) × 200
∴ W_{d = 100 N}

Question 2.
The work done to raise a mass m from the surface of the Earth to a height h, which is equal to the radius of the Earth, is:
(A) \(\frac{1}{2}\) mgR
(B) \(\frac{3}{2}\) mgR
(C) mgR
(D) 2mgR
Answer:
(A) \(\frac{1}{2}\) mgR
Hint:
Initial potential energy on Earth’s surface,
U_i = \(\frac{-\mathrm{GMm}}{\mathrm{R}}\)
Final potential energy at height h = R
U_f = \(\frac{-\mathrm{GMm}}{2 \mathrm{R}}\)
Work done, W = U_f – U_i

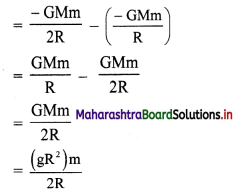
∴ W = \(\frac{1}{2}\) mgR

Question 3.
The time period of a geostationary satellite is 24 h, at a height 6R_E (R_E is radius of Earth) from surface of Earth. The time period of another satellite whose height is 2.5 R_E from surface will be,
(A) \(\frac{12}{2.5}\)h
(B) 6\(\sqrt{2}\) h
(C) 12\(\sqrt{2}\) h
(D) \(\frac{24}{2.5}\)h
Answer:
(B) 6\(\sqrt{2}\) h
Hint:
By Kepler’s third law,

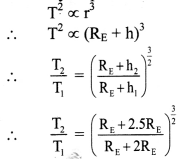
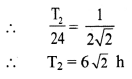
Question 4.
Assuming that the gravitational potential energy of an object at infinity is zero, the change in potential energy (final – initial) of an object of mass m, when taken to a height h from the surface of Earth (of radius R), is given by,
(A) \(\frac{\text { GMm }}{R+h}\)
(B) – \(\frac{\text { GMm }}{R+h}\)
(C) \(\frac{\text { GMmh }}{R(R+h)}\)
(D) mgh
Answer:
(C) \(\frac{\text { GMmh }}{R(R+h)}\)
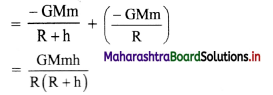
Hint:
Potential energy of object of mass m on the surface of Earth,
P.E = \(\frac{-\mathrm{GMm}}{\mathrm{R}}\)
Potential energy of object of mass m at a height h from the surface of the Earth,
P.E.’ = \(\frac{-\mathrm{GMm}}{\mathrm{R}+\mathrm{h}}\)
∴ Change in potential energy
= P.E.’ – P.E.

Question 5.
A body mass ‘m’ is dropped from height \(\), from Earth’s surface, where ‘R’ is the radius of Earth. Its speed when it will hit the Earth’s surface is (v_e = escape velocity from Earth’s surface)

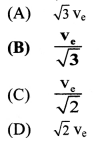
Answer:
(B) \(\frac{\mathbf{v}_{\mathrm{e}}}{\sqrt{3}}\)
Hint:

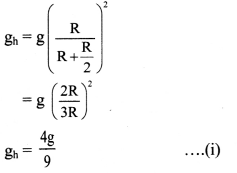
Question 6.
According to Kepler’s Law, the areal velocity of the radius vector drawn from the Sun to any planet always
(A) decreases.
(B) first increases and then decreases.
(C) remains constant.
(D) increases.
Answer:
(C) remains constant.

Question 7.
A body is thrown from the surface of the Earth with velocity ‘u’ m/s. The maximum height in m above the surface of the Earth upto which it will reach is (R = radius of Earth, g = acceleration due to gravity)

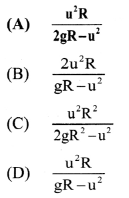
Answer:
(A) \(\frac{u^{2} R}{2 g R-u^{2}}\)
Hint:
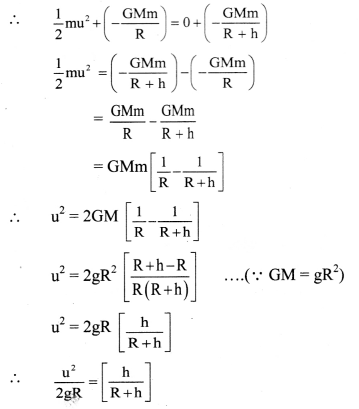
(T.E.) on surface = (T.E.) at height ‘h’
∴ (K.E.)₁ + (P.E.)₁ = (K.E.)₂ + (P.E.)₂

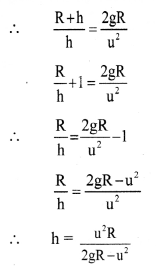
Question 8.
A satellite is revolving in a circular orbit at a height ‘h’ above the surface of the Earth of radius ‘R’. The speed of the satellite in its orbit is one-fourth the escape velocity from the surface of the Earth. The relation between ‘h’ and ‘R’ is
(A) h = 2R
(B) h = 3R
(C) h = 5R
(D) h = 7R
Answer:
(D) h = 7R
Hint:

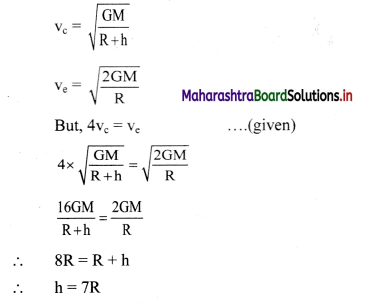
Question 9.
Two astronauts are floating in gravitational free space after having lost contact with their spaceship. The two will:
(A) keep floating at the same distance between them.
(B) move towards each other.
(C) move away from each other.
(D) will become stationary.
Answer:
(B) move towards each other.