Maharashtra Board Class 11 Chemistry Important Questions Chapter 13 Nuclear Chemistry and Radioactivity

Balbharti Maharashtra State Board 11th Chemistry Important Questions Chapter 13 Nuclear Chemistry and Radioactivity Important Questions and Answers.

Maharashtra State Board 11th Chemistry Important Questions Chapter 13 Nuclear Chemistry and Radioactivity

Question 1.
Explain the term nuclear chemistry. Give a few examples of nuclear reactions.
Answer:
Nuclear chemistry is a branch of physical chemistry and it deals with the study of reactions involving changes in atomic nuclei. This branch started with the discovery of natural radioactivity by physicist Antoine Henri Becquerel.

Examples of nuclear reactions are as follows:

• Radioactive decay
• Artificial transmutation
• Nuclear fission
• Nuclear fusion

Question 2.
Write a short note on similarity between the solar system and structure of atom.
Answer:
Solar system: It consists of the Sun and planets in which Sun is at the centre of solar system and planets move around it under the force of gravity.

Atomic system: It consists of tiny central core called as nucleus at the centre of atom around which electrons are present. Like in solar system, electrostatic attractions hold subatomic particles in a structure of atom. The nucleus consists of protons and neutrons.

Question 3.
Answer the following.
i. Give the symbolic representation for calcium, (no. of protons = 20, mass number = 40)
ii. Calculate the number of neutrons for calcium.
Answer:
i. \({ }_{20}^{40} \mathrm{Ca}\), in which Z = 20 and A = 40.
ii. Number of neutrons: It can be calculated from formula (A = Z + N).
For calcium, N = A – Z = 40 – 20 = 20
Nucleus of the calcium atom contains 20 neutrons.

Question 4.
Explain the term nucleons with examples.
Answer:
The term nucleon refers to the sum of protons (p) and neutrons (n) present in atom, e.g. Number of nucleons present in \({ }_{20}^{40} \mathrm{Ca}\) are 40 (i.e., 20 protons and 20 neutrons). Number of nucleons present in \({ }_{11}^{23} \mathrm{Na}\) are 23 (i.e., 11 protons and 12 neutrons).

Question 5.
Define: Nuclide
Answer:
The nucleus of a specific isotope is called as nuclide.

Question 6.
Atom as a whole is electrically neutral. Justify.
Answer:

• The magnitude of electronic charge (e) on the nucleus is +Ze and that of outer sphere is -Ze. Number of protons and number of electrons are always equal in an atom.
• As a result of this, the charges get nullified, therefore, the atom as a whole is electrically neutral.

Question 7.
Define:
i. Isotopes
ii. Isobars
Answer:
i. Isotopes: Nuclides which contain same number of protons but different number of neutrons in their nuclei are called as isotopes. e.g. \({ }_{11}^{22} \mathrm{Na}\), \({ }_{11}^{23} \mathrm{Na}\) and \({ }_{11}^{24} \mathrm{Na}\)
ii. Isobars: Nuclides (of different element) which have same mass number but have different number of protons and neutrons in their nuclei are called as isobars.
OR
The atoms of different elements having the same mass number but different atomic numbers are called isobars.
e.g. \({ }_{6}^{14} \mathrm{C}\) and \({ }_{7}^{14} \mathrm{N}\)

Question 8.
Define mirror nuclei and isotones.
Answer:

• Isobars in which the number of protons and neutrons differ by 1 unit and are interchanged are called as mirror nuclei.
• Isotones are defined as nuclides having the same number of neutrons but different number of protons and hence, different mass numbers.

Question 9.
Name the following.
i. Nuclides in which number of protons and neutrons differ by 1 and are interchanged.
ii. Nuclides having the same number of neutrons but different number of protons.
iii. Nuclides with the same mass number which differ in energy states.
Answer:
i. Mirror nuclei
ii. Isotones
iii. Nuclear isomers

Question 10.
Explain the term nuclear isomers?
Answer:

• The nuclides with the same number of protons (Z) and neutrons (N) or the same mass number (A) which differ in energy states are called nuclear isomers.
• In this, the isomer of higher energy is said to be in the metastable state which is represented by writing “m” after the mass number.
  e.g. Nuclear isomers of cobalt can be represented as, ^60mCo and ⁶⁰Co.

Question 11.
State true or false. Correct the false statement.
i. The number of nucleons in C-12 atom is 6.
ii. N-13 and C-13 are mirror nuclei.
iii. Nuclear isomers have same number of protons and neutrons.
Answer:
i. False,
The number of nucleons in C-12 atom is 12.
ii. True
iii. True

Question 12.
Give classification of nuclides on the basis of nuclear stability.
Answer:
Nuclides can be classified into stable and unstable/radioactive nuclides on the basis of nuclear stability.

• Stable nuclides: In this type of nuclides, the number of electrons and the location of nuclei may change in outer sphere but the number of protons and neutrons remain unchanged.
• Radioactive (unstable) nuclides: These nuclides undergo spontaneous change forming new nuclides.

Question 13.

	Number of protons (Z)	Number of neutrons (N)	Number of such nuclides
i.	Even	Even	165
ii.	Even	Odd	55

What conclusion can be drawn from the above given data?
Answer:

• Number of nuclides with even ‘Z’ and even ‘N’ are higher in number as compared to nuclides with even ‘Z’ and odd ‘N’
• Nuclides with even number of ‘Z’ and odd number of ‘N’ are about 1/3rd of nuclides where both ‘Z’ and ‘N’ are even.
• Nuclides with even number of protons (Z) and even number of neutrons (N) are most stable. These nuclides tend to fonn proton-proton and neutron-neutron pairs. This impart stability to the nucleus.

Question 14.
Write a note on naturally occurring nuclides with either odd number of protons or odd number of neutrons.
Answer:
i. The number of stable nuclides with either Z or N odd is about one third of nuclides where both are even.
ii. These nuclides are less stable than those having even number of protons and neutrons.
iii. In these nuclides one nucleon has no partner and therefore, these nuclides are less stable.
iv. Further the number of nuclides with odd A are nearly the same, irrespective of Z or N is odd. This indicates that protons and neutrons behave similarly in the respect of stability.
v. Following table gives the estimate of such nuclides occurring in nature.

	Number of protons (Z)	Number of neutrons (N)	Number of such nuclides
i.	Even	Odd	55
ii.	Odd	Even	50

Question 15.
State true or false. Correct the false statements.
i. The nuclides with even Z and even N constitute 85% of earth crust.
ii. Nuclides with either ‘Z’ or ‘N’ odd are more stable than those having even number of both ‘Z’ and ‘N’
iii. The number of nuclides with odd number of ‘Z’ and odd number of ‘N’ are only four.
Answer:
i. True
ii. False
Nuclides with either ‘Z’ or ‘N’ odd are less stable than nuclides having even number of both ‘Z’ and ‘N’.
iii. True

Question 16.
Heavier nuclides require greater number of neutrons (than protons) to attain stability. Justify.
Answer:

• The heavier nuclides with the increasing number of protons lead to large coulombic repulsions.
• Increased number of neutrons will separate the protons within the nuclei, which will impart stability. Thus, in order to attain stability heavier nuclide need more number of neutrons.

Question 17.
Consider the graph of neutron (N) plotted against proton number (Z). How will you identify radioactive nuclides from the graph?
Answer:
Nuclides which fall outside the belt or stability zone are radioactive nuclides.

Question 18.
Write a note Magic numbers.
Answer:
Magic numbers: The nuclei with 2, 8, 20, 28, 50, 82 and 126 neutrons or protons are particularly stable and abundant in nature. These numbers are known as magic numbers.
e.g. Lead (\({ }_{82}^{208} \mathrm{~Pb}\)) has two magic numbers, 82 protons and 126 neutrons.

Question 19.
What is the order of distance between two protons present in the nucleus?
Answer:
The order of distance between two protons present in the nucleus is typically of order of 10^-15 m.

Question 20.
Which factor is responsible for nuclear stability?
Answer:
Nuclear forces of attractions exist within nuclei. These are attractions between proton-proton (p-p), neutron-neutron(n-n) and proton-neutron(p-n). They constitute or give rise to nuclear potential which is responsible for nuclear stability.

Question 21.
Write short notes on: nuclear potential.
Answer:

• Nuclear potential is the attraction between p-p, n-n and p-n.
• These attractive forces are independent of the charge on nucleons or attraction between p-p, n-n and p-n are equal.
• These attractive forces operate over short range within the nucleus.
• Nuclear potential is responsible for the nuclear stability.

Question 22.
State true or false. Correct the false statement.
i. The nuclear forces of attractions are dependent on the charge on the nucleons.
ii. The actual mass of an atom is observed to be more than sum of the masses of its constituents.
Answer:
i. False
The nuclear forces of attractions are independent of the charge on the nucleons.
ii. False
The actual mass of an atom is observed to be less than sum of the masses of its constituents.

Question 23.
Define: Nuclear binding energy
Answer:
An energy equivalent to the mass lost is released during the formation of nucleus. This is called the nuclear binding energy.
OR
The energy requiredfor holding the nucleons together within the nucleus of an atom is called as the nuclear binding energy.

Question 24.
Explain the term: mass defect.
Answer:
During the formation of nucleus, certain mass is lost. This phenomenon is known as mass defect (Δm).
The exact mass of nucleus is slightly less than sum of the exact masses of the constituent nucleons. This difference is called as mass defect. It is represented by symbol Δm.
Formulae: Δm = calculated mass – observed mass

Question 25.
Explain the relation between nuclear mass and energy? Also give the energy released in the conversion of one atomic mass unit into energy.
Answer:
i. The nuclear mass is expressed in atomic mass unit (u) which is exactly 1/12^th of the mass of ¹²C atom. Thus, u = 1/12^th mass of C-12 atom = 1.66 × 10^-2 kg.
ii. The conversion of mass into energy is established through Einstein’s equation, E = mc².
Where m is the mass of matter converted into energy (E) and velocity of light (c).
iii. The energy released in the conversion of one u mass into energy is given by:
E = mc² = (1.66 × 10^-27kg) × (3 × 10⁸ m s^-1)²

Question 26.
Derive the expression for nuclear binding energy for a nuclide.
Answer:
Expression for nuclear binding energy:
i. Consider a nuclide \({ }_{z}^{A} X\) that contains Z protons and (A – Z) neutrons. Suppose the mass of the nuclide is m. The mass of proton is m_p and that of neutron is mn.

ii. Total mass = (A – Z)m_n + Zm_p + Zm_e …..(1)
Δm = [(A – Z)m_n + Zm_p + Zm_e] – m
= [(A – Z)m_n + Z(m_p + m_e] – m
= [(A – Z)m_n + Zm_H] – m …..(2)
Where (m_p + m_e) = m_H = mass of H atom.
Thus, (Δm) = [Zm_p + (A – Z)m_n] – m
Where Z = atomic number
A = mass number
(A – Z) = neutron number
m_p and m_n = masses of proton and neutron, respectively
m = mass of nuclide

iii. The mass defect, Δm is related to binding energy of nucleus by Einstein’s equation,
ΔE = Δm × c²
Where, ΔE = Binding energy, Δm = mass defect.
iv. Nuclear energy is measured in million electro volt (MeV).
v. The total binding energy is then given by,
B.E. = Δm (u) × 931.4
Where 1.00 u = 931.4 MeV
B.E. = 931.4 [Zm_H + (A – Z)m_n – m] ……(3)
Total binding energy of nucleus containing A nucleons is the B.E.
vi. The binding energy per nucleon is then given by,
\(\bar{B}\) = B.E./A

Question 27.
Calculate the mean binding energy per nucleon for the formation of \({ }_{8}^{16} \mathrm{O}\) nucleus. The mass of oxygen atom is 15.994 u. The masses of H atom and neutron are 1.0078 u and 1.0087 u, respectively.
Solution:
Given: m_H = 1.0078 u
m_n= 1.0087 u
m= 15.994 u
Z = 8, A= 16
To find: Mean binding energy per nucleon (\(\bar{B}\))
Formulae: i. Δm = Zm_H + (A – Z)m_n – m
ii. B.E. = Δm × 931.4 MeV
iii. \(\overline{\mathrm{B}}=\frac{\mathrm{B} . \mathrm{E} .}{\mathrm{A}}\)
Calculation: i. The mass defect, Δm = Zm_H + (A – Z)m_n – m
Δm = 8 × 1.0078 u + 8 × 1.0087 u – 15.994 u = 0.138 u
ii. Total binding energy, B.E. (MeV) = Δm (amu) × 931.4
Hence, B.E. = 0.138 × 931.4 = 128.533 MeV
iii. Binding energy per nucleon, \(\overline{\mathrm{B}}=\frac{\mathrm{B} . \mathrm{E} .}{\mathrm{A}}\)
Hence, \(\bar{B}\) = \(\frac{128.533}{16}\) = 8.033 MeV/nucleon
Ans: Binding energy per nucleon for the formation of \({ }_{8}^{16} \mathrm{O}\) nucleus = 8.033 MeV/nucleon

Question 28.
Calculate the binding energy per nucleon for the formation of \({ }_{2}^{4} \mathrm{He}\) nucleus. Mass of \({ }_{2}^{4} \mathrm{He}\) atom = 4.0026 u.
Solution:
Given: m = 4.0026 u
Z = 2, A = 4
To find: Binding energy per nucleon (\(\bar{B}\))
Formulae: i. Δm = Zm_H + (A – Z)m_n – m
ii. B.E. = Δm × 931.4 MeV
iii. \(\overline{\mathrm{B}}=\frac{\mathrm{B} . \mathrm{E} .}{\mathrm{A}}\)
The mass defect, Δm = [Zm_H + (A – Z)m_n] – m
Δm = [(2 × 1.0078) + (2 × 1.0087)] – 4.0026 = 0.0304 u
Total binding energy, B.E. (MeV) = Δm (amu) × 931.4
= 0.0304 × 931.4
= 28.315 MeV
iii. B.E. per nucleon, \(\overline{\mathrm{B}}=\frac{\mathrm{B} . \mathrm{E} .}{\mathrm{A}}\)
\(\bar{B}\) = \(\frac{28.315}{4}\) = 7.079 Mey/nucleon
Ans: Binding energy per nucleon for formation of \({ }_{2}^{4} \mathrm{He}\) nucleus = 7.079 MeV/nucleon

Question 29.
Define radioactivity and give examples of two radioactive elements.
Answer:
Radioactivity is a phenomenon in which the nuclei spontaneously emit a nuclear particle and gamma radiation transforming to a different nuclide. e.g. Uranium and radium
[Note: Radioactivity is the phenomenon related to the nucleus.]

Question 30.
What is the criteria for an element to be known as radioactive element?
Answer:

• An element is considered to be radioactive if the nuclei of its atoms are unstable.
• That is, when element undergoes nuclear changes (i.e., emission of nuclear particles and gamma radiation), it is said to be radioactive.

Question 31.
What are the different types of radiations emitted by radioactive element?
Answer:
The radiations emitted by radioactive elements are as follows:

• Alpha (α) radiations
• Beta (β) radiations
• Gamma (γ) radiations

Question 32.
Write the unit of rate of decay.
Answer:
The rate of decay is expressed in the form of disintegrations per second (dps).

Question 33.
Derive the equation λ = \(\frac{\left(-\frac{\mathbf{d} \mathbf{N}}{\mathbf{d} \mathbf{t}}\right)}{\mathbf{N}}\) and write what does λ denotes.
Answer:
The rate of decay of a radioelement at any instant is proportional to the number of nuclei (atoms) present at that instant. It can be represented as,
\(-\frac{\mathrm{d} \mathrm{N}}{\mathrm{dt}} \propto \mathrm{N} \quad \text { or }-\frac{\mathrm{d} \mathrm{N}}{\mathrm{dt}}=\lambda \mathrm{N}\) …….(i)
Where, \(-\frac{\mathrm{d} \mathrm{N}}{\mathrm{dt}}\) = Rate of decay at any time, t
λ = Decay constant
N = Number of nuclei (atoms) present at time, t
From equation (i),

Decay constant (λ) is the fraction of nuclei decaying in unit time.
OR
It is the ratio of the amount of substance disintegrated per unit time to the amount of substance present at that time.

Question 34.
Derive the expression for decay constant.
Answer:
Decay constant (λ) is the fraction of nuclei decaying in unit time.
Thus,
λ = \(-\frac{d N}{d t} \times \frac{1}{N}\) …(i)
Rearranging equation (i) we get,
\(\frac{\mathrm{d} \mathrm{N}}{\mathrm{N}}\) = -λ dt
On integrating above equation, we get
∫\(\frac{\mathrm{d} \mathrm{N}}{\mathrm{N}}\) = -∫ λ dt …(ii)
On performing the integration, we get lnN = -λt + C ……(iii)
where C is the constant of integration whose value is obtained as follows:
Let N₀ be the number of nuclei present at some arbitrary zero time. At time t, the number of nuclei is N. So, at t = 0, N = N₀, substituting in equation (iii), we get
lnN₀ = C
With this value of C, equation (iii) becomes
lnN = -λt + lnN₀
or λt = lnN₀ – InN = ln \(\frac{\mathrm{N}_{0}}{\mathrm{~N}}\) ……(iv)
Hence, λ = \(\frac{1}{t} \ln \frac{N_{0}}{N}\) …….(v)
Converting natural logarithm (ln) to logarithm to the base 10, equation (v) becomes
λ = \(\frac{2.303}{t} \log _{10} \frac{N_{0}}{N}\) ………(vi)
The equation (iv) can be expressed as ln \(\frac{\mathrm{N}_{0}}{\mathrm{~N}}\) = -λt. Taking antilog of both sides, we get
\(\frac{\mathrm{N}}{\mathrm{N}_{0}}=\mathrm{e}^{-\lambda \mathrm{t}} \text { or } \mathrm{N}=\mathrm{N}_{0} \mathrm{e}^{-\lambda t}\) …….(vii)
The equation (vi) and equation (vii) give the decay constant.

Question 35.
Write a note on half-life of a radioelement.
Answer:

• Half-life of a radioelement (t_1/2): It is the time needed for a given number of nuclei (atoms) of radioelement to decay exactly to half of its initial value.
• Each radio isotope has its own half-life.
• Half-life of a radioelement can be expressed in seconds, minutes, hours, days or years.
• Mathematical expression for half-life of a radioelement can be given as,
  \(t_{1 / 2}=\frac{0.693}{\lambda}\)

Question 36.
Complete the following statements based on the given graph.
i. As decay progresses, the number of radioactive atoms will ……….. with time.
ii. As decay progresses, the rate of decay will …………..
iii. Rate of radioactive decay at any instant is ………… to the number of atoms of the radioactive element present at that instant.
Answer:
i. decrease
ii. decrease
iii. proportional

Question 37.
²¹⁸Po decays initially at a rate of 816 dps. The rate falls to 408 dps after 24 min. Calculate the decay constant.
Solution:

Question 38.
After how many seconds will the concentration of radioactive element X will be halved, if the decay constant is 1.155 × 10^-3 s^-1?
Solution:

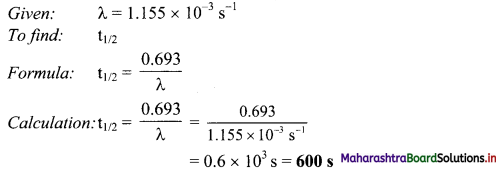
Ans: Concentration of radioactive element (X) will be halved in 600 s.

Question 39.
⁴¹Ar decays initially at a rate of 575 Bq. The rate falls to 358 dps after 75 minutes. What is the half-life of ⁴¹Ar?
Solution:


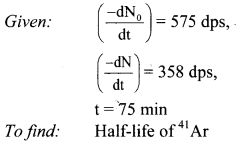
Ans: The half-life of Ar is 109.7 min.

Question 40.
The half-life of ³²P is 14.26 d. What percentage of ³²P sample will remain after 40 d?
Solution:
Given: t_1/2 = 14.26 d,
N₀ = 100,
t = 40 d
To find: Percentage of ³²P sample remaining after 40 d

Question 41.
The half-life of ³⁴Cl is 1.53 s. How long does it take for 99.9 % of sample of ³⁴Cl to decay?
Solution:
Given: t_1/2 = = 1.53 s,
N₀ = 100,
N = 100 – 99.9 = 0.1,
To find: Time (t)

Question 42.
The half-life of ²⁰⁹Po is 102 y. How much of 1 mg sample of polonium decays in 62 y?
Solution:
Given: t_1/2 = 102y,
t = 62 y,
N₀ = 1 mg
To find: Amount of polonium that decayed in 62 y

Taking antilog of both sides we get,
\(\frac{\mathrm{N}_{0}}{\mathrm{~N}}\) = antilog (0.1829) = 1.524
N = \(\frac{\mathrm{N}_{0}}{1.524}=\frac{1 \mathrm{mg}}{1.524}\) = 0.656 mg
N is the amount that remains after 62 y.
Hence, the amount decayed in 62 y = 1 mg – 0.656 mg = 0.344 mg
Ans: The amount decayed in 62 y is 0.344 mg

Question 43.
What will be the approximate time taken for 90 % decay of ¹⁷⁴Ir in terms of its half-life?
Solution:
Given: N₀ = 100
N = 100 – 90 = 10
To find: Time (t)

Ans: Thus, the approximate time required for 90 % decay of ¹⁷⁴Ir in terms of its half-life is 3.3t_1/2.

Question 44.
A radioactive decay of element X (Z = 35) is 30 % complete in 2 hours. Calculate its half-life period.
Solution:
Given: t = 2 hrs,
N₀ = 100
N= 100 – 30 = 70
To find: t_1/2

Question 45.
What are the different modes by which radio elements decay?
Answer:
There are 3 modes by which radio elements decay: α-decay, β-decay and γ-emission.

Question 46.
What is α-decay?
Answer:
Radioactive isotope/radioelement when undergoes decay by the emission of α-particle from the nuclei then the process involved is referred to as α-decay.

Question 47.
Give equation for radium-222 when it undergoes decay by emission of an α-particle.
\({ }_{88}^{226} \mathrm{Ra} \longrightarrow{ }_{86}^{222} \mathrm{X}+{ }_{2}^{4} \mathrm{He}\)
Answer:
\({ }_{88}^{226} \mathrm{Ra} \longrightarrow{ }_{86}^{222} \mathrm{X}+{ }_{2}^{4} \mathrm{He}\)
Thus, atomic number of element ‘X’ will be 86 and atomic mass number will be 222.

Question 48.
Identify the mode of decay and state whether following equation is CORRECT or NOT. Justify.
\({ }_{92}^{238} \mathbf{U} \longrightarrow{ }_{90}^{234} \mathrm{Th}+{ }_{2}^{4} \mathbf{H e}\)
Ans:
i. It involves α-decay process.
ii. As uranium undergoes decay by emission of an α-particle (i.e., \({ }_{2}^{4} \mathrm{He}\)), daughter nuclei (in this case thorium) ‘will observe the decrease in atomic number by 2 units and decrease in atomic mass number by 4 units.
Hence, the given equation is correct.

Question 49.
If radioactive element ‘X’ undergoes α-emission then what will be the position of daughter nuclei in the periodic table with respect to element ‘X’.
Answer:
If radioactive element ‘X’ undergoes α-emission, then corresponding daughter nuclei formed will occupy two places to the left of the periodic table with respect to element ‘X’.

Question 50.
What is β^– – decay? Also explain the changes that occur in the parent nuclei due to β-emission with one example.
Answer:
β^– – decay: The emission of negatively charged stream of β^– particles from the nucleus is called β^– – decay.
i. β^– – Particles are electrons with a charge and mass of an electron, mass being negligible as compared to the nuclei.
ii. When a nucleus decays by emitting a high-speed electron called a beta particle (β), a new nucleus is formed with the same mass number as the original nucleus and with an atomic number that is one unit greater than the parent nuclei.
General equation:

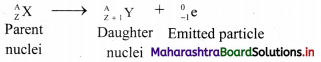
Note: The mass number A does not change, the atomic number changes when a nuclei undergoes β-decay. e.g. Neptunium-238 decays to form plutonium-238:

Question 51.
Mention the atomic number and atomic mass number of the parent radioelement ‘X’ in the following case if parent nuclei undergo β-emission.
i. \(\mathrm{X} \longrightarrow{ }_{94}^{238} \mathrm{Pu}\)
ii. \(\mathrm{X} \longrightarrow{ }_{95}^{241} \mathrm{Am}\)
Answer:

Question 52.
How many α and β-particles are emitted in the following?
\({ }_{93}^{237} \mathrm{~Np} \longrightarrow{ }_{83}^{209} \mathrm{Bi}\)
Answer:
The emission of one α-particle decreases the mass number by 4 whereas the emission of β particles has no effect on mass number.
Net decrease in mass number = 237 – 209 = 28. This decrease is only due to α- particles. Hence, number of α- particles emitted = \(\frac {28}{4}\) = 7
Now, the emission of one α-particle decreases the atomic number by 2 and one β-particle emission increases it by 1.
The net decrease in atomic number = 93 – 83 = 10
The emission of 7 α-particles causes decrease in atomic number by 14. However, the actual decrease is only 10. It means atomic number increases by 4. This increase is due to emission of 4 β-particles.
Thus, 7 α and 4 β- particles are emitted.

Question 53.
Explain the process of γ-decay in detail with a suitable example.
Answer:
γ-decay:
i. γ-Radiation is always accompanied with α and β^– decay processes.
ii. During γ-radiation, the daughter nucleus is left in energetically excited state which decays to the ground state of product with emission of γ-rays.
For example, \({ }_{92}^{238} \mathrm{U} \longrightarrow{ }_{90}^{234} \mathrm{Th}+{ }_{2}^{4} \mathrm{He}+\gamma\)
iii. \({ }_{92}^{238} \mathrm{U}\) emits α-particles of two different energies, 4.147 MeV (23%) and 4.195 MeV (77%).
iv. When α-particles of energy 4.147 MeV are emitted, ²³⁴Th is left in an excited state which de-excites to the ground state with emission of γ-ray photons with energy 0.0048 MeV.

Question 54.
Half-life of ²⁰⁹Po is 102 y. How many α-particles are emitted in 1 s from 2 mg sample of Po?
Solution:
Given: t_1/2 = 102 y,
t = 1 s,
Amount of sample = 2 mg
To find: Number of α-particles emitted

Question 55.
Nuclear transmutation is a spontaneous or non-spontaneous process?
Answer:
Nuclear transmutation is a non-spontaneous (man-made) process.

Question 56.
What is nuclear transmutation?
Answer:
Nuclear transmutation:

• It is the process of transformation of a stable nucleus into another nucleus which can be stable or unstable.
• It can occur by the radioactive decay of a nucleus or the reaction of a nucleus with another particle.

Question 57.
Differentiate between chemical reactions and nuclear reactions.
Answer:
Chemical reactions:

• Rearrangement of atoms by breaking and forming of chemical bonds.
• Different isotopes of an element have same behaviour.
• Only outer shell electrons take part in the chemical reaction.
• The chemical reaction is accompanied by relatively small amounts of energy.
  e.g. chemical combustion of 1.0 g methane releases only 56 kJ energy.
• The rates of reaction are influenced by the temperature, pressure, concentration and catalyst.

Nuclear reactions:

• Elements or isotopes of one element are converted into another element in a nuclear reaction.
• Isotopes of an element behave differently.
• In addition to electrons, protons, neutrons, other elementary particles may be involved.
• The nuclear reaction is accompanied by a large amount of energy change, e.g. The nuclear transformation of 1 g of Uranium – 235 release 8.2 × 10⁷ kJ
• The rate of nuclear reactions is unaffected by temperature, pressure and catalyst.

Question 58.
What will happen when a nucleus of J’B is bombarded with α-particle? Identify the process involved.
Answer:
i. When a stable nucleus of \({ }_{5}^{10} \mathrm{~B}\) is is bombarded with α-particle, it transforms into \({ }_{7}^{13} \mathrm{~N}\), which is radioactive and spontaneously emits positrons to produces \({ }_{6}^{13} \mathrm{C}\).
This can be represented as,

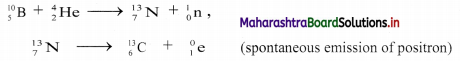
ii. The process involved is known as induced radioactivity or artificial radioactivity.

Question 59.
Define: Nuclear fission
Answer:
Nuclear fission is defined as a process which involves splitting of the heavy nucleus of an atom into two nearly equal fragments accompanied by release of the large amount of energy.

Question 60.
Nuclear fission of ²³⁵U is a chain process. Justify.
Answer:

• Nuclear fission of ²³⁵U occurs when nucleus absorbs neutron. When a uranium nucleus absorbs neutron, it breaks into two lighter fragments and releases energy (heat), more neutrons, and other radiation.
• When one uranium 235 nucleus undergoes fission, three neutrons are emitted.
• These neutrons emitted in fission cause more fission of the uranium nuclei which yield more neutrons. These neutrons again bring forth fission producing further neutrons.
• The process continues indefinitely leading to chain reaction which continues even after the removal of bombarding neutrons.

Question 61.
Explain the term: Nuclear fusion and give one example.
Answer:
Nuclear fusion: In this process, the lighter nuclei combine (fuse) together and form a heavy nucleus which is accompanied by an enormous amount of energy.
e. g. The energy received by earth from the sun is due to the nuclear fusion reactions.

Question 62.
Which will produce more energy: Nuclear fission or fusion?
Answer:
Nuclear fusion will produce relatively more energy per given mass of fuel.

Question 63.
What is the range of temperature required to carry out nuclear fusion reaction?
Answer:
Nuclear fusion reaction requires extremely high temperature typically of the order of 108 K.

Question 64.
Distinguish between nuclear fission and nuclear fusion.
Answer:
Nuclear fission:

• It is the process in which a heavy nucleus splits up into two lighter nuclei of nearly equal masses.
• About 200 MeV of energy is available per fission in case of \({ }_{92}^{235} \mathrm{U}\).
• The products of nuclear fission are, in general, radioactive.

Nuclear fusion:

• It is the process in which two lighter nuclei combine together to form a heavy nucleus.
• Energy available per fusion is much less but the energy per unit mass of material is much greater than that for fission of heavy nuclei.
• The products of fusion are, in general, non-radioactive.

Question 65.
Estimate the energy released in the fusion reaction.
\({ }_{1}^{2} \mathbf{H}+{ }_{2}^{3} \mathbf{H e} \longrightarrow{ }_{2}^{4} \mathbf{H e}+{ }_{1}^{1} \mathbf{H}\)
(Given atomic masses: ²H = 2.0141 u. ³He = 3.0160 u, ⁴He = 4.0026 u, ¹H = 1.0078 u)
Answer:

Question 66.
Explain the term: Radiocarbon dating in detail.
Answer:
Radiocarbon dating: The technique is used to find the age of historic and archaeological organic samples such as old wood samples and animal or human fossils.
Radioisotope used for carbon dating is ¹⁴C.
i. Radioactive ¹⁴C is formed in the upper atmosphere by bombardment of neutrons from cosmic ray on ¹⁴N.
\({ }_{7}^{14} \mathrm{~N}+{ }_{0}^{1} \mathrm{n} \longrightarrow{ }_{6}^{14} \mathrm{C}+{ }_{1}^{1} \mathrm{H}\)
ii. ¹⁴C combines with atmospheric oxygen to form ¹⁴CO₂ which mixes with ordinary ¹²CO₂.
iii. This carbon dioxide is absorbed by plants during photosynthesis.
iv. Animals eat plants which have absorbed a carbon dioxide (¹⁴CO₂ + ¹²CO₂). Hence, ¹⁴C becomes a part of plant and animal bodies.
v. As long as the plant is alive, the ratio ¹⁴C/¹²C remains constant.
vi. When the plant dies, photosynthesis will not occur and the ratio ¹⁴C/¹²C decreases with the decay of radioactive ¹⁴C which has a half-life 5730 years.
vii. The decay process of ¹⁴C is given below:
\({ }_{6}^{14} \mathrm{C} \longrightarrow{ }_{7}^{14} \mathrm{~N}+{ }_{-1}^{0} \mathrm{e}\)
viii. The activity (N) of given wood sample and that of fresh sample of live plant (N0) is measured, where, N0 denotes the activity of the given sample at the time of death.
ix. The age of the given wood sample, can be determined by applying following Formulae:

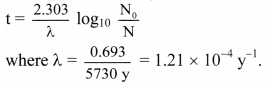
Question 67.
What is nuclear power?
Answer:
Nuclear power is the electricity generated from the fission of uranium and plutonium.

Question 68.
Nuclear power is a clean source of energy. Justify.
Answer:
Nuclear power offers huge environmental benefits in producing electricity because,

• it releases zero carbon dioxide.
• it releases zero sulphur and nitrogen oxides.
• these are atmospheric pollutants which pollute the air.

Thus, nuclear power is a clean source of energy.

Question 69.
How much energy will be produced by fission of 1 gram of ²³⁵U?
Answer:
Fission of 1 gram of uranium-235 produces about 24,000 kW/h of energy.

Question 70.
Nuclear fission is an alternative energy source. Explain.
Answer:

• Fission of 1 gram of uranium-235 produces about 24,000 kW/h of energy.
• This is the same amount of energy produced by burning 3 tons of coal or 12 barrels of oil, or nearly 5000 m³ of natural gas.
• The sources like coal, oil, natural gas are depleting very fast.
• Also, the costs of petrol and other products from petroleum industry is increasing.
• Thus, we need to depend on the nuclear fission as an alternative source of energy for electricity.

Question 71.
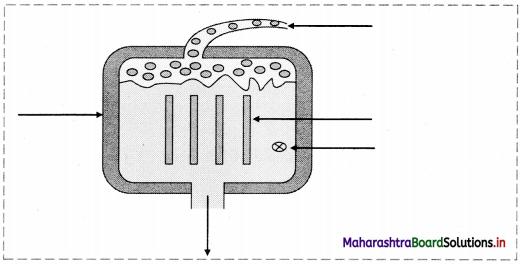
Label the follow ing diagram of simplified nuclear reactor.

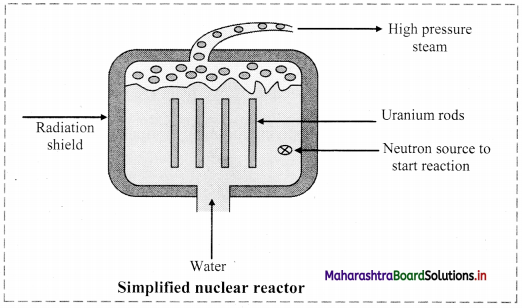
Answer:

Question 72.
Explain in brief: Nuclear reactor
Answer:
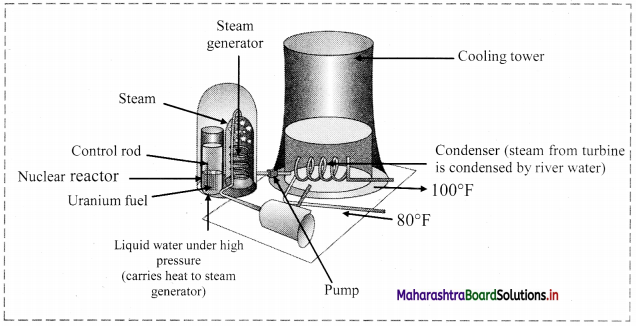
Nuclear reactor: Nuclear reactor is a device for using atomic energy in controlled manner for peaceful purposes. During nuclear fission energy is released. The released energy can be utilized to generate electricity in a nuclear reactor.

Working of a nuclear reactor:

• In a nuclear reactor, U²³⁵ or U²³⁹, a fissionable material is stacked with heavy water (D₂O deuterium oxide) or graphite called moderator.
• The neutrons produced in the fission pass through the moderator and lose a part of their energy. The slow neutrons produced during the process are captured which initiate new fission.
• Cadmium rods are inserted in the moderator as they have ability to absorb neutrons. This controls the rate of chain reaction.
• The energy released during the reaction appears as heat and removed by circulating a liquid (coolant). The coolant which has absorbed excess of heat from the reactor is passed over a heat exchanger for producing steam.
• Steam is then passed through the turbines to produce electricity. Thus, the atomic energy produced with the use of fission reaction can be controlled in the nuclear reactor.
• This process can be explored for peaceful purpose such as conversion of atomic energy into electrical energy which can be used for civilian purposes, ships, submarines, etc.

Note: Schematic diagram of nuclear power plant:

Question 73.
Why cadmium rods are used in nuclear reactor?
Answer:
Cadmium rods are inserted in the moderator as they have ability to absorb neutrons which help to control the rate of chain reaction.

Question 74.
Why short-lived isotopes are used for diagnostic purposes?
Answer:
For diagnostic purpose, short-lived isotopes are used in order to limit the exposure time to radiation. Note: Diagnostic Radioisotopes are listed below:

Question 75.
Give one application of therapeutic radioisotopes.
Answer:
Therapeutic radioisotopes are used to destroy abnormal cell growth in the body, e.g. cancerous cells.
Note: Therapeutic Radioisotopes are listed below:

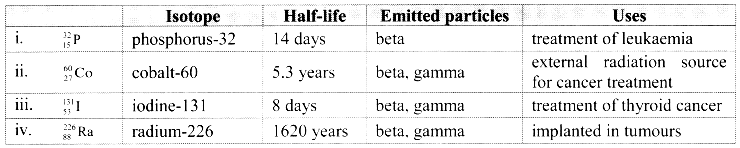
Question 76.
Give example of isotopes used in following.
i. Isotope used in the treatment of leukaemia.
ii. Isotopes used in the preservation of agricultural products by irradiation.
Answer:
i. Isotope of phosphorus, \({ }_{15}^{35} \mathrm{P}\).
ii. ⁶⁰Co or ¹³⁷Cs

Question 77.
At which places has BARC Mumbai set up irradiation plants for preservation of agricultural produce?
Answer:
Bhabha Atomic Research Centre (BARC) Mumbai has set up irradiation plants for preservation of agricultural produce such as mangoes, onion and potatoes at Vashi (Navi Mumbai) and Lasalgaon (Nashik).

Question 78.
Why radiotracer technique is used in chemistry?
Answer:
Radiotracer technique is used to trace the path/mechanism followed by a reaction in the system.

Question 79.
The half-life for radioactive decay of an element X is 140 days. Complete the following flow chart showing decay of 1 g of X.

Answer:

Shortcut method:
Amount of the element X left after n half-lives is given as [X] = \(\frac{[\mathrm{X}]_{0}}{2^{n}}\)
e.g. \(\frac{1}{2^{4}} \mathrm{~g}=\frac{1}{16} \mathrm{~g}\)

Question 80.
A sample of 35S complete its 10% decay in 20 min, then calculate the time required to complete decay by 19%.
Answer:
When decay is 10 % complete, if N₀ = 100 , then N = 100 – 10 = 90 and t = 20 minutes
When decay is 19 % complete, N = 100 – 19 = 81
Substituting these values in formula we get,

Multiple Choice Questions

1. Radius of the nucleus is related to the mass number A by ………….
(A) R = R₀A^1/2
(B) R = R₀A
(C) R = R₀A²
(D) R = R₀A^1/3
Answer:
(D) R = R₀A^1/3

2. Which of the following nuclides has the magic number of both protons and neutrons?
(A) \({ }_{50}^{115} \mathrm{Sn}\)
(B) \({ }_{81}^{206} \mathrm{Pb}\)
(C) \({ }_{82}^{208} \mathrm{Pb}\)
(D) \({ }_{50}^{118} \mathrm{Pb}\)
Answer:
(C) \({ }_{82}^{208} \mathrm{Pb}\)

3. The probability of decay of a radioactive element depends on …………..
i. the age of nucleus
ii. the presence of catalyst
iii. pressure
iv. temperature
(A) only i. and iv
(B) all of these
(C) only ii. And iii.
(D) none of these
Answer:
(D) none of these

4. The decay constant for 67Ga is 7.0 × 10^-4 s^-1. If initial concentration of is 0.07 g, what is the half-life of ⁶⁷Ga?
(A) 990 s
(B) 79.2 s
(C) 12375 s
(D) 10.10 × 10^-4 s
Answer:
(A) 990 s

5. The half-life of radioactive element X having decay constant of 1.7 × 10^-5 s^-1 is …………
(A) 21.5 h
(B) 19.7 h
(C) 11.3 h
(D) 2.8 h
Answer:
(C) 11.3 h

6. A radioactive decay of element X (Z = 90) is 30 % complete in 30 minutes. It has a half-life period of ……………
(A) 24.3 min
(B) 58.3 min
(C) 102.3 min
(D) 120.3 min
Answer:
(B) 58.3 min

7. The half-life of radium is 1600 years. The fraction of a sample of radium that would remain after 6400 year is ……….
(A) \(\frac {1}{2}\)
(B) \(\frac {1}{4}\)
(C) \(\frac {1}{8}\)
(D) \(\frac {1}{16}\)
Answer:
(D) \(\frac {1}{16}\)

8. The half-life of an element is 5 d. How much time is required for the decay of 7/8^th of the sample?
(A) 5 d
(B) 10 d
(C) 15 d
(D) 35/8 d
Answer:
(C) 15 d

9. The composition of an α-particle can be expressed as ……………….
(A) 1p + 1n
(B) 1p + 2n
(C) 2p + 1n
(D) 2p + 2n
Answer:
(D) 2p + 2n

10. If a radioactive nuclide of group 15 element undergoes β-particle emission, the daughter element will be found in ………………..
(A) 16 group
(B) 14 group
(C) 13 group
(D) same group
Answer:
(A) 16 group