Balbharti 12th Maharashtra State Board Maths Solutions Book Pdf Chapter 7 Linear Programming Ex 7.3 Questions and Answers.
Maharashtra State Board 12th Maths Solutions Chapter 7 Linear Programming Ex 7.3
Question 1.
A manufacturing firm produces two types of gadgets A and B, which are first processed in the foundry and then sent to machine shop for finishing. The number of man hours of labour required in each shop for production of A and B per unit and the number of man hours available for the firm are as follows :
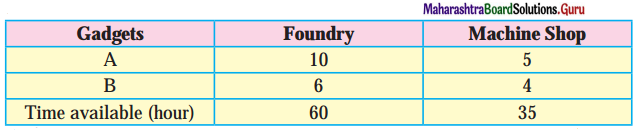
Profit on the sale of A is ₹ 30 and B is ₹ 20 per units. Formulate the L.P.P. to have maximum profit.
Solution:
Let the number of gadgets A produced by the firm be x and the number of gadgets B produced by the firm be y.
The profit on the sale of A is ₹ 30 per unit and on the sale of B is ₹ 20 per unit.
∴ total profit is z = 30x + 20y.
This is a linear function which is to be maximized. Hence it is the objective function.
The constraints are as per the following table :
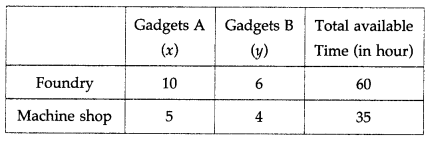
From the table total man hours of labour required for x units of gadget A and y units of gadget B in foundry is (10x + 6y) hours and total man hours of labour required in machine shop is (5x + 4y) hours.
Since, maximum time avilable in foundry and machine shops are 60 hours and 35 hours respectively.
Therefore, the constraints are 10x + 6y ≤ 60, 5x + 4y ≤ 35. Since, x and y cannot be negative, we have x ≥ 0, y ≥ 0. Hence, the given LPP can be formulated as :
Maximize z = 30x + 20y, subject to 10x + 6y ≤ 60, 5x + 4y ≤ 35, x ≥ 0, y ≥ 0.
Question 2.
In a cattle breading firm, it is prescribed that the food ration for one animal must contain 14, 22 and 1 units of nutrients A, B and C respectively. Two different kinds of fodder are available. Each unit of these two contains the following amounts of these three nutrients :
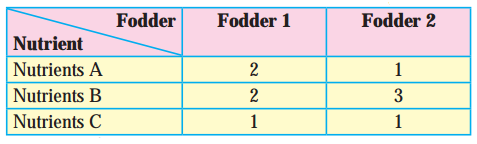
The cost of fodder 1 is ₹3 per unit and that of fodder ₹ 2, Formulate the L.P.P. to minimize the cost.
Solution:
Let x units of fodder 1 and y units of fodder 2 be prescribed.
The cost of fodder 1 is ₹ 3 per unit and cost of fodder 2 is ₹ 2 per unit.
∴ total cost is z = 3x + 2y
This is the linear function which is to be minimized. Hence it is the objective function. The constraints are as per the following table :
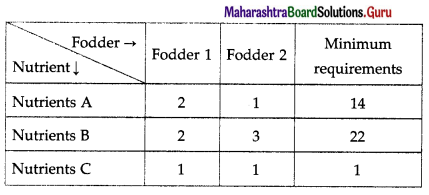
From table fodder contains (2x + y) units of nutrients A, (2x + 3y) units of nutrients B and (x + y) units of nutrients C. The minimum requirements of these nutrients are 14 units, 22 units and 1 unit respectively.
Therefore, the constraints are
2x + y ≥ 14, 2x + 3y ≥ 22, x + y ≥ 1
Since, number of units (i.e. x and y) cannot be negative, we have, x ≥ 0, y ≥ 0.
Hence, the given LPP can be formulated as
Minimize z = 3x + 2y, subject to
2x + y ≥ 14, 2x + 3y ≥ 22, x + y ≥ 1, x ≥ 0, y ≥ 0.
![]()
Question 3.
A company manufactures two types of chemicals A and B. Each chemical requires two types of raw material P and Q. The table below shows number of units of P and Q required to manufacture one unit of A and one unit of B and the total availability of P and Q.

The company gets profits of ₹350 and ₹400 by selling one unit of A and one unit of B respectively. (Assume that the entire production of A and B can be sold). How many units of the chemicals A and B should be manufactured so that the company get maximum profit? Formulate the problem as L.P.P. to maximize the profit.
Solution:
Let the company manufactures x units of chemical A and y units of chemical B. Then the total profit f to the company is p = ₹ (350x + 400y).
This is a linear function which is to be maximized.
Hence, it is the objective function.
The constraints are as per the following table:
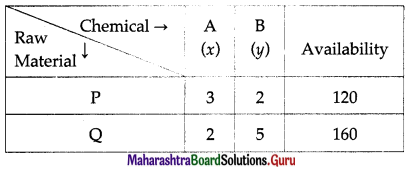
The raw material P required for x units of chemical A and y units of chemical B is 3x + 2y. Since, the maximum availability of P is 120, we have the first constraint as 3x + 2y ≤ 120.
Similarly, considering the raw material Q, we have : 2x + 5y ≤ 160.
Since, x and y cannot be negative, we have, x ≥ 0, y ≥ 0.
Hence, the given LPP can be formulated as :
Maximize p = 350x + 400y, subject to
3x + 2y ≤ 120, 2x + 5y ≤ 160, x ≥ 0, y ≥ 0.
Question 4.
A printing company prints two types of magazines A and B. The company earns ₹ 10 and ₹ 15 on magazines A and B per copy. These are processed on three machines I, II, III. Magazine A requires 2 hours on Machine I, 5 hours on Machine II and 2 hours on Machine III. Magazine B requires 3 hours on Machine I, 2 hours on Machine II and 6 hours on Machine III. Machines I, II, III are available for 36, 50, 60 hours per week respectively. Formulate the L.P.P. to determine weekly production of A and B, so that the total profit is maximum.
Solution:
Let the company prints x magazine of type A and y magazine of type B.
Profit on sale of magazine A is ₹ 10 per copy and magazine B is ₹ 15 per copy.
Therefore, the total earning z of the company is
z = ₹ (10x + 15y).
This is a linear function which is to be maximized.
Hence, it is the objective function.
The constraints are as per the following table:
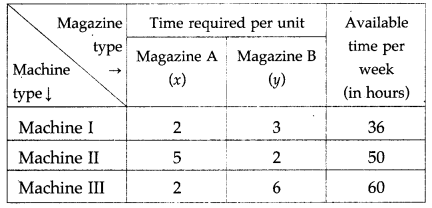
From the table, the total time required for Machine I is (2x + 3y) hours, for Machine II is (5x + 2y) hours and for Machine III is (2x + 6y) hours. The machines I, II, III are available for 36,50 and 60 hours per week. Therefore, the constraints are 2x + 3y ≤ 36, 5x + 2y ≤ 50, 2x + 6y ≤ 60.
Since x and y cannot be negative. We have, x ≥ 0, y ≥ 0. Hence, the given LPP can be formulated as :
Maximize z = 10x + 15y, subject to
2x + 3y ≤ 36, 5x + 2y ≤ 50, 2x + 6y ≤ 60, x ≥ 0, y ≥ 0.
![]()
Question 5.
A manufacture produces bulbs and tubes. Each of these must be processed through two machines M1 and M2. A package of bulbs require 1 hour of work on Machine M1 and 3 hours of work on M2. A package of tubes require 2 hours on Machine M1 and 4 hours on Machine M2. He earns a profit of ₹ 13.5 per package of bulbs and ₹ 55 per package of tubes. Formulate the LLP to maximize the profit, if he operates the machine M1, for atmost 10 hours a day and machine M2 for atmost 12 hours a day.
Solution:
Let the number of packages of bulbs produced by manufacturer be x and packages of tubes be y. The manufacturer earns a profit of ₹ 13.5 per package of bulbs and ₹ 55 per package of tubes.
Therefore, his total profit is p = ₹ (13.5x + 55y)
This is a linear function which is to be maximized.
Hence, it is the objective function.
The constraints are as per the following table :

From the table, the total time required for Machine M1 is (x + 2y) hours and for Machine M2 is (3x + 4y) hours.
Given Machine M1 and M2 are available for atmost 10 hours and 12 hours a day respectively.
Therefore, the constraints are x + 2y ≤ 10, 3x + 4y ≤ 12. Since, x and y cannot be negative, we have, x ≥ 0, y ≥ 0. Hence, the given LPP can be formulated as :
Maximize p = 13.5x + 55y, subject to x + 2y ≤ 10, 3x + 4y ≤ 12, x ≥ 0, y ≥ 0.
Question 6.
A company manufactures two types of fertilizers F1 and F2. Each type of fertilizer requires
two raw materials A and B. The number of units of A and B required to manufacture one unit of fertilizer F1 and F2 and availability of the raw materials A and B per day are given in the
table below :

By selling one unit of F1 and one unit of F2, company gets a profit of ₹ 500 and ₹ 750
respectively. Formulate the problem as L.P.P. to maximize the profit.
Solution:
Let the company manufactures x units of fertilizers F1 and y units of fertilizers F1. Then the total profit to the company is
z = ₹(500x + 750y).
This is a linear function that is to be maximized. Hence, it is an objective function.
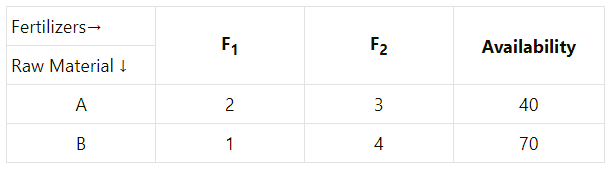
The raw material A required for x units of Fertilizers F1 and y units of Fertilizers F2 is 2x + Since the maximum availability of A is 40, we have the first constraint as 2x + 3y ≤ 40.
Similarly, considering the raw material B, we have x + 4y ≤ 70.
Since, x and y cannot be negative, we have, x ≥ 0, y ≥ 0.
Hence, the given LPP can be formulated as:
Maximize z = 500x + 750y, subject to
2x + 3y ≤ 40, x + 4y ≤ 70, x ≥ 0, y ≥ 0.
![]()
Question 7.
A doctor has prescribed two different units of foods A and B to form a weekly diet for a sick person. The minimum requirements of fats, carbohydrates and proteins are 18, 28, 14 units respectively. One unit of food A has 4 units of fats. 14 units of carbohydrates and 8 units of protein. One unit of food B has 6 units of fat, 12 units of carbohydrates and 8 units of protein. The price of food A is ₹ 4.5 per unit and that of food B is ₹ 3.5 per unit. Form the L.P.P. so that the sick person’s diet meets the requirements at a minimum cost.
Solution:
Let the diet of sick person include x units of food A and y units of food B.
Then x ≥ 0, y ≥ 0.
The prices of food A and B are ₹ 4.5 and ₹ 3.5 per unit respectively.
Therefore, the total cost is z = ₹ (4.5x + 3.5y)
This is the linear function which is to be minimized.
Hence, it is objective function.
The constraints are as per the following table :
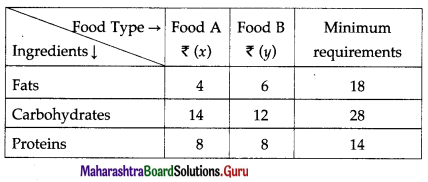
From the table, the sick person’s diet will include (4x + 6y) units of fats, (14x + 12y) units of carbohydrates and (8x + 8y) units of proteins. The minimum requirements of these ingredients are 18 units, 28 units and 14 units respectively.
Therefore, the constraints are
4x + 6y ≥ 18, 14x + 12y ≥ 28, 8x + 8y ≥ 14.
Hence, the given LPP can be formulated as
Minimize z = 4.5x + 3.5y, subject to
4x + 6y ≥ 18, 14x + 12y ≥ 28, 8x + 8y ≥ 14, x ≥ 0, y ≥ 0.
Question 8.
If John drives a car at a speed of 60 kms/hour he has to spend ₹ 5 per km on petrol. If he drives at a faster speed of 90 kms/hour, the cost of petrol increases to ₹ 8 per km. He has ₹ 600 to spend on petrol and wishes to travel the maximum distance within an hour. Formulate the above problem as L.P.P.
Solution:
Let John travel xl km at a speed of 60 km/ hour and x1 km at a speed of 90 km/hour.
Therefore, time required to travel a distance of x1 km is \(\frac{x_{1}}{60}\) hours and the time required to travel a distance of
x2 km is \(\frac{x_{2}}{90}\) hours.
∴ total time required to travel is \(\left(\frac{x_{1}}{60}+\frac{x_{2}}{90}\right)\) hours.
Since he wishes to travel the maximum distance within an hour,
\(\frac{x_{1}}{60}+\frac{x_{2}}{90}\) ≤ 1
He has to spend ₹ 5 per km on petrol at a speed of 60 km/hour and ₹ 8 per km at a speed of 90 km/hour.
∴ the total cost of travelling is ₹ (5x1 + 8x2)
Since he has ₹ 600 to spend on petrol,
5x1 + 8x2 ≤ 600
Since distance is never negative, x1 ≥ 0, x2 ≥ 0.
Total distance travelled by John is z. = (x1 + x2) km.
This is the linear function which is to be maximized.
Hence, it is objective function.
Hence, the given LPP can be formulated as :
Maximize z = x1 + x2, subject to
\(\frac{x_{1}}{60}+\frac{x_{2}}{90}\) ≤ 1, 5x1 + 8x2 ≤ 600, x1 ≥ 0, x2 ≥ 0.
![]()
Question 9.
The company makes concrete bricks made up of cement and sand. The weight of a concrete brick has to be least 5 kg. Cement costs ₹ 20 per kg. and sand costs of ₹ 6 per kg. strength consideration dictate that a concrete brick should contain minimum 4 kg. of cement and not more than 2 kg. of sand. Form the L.P.P. for the cost to be minimum.
Solution:
Let the company use x1 kg of cement and x2 kg of sand to make concrete bricks.
Cement costs ₹ 20 per kg and sand costs ₹ 6 per kg.
∴ the total cost c = ₹ (20x1 + 6x2)
This is a linear function which is to be minimized.
Hence, it is the objective function.
Total weight of brick = (x1 + x2) kg
Since the weight of concrete brick has to be at least 5 kg,
∴ x1 + x2 ≥ 5.
Since concrete brick should contain minimum 4 kg of cement and not more than 2 kg of sand,
x1 ≥ 4 and 0 ≤ x2 ≤ 2
Hence, the given LPP can be formulated as :
Minimize c = 20x1 + 6x2, subject to
x1 + x2 ≥ 5, x1 ≥ 4, 0 ≤ x2 ≤ 2.