Balbharti 12th Maharashtra State Board Maths Solutions Book Pdf Chapter 6 Differential Equations Miscellaneous Exercise 6 Questions and Answers.
Maharashtra State Board 12th Maths Solutions Chapter 6 Differential Equations Miscellaneous Exercise 6
(I) Choose the correct option from the given alternatives:
Question 1.
The order and degree of the differential equation \(\sqrt{1+\left(\frac{d y}{d x}\right)^{2}}=\left(\frac{d^{2} y}{d x^{2}}\right)^{\frac{3}{2}}\) are respectively……..
(a) 2, 1
(b) 1, 2
(c) 3, 2
(d) 2, 3
Answer:
(d) 2, 3
Question 2.
The differential equation of y = c2 + \(\frac{c}{x}\) is…….
(a) \(x^{4}\left(\frac{d y}{d x}\right)^{2}-x \frac{d y}{d x}=y\)
(b) \(\frac{d y}{d x^{2}}+x \frac{d y}{d x}+y=0\)
(c) \(x^{3}\left(\frac{d y}{d x}\right)^{2}+x \frac{d y}{d x}=y\)
(d) \(\frac{d^{2} y}{d x^{2}}+\frac{d y}{d x}-y=0\)
Answer:
(a) \(x^{4}\left(\frac{d y}{d x}\right)^{2}-x \frac{d y}{d x}=y\)
![]()
Question 3.
x2 + y2 = a2 is a solution of ………
(a) \(\frac{d^{2} y}{d x^{2}}+\frac{d y}{d x}-y=0\)
(b) \(y=x \sqrt{1+\left(\frac{d y}{d x}\right)^{2}}+a^{2} y\)
(c) \(y=x \frac{d y}{d x}+a \sqrt{1+\left(\frac{d y}{d x}\right)^{2}}\)
(d) \(\frac{d^{2} y}{d x^{2}}=(x+1) \frac{d y}{d x}\)
Answer:
(c) \(y=x \frac{d y}{d x}+a \sqrt{1+\left(\frac{d y}{d x}\right)^{2}}\)

Question 4.
The differential equation of all circles having their centres on the line y = 5 and touching the X-axis is
(a) \(y^{2}\left(1+\frac{d y}{d x}\right)=25\)
(b) \((y-5)^{2}\left[1+\left(\frac{d y}{d x}\right)^{2}\right]=25\)
(c) \((y-5)^{2}+\left[1+\left(\frac{d y}{d x}\right)^{2}\right]=25\)
(d) \((y-5)^{2}\left[1-\left(\frac{d y}{d x}\right)^{2}\right]=25\)
Answer:
(b) \((y-5)^{2}\left[1+\left(\frac{d y}{d x}\right)^{2}\right]=25\)

Question 5.
The differential equation y \(\frac{d y}{d x}\) + x = 0 represents family of ………
(a) circles
(b) parabolas
(c) ellipses
(d) hyperbolas
Answer:
(a) circles
Hint:
y \(\frac{d y}{d x}\) + x = 0
∴ ∫y dy + ∫x dx = c
∴ \(\frac{y^{2}}{2}+\frac{x^{2}}{2}=c\)
∴ x2 + y2 = 2c which is a circle.
![]()
Question 6.
The solution of \(\frac{1}{x} \cdot \frac{d y}{d x}=\tan ^{-1} x\) is……
(a) \(\frac{x^{2} \tan ^{-1} x}{2}+c=0\)
(b) x tan-1x + c = 0
(c) x – tan-1x = c
(d) \(y=\frac{x^{2} \tan ^{-1} x}{2}-\frac{1}{2}\left(x-\tan ^{-1} x\right)+c\)
Answer:
(d) \(y=\frac{x^{2} \tan ^{-1} x}{2}-\frac{1}{2}\left(x-\tan ^{-1} x\right)+c\)

Question 7.
The solution of (x + y)2 \(\frac{d y}{d x}\) = 1 is…….
(a) x = tan-1(x + y) + c
(b) y tan-1(\(\frac{x}{y}\)) = c
(c) y = tan-1(x + y) + c
(d) y + tan-1(x + y) = c
Answer:
(c) y = tan-1(x + y) + c

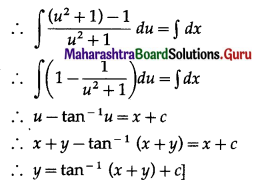
Question 8.
The Solution of \(\frac{d y}{d x}=\frac{y+\sqrt{x^{2}-y^{2}}}{2}\) is……
(a) sin-1(\(\frac{y}{x}\)) = 2 log |x| + c
(b) sin-1(\(\frac{y}{x}\)) = log |x| + c
(c) sin(\(\frac{x}{y}\)) = log |x| + c
(d) sin(\(\frac{y}{x}\)) = log |y| + c
Answer:
(b) sin-1(\(\frac{y}{x}\)) = log |x| + c

Question 9.
The solution of \(\frac{d y}{d x}\) + y = cos x – sin x is……
(a) y ex = cos x + c
(b) y ex + ex cos x = c
(c) y ex = ex cos x + c
(d) y2 ex = ex cos x + c
Answer:
(c) y ex = ex cos x + c
Hint:
\(\frac{d y}{d x}\) + y = cos x – sin x
I.F. = \(e^{\int 1 d x}=e^{x}\)
∴ the solution is y . ex = ∫(cos x – sin x) ex + c
∴ y . ex = ex cos x + c
![]()
Question 10.
The integrating factor of linear differential equation x \(\frac{d y}{d x}\) + 2y = x2 log x is……..
(a) \(\frac{1}{x}\)
(b) k
(c) \(\frac{1}{n^{2}}\)
(d) x2
Answer:
(d) x2
Hint:
I.F. = \(e^{\int \frac{2}{x} d x}\)
= e2 log x
= x2
Question 11.
The solution of the differential equation \(\frac{d y}{d x}\) = sec x – y tan x is…….
(a) y sec x + tan x = c
(b) y sec x = tan x + c
(c) sec x + y tan x = c
(d) sec x = y tan x + c
Answer:
(b) y sec x = tan x + c
Hint:
\(\frac{d y}{d x}\) = sec x – y tan x
∴ \(\frac{d y}{d x}\) + y tan x = sec x
I.F. = \(e^{\int \tan x d x}=e^{\log \sec x}\) = sec x
∴ the solution is
y . sec x = ∫sec x . sec x dx + c
∴ y sec x = tan x + c
Question 12.
The particular solution of \(\frac{d y}{d x}=x e^{y-x}\), when x = y = 0 is……
(a) ex-y = x + 1
(b) ex+y = x + 1
(c) ex + ey = x + 1
(d) ey-x = x – 1
Answer:
(a) ex-y = x + 1

![]()
Question 13.
\(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1\) is a solution of……..
(a) \(\frac{d^{2} y}{d x^{2}}+y x+\left(\frac{d y}{d x}\right)^{2}=0\)
(b) \(x y \frac{d^{2} y}{d x^{2}}+2\left(\frac{d y}{d x}\right)^{2}-y \frac{d y}{d x}=0\)
(c) \(y \frac{d^{2} y}{d x^{2}}+2\left(\frac{d y}{d x}\right)^{2}+y=0\)
(d) \(x y \frac{d y}{d x}+y \frac{d^{2} y}{d x^{2}}=0\)
Answer:
(b) \(x y \frac{d^{2} y}{d x^{2}}+2\left(\frac{d y}{d x}\right)^{2}-y \frac{d y}{d x}=0\)

Question 14.
The decay rate of certain substances is directly proportional to the amount present at that instant. Initially, there are 27 grams of substance and 3 hours later it is found that 8 grams left. The amount left after one more hour is……
(a) 5\(\frac{2}{3}\) grams
(b) 5\(\frac{1}{3}\) grams
(c) 5.1 grams
(d) 5 grams
Answer:
(b) 5\(\frac{1}{3}\) grams
Question 15.
If the surrounding air is kept at 20°C and the body cools from 80°C to 70°C in 5 minutes, the temperature of the body after 15 minutes will be…..
(a) 51.7°C
(b) 54.7°C
(c) 52.7°C
(d) 50.7°C
Answer:
(b) 54.7°C
(II) Solve the following:
Question 1.
Determine the order and degree of the following differential equations:
(i) \(\frac{d^{2} y}{d x^{2}}+5 \frac{d y}{d x}+y=x^{3}\)
Solution:
The given D.E. is \(\frac{d^{2} y}{d x^{2}}+5 \frac{d y}{d x}+y=x^{3}\)
This D.E. has highest order derivative \(\frac{d^{2} y}{d x^{2}}\) with power 1.
∴ the given D.E. is of order 2 and degree 1.
(ii) \(\left(\frac{d^{3} y}{d x^{3}}\right)^{2}=\sqrt[5]{1+\frac{d y}{d x}}\)
Solution:
The given D.E. is \(\left(\frac{d^{3} y}{d x^{3}}\right)^{2}=\sqrt[5]{1+\frac{d y}{d x}}\)
\(\left(\frac{d^{3} y}{d x^{3}}\right)^{2 \times 5}=1+\frac{d y}{d x}\)
\(\left(\frac{d^{3} y}{d x^{3}}\right)^{10}=1+\frac{d y}{d x}\)
This D.E. has highest order derivative \(\frac{d^{3} y}{d x^{3}}\) with power 10.
∴ the given D.E. is of order 3 and degree 10.
(iii) \(\sqrt[3]{1+\left(\frac{d y}{d x}\right)^{2}}=\frac{d^{2} y}{d x^{2}}\)
Solution:
The given D.E. is \(\sqrt[3]{1+\left(\frac{d y}{d x}\right)^{2}}=\frac{d^{2} y}{d x^{2}}\)
On cubing both sides, we get
\(1+\left(\frac{d y}{d x}\right)^{2}=\left(\frac{d^{2} y}{d x^{2}}\right)^{3}\)
This D.E. has highest order derivative \(\frac{d^{2} y}{d x^{2}}\) with power 3.
∴ the given D.E. is of order 2 and degree 3.
![]()
(iv) \(\frac{d y}{d x}=3 y+\sqrt[4]{1+5\left(\frac{d y}{d x}\right)^{2}}\)
Solution:
The given D.E. is
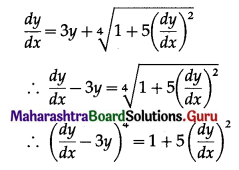
This D.E. has the highest order derivative \(\frac{d y}{d x}\) with power 4.
∴ the given D.E. is of order 1 and degree 4.
(v) \(\frac{d^{4} y}{d x^{4}}+\sin \left(\frac{d y}{d x}\right)=0\)
Solution:
The given D.E. is \(\frac{d^{4} y}{d x^{4}}+\sin \left(\frac{d y}{d x}\right)=0\)
This D.E. has highest order derivative \(\frac{d^{4} y}{d x^{4}}\).
∴ order = 4
Since this D.E. cannot be expressed as a polynomial in differential coefficient, the degree is not defined.
Question 2.
In each of the following examples verify that the given function is a solution of the differential equation.
(i) \(x^{2}+y^{2}=r^{2} ; x \frac{d y}{d x}+r \sqrt{1+\left(\frac{d y}{d x}\right)^{2}}=y\)
Solution:
x2 + y2 = r2 ……. (1)
Differentiating both sides w.r.t. x, we get
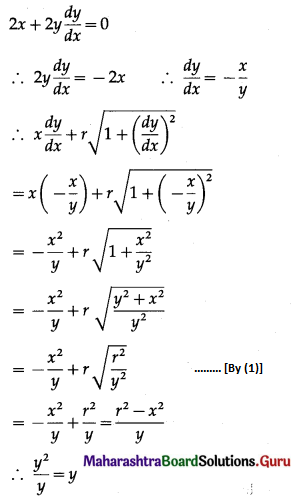
Hence, x2 + y2 = r2 is a solution of the D.E.
\(x \frac{d y}{d x}+r \sqrt{1+\left(\frac{d y}{d x}\right)^{2}}=y\)
(ii) y = eax sin bx; \(\frac{d^{2} y}{d x^{2}}-2 a \frac{d y}{d x}+\left(a^{2}+b^{2}\right) y=0\)
Solution:
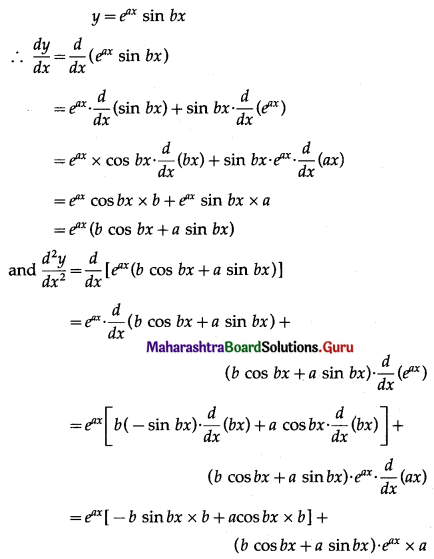
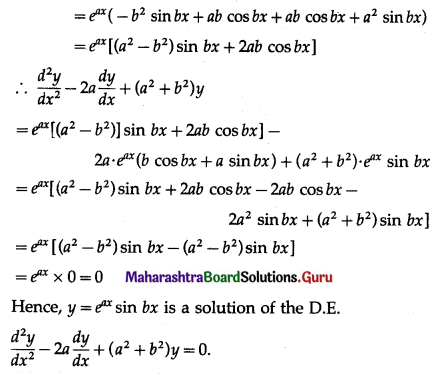
(iii) y = 3 cos(log x) + 4 sin(log x); \(x^{2} \frac{d^{2} y}{d x^{2}}+x \frac{d y}{d x}+y=0\)
Solution:
y = 3 cos(log x) + 4 sin (log x) …… (1)
Differentiating both sides w.r.t. x, we get
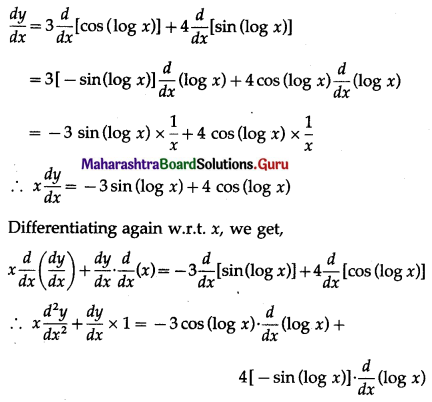
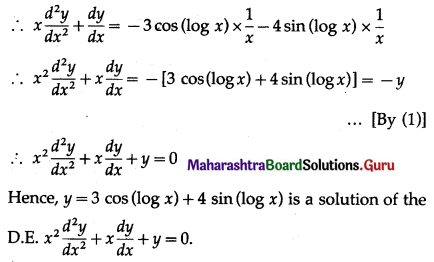
![]()
(iv) xy = aex + be-x + x2; \(x \frac{d^{2} y}{d x^{2}}+2 \frac{d y}{d x}+x^{2}=x y+2\)
Solution:

(v) x2 = 2y2 log y, x2 + y2 = xy \(\frac{d x}{d y}\)
Solution:
x2 = 2y2 log y ……(1)
Differentiating both sides w.r.t. y, we get

∴ x2 + y2 = xy \(\frac{d x}{d y}\)
Hence, x2 = 2y2 log y is a solution of the D.E.
x2 + y2 = xy \(\frac{d x}{d y}\)
Question 3.
Obtain the differential equation by eliminating the arbitrary constants from the following equations:
(i) y2 = a(b – x)(b + x)
Solution:
y2 = a(b – x)(b + x) = a(b2 – x2)
Differentiating both sides w.r.t. x, we get
2y \(\frac{d y}{d x}\) = a(0 – 2x) = -2ax
∴ y \(\frac{d y}{d x}\) = -ax …….(1)
Differentiating again w.r.t. x, we get
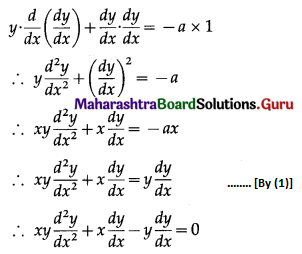
This is the required D.E.
(ii) y = a sin(x + b)
Solution:
y = a sin(x + b)
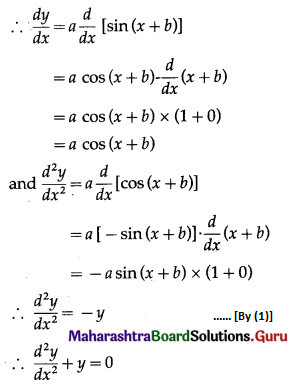
This is the required D.E.
(iii) (y – a)2 = b(x + 4)
Solution:
(y – a)2 = b(x + 4) …….(1)
Differentiating both sides w.r.t. x, we get
\(2(y-a) \cdot \frac{d}{d x}(y-a)=b \frac{d}{d x}(x+4)\)

![]()
(iv) y = \(\sqrt{a \cos (\log x)+b \sin (\log x)}\)
Solution:
y = \(\sqrt{a \cos (\log x)+b \sin (\log x)}\)
∴ y2 = a cos (log x) + b sin (log x) …….(1)
Differentiating both sides w.r.t. x, we get

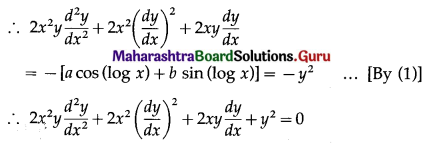
(v) y = Ae3x+1 + Be-3x+1
Solution:
y = Ae3x+1 + Be-3x+1 …… (1)
Differentiating twice w.r.t. x, we get

This is the required D.E.
Question 4.
Form the differential equation of:
(i) all circles which pass through the origin and whose centres lie on X-axis.
Solution:
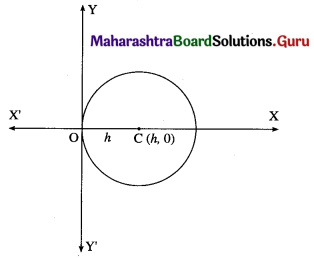
Let C (h, 0) be the centre of the circle which pass through the origin. Then radius of the circle is h.
∴ equation of the circle is (x – h)2 + (y – 0)2 = h2
∴ x2 – 2hx + h2 + y2 = h2
∴ x2 + y2 = 2hx ……..(1)
Differentiating both sides w.r.t. x, we get
2x + 2y \(\frac{d y}{d x}\) = 2h
Substituting the value of 2h in equation (1), we get
x2 + y2 = (2x + 2y \(\frac{d y}{d x}\)) x
∴ x2 + y2 = 2x2 + 2xy \(\frac{d y}{d x}\)
∴ 2xy \(\frac{d y}{d x}\) + x2 – y2 = 0
This is the required D.E.
(ii) all parabolas which have 4b as latus rectum and whose axis is parallel to Y-axis.
Solution:
Let A(h, k) be the vertex of the parabola which has 4b as latus rectum and whose axis is parallel to the Y-axis.
Then equation of the parabola is
(x – h)2 = 4b(y – k) ……. (1)
where h and k are arbitrary constants.
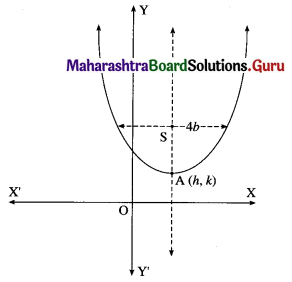
Differentiating both sides of (1) w.r.t. x, we get
2(x – h). \(\frac{d}{d x}\)(x – h) = 4b . \(\frac{d}{d x}\)(y – k)
∴ 2(x – h) x (1 – 0) = 4b(\(\frac{d y}{d x}\) – 0)
∴ (x – h) = 2b \(\frac{d y}{d x}\)
Differentiating again w.r.t. x, we get
1 – 0 = 2b \(\frac{d^{2} y}{d x^{2}}\)
∴ 2b \(\frac{d^{2} y}{d x^{2}}\) – 1 = 0
This is the required D.E.
![]()
(iii) an ellipse whose major axis is twice its minor axis.
Solution:
Let 2a and 2b be lengths of the major axis and minor axis of the ellipse.
Then 2a = 2(2b)
∴ a = 2b
∴ equation of the ellipse is
\(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1\)
∴ \(\frac{x^{2}}{(2 b)^{2}}+\frac{y^{2}}{b^{2}}=1\)
∴ \(\frac{x^{2}}{4 b^{2}}+\frac{y^{2}}{b^{2}}=1\)
∴ x2 + 4y2 = 4b2
Differentiating w.r.t. x, we get
2x + 4 × 2y \(\frac{d y}{d x}\) = 0
∴ x + 4y \(\frac{d y}{d x}\) = 0
This is the required D.E.
(iv) all the lines which are normal to the line 3x + 2y + 7 = 0.
Solution:
Slope of the line 3x – 2y + 7 = 0 is \(\frac{-3}{-2}=\frac{3}{2}\).
∴ slope of normal to this line is \(-\frac{2}{3}\)
Then the equation of the normal is
y = \(-\frac{2}{3}\)x + k, where k is an arbitrary constant.
Differentiating w.r.t. x, we get
\(\frac{d y}{d x}=-\frac{2}{3} \times 1+0\)
∴ 3\(\frac{d y}{d x}\) + 2 = 0
This is the required D.E.
(v) the hyperbola whose length of transverse and conjugate axes are half of that of the given hyperbola \(\frac{x^{2}}{16}-\frac{y^{2}}{36}=k\).
Solution:
The equation of the hyperbola is \(\frac{x^{2}}{16}-\frac{y^{2}}{36}=k\)
i.e., \(\frac{x^{2}}{16 k}-\frac{y^{2}}{36 k}=1\)
Comparing this equation with \(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1\), we get
a2 = 16k, b2 = 36k
∴ a = 4√k, b = 6√k
∴ l(transverse axis) = 2a = 8√k
and l(conjugate axis) = 2b = 12√k
Let 2A and 2B be the lengths of the transverse and conjugate axes of the required hyperbola.
Then according to the given condition
2A = a = 4√k and 2B = b = 6√k
∴ A = 2√k and B = 3√k
∴ equation of the required hyperbola is
\(\frac{x^{2}}{A^{2}}-\frac{y^{2}}{B^{2}}=1\)
i.e., \(\frac{x^{2}}{4 k}-\frac{y^{2}}{9 k}=1\)
∴ 9x2 – 4y2 = 36k, where k is an arbitrary constant.
Differentiating w.r.t. x, we get
9 × 2x – 4 × 2y \(\frac{d y}{d x}\) = 0
∴ 9x – 4y \(\frac{d y}{d x}\) = 0
This is the required D.E.
![]()
Question 5.
Solve the following differential equations:
(i) log(\(\frac{d y}{d x}\)) = 2x + 3y
Solution:
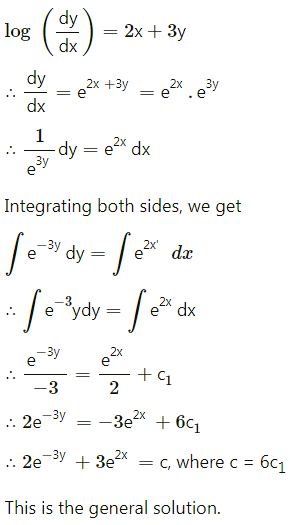
(ii) \(\frac{d y}{d x}\) = x2y + y
Solution:

(iii) \(\frac{d y}{d x}=\frac{2 y-x}{2 y+x}\)
Solution:



(iv) x dy = (x + y + 1) dx
Solution:


(v) \(\frac{d y}{d x}\) + y cot x = x2 cot x + 2x
Solution:
\(\frac{d y}{d x}\) + y cot x = x cot x + 2x ……..(1)
This is the linear differential equation of the form
\(\frac{d y}{d x}\) + Py = Q, where P = cot x and Q = x2 cot x + 2x
∴ I.F. = \(e^{\int P d x}\)
= \(e^{\int \cot x d x}\)
= \(e^{\log (\sin x)}\)
= sin x
∴ the solution of (1) is given by
y(I.F.) = ∫Q . (I.F.) dx + c
∴ y sin x = ∫(x2 cot x + 2x) sin x dx + c
∴ y sinx = ∫(x2 cot x . sin x + 2x sin x) dx + c
∴ y sinx = ∫x2 cos x dx + 2∫x sin x dx + c
∴ y sinx = x2 ∫cos x dx – ∫[\(\frac{d}{d x}\left(x^{2}\right)\) ∫cos x dx] dx + 2∫x sin x dx + c
∴ y sin x = x2 (sin x) – ∫2x(sin x) dx + 2∫x sin x dx + c
∴ y sin x = x2 sin x – 2∫x sin x dx + 2∫x sin x dx + c
∴ y sin x = x2 sin x + c
∴ y = x2 + c cosec x
This is the general solution.
![]()
(vi) y log y = (log y2 – x) \(\frac{d y}{d x}\)
Solution:


(vii) 4 \(\frac{d x}{d y}\) + 8x = 5e-3y
Solution:

Question 6.
Find the particular solution of the following differential equations:
(i) y(1 + log x) = (log xx) \(\frac{d y}{d x}\), when y(e) = e2
Solution:
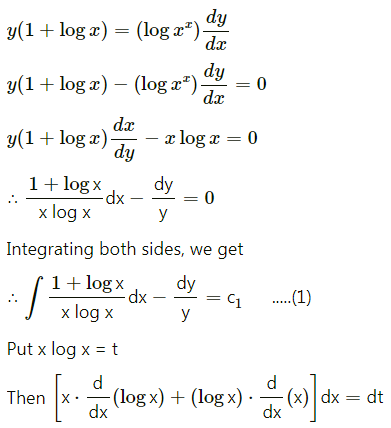

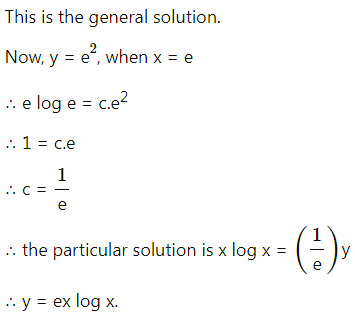
(ii) (x + 2y2) \(\frac{d y}{d x}\) = y, when x = 2, y = 1
Solution:


This is the general solution.
When x = 2, y = 1, we have
2 = 2(1)2 + c(1)
∴ c = 0
∴ the particular solution is x = 2y2.
![]()
(iii) \(\frac{d y}{d x}\) – 3y cot x = sin 2x, when y(\(\frac{\pi}{2}\)) = 2
Solution:
\(\frac{d y}{d x}\) – 3y cot x = sin 2x
\(\frac{d y}{d x}\) = (3 cot x) y = sin 2x ……..(1)
This is the linear differential equation of the form


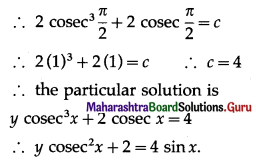
(iv) (x + y) dy + (x – y) dx = 0; when x = 1 = y
Solution:



(v) \(2 e^{\frac{x}{y}} d x+\left(y-2 x e^{\frac{x}{y}}\right) d y=0\), when y(0) = 1
Solution:
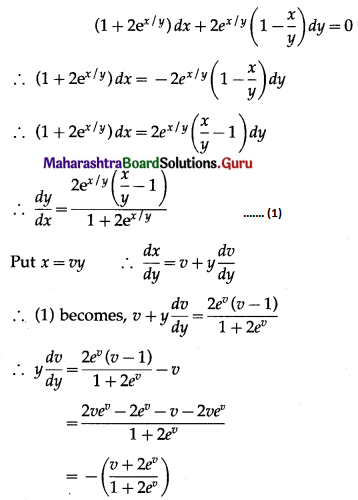

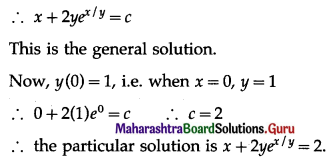
![]()
Question 7.
Show that the general solution of defferential equation \(\frac{d y}{d x}+\frac{y^{2}+y+1}{x^{2}+x+1}=0\) is given by (x + y + 1) = c(1 – x – y – 2xy).
Solution:



Question 8.
The normal lines to a given curve at each point (x, y) on the curve pass through (2, 0). The curve passes through (2, 3). Find the equation of the curve.
Solution:
Let P(x, y) be a point on the curve y = f(x).
Then slope of the normal to the curve is \(-\frac{1}{\left(\frac{d y}{d x}\right)}\)
∴ equation of the normal is

This is the general equation of the curve.
Since, the required curve passed through the point (2, 3), we get
22 + 32 = 4(2) + c
∴ c = 5
∴ equation of the required curve is x2 + y2 = 4x + 5.
![]()
Question 9.
The volume of a spherical balloon being inflated changes at a constant rate. If initially its radius is 3 units and after 3 seconds it is 6 units. Find the radius of the balloon after t seconds.
Solution:
Let r be the radius and V be the volume of the spherical balloon at any time t.
Then the rate of change in volume of the spherical balloon is \(\frac{d V}{d t}\) which is a constant.


Hence, the radius of the spherical balloon after t seconds is \((63 t+27)^{\frac{1}{3}}\) units.
![]()
Question 10.
A person’s assets start reducing in such a way that the rate of reduction of assets is proportional to the square root of the assets existing at that moment. If the assets at the beginning are ₹ 10 lakhs and they dwindle down to ₹ 10,000 after 2 years, show that the person will be bankrupt in 2\(\frac{2}{9}\) years from the start.
Solution:
Let x be the assets of the presort at time t years.
Then the rate of reduction is \(\frac{d x}{d t}\) which is proportional to √x.
∴ \(\frac{d x}{d t}\) ∝ √x
∴ \(\frac{d x}{d t}\) = -k√x, where k > 0
∴ \(\frac{d x}{\sqrt{x}}\) = -k dt
Integrating both sides, we get
\(\int x^{-\frac{1}{2}} d x\) = -k∫dt
∴ \(\frac{x^{\frac{1}{2}}}{\left(\frac{1}{2}\right)}\) = -kt + c
∴ 2√x = -kt + c
At the beginning, i.e. at t = 0, x = 10,00,000
2√10,00,000 = -k(0) + c
∴ c = 2000
∴ 2√x = -kt + 2000 ……..(1)
Also, when t = 2, x = 10,000
∴ 2√10000 = -k × 2 + 2000
∴ 2k = 1800
∴ k = 900
∴ (1) becomes,
∴ 2√x = -900t + 2000
When the person will be bankrupt, x = 0
∴ 0 = -900t + 2000
∴ 900t = 2000
∴ t = \(\frac{20}{9}=2 \frac{2}{9}\)
Hence, the person will be bankrupt in \(2 \frac{2}{9}\) years.