Balbharti 12th Maharashtra State Board Maths Solutions Book Pdf Chapter 6 Differential Equations Ex 6.5 Questions and Answers.
Maharashtra State Board 12th Maths Solutions Chapter 6 Differential Equations Ex 6.5
Question 1.
Solve the following differential equations:
(i) \(\frac{d y}{d x}+\frac{y}{x}=x^{3}-3\)
Solution:
\(\frac{d y}{d x}+\frac{y}{x}=x^{3}-3\) …….(1)
This is the linear differential equation of the form
\(\frac{d y}{d x}\) + P . y = Q, where P = \(\frac{1}{x}\) and Q = x3 – 3
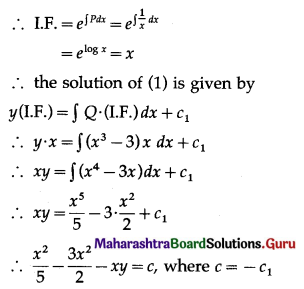
This is the general solution.
(ii) cos2x . \(\frac{d y}{d x}\) + y = tan x
Solution:


![]()
(iii) (x + 2y3) \(\frac{d y}{d x}\) = y
Solution:


(iv) \(\frac{d y}{d x}\) + y . sec x = tan x
Solution:
\(\frac{d y}{d x}\) + y sec x = tan x
∴ \(\frac{d y}{d x}\) + (sec x) . y = tan x ……..(1)
This is the linear differential equation of the form
\(\frac{d y}{d x}\) + P . y = Q, where P = sec x and Q = tan x
∴ I.F. = \(e^{\int P d x}\)
= \(e^{\int \sec x d x}\)
= \(e^{\log (\sec x+\tan x)}\)
= sec x + tan x
∴ the solution of (1) is given by
y (I.F.) = ∫Q . (I.F.) dx + c
∴ y(sec x + tan x) = ∫tan x (sec x + tan x) dx + c
∴ (sec x + tan x) . y = ∫(sec x tan x + tan2x) dx + c
∴ (sec x + tan x) . y = ∫(sec x tan x + sec2x – 1) dx + c
∴ (sec x + tan x) . y = sec x + tan x – x + c
∴ y(sec x + tan x) = sec x + tan x – x + c
This is the general solution.
![]()
(v) x \(\frac{d y}{d x}\) + 2y = x2 . log x
Solution:


(vi) (x + y) \(\frac{d y}{d x}\) = 1
Solution:
(x + y) \(\frac{d y}{d x}\) = 1
∴ \(\frac{d x}{d y}\) = x + y
∴ \(\frac{d x}{d y}\) – x = y
∴ \(\frac{d x}{d y}\) + (-1) x = y ……….(1)
This is the linear differential equation of the form

This is the general solution.
(vii) (x + a) \(\frac{d y}{d x}\) – 3y = (x + a)5
Solution:


![]()
(viii) dr + (2r cot θ + sin 2θ) dθ = 0
Solution:
dr + (2r cot θ + sin 2θ) dθ = 0
∴ \(\frac{d r}{d \theta}\) + (2r cot θ + sin 2θ) = 0
∴ \(\frac{d r}{d \theta}\) + (2 cot θ)r = -sin 2θ ………(1)
This is the linear differential equation of the form dr
\(\frac{d r}{d \theta}\) + P . r = Q, where P = 2 cot θ and Q = -sin 2θ

This is the general solution.
(ix) y dx + (x – y2) dy = 0
Solution:
y dx + (x – y2) dy = 0
∴ y dx = -(x – y2) dy
∴ \(\frac{d x}{d y}=-\frac{\left(x-y^{2}\right)}{y}=-\frac{x}{y}+y\)
∴ \(\frac{d x}{d y}+\left(\frac{1}{y}\right) \cdot x=y\) ………(1)
This is the linear differential equation of the form

This is the general solution.
(x) \(\left(1-x^{2}\right) \frac{d y}{d x}+2 x y=x\left(1-x^{2}\right)^{\frac{1}{2}}\)
Solution:


![]()
(xi) \(\left(1+x^{2}\right) \frac{d y}{d x}+y=e^{\tan ^{-1} x}\)
Solution:


Question 2.
Find the equation of the curve which passes through the origin and has the slope x + 3y – 1 at any point (x, y) on it.
Solution:
Let A(x, y) be the point on the curve y = f(x).
Then slope of the tangent to the curve at the point A is \(\frac{d y}{d x}\).
According to the given condition,
\(\frac{d y}{d x}\) = x + 3y – 1
∴ \(\frac{d y}{d x}\) – 3y = x – 1 ………(1)
This is the linear differential equation of the form

This is the general equation of the curve.
But the required curve is passing through the origin (0, 0).
∴ by putting x = 0 and y = 0 in (2), we get
0 = 2 + c
∴ c = -2
∴ from (2), the equation of the required curve is 3(x + 3y) = 2 – 2e3x i.e. 3(x + 3y) = 2 (1 – e3x).
![]()
Question 3.
Find the equation of the curve passing through the point \(\left(\frac{3}{\sqrt{2}}, \sqrt{2}\right)\) having slope of the tangent to the curve at any point (x, y) is \(-\frac{4 x}{9 y}\).
Solution:
Let A(x, y) be the point on the curve y = f(x).
Then the slope of the tangent to the curve at point A is \(\frac{d y}{d x}\).
According to the given condition
\(\frac{d y}{d x}=-\frac{4 x}{9 y}\)
∴ y dy = \(-\frac{4}{9}\) x dx
Integrating both sides, we get
∫y dy= \(-\frac{4}{9}\) ∫x dx
∴ \(\frac{y^{2}}{2}=-\frac{4}{9} \cdot \frac{x^{2}}{2}+c_{1}\)
∴ 9y2 = -4x2 + 18c1
∴ 4x2 + 9y2 = c where c = 18c1
This is the general equation of the curve.
But the required curve is passing through the point \(\left(\frac{3}{\sqrt{2}}, \sqrt{2}\right)\).
∴ by putting x = \(\frac{3}{\sqrt{2}}\) and y = √2 in (1), we get
\(4\left(\frac{3}{\sqrt{2}}\right)^{2}+9(\sqrt{2})^{2}=c\)
∴ 18 + 18 = c
∴ c = 36
∴ from (1), the equation of the required curve is 4x2 + 9y2 = 36.
Question 4.
The curve passes through the point (0, 2). The sum of the coordinates of any point on the curve exceeds the slope of the tangent to the curve at any point by 5. Find the equation of the curve.
Solution:
Let A(x, y) be any point on the curve.
Then slope of the tangent to the curve at the point A is \(\frac{d y}{d x}\).
According to the given condition
x + y = \(\frac{d y}{d x}\) + 5
∴ \(\frac{d y}{d x}\) – y = x – 5 ………(1)
This is the linear differential equation of the form
\(\frac{d y}{d x}\) + P . y = Q, where P = -1 and Q = x – 5
∴ I.F. = \(e^{\int P d x}=e^{\int-1 d x}=e^{-x}\)
∴ the solution of (1) is given by

This is the general equation of the curve.
But the required curve is passing through the point (0, 2).
∴ by putting x = 0, y = 2 in (2), we get
2 = 4 – 0 + c
∴ c = -2
∴ from (2), the equation of the required curve is y = 4 – x – 2ex.
![]()
Question 5.
If the slope of the tangent to the curve at each of its point is equal to the sum of abscissa and the product of the abscissa and ordinate of the point. Also, the curve passes through the point (0, 1). Find the equation of the curve.
Solution:
Let A(x, y) be the point on the curve y = f(x).
Then slope of the tangent to the curve at the point A is \(\frac{d y}{d x}\).
According to the given condition
\(\frac{d y}{d x}\) = x + xy
∴ \(\frac{d y}{d x}\) – xy = x ……….. (1)
This is the linear differential equation of the form
\(\frac{d y}{d x}\) + Py = Q, where P = -x and Q = x
∴ I.F. = \(e^{\int P d x}=e^{\int-x d x}=e^{-\frac{x^{2}}{2}}\)
∴ the solution of (1) is given by
y . (I.F.) = ∫Q . (I.F.) dx + c

This is the general equation of the curve.
But the required curve is passing through the point (0, 1).
∴ by putting x = 0 and y = 1 in (2), we get
1 + 1 = c
∴ c = 2
∴ from (2), the equation of the required curve is 1 + y = \(2 e^{\frac{x^{2}}{2}}\).