Balbharti 12th Maharashtra State Board Maths Solutions Book Pdf Chapter 6 Differential Equations Ex 6.2 Questions and Answers.
Maharashtra State Board 12th Maths Solutions Chapter 6 Differential Equations Ex 6.2
Question 1.
Obtain the differential equation by eliminating the arbitrary constants from the following equations:
(i) x3 + y3 = 4ax
Solution:
x3 + y3 = 4ax ……..(1)
Differentiating both sides w.r.t. x, we get
3x2 + 3y2 \(\frac{d y}{d x}\) = 4a × 1
∴ 3x2 + 3y2 \(\frac{d y}{d x}\) = 4a
Substituting the value of 4a in (1), we get
x3 + y3 = (3x2 + 3y2 \(\frac{d y}{d x}\)) x
∴ x3 + y3 = 3x3 + 3xy2 \(\frac{d y}{d x}\)
∴ 2x3 + 3xy2 \(\frac{d y}{d x}\) – y3 = 0
This is the required D.E.
![]()
(ii) Ax2 + By2 = 1
Solution:
Ax2 + By2 = 1
Differentiating both sides w.r.t. x, we get
A × 2x + B × 2y \(\frac{d y}{d x}\) = 0
∴ Ax + By \(\frac{d y}{d x}\) = 0 ……..(1)
Differentiating again w.r.t. x, we get

Substituting the value of A in (1), we get

This is the required D.E.
Alternative Method:
Ax2 + By2 = 1 ……..(1)
Differentiating both sides w.r.t. x, we get
A × 2x + B × 2y \(\frac{d y}{d x}\) = 0
∴ Ax + By \(\frac{d y}{d x}\) = 0 ……….(2)
Differentiating again w.r.t. x, we get,
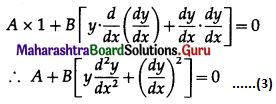
The equations (1), (2) and (3) are consistent in A and B.
∴ determinant of their consistency is zero.

This is the required D.E.
(iii) y = A cos(log x) + B sin(log x)
Solution:
y = A cos(log x) + B sin (log x) ……. (1)
Differentiating w.r.t. x, we get

(iv) y2 = (x + c)3
Solution:
y2 = (x + c)3
Differentiating w.r.t. x, we get

This is the required D.E.
![]()
(v) y = Ae5x + Be-5x
Solution:
y = Ae5x + Be-5x ……….(1)
Differentiating twice w.r.t. x, we get
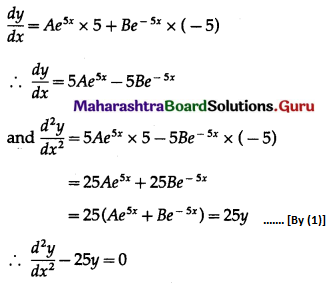
This is the required D.E.
(vi) (y – a)2 = 4(x – b)
Solution:
(y – a)2 = 4(x – b)
Differentiating both sides w.r.t. x, we get
2(y – a) . \(\frac{d}{d x}\)(y – a) = 4 \(\frac{d}{d x}\)(x – b)
∴ 2(y – a) . (\(\frac{d y}{d x}\) – 0) = 4(1 – 0)
∴ 2(y – a) \(\frac{d y}{d x}\) = 4
∴ (y – a) \(\frac{d y}{d x}\) = 2 ……..(1)
Differentiating w.r.t. x, we get

This is the required D.E.
(vii) y = a + \(\frac{a}{x}\)
Solution:
y = a + \(\frac{a}{x}\)
Differentiating w.r.t. x, we get

Substituting the value of a in (1), we get

This is the required D.E.
(viii) y = c1e2x + c2e5x
Solution:
y = c1e2x + c2e5x ………(1)
Differentiating twice w.r.t. x, we get
\(\frac{d y}{d x}\) = c1e2x × 2 + c2e5x × 5
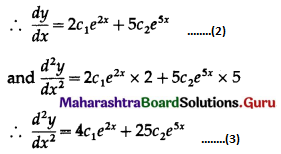
The equations (1), (2) and (3) are consistent in c1e2x and c2e5x
∴ determinant of their consistency is zero.

This is the required D.E.
![]()
Alternative Method:
y = c1e2x + c2e5x
Dividing both sides by e5x, we get

This is the required D.E.
(ix) c1x3 + c2y2 = 5.
Solution:
c1x3 + c2y2 = 5 ……….(1)
Differentiating w.r.t. x, we get
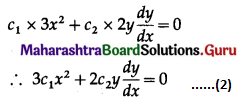
Differentiating again w.r.t. x, we get

The equations (1), (2) and (3) in c1, c2 are consistent.
∴ determinant of their consistency is zero.

This is the required D.E.
![]()
(x) y = e-2x(A cos x + B sin x)
Solution:
y = e-2x(A cos x + B sin x)
∴ e2x . y = A cos x + B sin x ………(1)
Differentiating w.r.t. x, we get
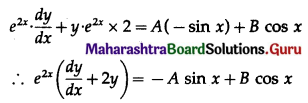
Differentiating again w.r.t. x, we get
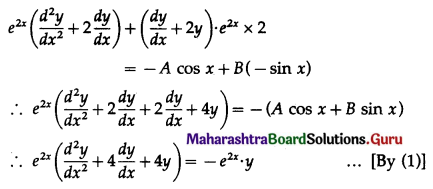
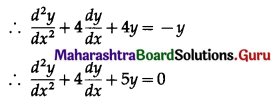
This is the required D.E.
Question 2.
Form the differential equation of family of lines having intercepts a and b on the coordinate axes respectively.
Solution:
The equation of the line having intercepts a and b on the coordinate axes respectively, is
\(\frac{x}{a}+\frac{y}{b}=1\) ……….(1)
where a and b are arbitrary constants.
[For different values of a and b, we get, different lines. Hence (1) is the equation of family of lines.]
Differentiating (1) w.r.t. x, we get
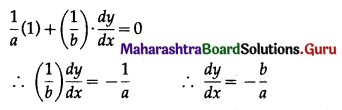
Differentiating again w.r.t. x, we get \(\frac{d^{2} y}{d x^{2}}=0\)
This is the required D.E.
![]()
Question 3.
Find the differential equation all parabolas having length of latus rectum 4a and axis is parallel to the X-axis.
Solution:
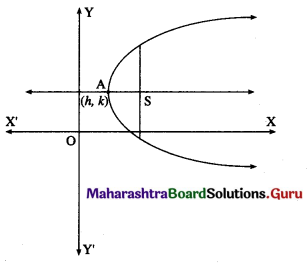
Let A(h, k) be the vertex of the parabola whose length of latus rectum is 4a.
Then the equation of the parabola is (y – k)2 = 4a (x – h), where h and k are arbitrary constants.
Differentiating w.r.t. x, we get

Differentiating again w.r.t. x, we get

This is the required D.E.
Question 4.
Find the differential equation of the ellipse whose major axis is twice its minor axis.
Solution:
Let 2a and 2b be lengths of major axis and minor axis of the ellipse.
Then 2a = 2(2b)
∴ a = 2b
∴ equation of the ellipse is
\(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1\)
i.e., \(\frac{x^{2}}{(2 b)^{2}}+\frac{y^{2}}{b^{2}}=1\)
∴ \(\frac{x^{2}}{4 b^{2}}+\frac{y^{2}}{b^{2}}=1\)
∴ x2 + 4y2 = 4b2
Differentiating w.r.t. x, we get
2x + 4 × 2y \(\frac{d y}{d x}\) = 0
∴ x + 4y \(\frac{d y}{d x}\) = 0
This is the required D.E.
![]()
Question 5.
Form the differential equation of family of lines parallel to the line 2x + 3y + 4 = 0.
Solution:
The equation of the line parallel to the line 2x + 3y + 4 = 0 is 2x + 3y + c = 0, where c is an arbitrary constant.
Differentiating w.r.t. x, we get
2 × 1 + 3 \(\frac{d y}{d x}\) + 0 = 0
∴ 3 \(\frac{d y}{d x}\) + 2 = 0
This is the required D.E.
Question 6.
Find the differential equation of all circles having radius 9 and centre at point (h, k).
Solution:
Equation of the circle having radius 9 and centre at point (h, k) is
(x – h)2 + (y – k)2 = 81 …… (1)
where h and k are arbitrary constant.
Differentiating (1) w.r.t. x, we get

Differentiating again w.r.t. x, we get

From (2), x – h = -(y – k) \(\frac{d y}{d x}\)
Substituting the value of (x – h) in (1), we get
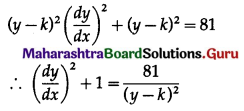

This is the required D.E.
![]()
Question 7.
Form the differential equation of all parabolas whose axis is the X-axis.
Solution:
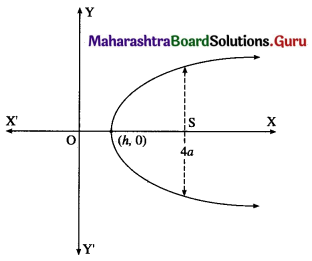
The equation of the parbola whose axis is the X-axis is
y2 = 4a(x – h) …… (1)
where a and h are arbitrary constants.
Differentiating (1) w.r.t. x, we get
2y \(\frac{d y}{d x}\) = 4a(1 – 0)
∴ y \(\frac{d y}{d x}\) = 2a
Differentiating again w.r.t. x, we get
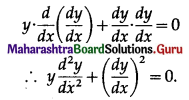
This is the required D.E.