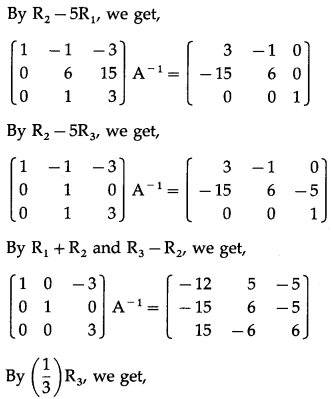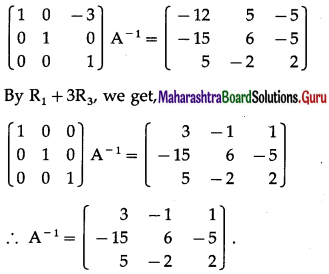Balbharti 12th Maharashtra State Board Maths Solutions Book Pdf Chapter 2 Matrices Ex 2.2 Questions and Answers.
Maharashtra State Board 12th Maths Solutions Chapter 2 Matrices Ex 2.2
Question 1.
Find the co-factors of the elements of the following matrices
(i) \(\left[\begin{array}{cc}
-1 & 2 \\
-3 & 4
\end{array}\right]\)
Solution:
Let A = \(\left[\begin{array}{cc}
-1 & 2 \\
-3 & 4
\end{array}\right]\)
Here, a11 = -11, M11 = 4
∴ A11 = (-1)1+1(4) = 4
a12 = 2, M12 = -3
∴ A12 = (-1)1+2(- 3) = 3
a21 = – 3, M21 = -2
∴ A21 = (- 1)2+1(2) = -2
a22 = 4, M22 = -1
∴ A22 = (-1)2+2(-1) = -1.
(ii) \(\left[\begin{array}{ccc}
1 & -1 & 2 \\
-2 & 3 & 5 \\
-2 & 0 & -1
\end{array}\right]\)
Solution:
Let A = \(\left[\begin{array}{ccc}
1 & -1 & 2 \\
-2 & 3 & 5 \\
-2 & 0 & -1
\end{array}\right]\)
The co-factor of aij is given by Aij = (-1)i+jMij

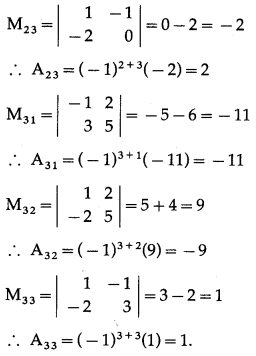
![]()
Question 2.
Find the matrix of co-factors for the following matrices
(i) \(\left[\begin{array}{rr}
1 & 3 \\
4 & -1
\end{array}\right]\)
Solution:
Let A = \(\left[\begin{array}{rr}
1 & 3 \\
4 & -1
\end{array}\right]\)
Here, a11 = 1, M11 = -1
∴ A11 = (-1)1+1(-1) = -1
a12 = 3, M12 = 4
∴ A12 = (-1)1+2(4) = -4
a21 = 4, M21 = 3
∴ A21 = (-1)2+1(3) = -3
a22 = -1, M22 = 1
∴ A22 = (-1)2+1(1) = 1
∴ the co-factor matrix = \(\left[\begin{array}{ll}
A_{11} & A_{12} \\
A_{21} & A_{22}
\end{array}\right]\)
= \(\left(\begin{array}{rr}
-1 & -4 \\
-3 & 1
\end{array}\right)\)
(ii) \(\left[\begin{array}{rrr}
1 & 0 & 2 \\
-2 & 1 & 3 \\
0 & 3 & -5
\end{array}\right]\)
Solution:
Let A = \(\left[\begin{array}{rrr}
1 & 0 & 2 \\
-2 & 1 & 3 \\
0 & 3 & -5
\end{array}\right]\)
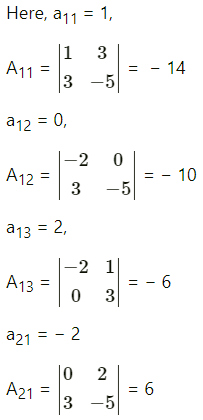
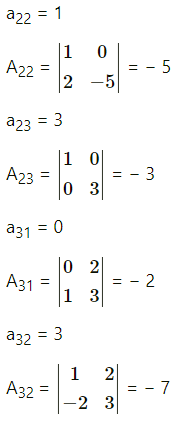
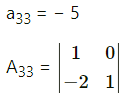
A11 = -14, A12 = -10, A13 = -6,
A21 = 6, A22 = -5, A23 = -3,
A31 = -2, A32 = -7, A33 = 1.
∴ the co-factor matrix
= \(\left[\begin{array}{lll}
A_{11} & A_{12} & A_{13} \\
A_{21} & A_{22} & A_{23} \\
A_{31} & A_{32} & A_{33}
\end{array}\right]\) = \(\left[\begin{array}{rrr}
-14 & -10 & -6 \\
6 & -5 & -3 \\
-2 & -7 & 1
\end{array}\right]\)
![]()
Question 3.
Find the adjoint of the following matrices.
(i) \(\left[\begin{array}{cc}
2 & -3 \\
3 & 5
\end{array}\right]\)
Solution:
Let A = \(\left[\begin{array}{cc}
2 & -3 \\
3 & 5
\end{array}\right]\)
Here, a11 = 2, M11= 5
∴ A11 = (-1)1+1(5) = 5
a12 = -3, M12 = 3
∴ A12 = (-1)1+2(3) = -3
a21 = 3, M21 = -3
∴ A A21 = (-1)2+1(-3) = 3
a22 = 5, M22 = 2
∴ A22 = (-1)2+1 = 2
∴ the co-factor matrix = \(\left[\begin{array}{ll}
A_{11} & A_{12} \\
A_{21} & A_{22}
\end{array}\right]\)
= \(\left[\begin{array}{rr}
5 & -3 \\
3 & 2
\end{array}\right]\)
∴ adj A = \(\left(\begin{array}{rr}
5 & 3 \\
-3 & 2
\end{array}\right)\)
![]()
(ii) \(\left[\begin{array}{ccc}
1 & -1 & 2 \\
-2 & 3 & 5 \\
-2 & 0 & -1
\end{array}\right]\)
Solution:

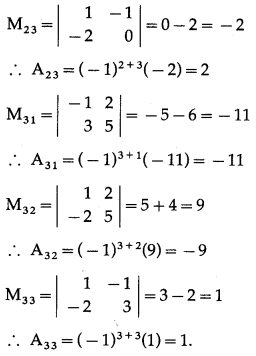
A11 = -3, A12 = -12, A13 = 6,
A21 = -1, A22 = 3, A23 = 2,
A31 = -11, A32 = -9, A33 = 1
∴ the co-factor matrix = \(\left[\begin{array}{lll}
\mathrm{A}_{11} & \mathrm{~A}_{12} & \mathrm{~A}_{15} \\
\mathrm{~A}_{21} & \mathrm{~A}_{22} & \mathrm{~A}_{23} \\
\mathrm{~A}_{31} & \mathrm{~A}_{32} & \mathrm{~A}_{33}
\end{array}\right]\)
= \(\left[\begin{array}{rrr}
-3 & -12 & 6 \\
-1 & 3 & 2 \\
-11 & -9 & 1
\end{array}\right]\)
∴ adj A = \(\left[\begin{array}{rrr}
-3 & -1 & -11 \\
-12 & 3 & -9 \\
6 & 2 & 1
\end{array}\right]\)
Question 4.
If A = \(\left[\begin{array}{ccc}
1 & -1 & 2 \\
3 & 0 & -2 \\
1 & 0 & 3
\end{array}\right]\), verify that A (adj A) = (adj A) A = | A | ∙ I
Solution:
A = \(\left[\begin{array}{ccc}
1 & -1 & 2 \\
3 & 0 & -2 \\
1 & 0 & 3
\end{array}\right]\)
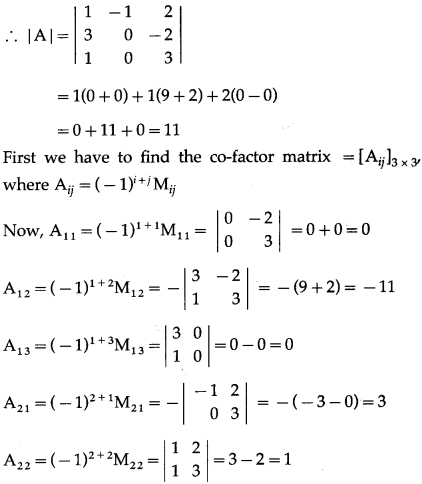



From (1), (2) and (3), we get,
A(adj A) = (adj A)A = |A|∙I.
Note: This relation is valid for any non-singular matrix A.
![]()
Question 5.
Find the inverse of the following matrices by the adjoint method
(i) \(\left[\begin{array}{ll}
-1 & 5 \\
-3 & 2
\end{array}\right]\)
Solution:
Let A = \(\left[\begin{array}{ll}
-1 & 5 \\
-3 & 2
\end{array}\right]\)
∴ |A| = \(\left|\begin{array}{ll}
-1 & 5 \\
-3 & 2
\end{array}\right|\) = -2 + 15 = 13 ≠ 0
∴ A-1 exists.
First we have to find the co-factor matrix
= [Aij]2×2, where Aij = (-1)i+jMij
Now, A11 = (-1)1+1M11 = 2
A12 = (-1)1+2M12 = -(-3) = 3
A21 = (-1)2+1M21 = -5
A22 = (-1)2+2M22 = -1
Hence, the co-factor matrix
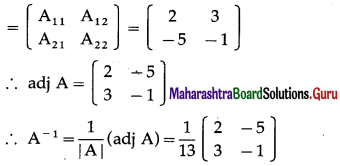
(ii) \(\left[\begin{array}{cc}
2 & -2 \\
4 & 3
\end{array}\right]\)
Solution:
Let A = \(\left[\begin{array}{cc}
2 & -2 \\
4 & 3
\end{array}\right]\)
|A| = \(\) = 6 + 8 = 14 ≠ 0
∴ A-1 exist
First we have to find the co-factor matrix
= [Aij] 2×2 where Aij = (-1)i+jMij
Now, A11 = (-1)1+1M11 = 3
A12 = (-1)1+2M = -4
A21 = (-2)2+1M21 = (-2) = 2
A22 = (-1)2+2M22 = 2
Hence the co-factor matrix
= \(\left[\begin{array}{ll}
A_{11} & A_{12} \\
A_{21} & A_{22}
\end{array}\right]\) = \(\left[\begin{array}{cc}
3 & -4 \\
2 & 2
\end{array}\right]\)
∴ adj A = \(\left[\begin{array}{cc}
3 & 2 \\
-4 & 2
\end{array}\right]\)
∴ A-1 = \(\frac{1}{|\mathrm{~A}|}\) (adj A) = \(\frac{1}{14}\left(\begin{array}{cc}
3 & 2 \\
-4 & 2
\end{array}\right)\)
![]()
(iii) \(\left[\begin{array}{ccc}
1 & 0 & 0 \\
3 & 3 & 0 \\
5 & 2 & -1
\end{array}\right]\)
Solution:
Let A = \(\left[\begin{array}{ccc}
1 & 0 & 0 \\
3 & 3 & 0 \\
5 & 2 & -1
\end{array}\right]\)
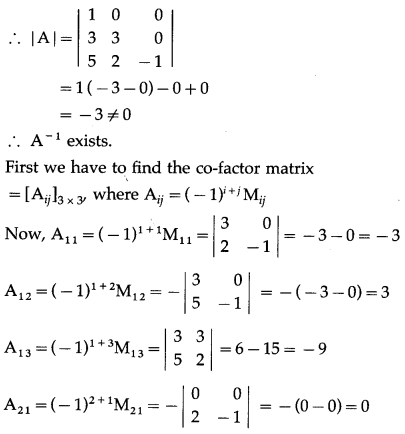

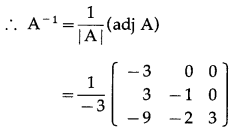
∴ A-1 = \(\frac{1}{3}\left[\begin{array}{rrr}
3 & 0 & 0 \\
-3 & 1 & 0 \\
9 & 2 & -3
\end{array}\right]\)
(iv) \(\left[\begin{array}{lll}
1 & 2 & 3 \\
0 & 2 & 4 \\
0 & 0 & 5
\end{array}\right]\)
Solution:
Let A = \(\left[\begin{array}{lll}
1 & 2 & 3 \\
0 & 2 & 4 \\
0 & 0 & 5
\end{array}\right]\)
∴ |A| = \(\left[\begin{array}{lll}
1 & 2 & 3 \\
0 & 2 & 4 \\
0 & 0 & 5
\end{array}\right]\)
= 1(10 – 0) – 0 + 0
= 1(10) – 0 + 0
= 10 ≠ 0
∴ A-1 exists.
First we have to find the co-factor matrix
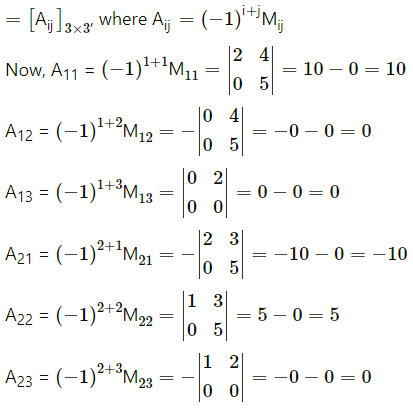
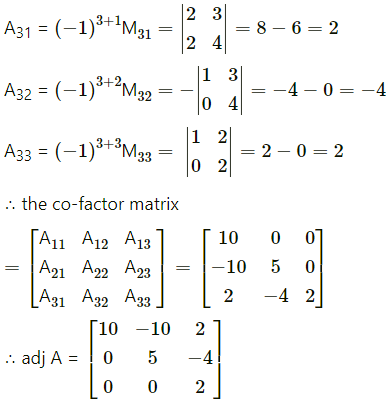
∴ A-1 = \(\frac{1}{|\mathrm{~A}|}\) (adj A)
= \(\frac{1}{10}\left(\begin{array}{rrr}
10 & -10 & 2 \\
0 & 5 & -4 \\
0 & 0 & 2
\end{array}\right)\)
∴ A-1 = \(\frac{1}{10}\left(\begin{array}{rrr}
10 & -10 & 2 \\
0 & 5 & -4 \\
0 & 0 & 2
\end{array}\right)\)
![]()
Question 6.
Find the inverse of the following matrices
(i) \(\left[\begin{array}{cc}
1 & 2 \\
2 & -1
\end{array}\right]\)
Solution:
Let A = \(\left[\begin{array}{cc}
1 & 2 \\
2 & -1
\end{array}\right]\)

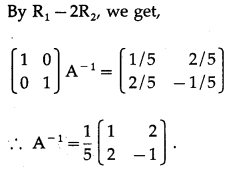

(ii) \(\left[\begin{array}{cc}
2 & -3 \\
-1 & 2
\end{array}\right]\)
Solution:
Let A = \(\left[\begin{array}{cc}
2 & -3 \\
-1 & 2
\end{array}\right]\)
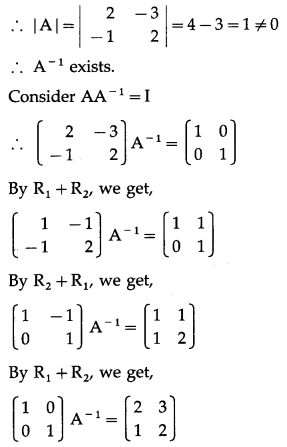
∴ A-1 = \(\left(\begin{array}{ll}
2 & 3 \\
1 & 2
\end{array}\right)\)
![]()
(iii) \(\left[\begin{array}{lll}
0 & 1 & 2 \\
1 & 2 & 3 \\
3 & 1 & 1
\end{array}\right]\)
Solution:
Let A = \(\left[\begin{array}{lll}
0 & 1 & 2 \\
1 & 2 & 3 \\
3 & 1 & 1
\end{array}\right]\)
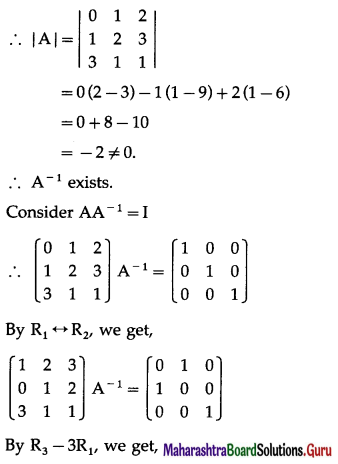
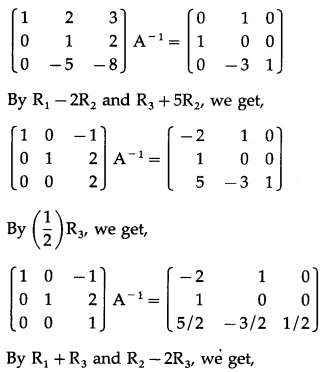
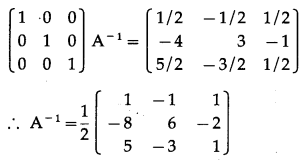
(iv) \(\left[\begin{array}{ccc}
2 & 0 & -1 \\
5 & 1 & 0 \\
0 & 1 & 3
\end{array}\right]\)
Solution:
Let A = \(\left[\begin{array}{ccc}
2 & 0 & -1 \\
5 & 1 & 0 \\
0 & 1 & 3
\end{array}\right]\)