Balbharti 12th Maharashtra State Board Maths Solutions Book Pdf Chapter 1 Differentiation Ex 1.3 Questions and Answers.
Maharashtra State Board 12th Maths Solutions Chapter 1 Differentiation Ex 1.3
Question 1.
Differentiate the following w.r.t. x:
(i) \(\frac{(x+1)^{2}}{(x+2)^{3}(x+3)^{4}}\)
Solution:
Let y = \(\frac{(x+1)^{2}}{(x+2)^{3}(x+3)^{4}}\)
Then, log y = log [latex]\frac{(x+1)^{2}}{(x+2)^{3}(x+3)^{4}}[/latex]
= log (x + 1)2 – log (x + 2)3 – log (x + 3)4
= 2 log (x +1) – 3 log (x + 2) – 4 log (x + 3)
Differentiating both sides w.r.t. x, we get

(ii) \(\sqrt[3]{\frac{4 x-1}{(2 x+3)(5-2 x)^{2}}}\)
Solution:
Let y = \(\sqrt[3]{\frac{4 x-1}{(2 x+3)(5-2 x)^{2}}}\)
Then log y = log [latex]\sqrt[3]{\frac{4 x-1}{(2 x+3)(5-2 x)^{2}}}[/latex]

Differentiating both sides w.r.t. x, we get

![]()
(iii) \(\left(x^{2}+3\right)^{\frac{3}{2}} \cdot \sin ^{3} 2 x \cdot 2^{x^{2}}\)
Solution:
Let y = \(\left(x^{2}+3\right)^{\frac{3}{2}} \cdot \sin ^{3} 2 x \cdot 2^{x^{2}}\)
Then log y = log [latex]\left(x^{2}+3\right)^{\frac{3}{2}} \cdot \sin ^{3} 2 x \cdot 2^{x^{2}}[/latex]
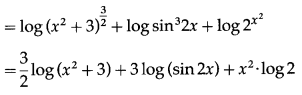
Differentiating both sides w.r.t. x, we get

(iv) \(\frac{\left(x^{2}+2 x+2\right)^{\frac{3}{2}}}{(\sqrt{x}+3)^{3}(\cos x)^{x}}\)
Solution:
Let y = \(\frac{\left(x^{2}+2 x+2\right)^{\frac{3}{2}}}{(\sqrt{x}+3)^{3}(\cos x)^{x}}\)
Then log y = log [latex]\frac{\left(x^{2}+2 x+2\right)^{\frac{3}{2}}}{(\sqrt{x}+3)^{3}(\cos x)^{x}}[/latex]
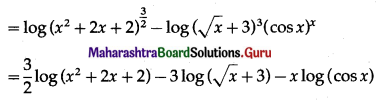
Differentiating both sides w.r.t. x, we get

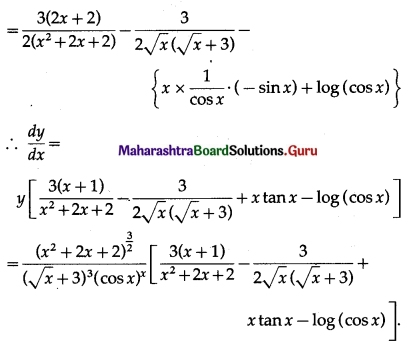
(v) \(\frac{x^{5} \cdot \tan ^{3} 4 x}{\sin ^{2} 3 x}\)
Solution:
Let y = \(\frac{x^{5} \cdot \tan ^{3} 4 x}{\sin ^{2} 3 x}\)
Then log y = log [latex]\frac{x^{5} \cdot \tan ^{3} 4 x}{\sin ^{2} 3 x}[/latex]
= log x5 + log tan34x – log sin23x
= 5 log x+ 3 log (tan 4x) – 2 log (sin 3x)
Differentiating both sides w.r.t. x, we get

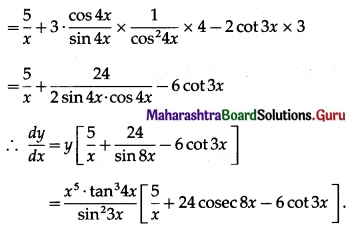
(vi) \(x^{\tan ^{-1} x}\)
Solution:
Let y = \(x^{\tan ^{-1} x}\)
Then log y = log (\(x^{\tan ^{-1} x}\)) = (tan-1 x)(log x)
Differentiating both sides w.r.t. x, we get
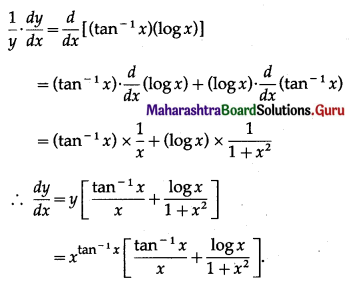
(vii) (sin x)x
Solution:
Let y = (sin x)x
Then log y = log (sin x)x = x . log (sin x)
Differentiating both sides w.r.t. x, we get
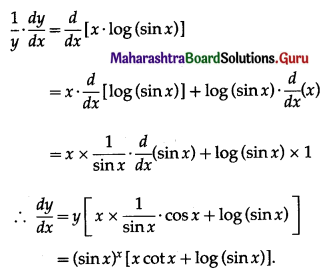
(viii) sin xx
Solution:
Let y = (sin xx)
Then \(\frac{d y}{d x}=\frac{d}{d x}\left[\left(\sin x^{x}\right)\right]\)
\(\frac{d y}{d x}=\cos \left(x^{x}\right) \cdot \frac{d}{d x}\left(x^{x}\right)\) ……. (1)
Let u = xx
Then log u = log xx = x . log x
Differentiating both sides w.r.t. x, we get

![]()
Question 2.
Differentiate the following w.r.t. x:
(i) xe + xx + ex + ee
Solution:
Let y = xe + xx + ex + ee
Let u = xx
Then log u = log xx = x log x
Differentiating both sides w.r.t. x, we get
\(\frac{1}{u} \cdot \frac{d u}{d x}=\frac{d}{d x}(x \log x)\)

(ii) \(x^{x^{x}}+e^{x^{x}}\)
Solution:
Let y = \(x^{x^{x}}+e^{x^{x}}\)
Put u = \(x^{x^{x}}\) and v = \(e^{x^{x}}\)
Then y = u + v
∴ \(\frac{d y}{d x}=\frac{d u}{d x}+\frac{d v}{d x}\)
Take u = \(x^{x^{x}}\)
log u = log \(x^{x^{x}}\) = xx . log x
Differentiating both sides w.r.t. x, we get



(iii) (log x)x – (cos x)cot x
Solution:
Let y = (log x)x – (cos x)cot x
Put u = (log x)x and v = (cos x)cot x
Then y = u – v
∴ \(\frac{d y}{d x}=\frac{d u}{d x}-\frac{d v}{d x}\) ……..(1)
Take u = (log x)x
∴ log u = log (log x)x = x . log (log x)
Differentiating both sides w.r.t. x, we get


(iv) \(x^{e^{x}}+(\log x)^{\sin x}\)
Solution:
Let y = \(x^{e^{x}}+(\log x)^{\sin x}\)
Put u = \(x^{e^{x}}\) and v = (log x)sin x
Then y = u + v
∴ \(\frac{d y}{d x}=\frac{d u}{d x}+\frac{d v}{d x}\) ……….(1)
Take u = \(x^{e^{x}}\)
∴ log u = log \(x^{e^{x}}\) = ex . log x
Differentiating both sides w.r.t. x, we get

Also, v = (log x)sin x
∴ log v = log (log x)sin x = (sin x) . (log log x)
Differentiating both sides w.r.t. x, we get
\(\frac{1}{v} \cdot \frac{d v}{d x}=\frac{d}{d x}[(\sin x) \cdot(\log \log x)]\)
= \((\sin x) \cdot \frac{d}{d x}\left[(\log \log x)+(\log \log x) \cdot \frac{d}{d x}(\sin x)\right]\)
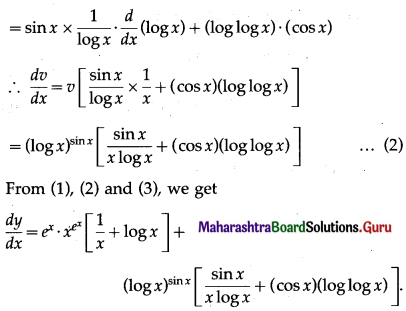
![]()
(v) \(e^{\tan x}+(\log x)^{\tan x}\)
Solution:
Let y = \(e^{\tan x}+(\log x)^{\tan x}\)
Put u = (log x)tan x
∴ log u =log(log x)tan x = (tan x).(log log x)
Differentiating both sides w.r.t. x, we get

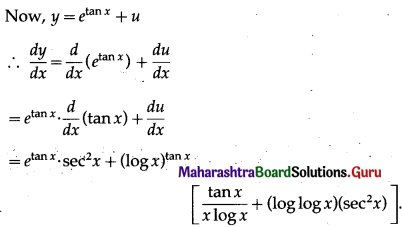
(vi) (sin x)tan x + (cos x)cot x
Solution:
Let y = (sin x)tan x + (cos x)cot x
Put u = (sin x)tan x and v = (cos x)cot x
Then y = u + v
∴ \(\frac{d y}{d x}=\frac{d u}{d x}+\frac{d v}{d x}\) ………(1)
Take u = (sin x)tan x
∴ log u = log (sin x)tan x = (tan x) . (log sin x)
Differentiating both sides w.r.t. x, we get

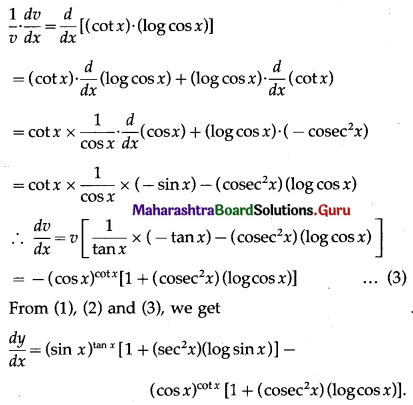
(vii) \(10^{x^{x}}+x^{x^{10}}+x^{10^{x}}\)
Solution:
Let y = \(10^{x^{x}}+x^{x^{10}}+x^{10^{x}}\)
Put u = \(10^{x^{x}}\), v = \(x^{x^{10}}\) and w = \(x^{10^{x}}\)
Then y = u + v + w
∴ \(\frac{d y}{d x}=\frac{d u}{d x}+\frac{d v}{d x}+\frac{d w}{d x}\) ………(1)




(viii) \(\left[(\tan x)^{\tan x}\right]^{\tan x}\) at x = \(\frac{\pi}{4}\)
Solution:
Let y = \(\left[(\tan x)^{\tan x}\right]^{\tan x}\)
∴ log y = log [latex]\left[(\tan x)^{\tan x}\right]^{\tan x}[/latex]
= tan x . log(tan x)tan x
= tan x . tan x log (tan x)
= (tan x)2 . log (tan x)
Differentiating both sides w.r.t. x, we get

Question 3.
Find \(\frac{d y}{d x}\) if
(i) √x + √y = √a
Solution:
√x + √y = √a
Differentiating both sides w.r.t. x, we get
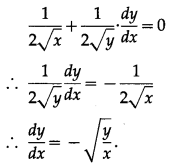
(ii) x√x + y√y = a√a
Solution:
x√x + y√y = a√a
∴ \(x^{\frac{3}{2}}+y^{\frac{3}{2}}=a^{\frac{3}{2}}\)
Differentiating both sides w.r.t. x, we get
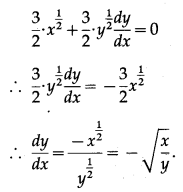
(iii) x + √xy + y = 1
Solution:
x + √xy + y = 1
Differentiating both sides w.r.t. x, we get
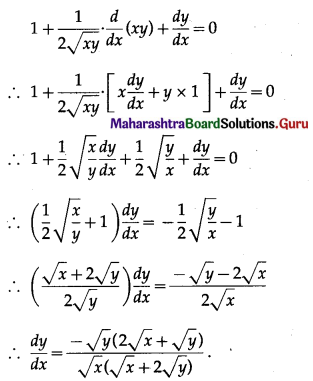
![]()
(iv) x3 + x2y + xy2 + y3 = 81
Solution:
x3 + x2y + xy2 + y3 = 81
Differentiating both sides w.r.t. x, we get
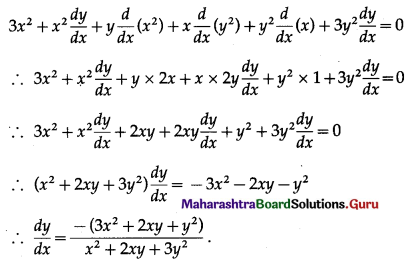
(v) x2y2 – tan-1(\(\sqrt{x^{2}+y^{2}}\)) = cot-1(\(\sqrt{x^{2}+y^{2}}\))
Solution:
x2y2 – tan-1(\(\sqrt{x^{2}+y^{2}}\)) = cot-1(\(\sqrt{x^{2}+y^{2}}\))
∴ x2y2 = tan-1(\(\sqrt{x^{2}+y^{2}}\)) + cot-1(\(\sqrt{x^{2}+y^{2}}\))
∴ x2y2 = \(\frac{\pi}{2}\) …….[∵ \(\tan ^{-1} x+\cot ^{-1} x=\frac{\pi}{2}\)]
Differentiating both sides w.r.t. x, we get

(vi) xey + yex = 1
Solution:
xey + yex = 1
Differentiating both sides w.r.t. x, we get
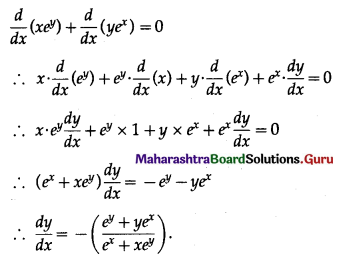
(vii) ex+y = cos (x – y)
Solution:
ex+y = cos (x – y)
Differentiating both sides w.r.t. x, we get
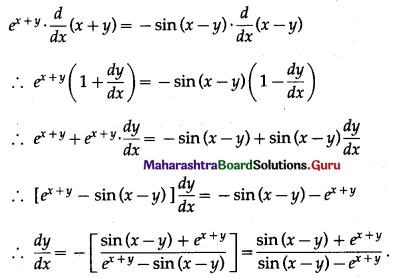
(viii) cos (xy) = x + y
Solution:
cos (xy) = x + y
Differentiating both sides w.r.t. x, we get
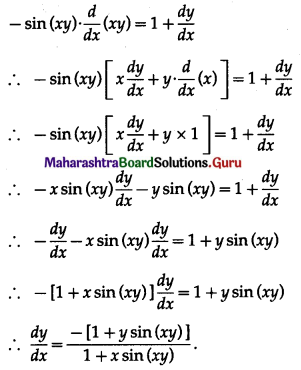
(ix) \(e^{e^{x-y}}=\frac{x}{y}\)
Solution:
\(e^{e^{x-y}}=\frac{x}{y}\)
∴ ex-y = log(\(\frac{x}{y}\)) …….[ex = y ⇒ x = log y]
∴ ex-y = log x – log y
Differentiating both sides w.r.t. x, we get

Question 4.
Show that \(\frac{d y}{d x}=\frac{y}{x}\) in the following, where a and p are constants.
(i) x7y5 = (x + y)12
Solution:
x7y5 = (x + y)12
(log x7y5) = log(x + y)12
log x7 + log y5 = log(x + y)12
7 log x + 5 log y = 12 log (x + y)
Differentiating both sides w.r.t. x, we get

![]()
(ii) xpy4 = (x + y)p+4, p∈N
Solution:
xpy4 = (x + y)p+4
Taking log
log (xpy4) = log(x + y)p+4
log xp + log y4 = (p + 4) log(x + y)
p log x + 4 log y = (p + 4) log(x + y)
Differentiating both sides w.r.t. x, we get
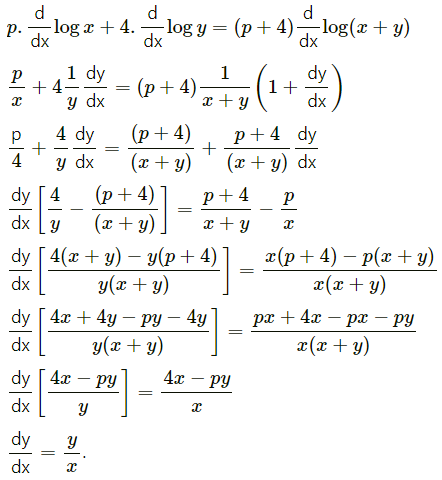
(iii) \(\sec \left(\frac{x^{5}+y^{5}}{x^{5}-y^{5}}\right)=a^{2}\)
Solution:
\(\sec \left(\frac{x^{5}+y^{5}}{x^{5}-y^{5}}\right)=a^{2}\)

Differentiating both sides w.r.t. x, we get


Differentiating both sides w.r.t. x, we get

(iv) \(\tan ^{-1}\left(\frac{3 x^{2}-4 y^{2}}{3 x^{2}+4 y^{2}}\right)=a^{2}\)
Solution:
\(\tan ^{-1}\left(\frac{3 x^{2}-4 y^{2}}{3 x^{2}+4 y^{2}}\right)=a^{2}\)
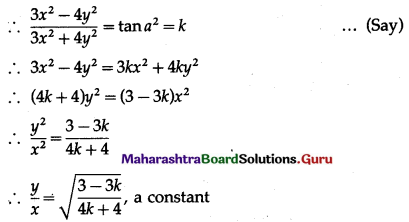
Differentiating both sides w.r.t. x, we get

(v) \(\cos ^{-1}\left(\frac{7 x^{4}+5 y^{4}}{7 x^{4}-5 y^{4}}\right)=\tan ^{-1} a\)
Solution:
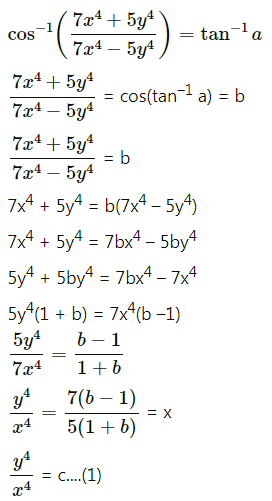
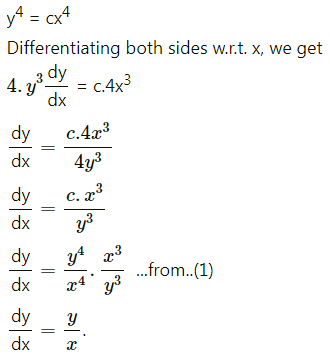
(vi) \(\log \left(\frac{x^{20}-y^{20}}{x^{20}+y^{20}}\right)=20\)
Solution:
\(\log \left(\frac{x^{20}-y^{20}}{x^{20}+y^{20}}\right)=20\)

Differentiating both sides w.r.t. x, we get

![]()
(vii) \(e^{\frac{x^{7}-y^{7}}{x^{7}+y^{7}}}=a\)
Solution:
\(e^{\frac{x^{7}-y^{7}}{x^{7}+y^{7}}}=a\)

Differentiating both sides w.r.t. x, we get

(viii) \(\sin \left(\frac{x^{3}-y^{3}}{x^{3}+y^{3}}\right)=a^{3}\)
Solution:
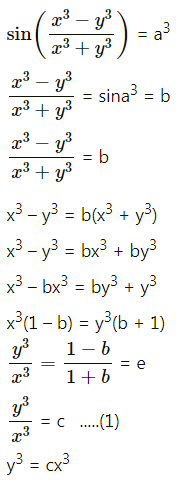
Differentiating both sides w.r.t. x, we get
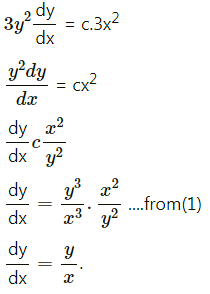
Question 5.
(i) If log (x + y) = log (xy) + p, where p is a constant, then prove that \(\frac{d y}{d x}=-\frac{y^{2}}{x^{2}}\).
Solution:
log (x + y) = log (xy) + p
∴ log (x + y) = log x + log y + p
Differentiating both sides w.r.t. x, we get

(ii) If \(\log _{10}\left(\frac{x^{3}-y^{3}}{x^{3}+y^{3}}\right)=2\), show that \(\frac{d y}{d x}=-\frac{99 x^{2}}{101 y^{2}}\)
Solution:
\(\log _{10}\left(\frac{x^{3}-y^{3}}{x^{3}+y^{3}}\right)=2\)

(iii) If \(\log _{5}\left(\frac{x^{4}+y^{4}}{x^{4}-y^{4}}\right)=2\), show that \(\frac{d y}{d x}=-\frac{12 x^{3}}{13 y^{3}}\)
Solution:
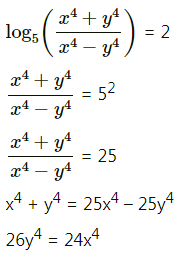
Differentiating both sides w.r.t. x, we get
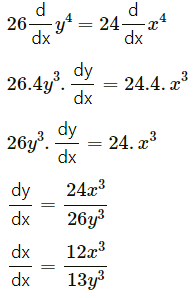
(iv) If ex + ey = ex+y, then show that \(\frac{d y}{d x}=-e^{y-x}\)
Solution:
ex + ey = ex+y ……(1)
Differentiating both sides w.r.t. x, we get

![]()
(v) If \(\sin ^{-1}\left(\frac{x^{5}-y^{5}}{x^{5}+y^{5}}\right)=\frac{\pi}{6}\), show that \(\frac{d y}{d x}=\frac{x^{4}}{3 y^{4}}\)
Solution:
\(\sin ^{-1}\left(\frac{x^{5}-y^{5}}{x^{5}+y^{5}}\right)=\frac{\pi}{6}\)
\(\frac{x^{5}-y^{5}}{x^{5}+y^{5}}=\sin \frac{\pi}{6}=\frac{1}{2}\)
2x5 – 2y5 = x5 + y5
3y5 = x5
Differentiating both sides w.r.t. x, we get
\(3 \times 5 y^{4} \frac{d y}{d x}=5 x^{4}\)
∴ \(\frac{d y}{d x}=\frac{x^{4}}{3 y^{4}}\)
(vi) If xy = ex-y, then show that \(\frac{d y}{d x}=\frac{\log x}{(1+\log x)^{2}}\)
Solution:
xy = ex-y
log xy = log ex-y
y log x = (x – y) log e
y log x = (x – y) ….. [∵ log e = 1]
y + y log x = x – y
y + y log x = x
y(1 + log x) = x
y = \(\frac{x}{1+\log x}\)
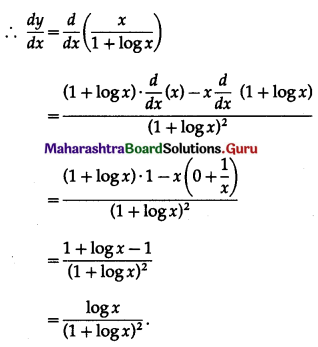
(vii) If \(y=\sqrt{\cos x+\sqrt{\cos x+\sqrt{\cos x+\ldots \infty}}}\), then show that \(\frac{d y}{d x}=\frac{\sin x}{1-2 y}\)
Solution:
\(y=\sqrt{\cos x+\sqrt{\cos x+\sqrt{\cos x+\ldots \infty}}}\)
y2 = cos x + \(\sqrt{\cos x+\sqrt{\cos x+\ldots \infty}}\)
y2 = cos x + y
Differentiating both sides w.r.t. x, we get
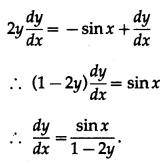
(viii) If \(y=\sqrt{\log x+\sqrt{\log x+\sqrt{\log x+\ldots \infty}}}\), then show that \(\frac{d y}{d x}=\frac{1}{x(2 y-1)}\)
Solution:
\(y=\sqrt{\log x+\sqrt{\log x+\sqrt{\log x+\ldots \infty}}}\)
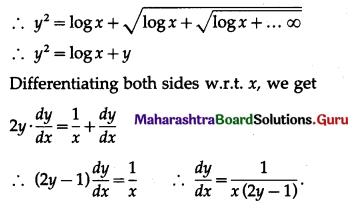
(ix) If \(y=x^{x^{x^{-\infty}}}\), then show that \(\frac{d y}{d x}=\frac{y^{2}}{x(1-\log y)}\)
Solution:
\(y=x^{x^{x^{-\infty}}}\)
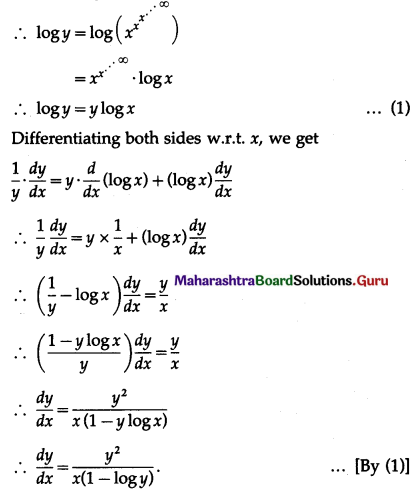
![]()
(x) If ey = yx, then show that \(\frac{d y}{d x}=\frac{(\log y)^{2}}{\log y-1}\)
Solution:
ey = yx
log ey = log yx
y log e = x log y
y = x log y …… [∵log e = 1] ……….(1)
Differentiating both sides w.r.t. x, we get
\(\frac{d y}{d x}=x \frac{d}{d x}(\log y)+(\log y) \cdot \frac{d}{d x}(x)\)

