Balbharti Maharashtra State Board 11th Maths Book Solutions Pdf Chapter 9 Differentiation Ex 9.2 Questions and Answers.
Maharashtra State Board 11th Maths Solutions Chapter 9 Differentiation Ex 9.2
(I) Differentiate the following w.r.t. x
Question 1.
y = \(x^{\frac{4}{3}}+e^{x}-\sin x\)
Solution:
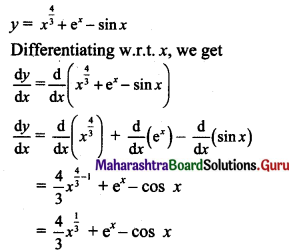
Question 2.
y = √x + tan x – x3
Solution:
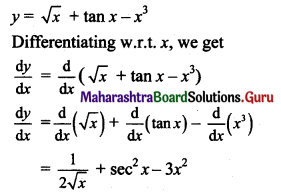
Question 3.
y = log x – cosec x + \(5^{x}-\frac{3}{x^{\frac{3}{2}}}\)
Solution:

![]()
Question 4.
y = \(x^{\frac{7}{3}}+5 x^{\frac{4}{5}}-\frac{5}{x^{\frac{2}{5}}}\)
Solution:

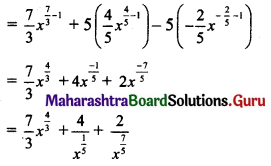
Question 5.
y = 7x + x7 – \(\frac{2}{3}\) x√x – log x + 77
Solution:

Question 6.
y = 3 cot x – 5ex + 3 log x – \(\frac{4}{x^{\frac{3}{4}}}\)
Solution:

(II) Diffrentiate the following w.r.t. x
Question 1.
y = x5 tan x
Solution:

Question 2.
y = x3 log x
Solution:
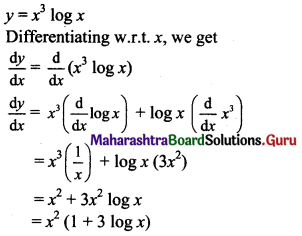
![]()
Question 3.
y = (x2 + 2)2 sin x
Solution:
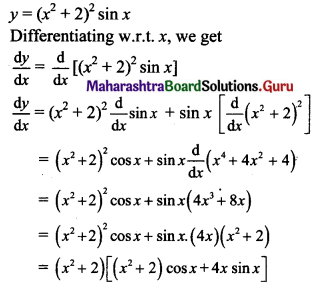
Question 4.
y = ex log x
Solution:

Question 5.
y = \(x^{\frac{3}{2}} e^{x} \log x\)
Solution:

Question 6.
y = \(\log e^{x^{3}} \log x^{3}\)
Solution:

(III) Diffrentiate the following w.r.t. x
Question 1.
y = x2√x + x4 log x
Solution:
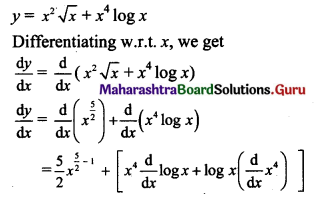

![]()
Question 2.
y = ex sec x – \(x^{\frac{5}{3}}\) log x
Solution:

Question 3.
y = x4 + x√x cos x – x2 ex
Solution:

Question 4.
y = (x3 – 2) tan x – x cos x + 7x . x7
Solution:
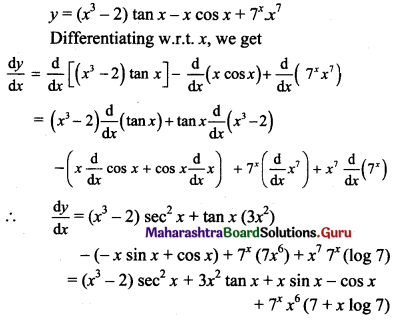
Question 5.
y = sin x log x + ex cos x – ex √x
Solution:
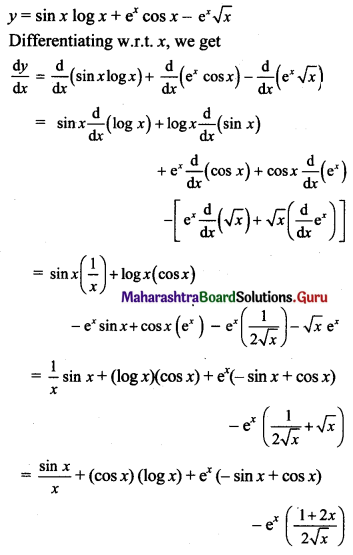
![]()
Question 6.
y = ex tan x + cos x log x – √x 5x
Solution:


(IV) Diffrentiate the following w.r.t.x.
Question 1.
y = \(\frac{x^{2}+3}{x^{2}-5}\)
Solution:

Question 2.
y = \(\frac{\sqrt{x}+5}{\sqrt{x}-5}\)
Solution:
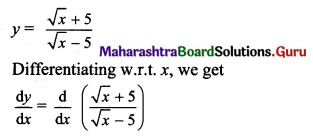

Question 3.
y = \(\frac{x e^{x}}{x+e^{x}}\)
Solution:

![]()
Question 4.
y = \(\frac{x \log x}{x+\log x}\)
Solution:
y = \(\frac{x \log x}{x+\log x}\)
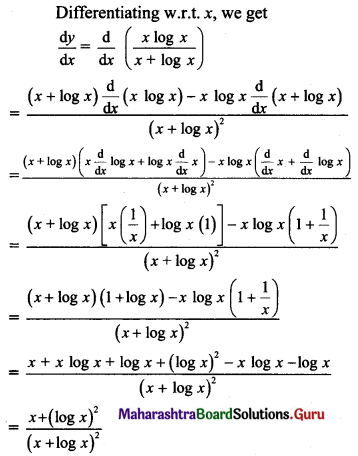
Question 5.
y = \(\frac{x^{2} \sin x}{x+\cos x}\)
Solution:

Question 6.
y = \(\frac{5 e^{x}-4}{3 e^{x}-2}\)
Solution:

(V).
Question 1.
If f(x) is a quadratic polynomial such that f(0) = 3, f'(2) = 2 and f'(3) = 12, then find f(x).
Solution:
Let f(x) = ax2 + bx + c …..(i)
∴ f(0) = a(0)2 + b(0) + c
∴ f(0) = c
But, f(0) = 3 …..(given)
∴ c = 3 …..(ii)
Differentiating (i) w.r.t. x, we get
f'(x) = 2ax + b
∴ f'(2) = 2a(2) + b
∴ f'(2) = 4a + b
But, f'(2) = 2 …..(given)
∴ 4a + b = 2 …..(iii)
Also, f'(3) = 2a(3) + b
∴ f'(3) = 6a + b
But, f'(3) = 12 …..(given)
∴ 6a + b = 12 …..(iv)
equation (iv) – equation (iii), we get
2a = 10
∴ a = 5
Substituting a = 5 in (iii), we get
4(5) + b = 2
∴ b = -18
∴ a = 5, b = -18, c = 3
∴ f(x) = 5x2 – 18x + 3
Check:
If f(0) = 3, f'(2) = 2 and f'(3) = 12, then our answer is correct.
f(x) = 5x2 – 18x + 3 and f'(x) = 10x – 18
f(0) = 5(0)2 – 18(0) + 3 = 3
f'(2) = 10(2) – 18 = 2
f'(3) = 10(3) – 18 = 12
Thus, our answer is correct.
![]()
Question 2.
If f(x) = a sin x – b cos x, f'(\(\frac{\pi}{4}\)) = √2 and f'(\(\frac{\pi}{6}\)) = 2, then find f(x).
Solution:
f(x) = a sin x – b cos x
Differentiating w.r.t. x, we get
f'(x) = a cos x – b (- sin x)
∴ f'(x) = a cos x + b sin x


Now, f(x) = a sin x – b cos x
∴ f(x) = (√3 + 1) sin x + (√3 – 1) cos x
VI. Fill in the blanks. (Activity Problems)
Question 1.
y = ex . tan x
Diff. w.r.t. x
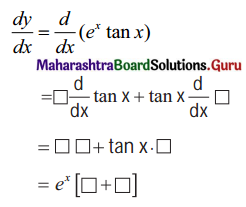
Solution:

Question 2.
y = \(\frac{\sin x}{x^{2}+2}\)
diff. w.r.t. x
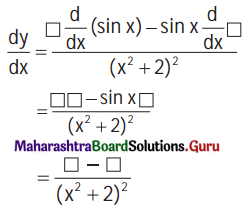
Solution:

![]()
Question 3.
y = (3x2 + 5) cos x
Diff. w.r.t. x
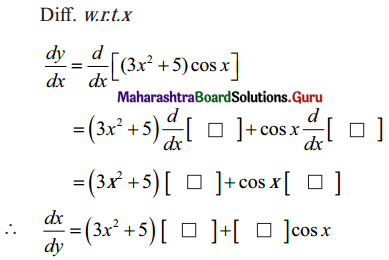
Solution:

Question 4.
Differentiate tan x and sec x w.r.t. x using the formulae for differentiation of \(\frac{u}{v}\) and \(\frac{1}{v}\) respectively.
Solution:

