Maharashtra Board 11th Maths Solutions Chapter 4 Determinants and Matrices Ex 4.1

Balbharti Maharashtra State Board Class 11 Maths Solutions Pdf Chapter 4 Determinants and Matrices Ex 4.1 Questions and Answers.

Maharashtra State Board 11th Maths Solutions Chapter 4 Determinants and Matrices Ex 4.1

Question 1.
Find the values of the determinants.
i. \(\left|\begin{array}{cc}
2 & -4 \\
7 & -15
\end{array}\right|\)
ii. \(\left|\begin{array}{cc}
2 {i} & 3 \\
4 & -{i}
\end{array}\right|\)
iii. \(\left|\begin{array}{ccc}
3 & -4 & 5 \\
1 & 1 & -2 \\
2 & 3 & 1
\end{array}\right|\)
iv. \(\left|\begin{array}{ccc}
\mathbf{a} & \mathbf{h} & \mathbf{g} \\
\mathbf{h} & \mathbf{b} & \mathbf{f} \\
\mathbf{g} & \mathbf{f} & \mathbf{c}
\end{array}\right|\)
Solution:
i. \(\left|\begin{array}{cc}
2 & -4 \\
7 & -15
\end{array}\right|\)
= 2(-15) – (-4)(7)
= -30 + 28
= – 2

ii. \(\left|\begin{array}{cc}
2 {i} & 3 \\
4 & -{i}
\end{array}\right|\)
= 2i(-i) – 3(4)
= -2i² – 12
= -2(-1) – 12 … [∵ i² = -1]
= 2 – 12
= -10

iii. \(\left|\begin{array}{ccc}
3 & -4 & 5 \\
1 & 1 & -2 \\
2 & 3 & 1
\end{array}\right|\)
= \(3\left|\begin{array}{cc}
1 & -2 \\
3 & 1
\end{array}\right|-(-4)\left|\begin{array}{cc}
1 & -2 \\
2 & 1
\end{array}\right|+5\left|\begin{array}{ll}
1 & 1 \\
2 & 3
\end{array}\right|\)
= 3(1 + 6)+ 4(1 + 4)+ 5(3 – 2)
= 3(7) + 4(5) + 5(1)
= 21 + 20 + 5
= 46

iv. \(\left|\begin{array}{ccc}
\mathbf{a} & \mathbf{h} & \mathbf{g} \\
\mathbf{h} & \mathbf{b} & \mathbf{f} \\
\mathbf{g} & \mathbf{f} & \mathbf{c}
\end{array}\right|\) = \({a}\left|\begin{array}{ll}
{b} & {f} \\
{f} & {c}
\end{array}\right|-{h}\left|\begin{array}{ll}
{h} & {f} \\
{g} & {c}
\end{array}\right|+{g}\left|\begin{array}{ll}
{h} & {b} \\
{g} & {f}
\end{array}\right|\)
= a(bc – f²) – h(hc — gf) + g(hf- gb)
= abc – af² – h²c + fgh + fgh – g²b
= abc + 2fgh – af² – bg² – ch²
= (-15) – (-4)(7)
= -30 + 28
= -2

Question 2.
Find the values of x, if
i. \(\left|\begin{array}{cc}
x^{2}-x+1 & x+1 \\
x+1 & x+1
\end{array}\right|=0\)
ii. \(\left|\begin{array}{ccc}
x & -1 & 2 \\
2 x & 1 & -3 \\
3 & -4 & 5
\end{array}\right|=29\)
Solution:
i. \(\left|\begin{array}{cc}
x^{2}-x+1 & x+1 \\
x+1 & x+1
\end{array}\right|=0\)
∴ (x² – x + 1)(x + 1) – (x + 1)(x + 1) = 0
∴ (x + 1)[x² – x + 1 — (x + 1)] = 0
∴ (x + 1)(x² — x + 1 – x- 1) = 0
∴ (x + 1 )(x² – 2x) = 0
∴ (x + 1) x(x – 2) = 0
∴ x = 0 or x + 1 = 0 or x – 2 = 0
∴ x = 0 or x = -1 or x = 2

ii. \(\left|\begin{array}{ccc}
x & -1 & 2 \\
2 x & 1 & -3 \\
3 & -4 & 5
\end{array}\right|=29\) = 29
∴ \(x\left|\begin{array}{cc}
1 & -3 \\
-4 & 5
\end{array}\right|-(-1)\left|\begin{array}{cc}
2 x & -3 \\
3 & 5
\end{array}\right|+2\left|\begin{array}{cc}
2 x & 1 \\
3 & -4
\end{array}\right|=29\)
x(5 – 12) + 1(10x + 9) + 2(-8x – 3) = 29
∴ -7x + 10x + 9 – 16x – 6 = 29
∴ -13x + 3 = 29
∴ -13x = 26
∴ x = -2

Question 3.
Find x and y if \(\left|\begin{array}{ccc}
4 \mathbf{i} & \mathbf{i}^{3} & 2 \mathrm{i} \\
1 & 3 i^{2} & 4 \\
5 & -3 & i
\end{array}\right|\) = x + iy, where i² = -1
Solution:

= 4i(-3i + 12) + i(i – 20) + 2i(-3 + 15)
= 12i² + 48i + i² – 20i + 24i
= -11i² + 52i
= -11(-1) + 52i … [∵ i² = -1]
= 11 + 52i
Comparing with x + iy, we get x = 11, y = 52

Question 4.
Find the minors and cofactors of elements of the determinant D = \(\left|\begin{array}{ccc}
2 & -1 & 3 \\
1 & 2 & -1 \\
5 & 7 & 2
\end{array}\right|\)
Soution:
Here, \(\left|\begin{array}{lll}
a_{11} & a_{12} & a_{13} \\
a_{21} & a_{22} & a_{23} \\
a_{31} & a_{32} & a_{33}
\end{array}\right|=\left|\begin{array}{ccc}
2 & -1 & 3 \\
1 & 2 & -1 \\
5 & 7 & 2
\end{array}\right|\)
M₁₁ = \(\left|\begin{array}{cc}
2 & -1 \\
7 & 2
\end{array}\right|\) = 4 + 7 = 11
C₁₁ = (-1)¹⁺¹M₁₁ = (1)(11) = 11

M₁₂ = \(\left|\begin{array}{cc}
1 & -1 \\
5 & 2
\end{array}\right|\) = 2 + 5 = 7
C₁₂ = = (-1)¹⁺²M₁₂ = (-1)(7) = 11

M₁₃ = \(\left|\begin{array}{cc}
1 & 2 \\
5 & 7
\end{array}\right|\) = 7 – 10 = -3
C₁₃ = = (-1)¹⁺³M₁₃ = (1)(-3) = -3

M₂₁ = \(\left|\begin{array}{cc}
-1 & 3 \\
7 & 2
\end{array}\right|\) = -2 – 21 = 23
C₂₁ = (-1)²⁺¹M₂₁ = (-1)(-23) = 23

M₂₂ = \(\left|\begin{array}{cc}
2 & 3 \\
5 & 2
\end{array}\right|\) = 4 – 15 = -11
C₂₂ = (-1)²⁺²M₂₂ = (1)(-11) = -11

M₂₃ = \(\left|\begin{array}{cc}
2 & -1 \\
5 & 7
\end{array}\right|\) = 14 + 5 = 19
C₂₃ = (-1)¹⁺¹M₂₃ = (1)(11) = 11

M₃₁ = \(\left|\begin{array}{cc}
-1 & 3 \\
1 & -1
\end{array}\right|\) = 1 – 6 = -5
C₃₁ = (-1)³⁺¹M₃₁ = (1)(-5) = -5

M₃₂ = \(\left|\begin{array}{cc}
2 & 3 \\
1 & -1
\end{array}\right|\) = -2 – 3 = -5
C₃₂ = (-1)³⁺²M₃₂ = (-1)(-5) = 5

M₃₃ = \(\left|\begin{array}{cc}
2 & -1 \\
1 & 2
\end{array}\right|\) = 4 + 1 = 5
C₃₃ = (-1)³⁺³M₃₃ = (1)(5) = 5

Question 5.
Evaluate \(\left|\begin{array}{ccc}
2 & -3 & 5 \\
6 & 0 & 4 \\
1 & 5 & -7
\end{array}\right|\) and cofactors of elements in the 2nd determinant and verify:
i. – a₂₁.M₂₁ + a₂₂.M₂₂ – a₂₃.M₂₃ = value of A a₂₁.C₂₁ + a₂₂.C₂₂ + a₂₃.C₂₃ — value of A where M₂₁, M₂₂, M₂₃ are minors of a₂₁, a₂₂, a₂₃ and C₂₁, C₂₂, C₂₃ are cofactors of a₂₁, a₂₂, a₂₃.
Solution:

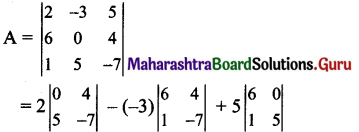
= 2(0 – 20) + 3(- 42 – 4) + 5(30 – 0) = 2(-20) + 3(- 46) + 5(30)
= 2(0 – 20) + 3(- 42 – 4) + 5(30 – 0) = 2(-20) + 3(- 46) + 5(30)
= -40-138+ 150 = -28

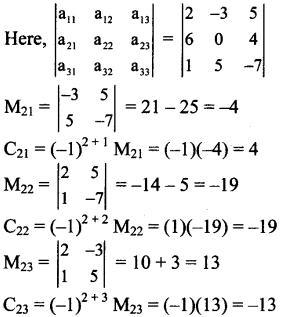
– a₂₁.M₂₁ + a₂₂.M₂₂ – a₂₃.M₂₃
= – (6)(- 4) + (0)(-19) – (4)(13)
= 24 + 0 – 52
= -28
– a₂₁.M₂₁ + a₂₂.M₂₂ – a₂₃.M₂₃ = value of A

ii. a₂₁.C₂₁ + a₂₂.C₂₂ + a₂₃.C₂₃
= (6)(4) +(0)(-19)+ (4)(-13)
= 24 + 0-52 .
= -28
a₂₁.C₂₁ + a₂₂.C₂₂ + a₂₃.C₂₃ = value of A

Question 6.
Find the value of determinant expanding along third column \(\left|\begin{array}{ccc}
-1 & 1 & 2 \\
-2 & 3 & -4 \\
-3 & 4 & 0
\end{array}\right|\)
Solution:
Here, \(\left|\begin{array}{lll}
a_{11} & a_{12} & a_{13} \\
a_{21} & a_{22} & a_{23} \\
a_{31} & a_{32} & a_{33}
\end{array}\right|=\left|\begin{array}{ccc}
-1 & 1 & 2 \\
-2 & 3 & -4 \\
-3 & 4 & 0
\end{array}\right|\)
Expantion along the third column
= a₁₃C₁₃ + a₂₃C₂₃ + a₃₃C₃₃
= 2 x (-1)¹⁺³ \(\left|\begin{array}{ll}
-2 & 3 \\
-3 & 4
\end{array}\right|\)-4 x (-1)²⁺³ \(\left|\begin{array}{ll}
-1 & 1 \\
-3 & 4
\end{array}\right|\) + 0 x (-1)³⁺³ \(\left|\begin{array}{ll}
-1 & 1 \\
-2 & 3
\end{array}\right|\)
= 2 (-8 + 9) +4 (-4 + 3) + O
= 2 – 4
= -2