Balbharati Maharashtra State Board 11th Commerce Maths Solution Book Pdf Chapter 9 Commercial Mathematics Ex 9.4 Questions and Answers.
Maharashtra State Board 11th Commerce Maths Solutions Chapter 9 Commercial Mathematics Ex 9.4
Question 1.
Kanchan purchased a Maruti car for ₹ 2,45,000/- and the rate of depreciation is 14\(\frac{2}{7}\)% per annum. Find the value of the car after two years?
Solution:
Given, purchase price of the car = V = ₹ 2,45,000
Rate of depreciation per annum = r
= 14\(\frac{2}{7}\)%
= \(\frac{100}{7}\)%
∴ Value of the car after two years = \(\mathrm{V}\left(1-\frac{\mathrm{r}}{100}\right)^{\mathrm{n}}\)

∴ The value of the car after two years is ₹ 1,80,000.
Question 2.
The value of a machine depreciates from ₹ 32,768 to ₹ 21,952/- in three years. What is the rate of depreciation?
Solution:
Given, initial value of machine = V = ₹ 32,768/-
Depreciated value of the machine = D.V. = ₹ 21,952/-
Numher of years = n = 3
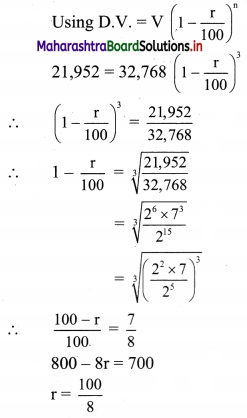
∴ r = 12.5%
∴ Rate of depreciation is 12.5% per annum.
![]()
Question 3.
The value of a machine depreciates at the rate of 10% every year. It was purchased 3 years ago. Its present value is ₹ 2,18,700/-. What was the purchase price of the machine?
Solution:
Given, the rate of depreciation per annum = r = 10%
Number of years = n = 3
Present value of the machine = P.V. = ₹ 2,18,700/-
∴ Purchase price of the machine

∴ The purchase price of the machine is ₹ 3,00,000.
Question 4.
Mr. Manish purchased a motorcycle at ₹ 70,000/-. After some years he sold his motorcycle at its exact depreciated value of it that is ₹ 51,030/-. The rate of depreciation was taken as 10%. Find out how many years he sold his motorcycle.
Solution:
Given, purchase price of the motorcycle = V = ₹ 70,000/-
Depreciated value of the motorcycle = D.V. = ₹ 51,030/-
∴ Rate of depreciation = r = 10%

∴ n = 3
∴ Manish sold his motorcycle after 3 years.
Question 5.
Mr. Chetan purchased furniture for his home at ₹ 5,12,000/-. Considering the rate of depreciation as 12.5%, what will be the value of furniture after 3 years.
Solution:
Given, purchase price of furniture = V = ₹ 5,12,000/-
Rate of depreciation = r = 12.5%
Number of years = n = 3 years
∴ Value of furniture after 3 years = \(\mathrm{V}\left(1-\frac{\mathrm{r}}{100}\right)^{\mathrm{n}}\)
= 5,12,000 \(\left(1-\frac{12.5}{100}\right)^{3}\)
= 5,12,000 \(\left(1-\frac{1}{8}\right)^{3}\)
= 5,12,000 \(\left(\frac{7}{8}\right)^{3}\)
= 5,12,000 × \(\frac{343}{512}\)
= 3,43,000
∴ The value of furniture will be ₹ 3,43,000/-
![]()
Question 6.
Grace Fashion Boutique purchased a sewing machine at ₹ 25,000/-. After 3 years machine was sold at depreciated value of ₹ 18,225/-. Find the rate of depreciation.
Solution:
Given, purchase price of sewing machine = V = ₹ 25,000/-
Selling price of machine = D.V. = ₹ 18,225/-
Number of years = n = 3 years

∴ 100 – r = 90
∴ r = 10%
∴ Rate of depreciation is 10% per annum.
Question 7.
Mr. Pritesh reduced the value of his assets by 5% each year, which were purchased for ₹ 50,00,000/-. Find the value of assets after 2 years.
Solution:
Given, initial value of assets = V = ₹ 50,00,000/-
Rate of depreciation per annum = r = 5%
Number of years = n = 2 years
∴ Value of assets aftertwo years = \(V\left(1-\frac{r}{100}\right)^{n}\)

= 12,500 × 361
= 45,12,500
∴ The value of assets after two years is ₹ 45,12,500/-.
![]()
Question 8.
A manufacturing company is allowed to charge 10% depreciation on its stock. The initial value of the stock was ₹ 60,000/-. After how many years value of the stock will be ₹ 39366?
Solution:
Given, rate of depreciation = r = 10%
Initial value of stock = V = ₹ 60,000
Depreciated value of stock = D.V. = ₹ 39,366/-
By using,

∴ n = 4
∴ The value of the stock will be ₹ 39,366/- after 4 years.