Balbharati Maharashtra State Board 11th Commerce Maths Solution Book Pdf Chapter 6 Permutations and Combinations Ex 6.2 Questions and Answers.
Maharashtra State Board 11th Commerce Maths Solutions Chapter 6 Permutations and Combinations Ex 6.2
Question 1.
Evaluate:
(i) 8!
Solution:
8!
= 8 × 7 × 6 × 5 × 4 × 3 × 2 × 1
= 40320
(ii) 6!
Solution:
6!
= 6 × 5 × 4 × 3 × 2 × 1
= 720
(iii) 8! – 6!
Solution:
8! – 6!
= 8 × 7 × 6! – 6!
= 6! (8 × 7 – 1)
= 6! (56 – 1)
= 6 × 5 × 4 × 3 × 2 × 1 × 55
= 39,600
(iv) (8 – 6)!
Solution:
(8 – 6)!
= 2!
= 2 × 1
= 2
![]()
Question 2.
Compute:
(i) \(\frac{12 !}{6 !}\)
Solution:
\(\frac{12 !}{6 !}\)
= \(\frac{12 \times 11 \times 10 \times 9 \times 8 \times 7 \times 6 !}{6 !}\)
= 12 × 11 × 10 × 9 × 8 × 7
= 665280
(ii) \(\left(\frac{12}{6}\right) !\)
Solution:
\(\left(\frac{12}{6}\right) !\)
= 2!
= 2 × 1
= 2
(iii) (3 × 2)!
Solution:
(3 × 2)!
= 6!
= 6 × 5 × 4 × 3 × 2 × 1
= 720
(iv) 3! × 2!
Solution:
3! × 2!
= 3 × 2 × 1 × 2 × 1
= 12
Question 3.
Compute:
(i) \(\frac{9 !}{3 ! 6 !}\)
Solution:
![]()
(ii) \(\frac{6 !-4 !}{4 !}\)
Solution:
![]()
(iii) \(\frac{8 !}{6 !-4 !}\)
Solution:
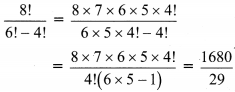
(iv) \(\frac{8 !}{(6-4) !}\)
Solution:
![]()
Question 4.
Write in terms of factorials
(i) 5 × 6 × 7 × 8 × 9 × 10
Solution:
5 × 6 × 7 × 8 × 9 × 10
= 10 × 9 × 8 × 7 × 6 × 5
Multiplying and dividing by 4!, we get
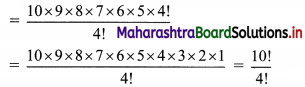
(ii) 3 × 6 × 9 × 12 × 15
Solution:
3 × 6 × 9 × 12 × 15
= 3 × (3 × 2) × (3 × 3) × (3 × 4) × (3 × 5)
= (35) (5 × 4 × 3 × 2 × 1)
= 35 (5!)
![]()
(iii) 6 × 7 × 8 × 9
Solution:
6 × 7 × 8 × 9
= 9 × 8 × 7 × 6
Multiplying and dividing by 5!, we get
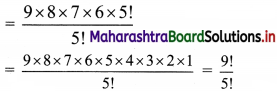
(iv) 5 × 10 × 15 × 20 × 25
Solution:
5 × 10 × 15 × 20 × 25
= (5 × 1) × (5 × 2) × (5 × 3) × (5 × 4) × (5 × 5)
= (55) (5 × 4 × 3 × 2 × 1)
= (55) (5!)
Question 5.
Evaluate: \(\frac{n !}{r !(n-r) !}\) for
(i) n = 8, r = 6
Solution:
n = 8, r = 6

(ii) n = 12, r = 12
Solution:
n = 12, r = 12

Question 6.
Find n, if
(i) \(\frac{n}{8 !}=\frac{3}{6 !}+\frac{1}{4 !}\)
Solution:

(ii) \(\frac{n}{6 !}=\frac{4}{8 !}+\frac{3}{6 !}\)
Solution:
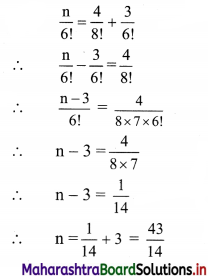
(iii) \(\frac{1}{n !}=\frac{1}{4 !}-\frac{4}{5 !}\)
Solution:

Question 7.
Find n, if
(i) (n + 1)! = 42 × (n – 1)!
Solution:
(n + 1)! = 42(n – 1)!
∴ (n + 1) n (n – 1)! = 42(n – 1)!
∴ n2 + n = 42
∴ n(n + 1) = 6 × 7
Comparing on both sides, we get
∴ n = 6
![]()
(ii) (n + 3)! = 110 × (n + 1)!
Solution:
(n + 3)! = 110 × (n + 1)!
∴ (n + 3) (n + 2) (n + 1)! = 110 (n + 1)!
∴ (n + 3) (n + 2) = (11) (10)
Comparing on both sides, we get
n + 3 = 11
∴ n = 8
Question 8.
Find n, if:
(i) \(\frac{n !}{3 !(n-3) !}: \frac{n !}{5 !(n-5) !}=5: 3\)
Solution:
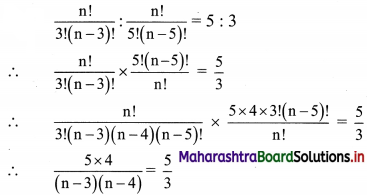
∴ 12 = (n – 3)(n – 4)
∴ (n – 3)(n – 4) = 4 × 3
Comparing on both sides, we get
n – 3 = 4
∴ n = 7
(ii) \(\frac{n !}{3 !(n-5) !}: \frac{n !}{5 !(n-7) !}=10: 3\)
Solution:
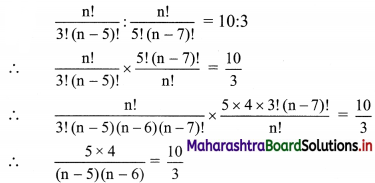
∴ (n – 5) (n – 6) = 3 × 2
Comparing on both sides, we get
n – 5 = 3
∴ n = 8
Question 9.
Find n, if:
(i) \(\frac{(17-n) !}{(14-n) !}\) = 5!
Solution:
\(\frac{(17-n) !}{(14-n) !}\) = 5!
∴ \(\frac{(17-n)(16-n)(15-n)(14-n) !}{(14-n) !}\) = 5 × 4 × 3 × 2 × 1
∴ (17 – n) (16 – n) (15 – n) = 6 × 5 × 4
Comparing on both sides, we get
17 – n = 6
∴ n = 11
(ii) \(\frac{(15-n) !}{(13-n) !}\) = 12
Solution:
\(\frac{(15-n) !}{(13-n) !}\) = 12
∴ \(\frac{(15-\mathrm{n})(14-\mathrm{n})(13-\mathrm{n}) !}{(13-\mathrm{n}) !}\) = 12
∴ (15 – n) (14 – n) = 4 × 3
Comparing on both sides, we get
15 – n = 4
∴ n = 11
Question 10.
Find n if \(\frac{(2 n) !}{7 !(2 n-7) !}: \frac{n !}{4 !(n-4) !}\) = 24 : 1
Solution:

∴ (2n – 1) (2n – 3) (2n – 5) = 9 × 7 × 5
Comparing on both sides, we get
2n – 1 = 9
∴ n = 5
![]()
Question 11.
Show that \(\frac{n !}{r !(n-r) !}+\frac{n !}{(r-1) !(n-r+1) !}=\frac{(n+1) !}{r !(n-r+1)}\)
Solution:

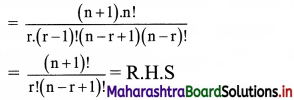
Question 12.
Show that \(\frac{9 !}{3 ! 6 !}+\frac{9 !}{4 ! 5 !}=\frac{10 !}{4 ! 6 !}\)
Solution:

Question 13.
Find the value of:
(i) \(\frac{8 !+5(4 !)}{4 !-12}\)
Solution:

(ii) \(\frac{5(26 !)+(27 !)}{4(27 !)-8(26 !)}\)
Solution:

![]()
Question 14.
Show that
\(\frac{(2 n) !}{n !}\) = 2n (2n – 1) (2n – 3)…5.3.1
Solution:

