Balbharati Maharashtra State Board 11th Commerce Maths Solution Book Pdf Chapter 6 Determinants Ex 6.2 Questions and Answers.
Maharashtra State Board 11th Commerce Maths Solutions Chapter 6 Determinants Ex 6.2
Question 1.
Without expanding, evaluate the following determinants.
(i) \(\left|\begin{array}{lll}
1 & a & b+c \\
1 & b & c+a \\
1 & c & a+b
\end{array}\right|\)
Solution:

(ii) \(\left|\begin{array}{ccc}
2 & 3 & 4 \\
5 & 6 & 8 \\
6 x & 9 x & 12 x
\end{array}\right|\)
Solution:

(iii) \(\left|\begin{array}{lll}
2 & 7 & 65 \\
3 & 8 & 75 \\
5 & 9 & 86
\end{array}\right|\)
Solution:

Question 2.
Using properties of determinants, show that \(\left|\begin{array}{ccc}
a+b & a & b \\
a & a+c & c \\
b & c & b+c
\end{array}\right|\) = 4abc
Solution:

![]()
Question 3.
Solve the following equation.
\(\left|\begin{array}{ccc}
x+2 & x+6 & x-1 \\
x+6 & x-1 & x+2 \\
x-1 & x+2 & x+6
\end{array}\right|=0\)
Solution:
\(\left|\begin{array}{ccc}
x+2 & x+6 & x-1 \\
x+6 & x-1 & x+2 \\
x-1 & x+2 & x+6
\end{array}\right|=0\)
Applying R2 → R2 – R1 and R3 → R3 – R1, we get
\(\left|\begin{array}{ccc}
x+2 & x+6 & x-1 \\
4 & -7 & 3 \\
-3 & -4 & 7
\end{array}\right|=0\)
∴ (x + 2)(-49 + 12) – (x + 6)(28 + 9) + (x – 1)(-16 – 21) = 0
∴ (x + 2) (-37) – (x + 6) (37) + (x – 1) (-37) = 0
∴ -37(x + 2 + x + 6 + x – 1) = 0
∴ 3x + 7 = 0
∴ x = \(\frac{-7}{3}\)
Question 4.
If \(\left|\begin{array}{lll}
4+x & 4-x & 4-x \\
4-x & 4+x & 4-x \\
4-x & 4-x & 4+x
\end{array}\right|=0\), then find the values of x.
Solution:

∴ (12 – x)[1(4x2 – 0) – (4 – x)(0 – 0) + (4 – x)(0 – 0)] = 0
∴ (12 – x)(4x2) = 0
∴ x2(12 – x) = 0
∴ x = 0 or 12 – x = 0
∴ x = 0 or x = 12
Question 5.
Without expanding determinants, show that
\(\left|\begin{array}{ccc}
1 & 3 & 6 \\
6 & 1 & 4 \\
3 & 7 & 12
\end{array}\right|+4\left|\begin{array}{lll}
2 & 3 & 3 \\
2 & 1 & 2 \\
1 & 7 & 6
\end{array}\right|=10\left|\begin{array}{lll}
1 & 2 & 1 \\
3 & 1 & 7 \\
3 & 2 & 6
\end{array}\right|\)
Solution:


Question 6.
Without expanding determinants, find the value of
(i) \(\left|\begin{array}{lll}
10 & 57 & 107 \\
12 & 64 & 124 \\
15 & 78 & 153
\end{array}\right|\)
Solution:

(ii) \(\left|\begin{array}{lll}
2014 & 2017 & 1 \\
2020 & 2023 & 1 \\
2023 & 2026 & 1
\end{array}\right|\)
Solution:

![]()
Question 7.
Without expanding determinants, prove that
(i) \(\left|\begin{array}{lll}
a_{1} & b_{1} & c_{1} \\
a_{2} & b_{2} & c_{2} \\
a_{3} & b_{3} & c_{3}
\end{array}\right|=\left|\begin{array}{lll}
b_{1} & c_{1} & a_{1} \\
b_{2} & c_{2} & a_{2} \\
b_{3} & c_{3} & a_{3}
\end{array}\right|=\left|\begin{array}{lll}
c_{1} & a_{1} & b_{1} \\
c_{2} & a_{2} & b_{2} \\
c_{3} & a_{3} & b_{3}
\end{array}\right|\)
Solution:


(ii) \(\left|\begin{array}{lll}
1 & y z & y+z \\
1 & z x & z+x \\
1 & x y & x+y
\end{array}\right|=\left|\begin{array}{lll}
1 & x & x^{2} \\
1 & y & y^{2} \\
1 & z & z^{2}
\end{array}\right|\)
Solution:
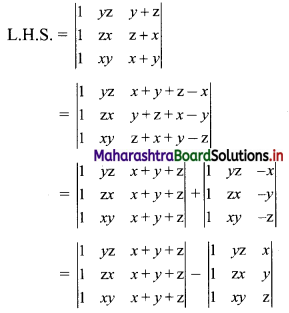
In 1st determinant, taking (x + y + z) common from C3 and in 2nd determinant, taking \(\frac{1}{x}, \frac{1}{y}, \frac{1}{z}\) common from R1, R2, R3 respectively, we get
