Balbharati Maharashtra State Board 11th Commerce Maths Solution Book Pdf Chapter 5 Locus and Straight Line Ex 5.1 Questions and Answers.
Maharashtra State Board 11th Commerce Maths Solutions Chapter 5 Locus and Straight Line Ex 5.1
Question 1.
If A(1, 3) and B(2, 1) are points, find the equation of the locus of point P such that PA = PB.
Solution:
Let P(x, y) be any point on the required locus.
Given, A(1, 3) and B(2, 1).
PA = PB
∴ PA2 = PB2
∴ (x – 1)2 + (y – 3)2 = (x – 2)2 + (y – 1)2
∴ x2 – 2x + 1 + y2 – 6y + 9 = x2 – 4x + 4 + y2 – 2y + 1
∴ -2x – 6y + 10 = -4x – 2y + 5
∴ 2x – 4y + 5 = 0
∴ The required equation of locus is 2x – 4y + 5 = 0.
![]()
Question 2.
A(-5, 2) and B(4, 1). Find the equation of the locus of point P, which is equidistant from A and B.
Solution:
Let P(x, y) be any point on the required locus.
P is equidistant from A(-5, 2) and B(4, 1).
∴ PA = PB
∴ PA2 = PB2
∴ (x + 5)2 + (y – 2)2 = (x – 4)2 + (y – 1)2
∴ x2 + 10x + 25 + y2 – 4y + 4 = x2 – 8x + 16 + y2 – 2y + 1
∴ 10x – 4y + 29 = -8x – 2y + 17
∴ 18x – 2y + 12 = 0
∴ 9x – y + 6 = 0
∴ The required equation of locus is 9x – y – 6 = 0
Question 3.
If A(2, 0) and B(0, 3) are two points, find the equation of the locus of point P such that AP = 2BP.
Solution:
Let P(x, y) be any point on the required locus.
Given, A(2, 0), B(0, 3) and AP = 2BP
∴ AP2 = 4BP2
∴ (x – 2)2 + (y – 0)2 = 4[(x – 0)2 + (y – 3)2]
∴ x2 – 4x + 4 + y2 = 4(x2 + y2 – 6y + 9)
∴ x2 – 4x + 4 + y2 = 4x2 + 4y2 – 24y + 36
∴ 3x2 + 3y2 + 4x – 24y + 32 = 0
∴ The required equation of locus is 3x2 + 3y2 + 4x – 24y + 32 = 0
Question 4.
If A(4, 1) and B(5, 4), find the equation of the locus of point P if PA2 = 3PB2.
Solution:
Let P(x, y) be any point on the required locus.
Given, A(4, 1), B(5, 4) and PA2 = 3PB2
∴ (x – 4)2 + (y – 1)2 = 3[(x – 5)2 + (y – 4)2]
∴ x2 – 8x + 16 + y2 – 2y + 1 = 3(x2 – 10x + 25 + y2 – 8y + 16)
∴ x2 – 8x + y2 – 2y + 17 = 3x2 – 30x + 75 + 3y2 – 24y + 48
∴ 2x2 + 2y2 – 22x – 22y + 106 = 0
∴ x2 + y2 – 11x – 11y + 53 = 0
∴ The required equation of locus is x2 + y2 – 11x – 11y + 53 = 0.
![]()
Question 5.
A(2, 4) and B(5, 8), find the equation of the locus of point P such that PA2 – PB2 = 13.
Solution:
Let P(x, y) be any point on the required locus.
Given, A(2, 4), B(5, 8) and PA2 – PB2 = 13
∴ [(x – 2)2 + (y – 4)2] – [(x – 5)2 + (y – 8)2] = 13
∴ (x2 – 4x + 4 + y2 – 8y + 16) – (x2 – 10x + 25 + y2 – 16y + 64) = 13
∴ 6x + 8y – 69 = 13
∴ 6x + 8y – 82 = 0
∴ 3x + 4y – 41 = 0
∴ The required equation of locus is 3x + 4y – 41 = 0
Question 6.
A(1, 6) and B(3, 5), find the equation of the locus of point P such that segment AB subtends a right angle at P. (∠APB = 90°)
Solution:
Let P(x. y) be any point on the required locus.
Given, A(1, 6) and B(3, 5), ∠APB = 90°
∴ ΔAPB is a right-angled triangle.
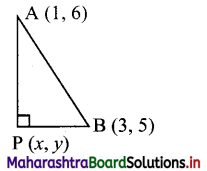
By Pythagoras theorem,
AP2 + PB2 = AB2
∴ [(x – 1)2 + (y – 6)2] + [(x – 3)2 + (y – 5)2] = (1 – 3)2 + (6 – 5)2
∴ x2 – 2x + 1 + y2 – 12y + 36 + x2 – 6x + 9 + y2 – 10y + 25 = 4 + 1
∴ 2x2 + 2y2 – 8x – 22y + 66 = 0
∴ x2 + y2 – 4x – 11y + 33 = 0
∴ The required equation of locus is x2 + y2 – 4x – 11y + 33 = 0
Question 7.
If the origin is shifted to the point O'(2, 3), the axes remaining parallel to the original axes, find the new co-ordinates of the points (a) A(1, 3) (b) B(2, 5)
Solution:
Origin is shifted to (2, 3) = (h, k)
Let the new co-ordinates be (X, Y).
∴ x = X + h and y = Y + k
∴ x = X + 2 and y = Y + 3 …..(i)
(a) Given, A(x, y) = A(1, 3)
x = X + 2 and y = Y + 3 …..[From (i)]
∴ 1 = X + 2 and 3 = Y + 3
∴ X = -1 and Y = 0
∴ the new co-ordinates of point A are (-1, 0).
(b) Given, B(x, y) = B(2, 5)
x = X + 2 andy = Y + 3 ……[From (i)]
∴ 2 = X + 2 and 5 = Y + 3
∴ X = 0 and Y = 2
∴ the new co-ordinates of point B are (0, 2).
![]()
Question 8.
If the origin is shifted to the point O'(1, 3), the axes remaining parallel to the original axes, find the old co-ordinates of the points (a) C(5, 4) (b) D(3, 3)
Solution:
Origin is shifted to (1, 3) = (h, k)
Let the new co-ordinates be (X, Y)
x = X + h and y = Y + k
∴ x = X + 1 and 7 = Y + 3 …..(i)
(a) Given, C(X, Y) = C(5, 4)
∴ x = X + 1 andy = Y + 3 …..[From(i)]
∴ x = 5 + 1 = 6 and y = 4 + 3 = 7
∴ the old co-ordinates of point C are (6, 7).
(b) Given, D(X, Y) = D(3, 3)
∴ x = X + 1 and y = Y + 3 …..[From (i)]
∴ x = 3 + 1 = 4 and y = 3 + 3 = 6
∴ the old co-ordinates of point D are (4, 6).
Question 9.
If the co-ordinates (5, 14) change to (8, 3) by the shift of origin, find the co-ordinates of the point, where the origin is shifted.
Solution:
Let the origin be shifted to (h, k).
Given, (x,y) = (5, 14), (X, Y) = (8, 3)
Since, x = X + h and y = Y + k
∴ 5 = 8 + h and 14 = 3 + k
∴ h = -3 and k = 11
∴ the co-ordinates of the point, where the origin is shifted are (-3, 11).
Question 10.
Obtain the new equations of the following loci if the origin is shifted to the point O'(2, 2), the direction of axes remaining the same:
(a) 3x – y + 2 = 0
(b) x2 + y2 – 3x = 7
(c) xy – 2x – 2y + 4 = 0
Solution:
Given, (h, k) = (2, 2)
Let (X, Y) be the new co-ordinates of the point (x, y).
∴ x = X + h and y = Y + k
∴ x = X + 2 and y = Y + 2
(a) Substituting the values of x and y in the equation 3x – y + 2 = 0, we get
3(X + 2) – (Y + 2) + 2 = 0
∴ 3X + 6 – Y – 2 + 2 = 0
∴ 3X – Y + 6 = 0, which is the new equation of locus.
(b) Substituting the values of x and y in the equation x2 + y2 – 3x = 7, we get
(X + 2)2 + (Y + 2)2 – 3(X + 2) = 7
∴ X2 + 4X + 4 + Y2 + 4Y + 4 – 3X – 6 = 7
∴ X2 + Y2 + X + 4Y – 5 = 0, which is the new equation of locus.
![]()
(c) Substituting the values of x and y in the equation xy – 2x – 2y + 4 = 0, we get
(X + 2) (Y + 2) – 2(X + 2) – 2(Y + 2) + 4 = 0
∴ XY + 2X + 2Y + 4 – 2X – 4 – 2Y – 4 + 4 = 0
∴ XY = 0, which is the new equation of locus.