Balbharati Maharashtra State Board 11th Commerce Maths Solution Book Pdf Chapter 2 Measures of Dispersion Ex 2.2 Questions and Answers.
Maharashtra State Board 11th Commerce Maths Solutions Chapter 2 Measures of Dispersion Ex 2.2
Question 1.
Find the variance and S.D. for the following set of numbers.
7, 11, 2, 4, 9, 6, 3, 7, 11, 2, 5, 8, 3, 6, 8, 8, 2, 6
Solution:
Given data: 7, 11, 2, 4, 9, 6, 3, 7, 11, 2, 5, 8, 3, 6, 8, 8, 2, 6
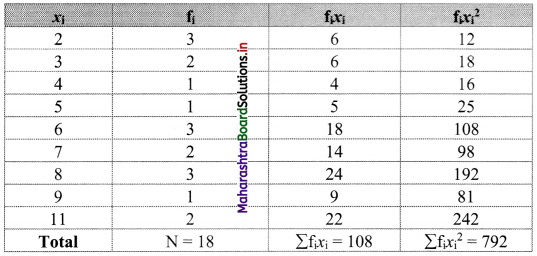
The tabulated form of the above data is as given below:

We prepare the following table for the calculation of variance and S. D.
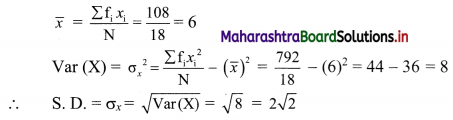
Question 2.
Find the variance and S.D. for the following set of numbers.
65, 77, 81, 98, 100, 80, 129
Solution:
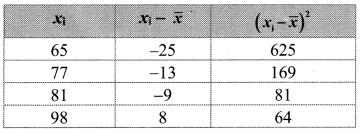

![]()
Question 3.
Compute the variance and standard deviation for the following data:
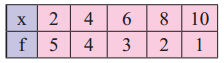
Solution:
We prepare the following table for the calculation of variance and S.D.:
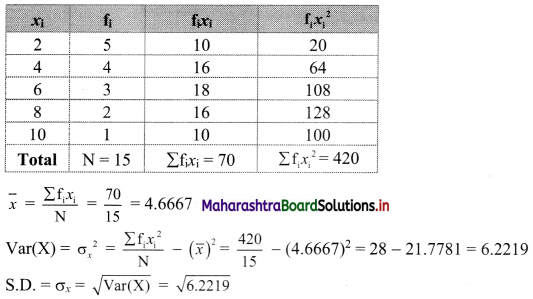
Question 4.
Compute the variance and S.D.

Solution:
We prepare the following table for the calculation of variance and S.D.:

![]()
Question 5.
The following data gives the age of 100 students in a school. Calculate variance and S.D.

Solution:
We prepare the following table for the calculation of variance and S.D:
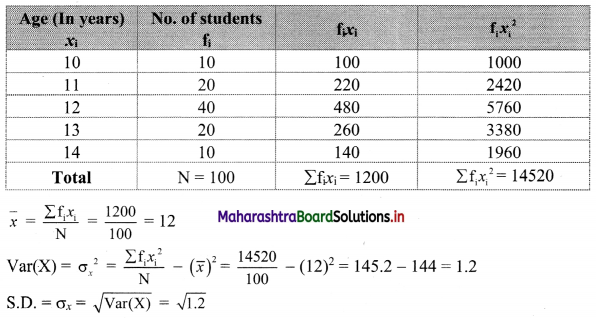
Question 6.
The mean and variance of 5 observations are 3 and 2 respectively. If three of the five observations are 1, 3, and 5, find the values of the other two observations.
Solution:


∴ (x4 – 4)(x4 – 2) = 0
∴ x4 = 4 or x4 = 2
From (i), we get
x5 = 2 or x5 = 4
∴ The two numbers are 2 and 4.
Question 7.
Obtain standard deviation for the following data:
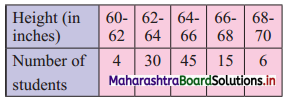
Solution:
We prepare the following table for the calculation of standard deviation.
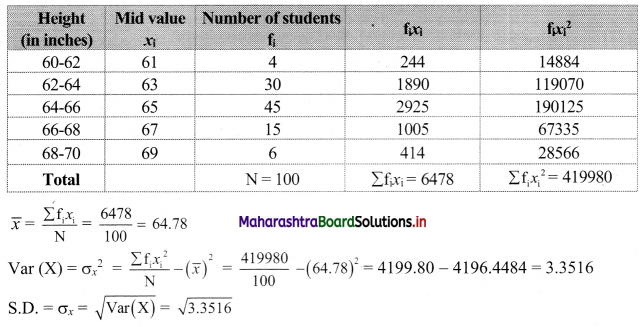
![]()
Question 8.
The following distribution was obtained by change of origin and scale of variable X.

If it is given that mean and variance are 59.5 and 413 respectively, determine actual class intervals.
Solution:
Here, Mean = \(\bar{x}\) = 59.5, and
Var(X) = σ2 = 413
Let xi be a mid value of class and
d = \(\frac{x-a}{h}\), where a is assumed mean and h is class width.
We prepare the following table for calculation of mean and variance of di.
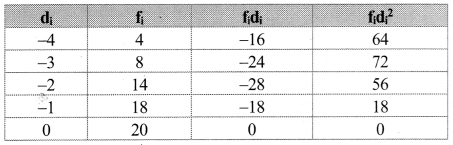

Now, Var(X) = h2. Var(D)
∴ 413 = h2 × 4.13
∴ h2 = 100
∴ h = 10
Substituting h = 10 in (i), we get
-0.1 × 10 + a = 59.5
∴ -1 + a = 59.5
∴ a = 59.5 + 1
∴ a = 60.5
We prepare the following table to determine actual class intervals for corresponding values of di.
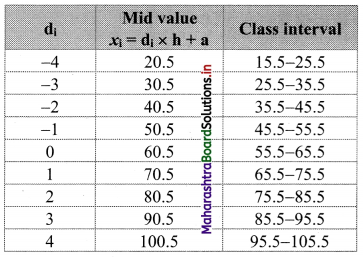
∴ The actual class intervals are 15.5 – 25.5, 25.5 – 35.5, …….., 95.5 – 105.5