Balbharti Maharashtra State Board Class 7 Maths Solutions covers the 7th Std Maths Miscellaneous Problems Set 2 Answers Solutions.
Maharashtra Board Miscellaneous Problems Set 2 Class 7 Maths Solutions
Question 1.
Angela deposited Rs 15000 in a bank at a rate of 9 p.c.p.a. She got simple interest amounting to Rs 5400. For how many years had she deposited the amount?
Solution:
Here, P = Rs 15000, R = 9 p.c.p.a., I = Rs 5400
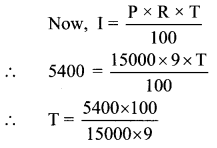
∴ T = 4
∴ Angela had deposited the amount for 4 years.
Question 2.
Ten men take 4 days to complete the task of tarring a road. How many days would 8 men take?
Solution:
Let us suppose that 8 men require x days to tar the road.
Number of days required by 10 men to tar the road = 4
The number of men and the number of days required to tar the road are in inverse proportion.
∴ 8 × x = 10 x 4
∴ \(x=\frac{10 \times 4}{8}\)
∴ x = 5
∴ 8 men will require 5 days to tar the road.
Question 3.
Nasruddin and Mahesh invested Rs 40,000 and Rs 60,000 respectively to start a business. They made a profit of 30%. How much profit did each of them make?
Solution:
Total amount invested = Rs 40,000 + Rs 60,000
= Rs 1,00,000
Profit earned = 30%
∴ Total profit = 30% of 1,00,000
= \(\frac { 30 }{ 100 }\) × 100000
= Rs 30000
Proportion of investment = 40000 : 60000
= 2:3 …. (Dividing by 20000)
Let Nasruddin’s profit be Rs 2x and Mahesh’s profit be Rs 3x.
∴ 2x + 3x = 30000
∴ 5x = 30000
∴ x = \(\frac { 30000 }{ 5 }\).
∴ x = 6000
∴ Nasruddin’s profit = 2x = 2 × 6000 = Rs 12000
Mahesh’s profit = 3x = 3 × 6000 = Rs 18000
∴ The profits of Nasruddin and Mahesh are Rs 12000 and Rs 18000 respectively.
Question 4.
The diameter of a circle is 5.6 cm. Find its circumference.
Solution:
Diameter of the circle (d) = 5.6 cm
Circumference = πd
= \(\frac{22}{7} \times 5.6\)
= \(\frac{22}{7} \times \frac{56}{10}\)
= 17.6 cm
∴ The circumference of the circle is 17.6 cm.
Question 5.
Expand:
i. (2a – 3b)²
ii. (10 + y)²
iii. \(\left(\frac{p}{3}+\frac{q}{4}\right)^{2}\)
iv. \(\left(y-\frac{3}{y}\right)^{2}\)
Solution:
i. Here, A = 2a and B = 3b
∴ (2a – 3b)² = (2a)² – 2 × 2a × 3b + (3b)²
…. [(A – B)² = A² – 2AB + B²]
= 4a² – 12ab + 9b²
ii. Here, a = 10 and b = y
(10 + y)² = 102 + 2 × 10xy + y²
…. [(a + b)² = a² + 2ab + b²]
= 100 + 20y + y²
iii. Here, a = \(\frac { p }{ 3 }\) and b = \(\frac { q }{ 4 }\)
\(\left(\frac{p}{3}+\frac{q}{4}\right)^{2}=\left(\frac{p}{3}\right)^{2}+2 \times \frac{p}{3} \times \frac{q}{4}+\left(\frac{q}{4}\right)^{2}\)
…. [(a + b)² = a² + 2ab + b²]
\(\frac{p^{2}}{9}+\frac{p q}{6}+\frac{q^{2}}{16}\)
iv. Here, a = y and b = \(\frac { 3 }{ y }\)
\(\left(y-\frac{3}{y}\right)^{2}=y^{2}-2 \times y \times \frac{3}{y}+\left(\frac{3}{y}\right)^{2}\)
…. [(a – b)² = a² – 2ab + b²
= \(y^{2}-6+\frac{9}{y^{2}}\)
Question 6.
Use a formula to multiply:
i. (x – 5)(x + 5)
ii. (2a – 13)(2a + 13)
iii. (4z – 5y)(4z + 5y)
iv. (2t – 5)(2t + 5)
Solution:
i. Here, a = x and b = 5
(x – 5)(x + 5) = (x)² – (5)²
…. [(a + b)(a – b) = a² – b²]
= x² – 25
ii. Here, A = 2a and B = 13
(2a – 13)(2a + 13) = (2a)² – (13)²
…. [(A + B)(A – B) = A² – B²]
= 4a² – 169
iii. Here, a = 4z and b = 5y
(4z – 5y)(4z + 5y) = (4z)² – (5y)²
…. [(a + b)(a – b) = a² – b²]
= 16z² – 25y²
iv. Here, a = 2t and b = 5
(2t – 5)(2t + 5) = (2t)² – (5)²
…. [(a + b)(a – b) = a² – b²]
= 4t² – 25
Question 7.
The diameter of the wheel of a cart is 1.05 m. How much distance will the cart cover in 1000 rotations of the wheel?
Solution:
Diameter of the wheel (d) = 1.05 m
∴ Distance covered in 1 rotation of wheel = Circumference of the wheel
= πd
= \(\frac{22}{7} \times 1.05\)
= 3.3 m
∴ Distance covered in 1000 rotations = 1000 x 3.3 m
= 3300 m
= \(\frac { 3300 }{ 1000 }\) km …[1m = \(\frac { 1 }{ 1000 }\)km]
= 3.3 km
∴ The distance covered by the cart in 1000 rotations of the wheel is 3.3 km.
Question 8.
The area of a rectangular garden of length 40 m, is 1000 sq m. Find the breadth of the garden and its perimeter. The garden is to be enclosed by 3 rounds of fencing, leaving an entrance of 4 m. Find the cost of fencing the garden at a rate of Rs 250 per metre.
Solution:
Length of the rectangular garden = 40 m
Area of the rectangular garden = 1000 sq. m.
∴ length × breadth = 1000
∴ 40 × breadth = 1000
∴ breadth = \(\frac { 1000 }{ 40 }\)
= 25 m
Now, perimeter of the rectangular garden = 2 × (length + breadth)
= 2 (40 + 25)
= 2 × 65
= 130 m
Length of one round of fence = circumference of garden – width of the entrance
= 130 – 4
= 126 m
∴ Total length of fencing = length of one round of wire × number of rounds = 126 × 3
= 378 m
∴ Total cost of fencing = Total length of fencing × cost per metre of fencing
= 378 × 250
= 94500
∴ The cost of fencing the garden is Rs 94500.
Question 9.
From the given figure, find the length of hypotenuse AC and the perimeter of ∆ABC.
Solution:
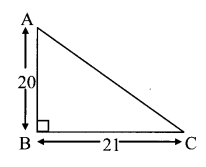
In ∆ABC, ∠B = 90°, and l(BC) = 21, and l(AB) = 20
∴ According to Pythagoras’ theorem,
∴ l(AC)² = l(BC)² + l(AB)²
∴ l(AC)² = 21² + 20²
∴ l(AC)² = 441 + 400
∴ l(AC)² = 841
∴ l(AC)² = 29²
∴ l(AC) = 29
Perimeter of ∆ABC = l(AB) + l(BC) + l(AC)
= 20 + 21 + 29
= 70
∴ The length of hypotenuse AC is 29 units, and the perimeter of ∆ABC is 70 units.
Question 10.
If the edge of a cube is 8 cm long, find its total surface area.
Solution: ,
Total surface area of the cube = 6 × (side)²
= 6 × (8)²
= 6 × 64
= 384 sq. cm
The total surface area of the cube is 384 sq.cm.
Question 11.
Factorize: 365y4z3 – 146y2z4
Solution:
= 365y4z3 – 146y2z4
= 73 (5y4z3 – 2y2z4)
= 73y2 (5y2z3 – 2z4)
= 73y2z3(5y2 – 2z)