Balbharti Maharashtra State Board Class 10 Maths Solutions covers the Practice Set 2.2 Geometry 10th Class Maths Part 2 Answers Solutions Chapter 2 Pythagoras Theorem.
Practice Set 2.2 Geometry 10th Std Maths Part 2 Answers Chapter 2 Pythagoras Theorem
Question 1.
In ∆PQR, point S is the midpoint of side QR. If PQ = 11, PR = 17, PS = 13, find QR.
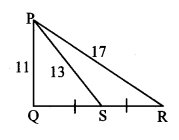
Solution:
In ∆PQR, point S is the midpoint of side QR. [Given]
∴ seg PS is the median.
∴ PQ2 + PR2 = 2 PS2 + 2 SR2 [Apollonius theorem]
∴ 112 + 172 = 2 (13)2 + 2 SR2
∴ 121 + 289 = 2 (169)+ 2 SR2
∴ 410 = 338+ 2 SR2
∴ 2 SR2 = 410 – 338
∴ 2 SR2 = 72
∴ SR2 = \(\frac { 72 }{ 2 } \) = 36
∴ SR = \(\sqrt{36}\) [Taking square root of both sides]
= 6 units Now, QR = 2 SR [S is the midpoint of QR]
= 2 × 6
∴ QR = 12 units
Question 2.
In ∆ABC, AB = 10, AC = 7, BC = 9, then find the length of the median drawn from point C to side AB.
Solution:
Let CD be the median drawn from the vertex C to side AB.
BD = \(\frac { 1 }{ 2 } \) AB [D is the midpoint of AB]
= \(\frac { 1 }{ 2 } \) × 10 = 5 units
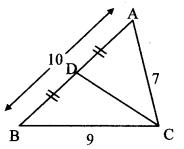
In ∆ABC, seg CD is the median. [Given]
∴ AC2 + BC2 = 2 CD2 + 2 BD2 [Apollonius theorem]
∴ 72 + 92 = 2 CD2 + 2 (5)2
∴ 49 + 81 = 2 CD2 + 2 (25)
∴ 130 = 2 CD2 + 50
∴ 2 CD2 = 130 – 50
∴ 2 CD2 = 80
∴ CD2 = \(\frac { 80 }{ 2 } \) = 40
∴ CD = \(\sqrt { 40 }\) [Taking square root of both sides]
= 2 \(\sqrt { 10 }\) units
∴ The length of the median drawn from point C to side AB is 2 \(\sqrt { 10 }\) units.
Question 3.
In the adjoining figure, seg PS is the median of APQR and PT ⊥ QR. Prove that,
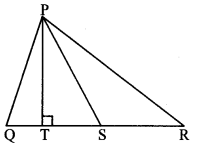
i. PR2 = PS2 + QR × ST + (\(\frac { QR }{ 2 } \))2
ii. PQ2 = PS2 – QR × ST + (\(\frac { QR }{ 2 } \))2
Solution:
i. QS = SR = \(\frac { 1 }{ 2 } \) QR (i) [S is the midpoint of side QR]
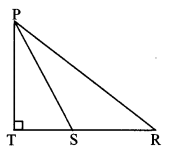
∴ In ∆PSR, ∠PSR is an obtuse angle [Given]
and PT ⊥ SR [Given, Q-S-R]
∴ PR2 = SR2 +PS2 + 2 SR × ST (ii) [Application of Pythagoras theorem]
∴ PR2 = (\(\frac { 1 }{ 2 } \) QR)2 + PS2 + 2 (\(\frac { 1 }{ 2 } \) QR) × ST [From (i) and (ii)]
∴ PR2 = (\(\frac { QR }{ 2 } \))2 + PS2 + QR × ST
∴ PR2 = PS2 + QR × ST + (\(\frac { QR }{ 2 } \))2
ii. In.∆PQS, ∠PSQ is an acute angle and [Given]
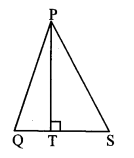
PT ⊥QS [Given, Q-S-R]
∴ PQ2 = QS2 + PS2 – 2 QS × ST (iii) [Application of Pythagoras theorem]
∴ PR2 = (\(\frac { 1 }{ 2 } \) QR)2 + PS2 – 2 (\(\frac { 1 }{ 2 } \) QR) × ST [From (i) and (iii)]
∴ PR2 = (\(\frac { QR }{ 2 } \))2 + PS2 – QR × ST
∴ PR2 = PS2 – QR × ST + (\(\frac { QR }{ 2 } \))2
Question 4.
In ∆ABC, point M is the midpoint of side BC. If AB2 + AC2 = 290 cm, AM = 8 cm, find BC.
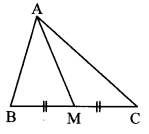
Solution:
In ∆ABC, point M is the midpoint of side BC. [Given]
∴ seg AM is the median.
∴ AB2 + AC2 = 2 AM2 + 2 MC2 [Apollonius theorem]
∴ 290 = 2 (8)2 + 2 MC2
∴ 145 = 64 + MC2 [Dividing both sides by 2]
∴ MC2 = 145 – 64
∴ MC2 = 81
∴ MC = \(\sqrt{81}\) [Taking square root of both sides]
MC = 9 cm
Now, BC = 2 MC [M is the midpoint of BC]
= 2 × 9
∴ BC = 18 cm
Question 5.
In the adjoining figure, point T is in the interior of rectangle PQRS. Prove that, TS2 + TQ2 = TP2 + TR2. (As shown in the figure, draw seg AB || side SR and A – T – B)
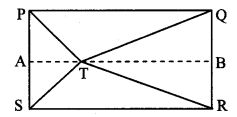
Given: ꠸PQRS is a rectangle.
Point T is in the interior of ꠸PQRS.
To prove: TS2 + TQ2 = TP2 + TR2
Construction: Draw seg AB || side SR such that A – T – B.
Solution:
Proof:
꠸PQRS is a rectangle. [Given]
∴ PS = QR (i) [Opposite sides of a rectangle]
In ꠸ASRB,
∠S = ∠R = 90° (ii) [Angles of rectangle PQRS]
side AB || side SR [Construction]
Also ∠A = ∠S = 90° [Interior angle theorem, from (ii)]
∠B = ∠R = 90°
∴ ∠A = ∠B = ∠S = ∠R = 90° (iii)
∴ ꠸ASRB is a rectangle.
∴ AS = BR (iv) [Opposite sides of a rectanglel
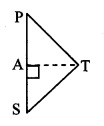
In ∆PTS, ∠PST is an acute angle
and seg AT ⊥ side PS [From (iii)]
∴ TP2 = PS2 + TS2 – 2 PS.AS (v) [Application of Pythagoras theorem]
In ∆TQR., ∠TRQ is an acute angle
and seg BT ⊥ side QR [From (iii)]
∴ TQ2 = RQ2 + TR2 – 2 RQ.BR (vi) [Application of pythagoras theorem]
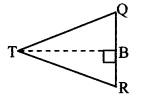
TP2 – TQ2 = PS2 + TS2 – 2PS.AS
-RQ2 – TR2 + 2RQ.BR [Subtracting (vi) from (v)]
∴ TP2 – TQ2 = TS2 – TR2 + PS2
– RQ2 -2 PS.AS +2 RQ.BR
∴ TP2 – TQ2 = TS2 – TR2 + PS2
– PS2 – 2 PS.BR + 2PS.BR [From (i) and (iv)]
∴ TP2 – TQ2 = TS2 – TR2
∴ TS2 + TQ2 = TP2 + TR2
Question 1.
In ∆ABC, ∠C is an acute angle, seg AD Iseg BC. Prove that: AB2 = BC2 + A2 – 2 BC × DC. (Textbook pg. no. 44)
Given: ∠C is an acute angle, seg AD ⊥ seg BC.
To prove: AB2 = BC2 + AC2 – 2BC × DC
Solution:
Proof:
∴ LetAB = c, AC = b, AD = p,
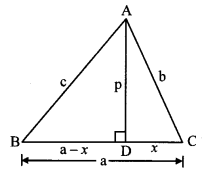
∴ BC = a, DC = x
BD + DC = BC [B – D – C]
∴ BD = BC – DC
∴ BD = a – x
In ∆ABD, ∠D = 90° [Given]
AB2 = BD2 + AD2 [Pythagoras theorem]
∴ c2 = (a – x)2 + [P2] (i)
∴ c2 = a2 – 2ax + x2 + [P2]
In ∆ADC, ∠D = 90° [Given]
AC2 = AD2 + CD2 [Pythagoras theorem]
∴ b2 = p2 + [X2]
∴ p2 = b2 – [X2] (ii)
∴ c2 = a2 – 2ax + x2 + b2 – x2 [Substituting (ii) in (i)]
∴ c2 = a2 + b2 – 2ax
∴ AB2 = BC2 + AC2 – 2 BC × DC
Question 2.
In ∆ABC, ∠ACB is an obtuse angle, seg AD ⊥ seg BC. Prove that: AB2 = BC2 + AC2 + 2 BC × CD. (Textbook pg. no. 40 and 4.1)
Given: ∠ACB is an obtuse angle, seg AD ⊥ seg BC.
To prove: AB2 = BC2 + AC2 + 2BC × CD
Solution:
Proof:
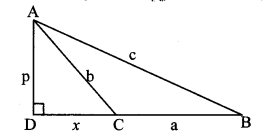
Let AD = p, AC = b, AB = c,
BC = a, DC = x
BD = BC + DC [B – C – D]
∴ BD = a + x
In ∆ADB, ∠D = 90° [Given]
AB2 = BD2 + AD2 [Pythagoras theorem]
∴ c2 = (a + x)2 + p2 (i)
∴ c2 = a2 + 2ax + x2 + p2
Also, in ∆ADC, ∠D = 90° [Given]
AC2 = CD2 + AD2 [Pythagoras theorem]
∴ b2 = x2 + p2
∴ p2 = b2 – x2 (ii)
∴ c2 = a2 + 2ax + x2 + b2 – x2 [Substituting (ii) in (i)]
∴ c2 = a2 + b2 + 2ax
∴ AB2 = BC2 + AC2 + 2 BC × CD
Question 3.
In ∆ABC, if M is the midpoint of side BC and seg AM ⊥seg BC, then prove that
AB2 + AC2 = 2 AM2 + 2 BM2. (Textbook pg, no. 41)
Given: In ∆ABC, M is the midpoint of side BC and seg AM ⊥ seg BC.
To prove: AB2 + AC2 = 2 AM2 + 2 BM2
Solution:
Proof:
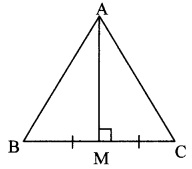
In ∆AMB, ∠M = 90° [segAM ⊥ segBC]
∴ AB2 = AM2 + BM2 (i) [Pythagoras theorem]
Also, in ∆AMC, ∠M = 90° [seg AM ⊥ seg BC]
∴ AC2 = AM2 + MC2 (ii) [Pythagoras theorem]
∴ AB2 + AC2 = AM2 + BM2 + AM2 + MC2 [Adding (i) and (ii)]
∴ AB2 + AC2 = 2 AM2 + BM2 + BM2 [∵ BM = MC (M is the midpoint of BC)]
∴ AB2 + AC2 = 2 AM2 + 2 BM2