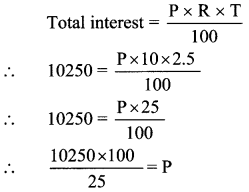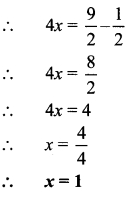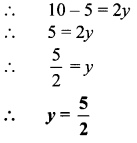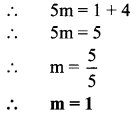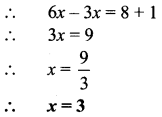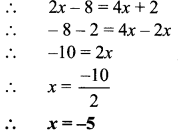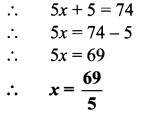Class 7

Balbharti Maharashtra State Board Class 7 Maths Solutions covers the 7th Std Maths Practice Set 44 Answers Solutions Chapter 12 Perimeter and Area.

Perimeter and Area Class 7 Practice Set 44 Answers Solutions Chapter 12

Question 1.
If the length and breadth of a rectangle are doubled, how many times the perimeter of the old rectangle will that of the new rectangle be?
Solution:
Let the length of the old rectangle be l and breadth be b.
∴ Perimeter of old rectangle = 2(l + b)
Length of new rectangle = 2l and breadth = 2b
∴ Perimeter of new rectangle = 2(2l + 2b)
= 2 x 2 (l + b)
= 2 x perimeter of old rectangle
∴ The perimeter of new rectangle will be twice the perimeter of old rectangle.

Question 2.
If the side of a square is tripled, how many times the perimeter of the first square will that of the new square be?
Solution:
Let the length of the square be a.
Perimeter of square = 4 x side
= 4 x a = 4a
Side of new square = 3 x a = 3a
Perimeter of new square = 4 x side
= 4 x 3a = 3 x 4a = 3x perimeter of original square.
∴ The perimeter of new square will be three times the perimeter of original square.

Question 3.
Given alongside is the diagram of a playground. It shows the length of its sides. Find the perimeter of the playground.

Solution:

Side AF = side BC + side DE
∴ Side AF = 15 + 15 = 30 m
Side FE = side AB + side CD
∴ Side FE = 10 + 5 = 15 m
∴ Perimeter of the playground = side AB + side BC + side CD + side DE + side FE + side AF
= 10 + 15 + 5 + 15 + 15 + 30
= 90 m.
∴ The perimeter of the playground is 90 m.

Question 4.
As shown in the figure, four napkins all of the same size were made from a square piece of cloth of length 1 m. What length of lace will be required to trim all four sides of all the napkins?

Solution:
Side of the square piece of cloth = 1 m
∴ Side of each napkin = 0.5 m
Length of lace that will be required for 1 napkin = perimeter of the napkin
= 4 x side = 4 x 0.5 = 2 m
∴ Perimeter of 4 napkins = 4 x 2 = 8 m
∴ 8 metre long lace will be required to trim all four napkins.

Balbharti Maharashtra State Board Class 7 Maths Solutions covers the 7th Std Maths Practice Set 41 Answers Solutions Chapter 10 Bank and Simple Interest.

Bank and Simple Interest Class 7 Practice Set 41 Answers Solutions Chapter 10

Question 1.
If the interest on Rs 1700 is Rs 340 for 2 years, the rate of interest must be__.
(A) 12%
(B) 15%
(C) 4%
(D) 10%
Solution:
(D) 10%

Hint:
∴ \(\text { Total interest }=\frac{P \times R \times T}{100}\)
∴ \(340=\frac{1700 \times R \times 2}{100}\)
∴ R = 10%

Question 2.
If the interest on Rs 3000 is Rs 600 at a certain rate for a certain number of years, what would the interest be on Rs 1500 under the same conditions?
(A) Rs 300
(B) Rs 1000
(C) Rs 700
(D) Rs 500
Solution:
(A) Rs 300

Hint:
The interest on Rs 3000 at certain rate of interest is Rs 600.
Let us suppose the interest on Rs 1500 at the same rate is x.
∴ \(\frac{600}{3000}=\frac{x}{1500}\)
∴ x = Rs 300

Question 3.
Javed deposited Rs 12000 at 9 p.c.p.a in a bank for some years, and withdrew his interest every year. At the end of the period, he had received altogether Rs 17,400. For how many years had he deposited his money?
Solution:
Here, P = Rs 12000, R = 9 p.c.p.a and amount = Rs 17400
Amount = Principal + Interest
∴17400 = 12000 + Interest
∴Interest = 17400 – 12000 = Rs 5400
∴ \(\text { Total interest }=\frac{P \times R \times T}{100}\)
\(5400=\frac{12000 \times 9 \times \mathrm{T}}{100}\)
∴ \(\frac{5400 \times 100}{12000 \times 9}=\mathrm{T}\)
∴ T = 5 years
∴ Javed had deposited the amount for 5 years.

Question 4.
Lataben borrowed some money from a bank at a rate of 10 p.c.p.a interest for \(2\frac { 1 }{ 2 }\) years to start a cottage industry. If she paid Rs 10250 as total interest, how much money had she borrowed?
Solution:
Here, R = 10 p.c.p.a, T = 2.5 years, I = Rs 10250

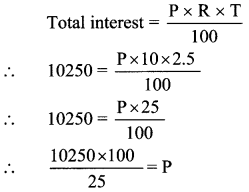
∴ P = Rs 41000
∴ Lataben had borrowed an amount of Rs 41000 from the bank.

Question 5.
Fill in the blanks in the table.

Solution:
i. \(\text { Total interest }=\frac{P \times R \times T}{100}\)
= \(\frac{4200 \times 7 \times 3}{100}\)
= Rs 882
Amount = Principal + interest
= 4200 + 882
= Rs 5082

ii. \(\text { Total interest }=\frac{P \times R \times T}{100}\)
∴ \(1200=\frac{\mathrm{P} \times 6 \times 4}{100}\)
∴ \(\frac{1200 \times 100}{6 \times 4}=\mathrm{P}\)
∴ P = Rs 5000
Amount = Principal + interest
= 5000 + 1200
= Rs 6200

iii. \(\text { Total interest }=\frac{P \times R \times T}{100}\)
∴ \(800=\frac{8000 \times 5 \times \mathrm{T}}{100}\)
∴ \(\frac{800 \times 100}{8000 \times 5}=\mathrm{T}\)
∴ T = 2 years
Amount = Principal + interest
= 8000 + 800
= Rs 8800

iv. Amount = Principal + interest
∴ 18000 = Principal + 6000
∴ Principal = Rs 12000
\(\text { Total interest }=\frac{P \times R \times T}{100}\)
∴ \(6000=\frac{12000 \times 5 \times \mathrm{T}}{100}\)
∴ \(\frac{6000 \times 100}{12000 \times 5}=\mathrm{T}\)
∴ T = 10 years

v. R = \(2\frac { 1 }{ 2 }\) % = 2.5 %
∴ \(\text { Total interest }=\frac{P \times R \times T}{100}\)
∴ \(2400=\frac{\mathrm{P} \times 2.5 \times 5}{100}\)
∴ \(2400=\frac{P \times 25 \times 5}{100 \times 10}\)
∴ \(\frac{2400 \times 10 \times 100}{25 \times 5}=P\)
∴ P = Rs 19200
Amount = Principal + interest
= 19200 + 2400
= Rs 21600

Maharashtra Board Class 7 Maths Chapter 10 Banks and Simple Interest Practice Set 41 Intext Questions and Activities

Question 1.
Ask an adult in your house to show you a passbook and explain the entries made in it. (Textbook pg. no. 70)
Solution:
(Students should attempt the above activities with the help of their parent / teacher.)

Question 2.
Visit different banks and find out the rates of the interest they give for different types of accounts. (Textbook pg. no. 74)
Solution:
(Students should attempt the above activities with the help of their parent / teacher.)

Question 3.
With the help of your teachers, start a Savings Bank in your school and open an account in it to save up some money. (Textbook pg. no. 74)
Solution:
(Students should attempt the above activities with the help of their parent / teacher.)

Balbharti Maharashtra State Board Class 7 Maths Solutions covers the 7th Std Maths Practice Set 38 Answers Solutions Chapter 9 Direct Proportion and Inverse Proportion.

Direct Proportion and Inverse Proportion Class 7 Practice Set 38 Answers Solutions Chapter 9

Question 1.
Five workers take 12 days to weed a field. How many days would 6 workers take? How many would 15 take?
Solution:
Let 6 workers take x days and 15 workers take y days to weed the field.
The number of workers and the time required to weed the field are in inverse proportion.
∴ 6 × x = 5 × 12
∴ \(x=\frac{5 \times 12}{6}\)
∴ x = 10 days
Also, 15 × y = 5 × 12
∴ \(y=\frac{5 \times 12}{15}\)
= 4 days
∴ 6 workers will take 10 days and 15 workers will take 4 days to weed the field.

Question 2.
Mohanrao took 10 days to finish a book, reading 40 pages every day. How many pages must he read in a day to finish it in 8 days?
Solution:
Let Mohanrao read x pages every day to finish the book in 8 days.
The number of pages read per day and the days required to finish the book are in inverse proportion.
∴ 8 × x = 10 × 40
∴ \(x=\frac{10 \times 40}{8}\)
= 50
∴ Mohanrao will have to read 50 pages every day to finish the book in 8 days.

Question 3.
Mary cycles at 6 km per hour. How long will she take to reach her Aunt’s house which is 12 km away? If she cycles at a speed of 4 km/hr, how long would she take?
Solution:
Speed of the cycle = 6 km / hr
Distance travelled to reach her Aunt’s house = 12 km
∴ \(\text { Time required }=\frac{\text { Distance travelled }}{\text { Speed }}\)
= \(\frac { 12 }{ 6 }\)
= 2 hours
Let the time required when the speed of the cycle is 4 km/hr be x hours.
The speed of the cycle and the time required to travel the same distance are in inverse proportion.
∴ 4 × x = 6 × 2
∴ \(x=\frac{6 \times 2}{4}\) = 3 hours
∴ Mary will require 2 hours if she is cycling at 6 km/hr and 3 hours if she is cycling at 4 km/hr to reach her Aunt’s house.

Question 4.
The stock of grain in a government warehouse lasts 30 days for 4000 people. How many days will it last for 6000 people?
Solution:
Let the stock of grain last for x days for 6000 people.
The number of people and the days for which stock will last are in inverse proportion.
∴ 6000 × x = 4000 × 30
∴ \(x=\frac{4000 \times 30}{6000}=20\)
∴ The stock of grain will last for 20 days for 6000 people.

Maharashtra Board Class 7 Maths Chapter 9 Direct Proportion and Inverse Proportion Practice Set 38 Intext Questions and Activities

Question 1.
Students of a certain school went for a picnic to a farm by bus. Here are some of their experiences. Say whether the quantities in each are in direct or in inverse proportion.
(Textbook pg. no. 65 and 66)
i. Each student paid Rs 60 for the expenses.
As there were 45 students,___rupees were collected.
Had there been 50 students,___rupees would have been collected.
The number of students and money collected are in___proportion.

ii. The sweets shop near the school gave 90 laddoos for the picnic.
If 45 students go for the picnic, each will get___laddoos.
If 30 students go for the picnic, each will get___laddoos.
The number of students and that of laddoos each one gets are in___proportion.

iii. The farm is 120 km away from the school.
The bus went to the farm at a speed of 40 km per hour and took___hours.
On the return trip, the speed was 60 km per hour. Therefore, it took___hours.
The speed of the bus and the time it takes are in___proportion.

iv. The farmer picked 180 bors from his trees.
He gave them equally to 45 students. Each student got___bors.
Had there been 60 students, each would have got___bors.
The number of students and the number of bors each one gets are in___proportion.
Solution:
i. Rs 2700, Rs 3000, direct
ii. 2,3, inverse
iii. 3,2, inverse
iv. 4,3, inverse

Balbharti Maharashtra State Board Class 7 Maths Solutions covers the 7th Std Maths Practice Set 39 Answers Solutions Chapter 9 Direct Proportion and Inverse Proportion.

Direct Proportion and Inverse Proportion Class 7 Practice Set 39 Answers Solutions Chapter 9

Question 1.
Suresh and Ramesh together invested Rs 144000 in the ratio 4 : 5 and bought a plot of land. After some years they sold it at a profit of 20%. What is the profit each of them got?
Solution:
Total investment = Rs 144000
Profit earned = 20%
∴ Total profit = 20% of 144000 = \(\frac{20}{100} \times 144000\) = Rs 28800
Proportion of investment of Suresh and Ramesh = 4:5
Let the profit of Suresh be Rs 4x and that of Ramesh be Rs 5x.
4x + 5x = 28800
∴ 9x = 28800
∴ \(x=\frac { 28800 }{ 9 }\)
= 3200
∴ Suresh’s profit = 4x = 4 × 3200 = Rs 12800
Ramesh’s profit = 5x = 5 × 3200 = Rs 16000
∴ The profit earned by Suresh and Ramesh are Rs 12800 and Rs 16000 respectively.

Question 2.
Virat and Samrat together invested Rs 50000 and Rs 120000 to start a business. They suffered a loss of 20%. How much loss did each of them incur?
Solution:
Total investment = Rs 50000 + Rs 120000 = Rs 170000
Loss incurred = 20%
∴ Total loss = 20% of 170000 = \(\frac{20}{100} \times 170000\) = Rs 34000
Proportion of investment = 50000 : 120000
= 5 : 12 …. (Dividingby 10000)
Let the loss incurred by Virat be Rs 5x and that by Samrat be Rs 12x.
5x + 12x = 34000
∴ 17x = 34000
∴ \(x=\frac { 34000 }{ 17 }=2000\)
∴ Virat’s loss = 5x = 5 × 2000 = Rs 10000
Samrat’s loss = 12x = 12 × 2000 = Rs 24000
∴ The loss incurred by Virat and Samrat are Rs 10000 and Rs 24000 respectively.

Question 3.
Shweta, Piyush and Nachiket together invested Rs 80000 and started a business of selling sheets and towels from Solapur. Shweta’s share of the capital was Rs 30000 and Piyush’s Rs 12000. At the end of the year they had made a profit of 24%. What was Nachiket’s investment and what was his share of the profit?
Solution:
Total investment = Rs 80000
Nachiket’s investment = Total investment – (Shweta’s investment + Piyush’s investment)
= 80000 – (30000+ 12000)
= 80000 – 42000 = Rs 38000
Profit earned = 24%
∴ Total profit = 24% of 80000 = \(\frac { 24 }{ 100 }\) x 80000 = Rs 19200
Proportion of investment = 30000 : 12000 : 38000
= 15 : 6 : 19 …. (Dividing by 2000)
Let the profit of Shweta, Piyush and Nachiket be Rs 15x, Rs 6x and Rs 19x respectively.
15x + 6x + 19x = 19200
∴ 40x = 19200
∴ \(x=\frac { 19200 }{ 40 }=480\)
∴ Nachiket’s profit = 19x = 19 × 480 = Rs 9120
∴ Nachiket’s investment is Rs 38000 and his profit is Rs 9120.

Question 4.
A and B shared a profit of Rs 24500 in the proportion 3 : 7. Each of them gave 2% of his share of the profit to the Soldiers’ Welfare Fund. What was the actual amount given to the Fund by each of them?
Solution:
Proportion of share = 3:7
Let the profits of A and B be Rs 3x and Rs 7x respectively.
3x + 7x = 24500
∴ 10x = 24500
∴ \(x=\frac { 24500 }{ 10 }=2450\)
Profit earned by A = 3x = 3 × 2450 = Rs 7350
Amount given by A = 2% of his profit
= \(\frac { 2 }{ 100 }\) × 7350 = Rs 147
Profit earned by B = 7x = 7 × 2450 = Rs 17150
Amount given by B = 2% of his profit
= \(\frac { 2 }{ 100 }\) × 17150 = Rs 343
∴ The amount given by A and B to the Soldiers’ Welfare Fund are Rs 147 and Rs 343 respectively.

Question 5.
Jaya, Seema, Nikhil and Neelesh put in altogether Rs 360000 to form a partnership, with their investments being in the proportion 3 : 4 : 7 : 6. What was Jaya’s actual share in the capital? They made a profit of 12%. How much profit did Nikhil make?
Solution:
Total investment = Rs 360000
Profit earned = 12%
∴ Total profit = 12% of 360000
= \(\frac{12}{100} \times 360000\) = Rs 43200
Proportion of investment = 3 : 4 : 7 : 6
Let the investment of Jaya, Seema, Nikhil and Neelesh be Rs 3x, Rs 4x, Rs 7x and Rs 6x respectively.
3x + 4x + 7x + 6x = 360000
∴ 20x = 360000
∴ \(x=\frac { 360000 }{ 20 }\)
= 18000
∴ Jaya’s investment = 3x = 3 x 18000 = Rs 54000
Also, profit made by them is Rs 43200
∴ 3x + 4x + 7x + 6x = 43200
∴ 20x = 43200
∴ \(x=\frac { 43200 }{ 20 }\)
= 2160
∴ Nikhil’s profit = 7x = 7 x 2160 = Rs 15120
∴ Jaya’s share in the capital was Rs 54000 and the profit made by Nikhil was Rs 15120.

Maharashtra Board Class 7 Maths Chapter 9 Direct Proportion and Inverse Proportion Practice Set 39 Intext Questions and Activities

Question 1.
Saritaben, Ayesha and Meenakshi started a business by investing Rs 2400, Rs 5200 and Rs 3400. They made a profit of 50%. If they reinvested all their profit by adding it to the capital, find out the proportions of their shares in the capital during the following year. (Textbook pg. no. 67)
Solution:
Total investment = Rs 2400 + Rs 5200 + Rs 3400 = Rs 11000
Total profit = 50% of 11000 = \(\frac{50}{100} \times 11000\) = Rs 5500
Proportion of shares = 2400 : 5200 : 3400
= 12 : 26 : 17 …. (Dividingby 200)
Let the profit of Saritaben, Ayesha and Meenakshi be Rs 12x, Rs 26x and Rs 17x respectively.
12x + 26x + 17x = 5500
∴ 55x = 5500
∴ x = 100
∴ Saritaben’s profit = 12x = 12 × 100 = Rs 1200
Ayesha’s profit = 26x = 26 × 100 = Rs 2600
Meenakshi’s profit = 17x = 17 × 100 = Rs 1700
∴ Saritaben’s new investment = 2400 + 1200 = Rs 3600
Ayesha’s new investment = 5200 + 2600 = Rs 7800
Meenakshi’s new investment = 3400 + 1700 = Rs 5100
∴ New proportion of shares = 3600 : 7800 : 5100
= 12 : 26 : 17 …. (Dividing by 300)
∴ The proportion of the shares in the capital during the following year is 12 : 26 :17

Question 2.
Are the amount of petrol filled in a motorcycle and the distance traveled by it, in direct proportion? (Textbook pg. no. 63)
Solution:
Yes.
If amount of petrol filled in the motorcycle is less, it will travel less distance and if the amount of petrol filled is more, it will travel more distance.
Hence, the amount of petrol filled in the motorcycle and the distance traveled by it are in direct proportion.

Question 3.
Can you give examples from science or everyday life of quantities that vary in direct proportion? (Textbook pg. no. 63)
Solution:

1. Number of chairs and the number of spectators.
2. Quantity (litres) of water and number of vessels required to store the water.

Balbharti Maharashtra State Board Class 7 Maths Solutions covers the 7th Std Maths Practice Set 37 Answers Solutions Chapter 37 Direct Proportion and Inverse Proportion.

Direct Proportion and Inverse Proportion Class 7 Practice Set 37 Answers Solutions Chapter 9

Question 1.
If 7 kg onions cost Rs 140, how much must we pay for 12 kg onions?
Solution:
Let the cost of 12 kg onions be Rs x.
The quantity of onions and their cost are in direct proportion.
∴ \(\frac{7}{140}=\frac{12}{x}\)
∴ 7x = 12 × 140 ….(Multiplying both sides by 140x)
∴ x = \(\frac { 12\times 140 }{ 7 }\)
= 240
We must pay Rs 240 for 12 kg onions.

Question 2.
If Rs 600 buy 15 bunches of feed, how many will Rs 1280 buy?
Solution:
Let the bunches of feed bought for Rs 1280 be x.
The quantity of feed bought and their cost are in direct proportion.
∴ \(\frac{600}{15}=\frac{1280}{x}\)
∴ 600x = 1280 × 15 …. (Multiplying both sides by 15x)
∴ \(x=\frac{1280 \times 15}{600}=32\)
∴ 32 bunches of feed can be bought for Rs 1280.

Question 3.
For 9 cows, 13 kg 500 g of food supplement are required every day. In the same proportion, how much will be needed for 12 cows?
Solution:
Let the food supplement required for 12 cows be x kg.
The quantity of food supplement required and the number of cows are in direct proportion.
∴ \(\frac{13 \mathrm{kg} 500 \mathrm{gram}}{9}=\frac{x \mathrm{kg}}{12}\)
∴ \(\frac{13.5}{9}=\frac{x}{12}\) ….(13 kg 500 gram = 13.5 kg)
∴ 13.5 × 12 = 9x ….(Multiplying both sides by 9 x 12)
∴ \(\frac{13.5 \times 12}{9}=x\)
∴ x = 18
∴ The food supplement required for 12 cows is 18 kg.

Question 4.
The cost of 12 quintals of soyabean is Rs 36,000. How much will 8 quintals cost?
Solution:
Let the cost of 8 quintals of soyabean be Rs x.
The quantity of soyabeans and their cost are in direct proportion.
∴ \(\frac{12}{36000}=\frac{8}{x}\)
∴ 12x = 8 × 36000 ….(Multiplying both sides by 36000x)
∴ \(x=\frac{8 \times 36000}{12}=24000\)
∴ The cost of 8 quintals of soyabean is Rs 24000.

Question 5.
Two mobiles cost Rs 16,000. How much money will be required to buy 13 such mobiles ?
Solution:
Let the cost of 13 mobiles be Rs x.
The quantity of mobiles and their cost are in direct proportion.
∴ \(\frac{2}{16000}=\frac{13}{x}\)
∴ 2x = 13 × 16000 ….(Multiplying both sides by 16000x)
∴ \(x=\frac{13 \times 16000}{2}=104000\)
∴ Rs 104000 will be required to buy 13 mobiles.

Balbharti Maharashtra State Board Class 7 Maths Solutions covers the 7th Std Maths Practice Set 35 Answers Solutions Chapter 8 Algebraic Expressions and Operations on them.

Algebraic Expressions and Operations on them Class 7 Practice Set 35 Answers Solutions Chapter 8

Question 1.
Multiply:
i. 16xy × 18xy
ii. 23xy² × 4yz²
iii. (12a + 17b) × 4c
iv. (4x + 5y) × (9x + 7y)
Solution:
i. 16xy × 18xy
= 16 × 18 × xy × xy
= 288x²y²

ii. 23xy² × 4yz²
= 23 × 4 × xy² × yz²
= 92xy³z²

iii. (12a + 17b) × 4c = 12a × 4c + 17b × 4c
= 48ac + 68bc

iv. (4x + 5y) × (9x + 7y)
= 4x × (9x + 7y) + 5y × (9x + 7y)
= (4x × 9x) + (4x × 7y) + (5y × 9x) + (5y × 7y)
= 36x² + 28xy + 45xy + 35y²
= 36x² + 73xy + 35y²

Question 2.
A rectangle is (8x + 5) cm long and (5x + 3) cm broad. Find its area. Solution:
Length of the rectangle = (8x + 5) cm
Breadth of the rectangle = (5x + 3) cm
∴ Area of the rectangle = length × breadth
= (8x + 5) × (5x + 3)
= 8x × (5x + 3) + 5 × (5x + 3)
= (8x × 5x) + (8x × 3) + (5 × 5x) + (5 × 3)
= 40x² + 24x + 25x + 15
= 40x² + 49x + 15
∴ The area of the rectangle is (40x² + 49x + 15) sq. cm.

Balbharti Maharashtra State Board Class 7 Maths Solutions covers the 7th Std Maths Practice Set 36 Answers Solutions Chapter 8 Algebraic Expressions and Operations on them.

Algebraic Expressions and Operations on them Class 7 Practice Set 36 Answers Solutions Chapter 8

Question 1.
Simplify (3x – 11y) – (17x + 13y) and choose the right answer.
(A) 7x – 12y
(B) -14x – 54y
(C) -3(5x + 4y)
(D) -2(7x + 12y)
Solution:
(D) -2(7x + 12y)

Hints:
(3x – 11y) – (17x + 13y) = 3x – 11y – 17x – 13y
= – 14x – 24y
= – 2 × 7x – 2 × 12y
= – 2(7x + 12y)

Question 2.
The product of (23x²y³z) and (-15x³yz²) is __
(A) -34x⁵y⁴z³
(B) 34x²y³z⁵
(C) 145x³y²z
(D) 170x³y²z³
Solution:
(A) -34x⁵y⁴z³

Question 3.
Solve the following equations:
i. \(4 x+\frac{1}{2}=\frac{9}{2}\)
ii. 10 = 2y + 5
iii. 5m – 4 = 1
iv. 6x – 1 = 3x + 8
v. 2(x – 4) = 4x + 2
vi. 5(x + 1) = 74
Solution:
i. \(4 x+\frac{1}{2}=\frac{9}{2}\)

ii. 10 = 2y + 5

iii. 5m – 4 = 1

iv. 6x – 1 = 3x + 8

v. 2(x – 4) = 4x + 2

vi. 5(x + 1) = 74

Question 4.
Rakesh’s age is less than Sania’s age by 5 years. The sum of their ages is 27 years. How old are they?
Solution:
Let the age of Rakesh be x years.
∴ Sania’s age = (x + 5) years.
According to the given condition,
x + (x + 5) = 27
∴ 2x + 5 = 27
∴ 2x = 27 – 5
∴ 2x = 22
∴ \(x=\frac { 22 }{ 2 }=11\)
Sania’s age = x + 5 = 11 + 5 = 16 years
∴ The ages of Rakesh and Sania are 11 years and 16 years respectively.

Question 5.
When planting a forest, the number of jambhul trees planted was greater than the number of ashoka trees by 60. If there are altogether 200 trees of these two types, how many jambhul trees were planted?
Solution:
Let the number of jambhul trees planted be x.
∴ Number of ashoka trees = x – 60
According to the given condition, x + x – 60 = 200
∴ 2x = 200 + 60
∴ 2x = 260
∴ \(x=\frac { 260 }{ 2 }=130\)
∴ 130 jambhul trees were planted.

Question 6.
Shubhangi has twice as many 20-rupee notes as she has 50-rupee notes. Altogether, she has 2700 rupees. How many 50-rupee notes does she have?
Solution:
Let the number of 50-rupee notes with shubhangi be x.
∴ Number of 20-rupee notes = 2x
∴ Total amount with Shubhangi = Number of 50-rupee notes × 50 + Number of 20-rupee notes × 20
= x × 50 + 2x × 20
= 50x + 40x
= 90x
According to the given condition,
90x = 2700
∴ \(x=\frac { 2700 }{ 90 }=30\)
∴ Shubhangi has 30 notes of 50 rupees.

Question 7.
virat made twice as many runs as Rohit. The total of their scores is 2 less than a double century. How many runs did each of them make?
Solution:
Let the runs made by Rohit be x.
∴ Runs made by Virat = 2x
According to the given condition,
x + 2x = 200 – 2
∴ 3x = 198
∴ \(x=\frac { 198 }{ 3 }=66\)
∴ Runs made by Virat = 2x = 2 × 66 = 132
∴ The runs made by Virat and Rohit are 132 and 66 respectively.

Maharashtra Board Class 7 Maths Chapter 8 Algebraic Expressions and Operations on them Practice Set 36 Intext Questions and Activities

Question 1.
Solve the following equations. (Textbook pg. no. 59)
i. x + 7 = 4
ii. 4p = 12
iii. m – 5 = 4
iv. \(\frac { t }{ 3 }=6\)
Solution:
i. x + 7 = 4
∴ x + 7 – 7 = 4 – 7 ….(Subtracting 7 from both sides)
∴ x + 0 = -3
∴ x = -3

ii. 4p = 12
∴ \(\frac{4 p}{4}=\frac{12}{4}\) ….(Dividing both sides by 4)
∴ p = 3

iii. m – 5 = 4
∴ m – 5 + 5 = 4 + 5
…. (Adding 5 to both sides)
∴ m + 0 = 9
∴ m = 9

iv. \(\frac { t }{ 3 }=6\)
∴ \(\frac { t }{ 3 }\) × 3 = 6 × 3 …. (Multiplying both sides by 3)
∴ t = 18

Balbharti Maharashtra State Board Class 7 Maths Solutions covers the 7th Std Maths Practice Set 34 Answers Solutions Chapter 8 Algebraic Expressions and Operations on them.

Algebraic Expressions and Operations on them Class 7 Practice Set 34 Answers Solutions Chapter 8

Question 1.
Subtract the second expression from the first.
i. (4xy – 9z); (3xy – 16z)
ii. (5x + 4y + 7z); (x + 2y + 3z)
iii. (14x² + 8xy + 3y²); (26x² – 8xy – 17y²)
iv. (6x² + 7xy + 16y²); (16x² – 17xy)
v. (4x + 16z); (19y – 14z + 16x)
Solution:
i. (4xy – 9z) – (3xy – 16z)
= 4xy – 9z – 3xy + 16z
= (4xy – 3xy) + (16z – 9z)
= xy + 7z

ii. (5x + 4y + 7z) – (x + 2y + 3z)
= 5x + 4y + 7z – x – 2y – 3z
= (5x – x) + (4y – 2y) + (7z – 3z)
= 4x + 2y + 4z

iii. (14x² + 8xy + 3y²) – (26x² – 8xy – 17y²)
= 14x² + 8xy + 3y² – 26x² + 8xy + 17y²
= (14x² – 26x²) + (8xy + 8xy) + (3y² + 17y²)
= -12x² + 16xy + 20y²

iv. (6x² + 7xy + 16y²) – (16x² – 17xy)
= 6x² + 7xy + 16y² – 16x² + 17xy
= (6x² – 16x²) + (7xy + 17xy) + 16y²
= -10x² + 24xy + 16y²

v. (4x + 16z) – (19y— 14z + 16x)
= 4x + 16z – 19y + 14z – 16x
= (4x – 16x) – 19y + (16z + 14z)
= -12x – 19y + 30z

Balbharti Maharashtra State Board Class 7 Maths Solutions covers the 7th Std Maths Practice Set 32  Answers Solutions Chapter 8 Algebraic Expressions and Operations on them.

Algebraic Expressions and Operations on them Class 7 Practice Set 32 Answers Solutions Chapter 8

Question 1.
Classify the following algebraic expressions as monomials, binomials, trinomials or polynomials.
i. 7x
ii. 5y – 7z
iii. 3x³ – 5x² – 11
iv. 1 – 8a – 7a² – 7a³
v. 5m – 3
vi. a
vii. 4
viii. 3y² – 7y + 5
Solution:
i. Monomial
ii. Binomial
iii. Trinomial
iv. Polynomial
v. Binomial
vi. Monomial
vii. Monomial
viii. Trinomial