Class 10

Balbharti Maharashtra State Board Class 10 Maths Solutions covers the Practice Set 7.2 Geometry 10th Class Maths Part 2 Answers Solutions Chapter 7 Mensuration.

Practice Set 7.2 Geometry 10th Std Maths Part 2 Answers Chapter 7 Mensuration

Question 1.
The radii of two circular ends of frustum shaped bucket are 14 cm and 7 cm. Height of the bucket is 30 cm. How many litres of water it can hold? (1 litre = 1000 cm³)
Given: Radii (r₁) = 14 cm, and (r₂) = 7 cm,
height (h) = 30 cm
To find: Amount of water the bucket can hold.
Solution:
Volume of frustum = \(\frac { 1 }{ 3 } \) πh (r₁² + r₂² + r₁ × r₂)

∴ The bucket can hold 10.78 litres of water.

Question 2.
The radii of ends of a frustum are 14 cm and 6 cm respectively and its height is 6 cm. Find its
i. curved surface area,
ii. total surface area,
iii. volume, (π = 3.14)
Given: Radii (r₁) = 14 cm, and (r₂) = 6 cm,
height (h) = 6 cm
Solution:

i. Curved surface area of frustum
= πl (r₁ + r₂)
= 3.14 × 10(14 + 6)
= 3.14 × 10 × 20 = 628 cm²
∴ The curved surface area of the frustum is 628 cm².

ii. Total surface area of frustum
= πl (r₁+ r₂) + πr₁² + πr₂²
= 628 + 3.14 × (14)² + 3.14 × (6)²
= 628 + 3.14 × 196 + 3.14 × 36
= 628 + 3.14(196 + 36)
= 628 + 3.14 × 232
= 628 + 728.48
= 1356.48 cm²
∴ The total surface area of the frustum is 1356.48 cm².

iii. Volume of frustum
= \(\frac { 1 }{ 3 } \) πth(r₁² +r₂² + r₁ × r₂)
= \(\frac { 1 }{ 3 } \) × 3.14 × 6(14² + 6² + 14 × 6)
= 3.14 × 2(196 + 36 + 84)
= 3.14 × 2 × 316
= 1984.48 cm³
∴ The volume of the frustum is 1984.48 cm³.

Question 3.
The circumferences of circular faces of a frustum are 132 cm and 88 cm and its height is 24 cm. To find the curved surface area of frustum, complete the following activity. (π = \(\frac { 22 }{ 7 } \))
Solution:
Circumference1 = 27πr₁ = 132 cm

Curved surface area of frustum = π (r₁ + r₂) l
= π (21 + 14) × 25
=π × 35 × 35
= \(\frac { 22 }{ 7 } \) × 35 × 25
= 2750 cm²

Balbharti Maharashtra State Board Class 10 Maths Solutions covers the Practice Set 7.1  Geometry 10th Class Maths Part 2 Answers Solutions Chapter 7 Mensuration.

Practice Set 7.1 Geometry 10th Std Maths Part 2 Answers Chapter 7 Mensuration

Practice Set 7.1 Geometry 10th Question 1. Find the volume of a cone if the radius of its base is 1.5 cm and its perpendicular height is 5 cm.
Given: For the cone,
radius (r) = 1.5 cm,
perpendicular height (h) = 5 cm
To find: Volume of the cone.
Solution:
Volume of cone = \(\frac { 1 }{ 3 } \) πr²h

∴ The volume of the cone is 11.79 cm³.

Mensuration Practice Set 7.1 Question 2. Find the volume of a sphere of diameter 6 cm. [π = 3.14]
Given: For the sphere, diameter (d) = 6 cm
To find: Volume of the sphere.
Solution:
Radius (r) = \(\frac { d }{ 2 } \) = \(\frac { 6 }{ 2 } \) = 3 cm
Volume of sphere = \(\frac { 4 }{ 3 } \) πr²
= \(\frac { 4 }{ 3 } \) × 3.14 × (3)³
= 4 × 3.14 × 3 × 3
= 113.04 cm³
∴ The volume of the sphere is 113.04 cm³.

Practice Set 7.1 Geometry Class 10 Question 3. Find the total surface area of a cylinder if the radius of its base is 5 cm and height is 40 cm. [π = 3.14]
Given: For the cylinder,
radius (r) = 5 cm,
height (h) = 40 cm
To find: Total surface area of the cylinder.
Solution:
Total surface area of cylinder = 2πr (r + h)
= 2 × 3.14 × 5 (5 + 40)
= 2 × 3.14 × 5 × 45
= 1413 cm²
The total surface area of the cylinder is 1413 cm².

Practice Set 7.1 Geometry Question 4. Find the surface area of a sphere of radius 7 cm.
Given: For the sphere, radius (r) = 7 cm
To find: Surface area of the sphere.
Solution:
Surface area of sphere = Aπr²
= 4 × \(\frac { 22 }{ 7 } \) × (7)²
= 88 × 7
= 616 cm²
∴ The surface area of the sphere is 616 cm².

Practice Set 7.1 Question 5. The dimensions of a cuboid are 44 cm, 21 cm, 12 cm. It is melted and a cone of height 24 cm is made. Find the radius of its base.
Given: For the cuboid,
length (l) = 44 cm, breadth (b) = 21 cm,
height (h) = 12 cm
For the cone, height (H) = 24 cm
To find: Radius of base of the cone (r).
Solution:
Volume of cuboid = l × b × h
= 44 × 21 × 12 cm³
Volume of cone = \(\frac { 1 }{ 3 } \) πr²H
= \(\frac { 1 }{ 3 } \) × \(\frac { 22 }{ 7 } \) × r² × 24 cm³
Since the cuboid is melted to form a cone,
∴ volume of cuboid = volume of cone

∴ r² = 21 × 21
∴ r = 21 cm …[Taking square root of both sides]
∴ The radius of the base of the cone is 21 cm.

10th Class Geometry Practice Set 7.1 Question 6. Observe the measures of pots in the given figures. How many jugs of water can the cylindrical pot hold?

Given: For the conical water jug,
radius (r) = 3.5 cm, height (h) = 10 cm
For the cylindrical water pot,
radius (R) = 7 cm, height (H) = 10 cm
To find: Number of jugs of water the cylindrical pot can hold.
Solution:
Volume of conical jug = \(\frac { 1 }{ 3 } \) πr²h

∴ The cylindrical pot can hold 12 jugs of water.

Mensuration Class 10 Practice Set 7.1 Question 7. A cylinder and a cone have equal bases. The height of the cylinder is 3 cm and the area of its base is 100 cm². The cone is placed up on the cylinder. Volume of the solid figure so formed is 500 cm³. Find the total height of the figure

Given: For the cylindrical part,
height (h) = 3 cm,
area of the base (πr²)= 100 cm²
Volume of the entire figure = 500 cm³
To find: Total height of the figure.
Solution:
A cylinder and a cone have equal bases.
∴ they have equal radii.
radius of cylinder = radius of cone = r
Area of base = 100 cm²
∴ πr² =100 …(i)
Let the height of the conical part be H.
Volume of the entire figure
= Volume of the entire + Volume of cone

∴ Height of conical part (H) =6 cm
Total height of the figure = h + H
= 3 + 6
= 9 cm
∴ The total height of the figure is 9 cm.

10th Geometry Practice Set 7.1 Question 8. In the given figure, a toy made from a hemisphere, a cylinder and a cone is shown. Find the total area of the toy.

Given: For the conical Part,
height (h) = 4 cm, radius (r) = 3 cm
For the cylindrical part,
height (H) = 40 cm, radius (r) = 3 cm
For the hemispherical part,
radius (r) = 3 cm
To find: Total area of the toy.
Solution:
Slant height of cone (l) = \(\sqrt{\mathrm{h}^{2}+\mathrm{r}^{2}}\)
= \(\sqrt{\mathrm{4}^{2}+\mathrm{3}^{2}}\)
= \(\sqrt { 16+9 }\)
= \(\sqrt { 25 }\) = 5 cm
Curved surface area of cone = πrl
= π × 3 × 5
= 15π cm²
Curved surface area of cylinder = 2πrH
= 2 × π × 3 × 40
= 240π cm²
Curved surface area of hemisphere = 2πr²
= 2 × π × 3²
= 18π cm²
Total area of the toy
= Curved surface area of cone + Curved surface area of cylinder + Curved surface area of hemisphere
= 15π + 240π + 18π
= 2737 π cm²
∴ The total area of the toy is 273π cm².

7.1.8 Practice Question 9. In the given figure, a cylindrical wrapper of flat tablets is shown. The radius of a tablet is 7 mm and its thickness is 5 mm. How many such tablets are wrapped in the wrapper?

Given: For the cylindrical tablets,
radius (r) = 7 mm,
thickness = height(h) = 5 mm
For the cylindrical wrapper,
diameter (D) = 14 mm, height (H) = 10 cm
To find: Number of tablets that can be wrapped.
Solution:
Radius of wrapper (R) = \(\frac { Diameter }{ 2 } \)
= \(\frac { 14 }{ 2 } \) = 7 mm
Height of wrapper (H) = 10 cm
= 10 × 10 mm
= 100 mm
Volume of a cylindrical wrapper = πR²H
= π(7)² × 100
= 4900π mm³
Volume of a cylindrical tablet = πr²h
= π(7)² × 5
= 245 π mm³
No. of tablets that can be wrapped

∴ 20 tables can be wrapped in the wrapper

Class 10 Maths 7.1 Question 10. The given figure shows a toy. Its lower part is a hemisphere and the upper part is a cone. Find the volume and the surface area of the toy from the measures shown in the figure.
(π = 3.14)
Given: For the conical part,
height (h) = 4 cm, radius (r) = 3 cm
For the hemispherical part,
radius (r) = 3 cm
To find: Volume and surface area of the toy.
Solution:

Now, volume of the toy
= Volume of cone + volume of hemisphere
= 12π + 18π
= 30π
= 30 × 3.14
= 94.20 cm³
Also, surface area of the toy
= Curved surface area of cone + Curved surface area of hemisphere
= 15π + 18π
= 33π
= 33 × 3.14
= 103.62 cm²
∴ The volume and surface area of the toy are 94.20 cm³ and 103.62 cm² respectively.

Question 11.
Find the surface area and the volume of a beach ball shown in the figure.

Given: For the spherical ball,
diameter (d) = 42 cm
To find: Surface area and volume of the beach ball.
Solution:
Radius (r) = \(\frac { d }{ 2 } \) = \(\frac { 42 }{ 2 } \) = 21 cm
Surface area of sphere= 4πr²
= 4 × 3.14 × (21)²
= 4 × 3.14 × 21 × 21
= 5538.96 cm²
Volume of sphere = \(\frac { 4 }{ 3 } \) πr³
= \(\frac { 4 }{ 3 } \) × 3.14 × (21)³
= 4 × 3.14 × 7 × 21 × 21
= 38772.72 cm³
∴ The surface area and the volume of the beach ball are 5538.96 cm² and 38772.72 cm³ respectively.

Question 12.
As shown in the figure, a cylindrical glass contains water. A metal sphere of diameter 2 cm is immersed in it. Find the volume of the water.

Given: For the metal sphere,
diameter (d) = 2 cm
For the cylindrical glass, diameter (D) =14 cm,
height of water in the glass (H) = 30 cm
To find: Volume of water in the glass.
Solution:
Let the radii of the sphere and glass be r and R respectively.

Volume of water with sphere in it = πR²H
= π × (7)² × 30
= 1470π cm³
Volume of water in the glass
= Volume of water with sphere in it – Volume of sphere

∴ The volume of the water in the glass is 1468.67 π cm³ (i.e. 4615.80 cm³).

Maharashtra Board Class 10 Maths Chapter 7 Mensuration Intext Questions and Activities

Question 1.
The length, breadth and height of an oil can are 20 cm, 20 cm and 30 cm respectively as shown in the adjacent figure. How much oil will it contain? (1 litre = 1000 cm³) (Textbook pg. no.141)

Given: For the cuboidal can,
length (l) = 20 cm,
breadth (b) = 20 cm,
height (h) = 30 cm
To find: Oil that can be contained in the can.
Solution:
Volume of cuboid = l × b × h
= 20 × 20 × 30
= 12000 cm³
= \(\frac { 12000 }{ 1000 } \) litres
= 12 litres
∴ The oil can will contain 12 litres of oil.

Question 2.
The adjoining figure shows the measures of a Joker’s dap. How much cloth is needed to make such a cap? (Textbook pg. no. 141)

Given: For the conical cap,
radius (r) = 10 cm,
slant height (l) = 21 cm
To find: Cloth required to make the cap.
Solution:
Cloth required to make the cap
= Curved surface area of the conical cap
= πrl = \(\frac { 22 }{ 7 } \) × 10 × 21
=22 × 10 × 3
= 660 cm²
∴ 660 cm² of cloth will be required to make the cap.

Question 3.
As shown in the adjacent figure, a sphere is placed in a cylinder. It touches the top, bottom and the curved surface of the cylinder. If radius of the base of the cylinder is ‘r’,

i. what is the ratio of the radii of the sphere and the cylinder ?
ii. what is the ratio of the curved surface area of the cylinder and the surface area of the sphere?
iii. what is the ratio of the volumes of the cylinder and the sphere? (Textbook pg. no. 141)
Solution:
Radius of base of cylinder = radius of sphere
∴ Radius of sphere = r
Also, height of cylinder = diameter of sphere
∴ h = d
∴ h = 2r …(i)

∴ radius of sphere : radius of cylinder = 1 : 1.

∴ curved surface area of cylinder : surface area of sphere = 1:1.

∴ volume of cylinder : volume of sphere = 3 : 2.

Question 4.
Finding volume of a sphere using cylindrical beaker and water. (Textbook, pg. no. 142)

i. Take a ball and a beaker of the same radius.
ii. Cut a strip of paper of length equal to the diameter of the beaker.
iii. Draw two lines on the strip dividing it into three equal parts.
iv. Stick this strip on the beaker straight up from the bottom.
v. Fill the water in the beaker upto the first mark of the strip from bottom.
vi. Push the ball in the beaker so that it touches the bottom.
Observe how much water level rises.
You will notice that the water level has risen exactly upto the total height of the strip. Try to obtain the formula for volume of sphere using the volume of the cylindrical beaker.
Solution:
Suppose volume of beaker upto height 2r is V.
V = πr² h
∴ V = πr²(2r) …[∵ h = 2r]
∴ V = 2πr³
But, V = volume of the ball + volume of water in the beaker
∴ 2πr³ = Volume of the ball + \(\frac { 1 }{ 3 } \) × 2πr³
∴ Volume of the ball = 2πr³ – \(\frac { 2 }{ 3 } \) πr³
= \(\frac{6 \pi r^{3}-2 \pi r^{3}}{3}\)
∴ Volume of the ball = \(\frac { 4 }{ 3 } \) πr³
∴ Volume of a sphere = \(\frac { 4 }{ 3 } \) πr³

Balbharti Maharashtra State Board Class 10 Maths Solutions covers the Problem Set 6 Geometry 10th Class Maths Part 2 Answers Solutions Chapter 6 Trigonometry.

Problem Set 6 Geometry 10th Std Maths Part 2 Answers Chapter 6 Trigonometry

Question 1.
Choose the correct alternative answer for the following questions.

i. sin θ.cosec θ = ?
(A) 1
(B) 0
(C) \(\frac { 1 }{ 2 } \)
(D) \(\sqrt { 2 }\)
Answer:
(A)

ii. cosec 45° = ?
(A) \(\frac{1}{\sqrt{2}}\)
(B) \(\sqrt { 2 }\)
(C) \(\frac{\sqrt{3}}{2}\)
(D) \(\frac{1}{\sqrt{3}}\)
Answer:
(B)

iii. 1 + tan² θ = ?
(A) cot² θ
(B) cosec² θ
(C) sec² θ
(D) tan² θ
Answer:
(C)

iv. When we see at a higher level, from the horizontal line, angle formed is ______
(A) angle of elevation.
(B) angle of depression.
(C) 0
(D) straight angle.
Answer:
(A)

Question 2.
If sin θ = \(\frac { 11 }{ 61 } \), find the value of cos θ using trigonometric identity.
Solution:
sin θ = \(\frac { 11 }{ 61 } \) … [Given]
We know that,
sin² θ + cos² θ = 1


…[Taking square root of both sides]

Question 3.
If tan θ = 2, find the values of other trigonometric ratios.
Solution:
tan θ = 2 …[Given]
We know that,
1 + tan² θ = sec⁷ θ
∴ 1 + (2)⁷ = sec⁷ θ
∴ 1 + 4 = sec⁷ θ
∴ sec⁷ θ = 5
∴ sec θ = \(\sqrt { 5 }\) …[Taking square root of both sides]

Question 4.
If sec θ = \(\frac { 13 }{ 12 } \), find the values of other trigonometric ratios.
Solution:
sec θ = \(\frac { 13 }{ 12 } \) … [Given]
We know that,
1 + tan² θ = sec² θ


∴ sin θ = \(\frac { 5 }{ 13 } \), cos θ = \(\frac { 12 }{ 13 } \), tan θ = \(\frac { 5 }{ 12 } \), cot θ = \(\frac { 12 }{ 5 } \), cosec θ = \(\frac { 13 }{ 5 } \)

Question 5.
Prove the following:
i. sec θ (1 – sin θ) (sec θ + tan θ) = 1
ii. (sec θ + tan θ) (1 – sin θ) = cos θ
iii. sec² θ + cosec² θ = sec² θ × cosec² θ
iv. cot² θ – tan² θ = cosec² θ – sec² θ
v. tan⁴ θ + tan² θ = sec⁴ θ – sec² θ
vi. \(\frac{1}{1-\sin \theta}+\frac{1}{1+\sin \theta}\) = 2 sec2 θ
vii. sec⁶ x – tan⁶ x = 1 + 3 sec² x × tan² x

Proof:
i. L.H.S. = sec θ (1 – sin θ) (sec θ + tan θ)

∴ sec θ (1 – sin θ) (sec θ + tan θ) = 1

ii. L.H.S. = (sec θ + tan θ) (1 – sin θ)

∴ (sec θ + tan θ) (1 – sin θ) = cos θ

iii. L.H.S. = sec² θ + cosec² θ

∴ sec² θ + cosec² θ = sec² θ × cosec² θ

iv. L.H.S. = cot² θ – tan² θ
= (cosec² θ – 1) – (sec² θ – 1)
[∵ tan² θ = sec² θ – 1,
cot² θ = cosec² θ – 1]
= cosec² θ – 1 – sec² θ + 1
cosec² θ – sec² θ
= R.H.S.
∴ cot² θ – tan² θ = cosec² θ – sec² θ

v. L.H.S. = tan⁴ θ + tan² θ
= tan² θ (tan² θ + 1)
= tan² θ. sec² θ
…[∵ 1 + tan² θ = sec² θ]
= (sec² θ – 1) sec² θ
…[∵ tan² θ = sec² θ – 1]
= sec⁴ θ – sec² θ
= R.H.S.
∴ tan⁴ θ + tan² θ = sec⁴ θ – sec² θ

vii. L.H.S. = sec⁶ x – tan⁶ x
= (sec² x)³ – tan⁶ x
= (1 + tan² x)³ – tan⁶ x …[∵ 1 + tan² θ = sec² θ]
= 1 + 3tan² x + 3(tan² x)² + (tan² x)³ – tan⁶ x …[∵ (a + b)³ = a³ + 3a²b + 3ab² + b³]
= 1 + 3 tan² x (1 + tan² x) + tan⁶ x – tan⁶ x
= 1 + 3 tan² x sec² x …[∵ 1 + tan² θ = sec² θ]
= R.H.S.
∴ sec³x – tan⁶x = 1 + 3sec²x.tan²x


x. We know that,
sin² θ + cos² θ = 1
∴ 1 – sin² θ = cos² θ
∴ (1 – sin θ) (1 + sin θ) = cos θ. cos θ

Question 6.
A boy standing at a distance of 48 metres from a building observes the top of the building and makes an angle of elevation of 30°. Find the height of the building.
Solution:
Let AB represent the height of the building and point C represent the position of the boy.
Angle of elevation = ∠ACB = 30°
BC = 48 m

In right angled ∆ABC,
tan 30° = \(\frac { AB }{ BC } \) … [By definition]

∴ The height of the building is 16\(\sqrt { 3 }\) m.

Question 7.
From the top of the lighthouse, an observer looks at a ship and finds the angle of depression to be 30°. If the height of the lighthouse is 100 metres, then find how far the ship is from the lighthouse.
Solution:
Let AB represent the height of lighthouse and point C represent the position of the ship.

Angle of depression ∠PAC 30°
AB = 100m.
Now, ray AP || seg BC
∴ ∠ACB = ∠PAC … [Alternate angles]
∴ ∠ACB = 30°
AB = 100m
In right angled ∆ABC,
tan 30° = \(\frac { AB }{ BC } \) …[By definition]
∴ \(\frac{1}{\sqrt{3}}=\frac{100}{\mathrm{BC}}\)
∴ BC = 100\(\sqrt { 3 }\)m
∴ The ship is 1oo\(\sqrt { 3 }\)m far from the lighthouse.

Question 8.
Two buildings are in front of each other on a road of width 15 metres. From the top of the first building, having a height of 12 metre, the angle of elevation of the top of the second building is 30°. What is the height of the second building?
Solution:
Let AB and CD represent the heights of the two buildings, and BD represent the width of the road.

Draw seg AM ⊥ seg CD
Angle of elevation = ∠CAM = 30°
AB = 12m
BD = 15m
In ꠸ ABDM,
∠B = ∠D = 90°
∠M 90° …[segAM ⊥ segCD]
∠A 90° …[Remaining angle of ꠸ABDM]
꠸ABDM is a rectangle …[Each angle is 90°]

∴ The height of the second building is 20.65 m.

Question 9.
A ladder on the platform of a fire brigade van can be elevated at an angle of 70° to the maximum. The length of the ladder can be extended upto 20 m. If the platform is 2 m above the ground, find the maximum height from the ground upto which the ladder can reach. (sin 70° = 0.94)
Solution:
Let AB represent the length of the ladder and AE represent the height of the platform.

Draw seg AC ⊥ seg BD.
Angle of elevation = ∠BAC = 70°
AB = 20 m
AE = 2m
In right angled ∆ABC,
sin 70° = \(\frac { BC }{ AB } \) …..[By definition]
∴ 0.94 = \(\frac { BC }{ 20 } \)
∴ BC = 0.94 × 20
= 18.80 m
In ꠸ACDE,
∠E = ∠D = 90°
∠C = 90° … [seg AC ⊥ seg BD]
∴ ∠A = 90° … [Remaining angle of ꠸ACDE]
∴ ꠸ACDE is a rectangle. … [Each angle is 90°]
∴ CD = AE = 2 m … [Opposite sides of a rectangle]
Now, BD = BC + CD … [B – C – D]
= 18.80 + 2
= 20.80 m
∴ The maximum height from the ground upto which the ladder can reach is 20.80 metres.

Question 10.
While landing at an airport, a pilot made an angle of depression of 20°. Average speed of the plane was 200 km/hr. The plane reached the ground after 54 seconds. Find the height at which the plane was when it started landing, (sin 20° = 0.342)
Solution:
Let AC represent the initial height and point A represent the initial position of the plane.
Let point B represent the position where plane lands.
Angle of depression = ∠EAB = 20°

Now, seg AE || seg BC
∴ ∠ABC = ∠EAB … [Alternate angles]
∴ ∠ABC = 20°
Speed of the plane = 200 km/hr
= 200 × \(\frac { 1000 }{ 3600 } \) m/sec
= \(\frac { 500 }{ 9 } \) m/sec
∴ Distance travelled in 54 sec = speed × time
= \(\frac { 500 }{ 9 } \) × 54
= 3000 m
∴ AB = 3000 m
In right angled ∆ABC,
sin 20° = \(\frac { AC }{ AB } \) ….[By definition]
∴ 0.342 = \(\frac { AC }{ 3000 } \)
∴ AC = 0.342 × 3000
= 1026 m
∴ The plane was at a height of 1026 m when it started landing.

Balbharti Maharashtra State Board Class 10 Maths Solutions covers the Practice Set 5.3 Geometry 10th Class Maths Part 2 Answers Solutions Chapter 5 Co-ordinate Geometry.

Practice Set 5.3 Geometry 10th Std Maths Part 2 Answers Chapter 5 Co-ordinate Geometry

Practice Set 5.3 Geometry Class 10 Question 1. Angles made by the line with the positive direction of X-axis are given. Find the slope of these lines.
i. 45°
ii. 60°
iii. 90°
Solution:
i. Angle made with the positive direction of
X-axis (θ) = 45°
Slope of the line (m) = tan θ
∴ m = tan 45° = 1
∴ The slope of the line is 1.

ii. Angle made with the positive direction of X-axis (θ) = 60°
Slope of the line (m) = tan θ
∴ m = tan 60° = \(\sqrt { 3 }\)
∴ The slope of the line is \(\sqrt { 3 }\).

iii. Angle made with the positive direction of
X-axis (θ) = 90°
Slope of the line (m) = tan θ
∴ m = tan 90°
But, the value of tan 90° is not defined.
∴ The slope of the line cannot be determined.

Practice Set 5.3 Geometry Question 2. Find the slopes of the lines passing through the given points.
i. A (2, 3), B (4, 7)
ii. P(-3, 1), Q (5, -2)
iii. C (5, -2), D (7, 3)
iv. L (-2, -3), M (-6, -8)
v. E (-4, -2), F (6, 3)
vi. T (0, -3), s (0,4)
Solution:
i. A (x₁, y₁) = A (2, 3) and B (x₂, y₂) = B (4, 7)
Here, x₁ = 2, x₂ = 4, y₁ = 3, y₂ = 7

∴ The slope of line AB is 2.

ii. P (x₁, y₁) = P (-3, 1) and Q (x₂, y₂) = Q (5, -2)
Here, x₁ = -3, x₂ = 5, y₁ = 1, y₂ = -2

∴ The slope of line PQ is \(\frac { -3 }{ 8 } \)

iii. C (x₁, y₁) = C (5, -2) and D (x₂, y₂) = D (7, 3)
Here, x₁ = 5, x₂ = 7, y₁ = -2, y₂ = 3

∴ The slope of line CD is \(\frac { 5 }{ 2 } \)

iv. L (x₁, y₁) = L (-2, -3) and M (x₂,y₂) = M (-6, -8)
Here, x₁ = -2, x₂ = – 6, y₁ = – 3, y₂ = – 8

∴ The slope of line LM is \(\frac { 5 }{ 4 } \)

v. E (x₁, y₁) = E (-4, -2) and F (x₂, y₂) = F (6, 3)
Here,x₁ = -4, x₂ = 6, y₁ = -2, y₂ = 3

∴ The slope of line EF is \(\frac { 1 }{ 2 } \).

vi. T (x₁, y₁) = T (0, -3) and S (x₂, y₂) = S (0, 4)
Here, x₁ = 0, x₂ = 0, y₁ = -3, y₂ = 4

∴ The slope of line TS cannot be determined.

5.3.5 Practice Question 3. Determine whether the following points are collinear.
i. A (-1, -1), B (0, 1), C (1, 3)
ii. D (- 2, -3), E (1, 0), F (2, 1)
iii. L (2, 5), M (3, 3), N (5, 1)
iv. P (2, -5), Q (1, -3), R (-2, 3)
v. R (1, -4), S (-2, 2), T (-3,4)
vi. A(-4,4),K[-2,\(\frac { 5 }{ 2 } \)], N (4,-2)
Solution:


∴ slope of line AB = slope of line BC
∴ line AB || line BC
Also, point B is common to both the lines.
∴ Both lines are the same.
∴ Points A, B and C are collinear.

∴ slope of line DE = slope of line EF
∴ line DE || line EF
Also, point E is common to both the lines.
∴ Both lines are the same.
∴ Points D, E and F are collinear.

∴ slope of line LM ≠ slope of line MN
∴ Points L, M and N are not collinear.

∴ slope of line PQ = slope of line QR
∴ line PQ || line QR
Also, point Q is common to both the lines.
∴ Both lines are the same.
∴ Points P, Q and R are collinear.

∴ slope of line RS = slope of line ST
∴ line RS || line ST
Also, point S is common to both the lines.
∴ Both lines are the same.
∴ Points R, S and T are collinear.

∴ slope of line AK = slope of line KN
∴ line AK || line KN
Also, point K is common to both the lines.
∴ Both lines are the same.
∴ Points A, K and N are collinear.

Practice Set 5.3 Geometry 9th Standard Question 4. If A (1, -1), B (0,4), C (-5,3) are vertices of a triangle, then find the slope of each side.
Solution:

∴ The slopes of the sides AB, BC and AC are -5, \(\frac { 1 }{ 5 } \) and \(\frac { -2 }{ 3 } \) respectively.

Geometry 5.3 Question 5. Show that A (-4, -7), B (-1, 2), C (8, 5) and D (5, -4) are the vertices of a parallelogram.
Proof:


∴ Slope of side AB = Slope of side CD … [From (i) and (iii)]
∴ side AB || side CD
Slope of side BC = Slope of side AD … [From (ii) and (iv)]
∴ side BC || side AD
Both the pairs of opposite sides of ꠸ABCD are parallel.
꠸ABCD is a parallelogram.
Points A(-4, -7), B(-1, 2), C(8, 5) and D(5, -4) are the vertices of a parallelogram.

Question 6.
Find k, if R (1, -1), S (-2, k) and slope of line RS is -2.
Solution:
R(x₁, y₁) = R (1, -1), S (x₂, y₂) = S (-2, k)
Here, x₁ = 1, x₂ = -2, y₁ = -1, y₂ = k

But, slope of line RS is -2. … [Given]
∴ -2 = \(\frac { k+1 }{ -3 } \)
∴ k + 1 = 6
∴ k = 6 – 1
∴ k = 5

5.3 Class 10 Question 7. Find k, if B (k, -5), C (1, 2) and slope of the line is 7.
Solution:
B(x₁, y₁) = B (k, -5), C (x₂, y₂) = C (1, 2)
Here, x₁ = k, x₂ = 1, y₁ = -5, y₂ = 2

But, slope of line BC is 7. …[Given]
∴ 7 = \(\frac { 7 }{ 1-k } \)
∴ 7(1 – k) = 7
∴ 1 – k = \(\frac { 7 }{ 7 } \)
∴ 1 – k = 1
∴ k = 0

Question 8.
Find k, if PQ || RS and P (2, 4), Q (3, 6), R (3,1), S (5, k).
Solution:

But, line PQ || line RS … [Given]
∴ Slope of line PQ = Slope of line RS
∴ 2 = \(\frac { k-1 }{ 2 } \)
∴ 4 = k – 1
∴ k = 4 + 1
∴ k = 5

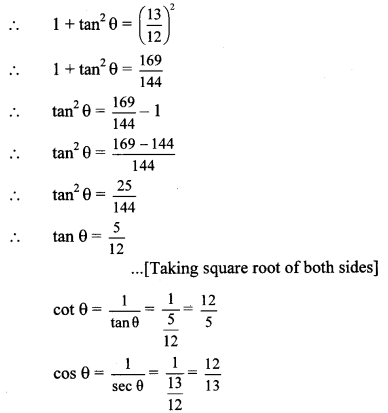
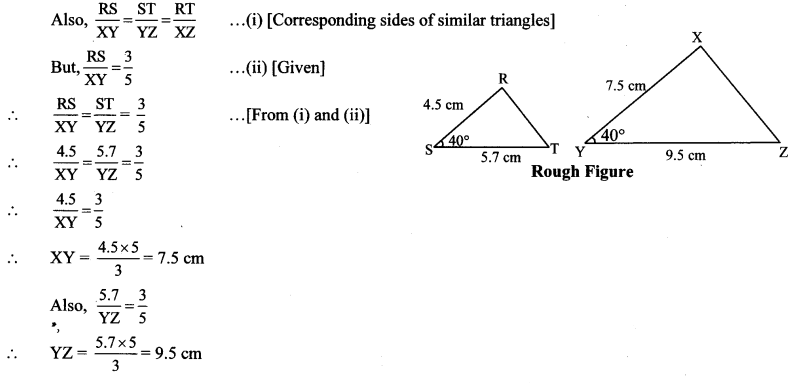
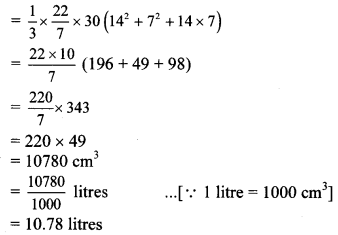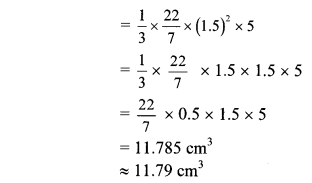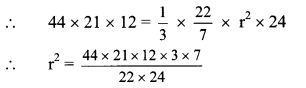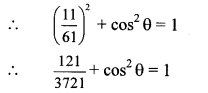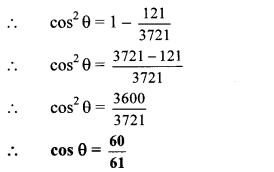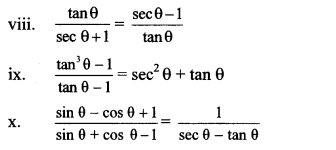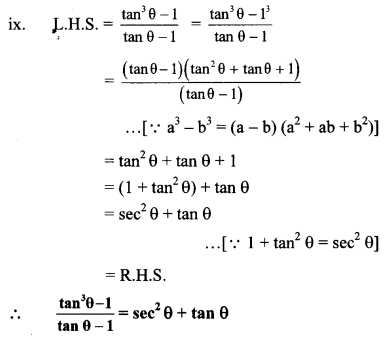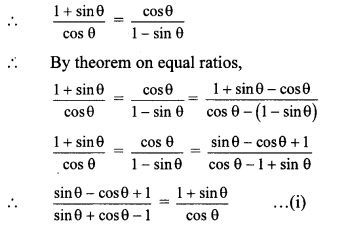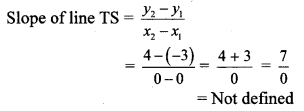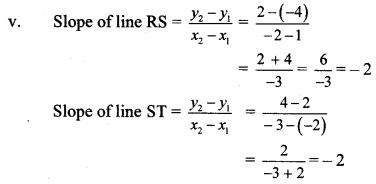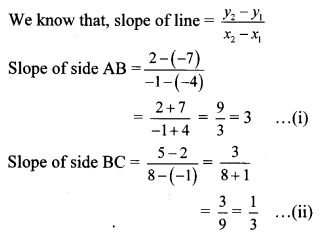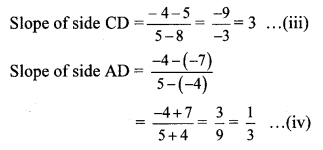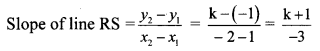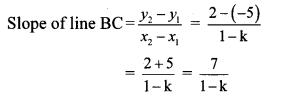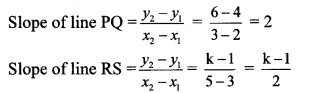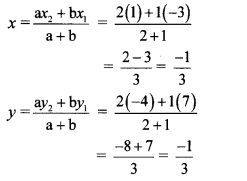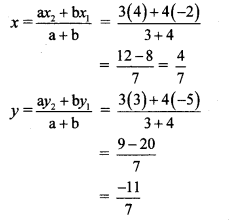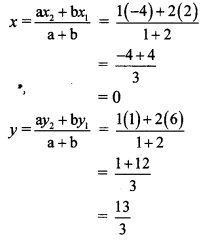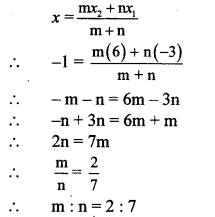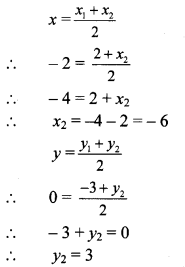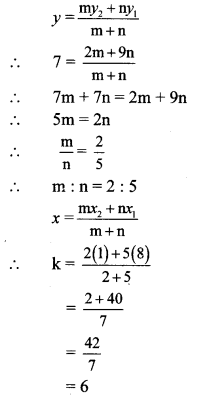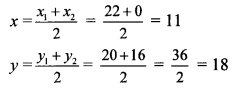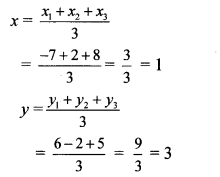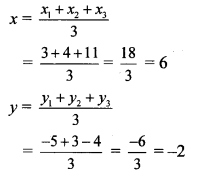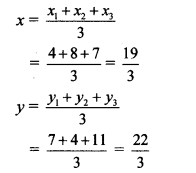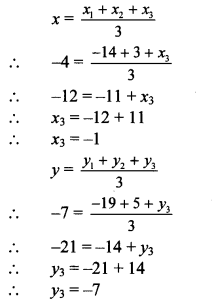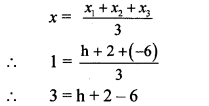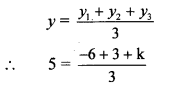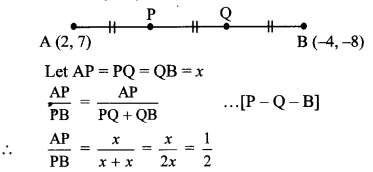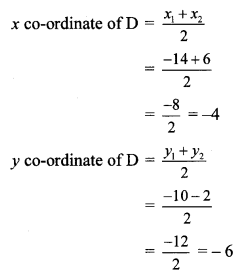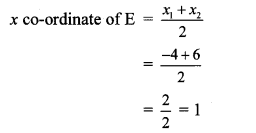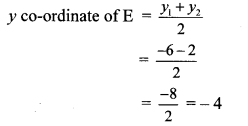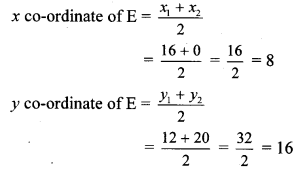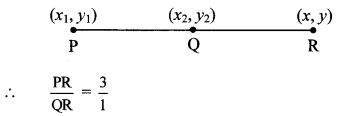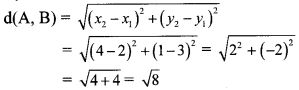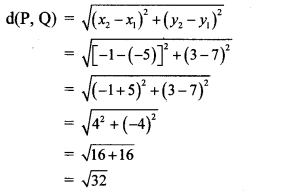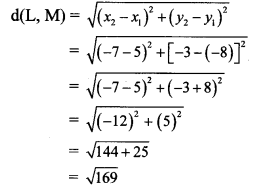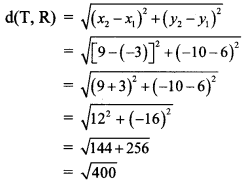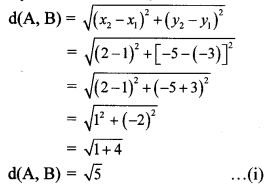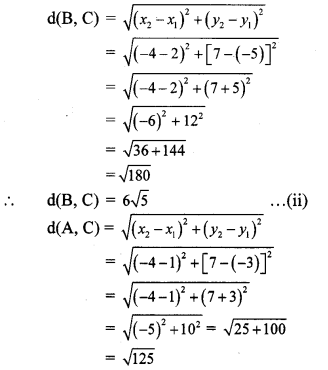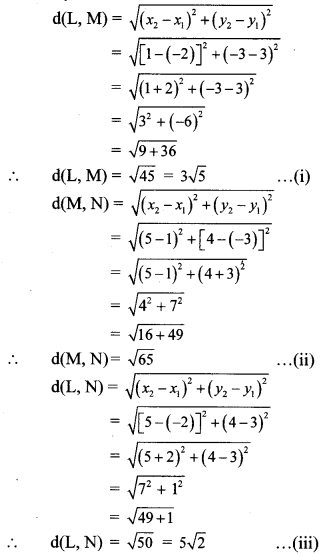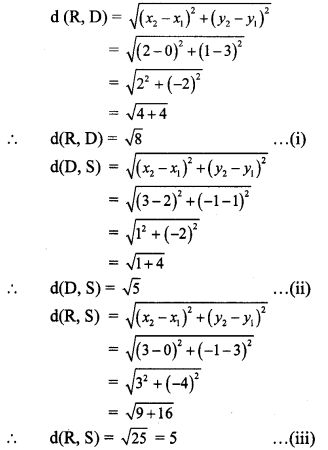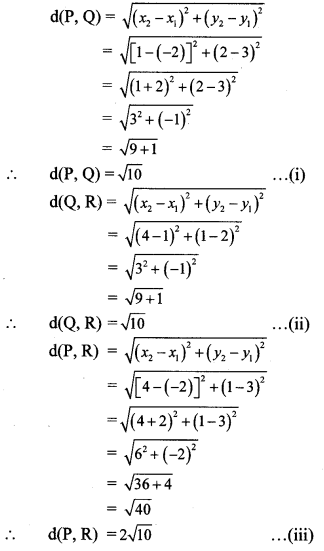Balbharti Maharashtra State Board Class 10 Maths Solutions covers the Practice Set 5.2 Geometry 10th Class Maths Part 2 Answers Solutions Chapter 5 Co-ordinate Geometry.

Practice Set 5.2 Geometry 10th Std Maths Part 2 Answers Chapter 5 Co-ordinate Geometry

Question 1.
Find the co-ordinates of point P if P divides the line segment joining the points A (-1, 7) and B (4, -3) in the ratio 2:3.
Solution:
Let the co-ordinates of point P be (x, y) and A (x₁, y₁) B (x₂, y₂) be the given points.
Here, x₁ = -1, y₁ = 7, x₂ = 4, y₂ = -3, m = 2, n = 3
∴ By section formula,

∴ The co-ordinates of point P are (1,3).

Question 2.
In each of the following examples find the co-ordinates of point A which divides segment PQ in the ratio a : b.
i. P (-3, 7), Q (1, -4), a : b = 2 : 1
ii. P (-2, -5), Q (4, 3), a : b = 3 : 4
iii. P (2, 6), Q (-4, 1), a : b = 1 : 2
Solution:
Let the co-ordinates of point A be (x, y).
i. Let P (x₁, y₁), Q (x₂, y₂) be the given points.
Here, x₁ = -3, y₁ = 7, x₂ = 1, y₂ = -4, a = 2, b = 1
∴ By section formula,

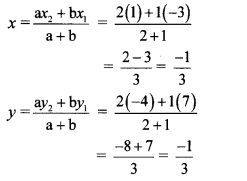
∴ The co-ordinates of point A are (\(\frac { -1 }{ 3 } \),\(\frac { -1 }{ 3 } \)).

ii. Let P (x₁,y₁), Q (x₂, y₂) be the given points.
Here, x₁ = -2, y₁ = -5, x₂ = 4, y₂ = 3, a = 3, b = 4
By section formula,

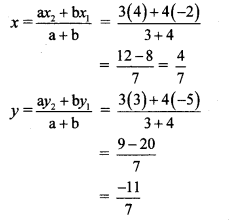
∴ The co-ordinates of point A are (\(\frac { 4 }{ 7 } \),\(\frac { -11 }{ 7 } \))

iii. Let P (x₁, y₁), Q (x₂, y₂) be the given points.
Here,x₁ = 2,y₁ = 6, x₂ = -4, y₂ = 1, a = 1,b = 2
∴ By section formula,

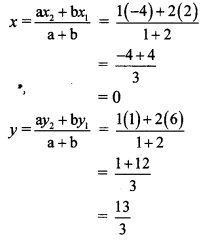
∴ The co-ordinates of point A are (0,\(\frac { 13 }{ 3 } \))

Question 3.
Find the ratio in which point T (-1, 6) divides the line segment joining the points P (-3,10) and Q (6, -8).
Solution:
Let P (x₁, y₁), Q (x₂, y₂) and T (x, y) be the given points.
Here, x₁ = -3, y₁ = 10, x₂ = 6, y₂ = -8, x = -1, y = 6
∴ By section formula,

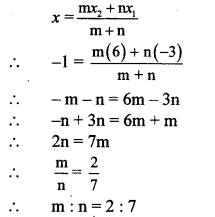
∴ Point T divides seg PQ in the ratio 2 : 7.

Question 4.
Point P is the centre of the circle and AB is a diameter. Find the co-ordinates of point B if co-ordinates of point A and P are (2, -3) and (-2,0) respectively.
Solution:
Let A (x₁, y₁), B (x₂, y₂) and P (x, y) be the given points.
Here, x₁ = 2, y₁ =-3,
x = -2, y = 0

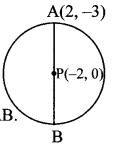
Point P is the midpoint of seg AB.
∴ By midpoint formula,

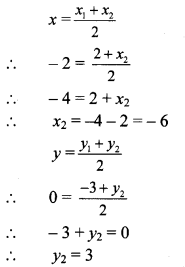
∴ The co-ordinates of point B are (-6,3).

Question 5.
Find the ratio in which point P (k, 7) divides the segment joining A (8, 9) and B (1,2). Also find k.
Solution:
Let A (x₁, y₁), B (x₂, y₂) and P (x, y) be the given points.
Here, x₁ = 8, y₁ = 9, x₂ = 1, y₂ = 2, x = k, y = 7
∴ By section formula,

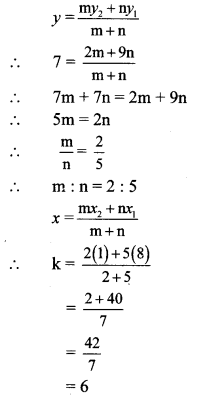
∴ Point P divides seg AB in the ratio 2 : 5, and the value of k is 6.

Question 6.
Find the co-ordinates of midpoint of the segment joining the points (22, 20) and (0,16).
Solution:
Let A (x₁, y₁) = A (22, 20),
B (x₂,y₂) = B (0, 16)
Let the co-ordinates of the midpoint be P (x,y).
∴ By midpoint formula,

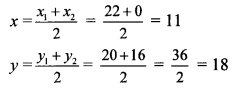
The co-ordinates of the midpoint of the segment joining (22, 20) and (0, 16) are (11,18).

Question 7.
Find the centroids of the triangles whose vertices are given below.
i. (-7, 6), (2,-2), (8, 5)
ii. (3, -5), (4, 3), (11,-4)
iii. (4, 7), (8, 4), (7, 11)
Solution:
i. Let A (x₁, y₁) = A (-7, 6),
B (x₂, y₂) = B (2, -2),
C (x₃, y₃) = C(8, 5)
∴ By centroid formula,

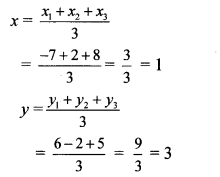
∴ The co-ordinates of the centroid are (1,3).

ii. Let A (x₁ y₁) = A (3, -5),
B (x₂, y₂) = B (4, 3),
C(x₃, y₃) = C(11,-4)
∴ By centroid formula,

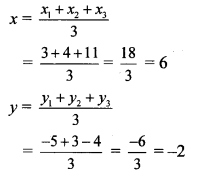
∴ The co-ordinates of the centroid are (6, -2).

iii. Let A (x₁, y₁) = A (4, 7),
B (x₂, y₂) = B (8,4),
C (x₃, y₃) = C(7,11)
∴ By centroid formula,

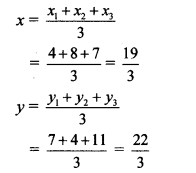
∴ The co-ordinates of the centroid are (\(\frac { 19 }{ 3 } \),\(\frac { 22 }{ 3 } \))

Question 8.
In ∆ABC, G (-4, -7) is the centroid. If A (-14, -19) and B (3, 5), then find the co-ordinates of C.
Solution:
G (x, y) = G (-4, -7),
A (x₁, y₁) = A (-14, -19),
B(x₂, y₂) = B(3,5)
Let the co-ordinates of point C be (x₃, y₃).
G is the centroid.
By centroid formula,

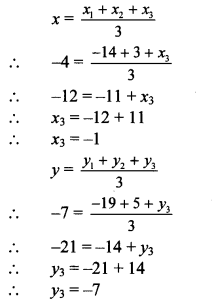
∴ The co-ordinates of point C are (-1, – 7).

Question 9.
A (h, -6), B (2, 3) and C (-6, k) are the co-ordinates of vertices of a triangle whose centroid is G (1,5). Find h and k.
Solution:
A(x₁,y₁) = A(h, -6),
B (x₂, y₂) = B(2, 3),
C (x₃, y₃) = C (-6, k)
∴ centroid G (x, y) = G (1, 5)
G is the centroid.
By centroid formula,

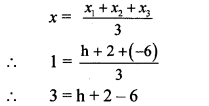
∴ 3 = h – 4
∴ h = 3 + 4
∴ h = 7

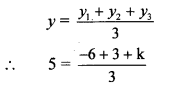
∴ 15 = -3 + k
∴ k = 15 + 3
∴ k = 18
∴ h = 7 and k = 18

Question 10.
Find the co-ordinates of the points of trisection of the line segment AB with A (2,7) and B (-4, -8).
Solution:
A (2, 7), B H,-8)
Suppose the points P and Q trisect seg AB.
∴ AP = PQ = QB

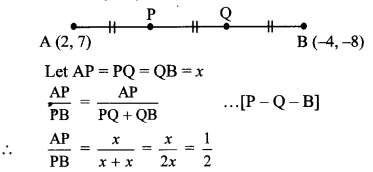
∴ Point P divides seg AB in the ratio 1:2.
∴ By section formula,

Co-ordinates of P are (0, 2).
Point Q is the midpoint of PB.
By midpoint formula,

Co-ordinates of Q are (-2, -3).
∴ The co-ordinates of the points of trisection seg AB are (0,2) and (-2, -3).

Question 11.
If A (-14, -10), B (6, -2) are given, find the co-ordinates of the points which divide segment AB into four equal parts.
Solution:
Let the points C, D and E divide seg AB in four equal parts.

Point D is the midpoint of seg AB.
∴ By midpoint formula,

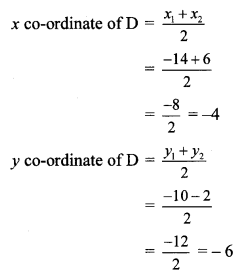
∴ Co-ordinates of D are (-4, -6).
Point C is the midpoint of seg AD.
∴ By midpoint formula,

∴ Co-ordinates of C are (-9, -8).
Point E is the midpoint of seg DB.
∴ By midpoint formula,


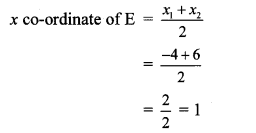
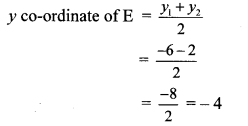
∴ Co-ordinates of E are (1,-4).
∴ The co-ordinates of the points dividing seg AB in four equal parts are C(-9, -8), D(-4, -6) and E(1, – 4).

Question 12.
If A (20, 10), B (0, 20) are given, find the co-ordinates of the points which divide segment AB into five congruent parts.
Solution:
Suppose the points C, D, E and F divide seg AB in five congruent parts.
∴ AC = CD = DE = EF = FB

∴ co-ordinates of C are (16, 12).
E is the midpoint of seg CB.
By midpoint formula,

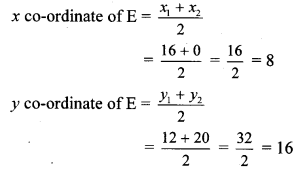
∴ co-ordinates of E are (8, 16).
D is the midpoint of seg CE.

∴ co-ordinates of F are (4, 18).
∴ The co-ordinates of the points dividing seg AB in five congruent parts are C (16, 12), D (12, 14), E (8, 16) and F (4, 18).

Maharashtra Board Class 10 Maths Chapter 5 Co-ordinate Geometry Intext Questions and Activities

Question 1.
A (15, 5), B (9, 20) and A-P-B. Find the ratio in which point P (11, 15) divides segment AB. Find the ratio using x and y co-ordinates. Write the conclusion. (Textbook pg. no. 113)
Solution:
Suppose point P (11,15) divides segment AB in the ratio m : n.
By section formula,

∴ Point P divides seg AB in the ratio 2 : 1.
The ratio obtained by using x and y co-ordinates is the same.

Question 2.
External division: (Textbook pg. no. 115)
Suppose point R divides seg PQ externally in the ratio 3:1.

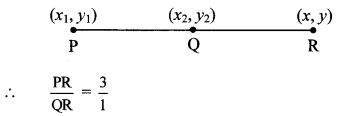
Let the common multiple be k.
Let PR = 3k and QR = k
Now, PR = PQ + QR … [P – Q – R]
∴ 3k = PQ + k
∴ \(\frac { PQ }{ QR } \) = \(\frac { 2k }{ k } \) = \(\frac { 2 }{ 1 } \)
∴ Point Q divides seg PR in the ratio 2 : 1 internally.
Thus, we can find the co-ordinates of point R, when co-ordinates of points P and Q are given.

Balbharti Maharashtra State Board Class 10 Maths Solutions covers the Practice Set 6.2 Geometry 10th Class Maths Part 2 Answers Solutions Chapter 6 Trigonometry.

Practice Set 6.2 Geometry 10th Std Maths Part 2 Answers Chapter 6 Trigonometry

Question 1.
A person is standing at a distance of 80 m from a church looking at its top. The angle of elevation is of 45°. Find the height of the church.
Solution:
Let AB represent the height of the church and point C represent the position of the person.

BC = 80 m
Angle of elevation = ∠ACB = 45°
In right angled ∆ABC,
tan 45° = \(\frac { AB }{ BC } \) … [By definition]
∴ 1 = \(\frac { AB }{ 80 } \)
∴ AB = 80m
∴ The height of the church is 80 m.

Question 2.
From the top of a lighthouse, an observer looking at a ship makes angle of depression of 60°. If the height of the lighthouse is 90 metre, then find how far the ship is from the lighthouse. ( \(\sqrt { 3 }\) = 1.73)
Solution:
Let AB represent the height of lighthouse and point C represent the position of the ship.
AB = 90 m

Angle of depression = ∠PAC = 60°
Now, ray AP || seg BC
∴ ∠ACB = ∠PAC … [Alternate angles]
∴ ∠ACB = 60°
In right angled ∆ABC,
tan 60° = \(\frac { AB }{ BC } \) … [By definition]

∴ The ship is 51.90 m away from the lighthouse.

Question 3.
Two buildings are facing each other on a road of width 12 metre. From the top of the first building, which is 10 metre high, the angle of elevation of the top of the second is found to be 60°. What is the height of the second building?
Solution:
Let AB and CD represent the heights of the two buildings, and BD represent the width of the road.

Draw seg AM ⊥ seg CD.
Angle of elevation = ∠CAM = 60°
AB = 10 m
BD= 12 m
In ꠸ABDM,
∠B = ∠D = 90°
∠M = 90° … [seg AM ⊥ seg CD]
∴ ∠A = 90° … [Remaining angle of ꠸ABDM]
∴ ꠸ABDM is a rectangle …. [Each angle is 90°]
∴ AM = BD = 12 m opposite sides
DM = AB = 10 m of a rectangle
In right angled ∆AMC,
tan 60° = \(\frac { CM }{ AM } \) …[By definition]
∴ \(\sqrt { 3 }\) = \(\frac { CM }{ 12 } \)
∴ CM = 12\(\sqrt { 3 }\) m
Now, CD = DM + CM … [C – M – D]
∴ CD = (10 + 12\(\sqrt { 3 }\))m
= 10 + 12 × 1.73
= 10 + 20.76 = 30.76
∴ The height of the second building is 30.76 m.

Question 4.
Two poles of heights 18 metre and 7 metre are erected on a ground. The length of the wire fastened at their tops is 22 metre. Find the angle made by the wire with the horizontal.
Solution:
Let AB and CD represent the heights of two poles, and AC represent the length of the wire.

Draw seg AM ⊥ seg CD.
Angle of elevation = ∠CAM = θ
AB = 7 m
CD = 18 m
AC = 22 m
In ꠸ABDM,
∠B = ∠D = 90°
∠M = 90° …[seg AM ⊥ seg CD]
∴ ∠A = 90° … [Remaining angle of ꠸ABDM]
∴ □ABDM is a rectangle. … [Each angle is 90°]
∴ DM = AB = 7 m … [Opposite sides of a rectangle]
Now, CD = CM + DM … [C – M – D]
∴ 18 = CM + 7
∴ CM = 18 – 7 = 11 m
In right angled ∆AMC,
sin θ = \(\frac { CM }{ AC } \) …..[By definition]
∴ sin θ = \(\frac { 11 }{ 22 } \) = \(\frac { 1 }{ 2 } \)
But, sin 30° = \(\frac { 1 }{ 2 } \)
∴ θ = 30°
∴ The angle made by the wire with the horizontal is 30°.

Question 5.
A storm broke a tree and the treetop rested 20 m from the base of the tree, making an angle of 60° with the horizontal. Find the height of the tree.
Solution:
Let AB represent the height of the tree.
Suppose the tree broke at point C and its top touches the ground at D.
AC is the broken part of the tree which takes position CD such that ∠CDB = 60°
∴ AC = CD …(i)
BD = 20 m
In right angled ∆CBD,

tan 60° = \(\frac { BC }{ BD } \) … [By definition]
∴ \(\sqrt { 3 }\) = \(\frac { BC }{ 20 } \)
∴ BC = 20\(\sqrt { 3 }\) m
Also, cos 60° = \(\frac { BC }{ CD } \) … [By definition]
∴ \(\frac { 1 }{ 2 } \) = \(\frac { 20 }{ CD } \)
∴ CD = 20 × 2 = 40 m
∴ AC = 40 m …[From(i)]
Now, AB = AC + BC ….[A – C – B]
= 40 + 20\(\sqrt { 3 }\)
= 40 + 20 × 1.73
= 40 + 34.6
= 74.6
∴ The height of the tree is 74.6 m.

Question 6.
A kite is flying at a height of 60 m above the ground. The string attached to the kite is tied at the ground. It makes an angle of 60° with the ground. Assuming that the string is straight, find the length of the string. (\(\sqrt { 3 }\) = 1.73)
Solution:
Let AB represent the height at which kite is flying and point C represent the point where the string is tied at the ground.
∠ACB is the angle made by the string with the ground.

∠ACB = 60°
AB = 60 m
In right angled ∆ABC,
sin 60° = \(\frac { AB }{ AC } \) … [By definition]

∴ AC = 40 \(\sqrt { 3 }\) = 40 × 1.73 = 69.20 m
∴ The length of the string is 69.20 m.

Balbharti Maharashtra State Board Class 10 Maths Solutions covers the Practice Set 5.1 Geometry 10th Class Maths Part 2 Answers Solutions Chapter 5 Co-ordinate Geometry.

Practice Set 5.1 Geometry 10th Std Maths Part 2 Answers Chapter 5 Co-ordinate Geometry

Practice Set 5.1 Geometry Class 10 Question 1. Find the distance between each of the following pairs of points.
i. A (2, 3), B (4,1)
ii. P (-5, 7), Q (-1, 3)
iii. R (0, -3), S (0,\(\frac { 5 }{ 2 } \))
iv. L (5, -8), M (-7, -3)
v. T (-3, 6), R (9, -10)
vi. W(\(\frac { -7 }{ 2 } \),4), X(11, 4)
Solution:
i. Let A (x₁, y₁) and B (x₂, y₂) be the given points.
∴ x₁ = 2, y₁ = 3, x₂ = 4, y₂ = 1
By distance formula,

∴ d(A, B) = 2\(\sqrt { 2 }\) units
∴ The distance between the points A and B is 2\(\sqrt { 2 }\) units.

ii. Let P (x₁, y₁ ) and Q (x₂, y₂) be the given points.
∴ x₁ = -5, y₁ = 7, x₂ = -1, y₂ = 3
By distance formula,

∴ d(P, Q) = 4\(\sqrt { 2 }\) units
∴ The distance between the points P and Q is 4\(\sqrt { 2 }\) units.

iii. Let R (x₁, y₁) and S (x₂, y₂) be the given points.
∴ x₁ = 0, y₁ = -3, x₂ = 0, y₂ = \(\frac { 5 }{ 2 } \)
By distance formula,

∴ d(R, S) = \(\frac { 11 }{ 2 } \) units
∴ The distance between the points R and S is \(\frac { 11 }{ 2 } \) units.

iv. Let L (x₁, y₁) and M (x₂, y₂) be the given points.
∴ x₁ = 5, y₁ = -8, x₂ = -7, y₂ = -3
By distance formula,

∴ d(L, M) = 13 units
∴ The distance between the points L and M is 13 units.

v. Let T (x₁,y₁) and R (x₂, y₂) be the given points.
∴ x₁ = -3, y₁ = 6,x₂ = 9,y₂ = -10
By distance formula,

∴ d(T, R) = 20 units
∴ The distance between the points T and R 20 units.

vi. Let W (x₁, y₁) and X (x₂, y₂) be the given points.

∴ d(W, X) = \(\frac { 29 }{ 2 } \) units
∴ The distance between the points W and X is \(\frac { 29 }{ 2 } \) units.

Practice Set 5.1 Geometry 10th Question 2. Determine whether the points are collinear.
i. A (1, -3), B (2, -5), C (-4, 7)
ii. L (-2, 3), M (1, -3), N (5, 4)
iii. R (0, 3), D (2, 1), S (3, -1)
iv. P (-2, 3), Q (1, 2), R (4, 1)
Solution:
i. By distance formula,


∴ d(A, B) = \(\sqrt { 5 }\) …(i)
On adding (i) and (iii),
d(A, B) + d(A, C)= \(\sqrt { 5 }\) + 5\(\sqrt { 5 }\) = 6\(\sqrt { 5 }\)
∴ d(A, B) + d(A, C) = d(B, C) … [From (ii)]
∴ Points A, B and C are collinear.

ii. By distance formula,

On adding (i) and (iii),
d(L, M) + d(L, N) = 3\(\sqrt { 5 }\) + 5\(\sqrt { 2 }\) ≠ \(\sqrt { 65 }\)
∴ d(L, M) + d(L, N) ≠ d(M, N) … [From (ii)]
∴ Points L, M and N are not collinear.

iii. By distance formula,

On adding (i) and (ii),
∴ d(R, D) + d(D, S) = \(\sqrt { 8 }\) + \(\sqrt { 5 }\) ≠ 5
∴ d(R, D) + d(D, S) ≠ d(R, S) … [From (iii)]
∴ Points R, D and S are not collinear.

iv. By distance formula,

On adding (i) and (ii),
d(P, Q) + d(Q, R) = \(\sqrt { 10 }\) + \(\sqrt { 10 }\) = 2\(\sqrt { 10 }\)
∴ d(P, Q) + d(Q, R) = d(P, R) … [From (iii)]
∴ Points P, Q and R are collinear.

Coordinate Geometry Class 10 Practice Set 5.1 Question 3. Find the point on the X-axis which is equidistant from A (-3,4) and B (1, -4).
Solution:
Let point C be on the X-axis which is equidistant from points A and B.
Point C lies on X-axis.
∴ its y co-ordinate is 0.
Let C = (x, 0)
C is equidistant from points A and B.
∴ AC = BC

∴ (x + 3)² + (-4)² = (x- 1)² + 4²
∴ x² + 6x + 9 + 16 = x² – 2x + 1 + 16
∴ 8x = – 8
∴ x = – \(\frac { 8 }{ 8 } \) = -1
∴ The point on X-axis which is equidistant from points A and B is (-1,0).

10th Geometry Practice Set 5.1 Question 4. Verify that points P (-2, 2), Q (2, 2) and R (2, 7) are vertices of a right angled triangle.
Solution:
Distance between two points

Consider, PQ² + QR² = 42 + 52 = 16 + 25 = 41 … [From (i) and (ii)]
∴ PR² = PQ² + QR² … [From (iii)]
∴ ∆PQR is a right angled triangle. … [Converse of Pythagoras theorem]
∴ Points P, Q and R are the vertices of a right angled triangle.

Question 5.
Show that points P (2, -2), Q (7, 3), R (11, -1) and S (6, -6) are vertices of a parallelogram.
Proof:
Distance between two points

PQ = RS … [From (i) and (iii)]
QR = PS … [From (ii) and (iv)]
A quadrilateral is a parallelogram, if both the pairs of its opposite sides are congruent.
∴ □ PQRS is a parallelogram.
∴ Points P, Q, R and S are the vertices of a parallelogram.

Question 6.
Show that points A (-4, -7), B (-1, 2), C (8, 5) and D (5, -4) are vertices of rhombus ABCD.
Proof:
Distance between two points


∴ AB = BC = CD = AD …[From (i), (ii), (iii) and (iv)]
In a quadrilateral, if all the sides are equal, then it is a rhombus.
∴ □ ABCD is a rhombus.
∴ Points A, B, C and D are the vertices of rhombus ABCD.

Practice Set 5.1 Question 7. Find x if distance between points L (x, 7) and M (1,15) is 10.
Solution:
X₁ = x, y₁ = 7, x₂ = 1, y₂ = 15
By distance formula,

∴ 1 – x = ± 6
∴ 1 – x = 6 or l – x = -6
∴ x = – 5 or x = 7
∴ The value of x is – 5 or 7.

Geometry 5.1 Question 8. Show that the points A (1, 2), B (1, 6), C (1 + 2\(\sqrt { 3 }\), 4) are vertices of an equilateral triangle.
Proof:
Distance between two points

∴ AB = BC = AC … [From (i), (ii) and (iii)]
∴ ∆ABC is an equilateral triangle.
∴ Points A, B and C are the vertices of an equilateral triangle.

Maharashtra Board Class 10 Maths Chapter 5 Coordinate Geometry Intext Questions and Activities

Question 1.
In the figure, seg AB || Y-axis and seg CB || X-axis. Co-ordinates of points A and C are given. To find AC, fill in the boxes given below. (Textbook pa. no. 102)

Solution:
In ∆ABC, ∠B = 900
∴ (AB)² + (BC)² = [(Ac)² …(i) … [Pythagoras theorem]
seg CB || X-axis
∴ y co-ordinate of B = 2
seg BA || Y-axis
∴ x co-ordinate of B = 2
∴ co-ordinate of B is (2, 2) = (x₁,y₁)
co-ordinate of A is (2, 3) = (x₂, Y₂)
Since, AB || to Y-axis,
d(A, B) = Y₂ – Y₁
d(A,B) = 3 – 2 = 1
co-ordinate of C is (-2,2) = (x₁,y₁)
co-ordinate of B is (2, 2) = (x₂, y₂)
Since, BC || to X-axis,
d(B, C) = x₂ – x₁
d(B,C) = 2 – -2 = 4
∴ AC² = 12 + 42 …[From (i)]
= 1 + 16 = 17
∴ AC = \(\sqrt { 17 }\) units …[Taking square root of both sides]

Balbharti Maharashtra State Board Class 10 Maths Solutions covers the Problem Set 4 Geometry 10th Class Maths Part 2 Answers Solutions Chapter 4 Geometric Constructions.

Problem Set 4 Geometry 10th Std Maths Part 2 Answers Chapter 4 Geometric Constructions

Question 1.
Select the correct alternative for each of the following questions.

i. The number of tangents that can be drawn to a circle at a point on the circle is ______
(A) 3
(B) 2
(C) 1
(D) 0
Answer:
(C)

ii. The maximum number of tangents that can be drawn to a circle from a point outside it is ______
(A) 2
(B) 1
(C) one and only one
(D) 0
Answer:
(A)

iii. If ∆ABC ~ ∆PQR and \(\frac { AB }{ PQ } \) = \(\frac { 7 }{ 5 } \), then ______
(A) AABC is bigger.
(B) APQR is bigger.
(C) both triangles will be equal
(D) can not be decided
Answer:
(A)

Question 2.
Draw a circle with centre O and radius 3.5 cm. Take point P at a distance 5.7 cm from the centre. Draw tangents to the circle from point P.
Solution:
Analysis:
As shown in the figure, let P be a point in the exterior of circle at a distance of 5.7 cm.
Let PQ and PR be the tangents to the circle at points Q and R respectively.
∴ seg OQ ⊥ tangent PQ …[Tangent is perpendicular to radius]
∴ ∠OQP = 90°

∴ point Q is on the circle having OP as diameter. …[Angle inscribed in a semicircle is a right angle]
Similarly, point R also lies on the circle having OP as diameter.
∴ Points Q and R lie on the circle with OP as diameter.
On drawing a circle with OP as diameter, the points where it intersects the circle with centre O, will be the positions of points Q and R respectively.

Question 3.
Draw any circle. Take any point A on it and construct tangent at A without using the centre of the circle.
Solution:
Analysis:
As shown in the figure, line l is a tangent to the circle at point A.
seg BA is a chord of the circle and ∠BCA is an inscribed angle.
By tangent secant angle theorem,
∠BCA = ∠BAR

By converse of tangent secant angle theorem,
If we draw ∠BAR such that ∠BAR = ∠BCA, then ray AR (i.e. line l) is a tangent at point A.

Question 4.
Draw a circle of diameter 6.4 cm. Take a point R at a distance equal to its diameter from the centre. Draw tangents from point R.
Solution:
Diameter of circle = 6.4 cm 6.4
Radius of circle = \(\frac { 6.4 }{ 2 } \) = 3.2 cm
Analysis:
As shown in the figure, let R be a point in the exterior of circle at a distance of 6.4 cm.
Let RQ and RS be the tangents to the circle at points Q and S respectively.

∴ seg PQ ⊥tangent RQ …[Tangent is perpendicular to radius]
∴ ∠PQR = 90°
∴ point Q is on the circle having PR as diameter. …[Angle inscribed in a semicircle is a right angle]
Similarly,
Point S also lies on the circle having PR as diameter.
∴ Points Q and S lie on the circle with PR as diameter.
On drawing a circle with PR as diameter, the points where it intersects the circle with centre P, will be the positions of points Q and S respectively.

Question 5.
Draw a circle with centre P. Draw an arc AB of 100° measure. Draw tangents to the circle at point A and point B.
Solution:
m(arc AB) = ∠APB = 100°
Analysis:
seg PA ⊥ line l
seg PB ⊥line m … [Tangent is perpendicular to radius]

The perpendicular to seg PA and seg PB at points A and B respectively will give the required tangents at A and B.

Steps of construction:
i. With centre P, draw a circle of any radius and take any point A on it.
ii. Draw ray PA.
iii. Draw ray PB such that ∠APB = 100°.
iv. Draw line l ⊥ray PA at point A.
v. Draw line m ⊥ ray PB at point B.
Lines l and m are tangents at points A and B to the circle.

Question 6.
Draw a circle of radius 3.4 cm and centre E. Take a point F on the circle. Take another point A such that E – F – A and FA = 4.1 cm. Draw tangents to the circle from point A.
Solution:
Analysis:
Draw a circle of radius 3.4 cm
As shown in the figure, let A be a point in the exterior of circle at a distance of (3.4 + 4.1) = 7.5 cm.
Let AP and AQ be the tangents to the circle at points P and Q respectively.
∴ seg EP ⊥ tangent PA … [Tangent is perpendicular to radius]

∴ ∠EPA = 90°
∴ point P is on the circle having EA as diameter. …[Angle inscribed in a semicircle is a right angle]
Similarly, point Q also lies on the circle having EA as diameter.
∴ Points P and Q lie on the circle with EA as diameter.
On drawing a circle with EA as diameter, the points where it intersects the circle with centre E, will be the positions of points P and Q respectively.

Question 7.
∆ABC ~ ∆LBN. In ∆ABC, AB = 5.1 cm, ∠B = 40°, BC = 4.8 cm, \(\frac { AC }{ LN } \) = \(\frac { 4 }{ 7 } \). Construct ∆ABC and ∆LBN.
Solution:
Analysis:
As shown in the figure,
Let B – C – N and B – A – L.

∆ABC ~ ∆LBN …[Given]
∴ ∠ABC ≅ ∠LBN …[Corresponding angles of similar triangles]
\(\frac { AB }{ LB } \) = \(\frac { BC }{ BN } \) = \(\frac { AC }{ LN } \) …(i)[Corresponding sides of similar triangles]
But. \(\frac { AC }{ LN } \) = \(\frac { 4 }{ 7 } \) …(ii)[Given]
∴ \(\frac { AB }{ LB } \) = \(\frac { BC }{ BN } \) = \(\frac { AC }{ LN } \) = \(\frac { 4 }{ 7 } \) …[From(i)and(ii)]
∴ sides of ∆LBN are longer than corresponding sides of ∆ABC.
∴ If seg BC is divided into 4 equal parts, then seg BN will be 7 times each part of seg BC.
So, if we construct ∆ABC, point N will be on side BC, at a distance equal to 7 parts from B.
Now, point L is the point of intersection of ray BA and a line through N, parallel to AC.
∆LBN is the required triangle similar to ∆ABC.

Steps of construction:
i. Draw ∆ABC of given measure. Draw ray BD making an acute angle with side BC.
ii. Taking convenient distance on compass, mark 7 points B₁, B₂, B₃, B₄, B₅, B₆ and B₇ such that
BB₁ = B₁B₂ = B₂B₃ B₃= B4₄ = B₄B₅ = B₅B₆ = B₆B₇.
iii. Join B₄C. Draw line parallel to B₄C through B₇ to intersects ray BC at N.
iv. Draw a line parallel to side AC through N. Name the point of intersection of this line and ray BA as L.
∆LBN is the required triangle similar to ∆ABC.

Question 8.
Construct ∆PYQ such that, PY = 6.3 cm, YQ = 7.2 cm, PQ = 5.8 cm. If = \(\frac { YZ }{ YQ } \) = \(\frac { 6 }{ 5 } \) then construct ∆XYZ similar to ∆PYQ.
Solution:

Analysis:
As shown in the figure,
Let Y – Q – Z and Y – P – X.
∆XYZ ~ ∆PYQ …[Given]
∴ ∠XYZ ≅ ∠PYQ …[Corresponding angles of similar triangles]
\(\frac { XY }{ PY } \) = \(\frac { YZ }{ YQ } \) = \(\frac { XZ }{ PQ } \) …(i)[Corresponding sides of similar triangles]
But, \(\frac { YZ }{ YQ } \) = \(\frac { 6 }{ 5 } \) ,..(ii)[Given]
∴ \(\frac { XY }{ PY } \) = \(\frac { YZ }{ YQ } \) = \(\frac { XZ }{ PQ } \) = \(\frac { 6 }{ 5 } \) …[From (i) and (ii)]
∴ sides of ∆XYZ are longer than corresponding sides of ∆PYQ.
∴ If seg YQ is divided into 5 equal parts, then seg YZ will be 6 times each part of seg YQ.
So, if we construct ∆PYQ, point Z will be on side YQ, at a distance equal to 6 parts from Y.
Now, point X is the point of intersection of ray YP and a line through Z, parallel to PQ.
∆XYZ is the required triangle similar to ∆PYQ.

Steps of construction:
i. Draw ∆ PYQ of given measure. Draw ray YT making an acute angle with side YQ.
ii. Taking convenient distance on compass, mark 6 points Y₁, Y₂, Y₃, Y₄, Y₅ and Y₆ such that
YY₁ = Y₁Y₂ = Y₂Y₃ = Y₃Y₄ = Y₄Y₅ = Y₅Y₆.
iii. Join Y₅Q. Draw line parallel to Y₅Q through Y₆ to intersects ray YQ at Z.
iv. Draw a line parallel to side PQ through Z. Name the point of intersection of this line and ray YP as X.
∆XYZ is the required triangle similar to ∆PYQ.

Balbharti Maharashtra State Board Class 10 Maths Solutions covers the Practice Set 4.2 Geometry 10th Class Maths Part 2 Answers Solutions Chapter 4 Geometric Constructions.

Practice Set 4.2 Geometry 10th Std Maths Part 2 Answers Chapter 4 Geometric Constructions

Question 1.
Construct a tangent to a circle with centre P and radius 3.2 cm at any point M on it.
Solution:
Analysis:
seg PM ⊥ line l ….[Tangent is perpendicular to radius]

The perpendicular to seg PM at point M will give the required tangent at M.

Question 2.
Draw a circle of radius 2.7 cm. Draw a tangent to the circle at any point on it.
Solution:
Analysis:
seg OM ⊥ line l …[Tangent is perpendicular to radius]

The perpendicular to seg OM at point M will give the required tangent at M.

Question 3.
Draw a circle of radius 3.6 cm. Draw a tangent to the circle at any point on it without using the centre.
Solution:
Analysis:
As shown in the figure, line lis a tangent to the circle at point K.
seg BK is a chord of the circle and LBAK is an inscribed angle.
By tangent secant angle theorem,
∠BAK = ∠BKR

By converse of tangent secant angle theorem,
If we draw ∠BKR such that ∠BKR = ∠BAK, then ray KR
i.e. (line l) is a tangent at point K.

Question 4.
Draw a circle of radius 3.3 cm. Draw a chord PQ of length 6.6 cm. Draw tangents to the circle at points P and Q. Write your observation about the tangents.
Solution:
Analysis:
seg OP ⊥ line l …[Tangent is perpendicular to radius]
seg OQ ⊥ line m

The perpendicular to seg OP and seg OQ at points P and Q
respectively will give the required tangents at P and Q.

Radius = 3.3 cm
∴ Diameter = 2 × 3.3 = 6.6 cm
∴ Chord PQ is the diameter of the circle.
∴ The tangents through points P and Q (endpoints of diameter) are parallel to each other.

Question 5.
Draw a circle with radius 3.4 cm. Draw a chord MN of length 5.7 cm in it. Construct tangents at points M and N to the circle.
Solution:
Analysis:
seg ON ⊥ linel l
seg OM ⊥ Iine m …….[Tangent is perpendicular to radius]

The perpendicular to seg ON and seg 0M at points N and M respectively will give the required tangents at N and M.

Question 6.
Draw a circle with centre P and radius 3.4 cm. Take point Q at a distance 5.5 cm from the centre. Construct tangents to the circle from point Q.
Solution:
Analysis:
As shown in the figure, let Q be a point in the exterior of circle at a distance of 5.5 cm.
Let QR and QS be the tangents to the circle at points R and S respectively.

∴ seg PR ⊥ tangent QR …[Tangent is perpendicular to radius]
∴ ∠PRQ = 90°
∴ point R is on the circle having PQ as diameter. …[Angle inscribed in a semicircle is a right angle]
Similarly, point S also lies on the circle having PQ as diameter.
∴ Points R and S lie on the circle with PQ as diameter.
On drawing a circle with PQ as diameter, the points where it intersects the circle with centre P, will be the positions of points R and S respectively.
Ray QR and QS are the required tangents to the circle from point Q.

Question 7.
Draw a circle with radius 4.1 cm. Construct tangents to the circle from a point at a distance 7.3 cm from the centre.
Solution:
Analysis:
As shown in the figure, let Q be a point in the exterior of circle at a distance of 5.5 cm.
Let QR and QS be the tangents to the circle at points R and S respectively.
∴ seg PR ⊥ tangent QR …[Tangent is perpendicular to radius]
∴ ∠PRQ = 90°

∴ point R is on the circle having PQ as diameter. …[Angle inscribed in a semicircle is a right angle]
Similarly, point S also lies on the circle having PQ as diameter.
∴ Points R and S lie on the circle with PQ as diameter.
On drawing a circle with PQ as diameter, the points where it intersects the circle with centre P, will be the positions of points R and S respectively.
Ray QR and QS are the required tangents to the circle from point Q.

Balbharti Maharashtra State Board Class 10 Maths Solutions covers the Practice Set 4.1 Geometry 10th Class Maths Part 2 Answers Solutions Chapter 4 Geometric Constructions.

Practice Set 4.1 Geometry 10th Std Maths Part 2 Answers Chapter 4 Geometric Constructions

Question 1.
∆ABC ~ ∆LMN. In ∆ABC, AB = 5.5 cm, BC = 6 cm, CA = 4.5 cm. Construct ∆ABC and ∆LMN such that \(\frac { BC }{ MN } \) = \(\frac { 5 }{ 4 } \)
Solution:
Analysis:

Question 2.
∆PQR ~ ∆LTR. In ∆PQR, PQ = 4.2 cm, QR = 5.4 cm, PR = 4.8 cm. Construct ∆PQR and ∆LTR, such that \(\frac { PQ }{ LT } \) = \(\frac { 3 }{ 4 } \)
Solution:
Analysis:
As shown in the figure, Let R – P – L and R – Q – T.
∆PQR ~ ∆LTR … [Given]
∴ ∠PRQ ≅ ∠LRT … [Corresponding angles of similar triangles]

\(\frac { PQ }{ LT } \) = \(\frac { QR }{ TR } \) = \(\frac { PR }{ LR } \) …(i)[Corresponding sides of similar triangles]
But, \(\frac { PQ }{ LT } \) = \(\frac { 3 }{ 4 } \) ….(ii) [Given]
∴ \(\frac { PQ }{ LT } \) = \(\frac { QR }{ TR } \) = \(\frac { PR }{ LR } \) = \(\frac { 3 }{ 4 } \) …[From (i) and (ii)]
∴ sides of LTR are longer than corresponding sides of ∆PQR.
If seg QR is divided into 3 equal parts, then seg TR will be 4 times each part of seg QR.
So, if we construct ∆PQR, point T will be on side RQ, at a distance equal to 4 parts from R.
Now, point L is the point of intersection of ray RP and a line through T, parallel to PQ.
∆LTR is the required triangle similar to ∆PQR.

Steps of construction:
i. Draw ∆PQR of given measure. Draw ray RS making an acute angle with side RQ.
ii. Taking convenient distance on the compass, mark 4 points R₁, R₂, R₃, and R₄, such that RR₁ = R₁R₂ = R₂R₃ = R₃R₄.
iii. Join R₃Q. Draw line parallel to R₃Q through R₄ to intersects ray RQ at T.
iv. Draw a line parallel to side PQ through T. Name the point of intersection of this line and ray RP as L.
∆LTR is the required triangle similar to ∆PQR.

Question 3.
∆RST ~ ∆XYZ. In ∆RST, RS = 4.5 cm, ∠RST = 40°, ST = 5.7 cm. Construct ∆RST and ∆XYZ, such that \(\frac { RS }{ XY } \) = \(\frac { 3 }{ 5 } \).
Solution:
Analysis:
∆RST ~ ∆XYZ … [Given]
∴ ∠RST ≅ ∠XYZ = 40° … [Corresponding angles of similar triangles]

Question 4.
∆AMT ~ ∆ANE. In ∆AMT, AM = 6.3 cm, ∠TAM = 500, AT = 5.6 cm. \(\frac { AM }{ AH } \) = \(\frac { 7 }{ 5 } \) Construct ∆AHE.
Solution:
Analysis:
As shown in the figure,
Let A – H – M and A – E – T.
∆AMT ~ ∆AHE … [Given]
∴ ∠TAM ≅ ∠EAH … [Corresponding angles of similar triangles]

\(\frac { AM }{ AH } \) = \(\frac { MT }{ HE } \) = \(\frac { AT }{ AE } \) ….. (i)[Corresponding sides of similar triangles]
But, \(\frac { AM }{ AH } \) = \(\frac { 7 }{ 5 } \) …(ii)[Given]
∴ \(\frac { AM }{ AH } \) = \(\frac { MT }{ HE } \) = \(\frac { AT }{ AH } \) = \(\frac { 7 }{ 5 } \) …[From (i) and (ii)]
∴ Sides of AAMT are longer than corresponding sides of ∆AHE.
∴ The length of side AH will be equal to 5 parts out of 7 equal parts of side AM.
So, if we construct AAMT, point H will be on side AM, at a distance equal to 5 parts from A.
Now, point E is the point of intersection of ray AT and a line through H, parallel to MT.
∆AHE is the required triangle similar to ∆AMT.

Steps of construction:
i. Draw ∆AMT of given measure. Draw ray AB making an acute angle with side AM.
ii. Taking convenient distance on the compass, mark 7 points A1, A2, A3, A4, A5, Ag and A7, such that
AA₁ = A₁A₂ = A₂A₃ = A₃A₄ = A₄A₅ = A₅A₆ = A₆A₇.
iii. Join A₇M. Draw line parallel to A₇M through A₅ to intersects seg AM at H.
iv. Draw a line parallel to side TM through H. Name the point of intersection of this line and seg AT as E.
∆AHE is the required triangle similar to ∆AMT.

Maharashtra Board Class 10 Maths Chapter 4 Geometric Constructions Intext Questions and Activities

Question 1.
If length of side AB is \(\frac { 11.6 }{ 2 } \) cm, then by dividing the line segment of length 11.6 cm in three equal parts, draw segment AB. (Textbook pg. no. 93)
Solution:

Steps of construction:
i. Draw seg AD of 11.6 cm.
ii. Draw ray AX such that ∠DAX is an acute angle.
iii. Locate points A₁, A₂ and A₃ on ray AX such that AA₁ = A₁A₂ = A₂A₃
iv. Join A₃D.
v. Through A₁, A₂ draw lines parallel to A₃D intersecting AD at B and C, wherein
AB = \(\frac { 11.6 }{ 3 } \) cm

Question 2.
Construct any ∆ABC. Construct ∆ A’BC’ such that AB : A’B = 5:3 and ∆ ABC ~ ∆ A’BC’. (Textbook pg. no. 93)
Analysis:
As shown in the figure,
Let B – A’ – A and B – C’ -C
∆ ABC – A’BC’ … [Given]
∴ ∠ABC ≅ ∠A’BC’ …[Corresponding angles of similar trianglesi


∴ Sides of ∆ABC are longer than corresponding sides of ∆A’BC’. Rough figure
∴ the length of side BC’ will be equal to 3 parts out of 5 equal parts of side BC.
So if we construct ∆ABC, point C’ will be on side BC, at a distance equal to 3 parts from B.
Now A’ is the point of intersection of AB and a line through C’, parallel to CA.
Solution:
Let ∆ABC be any triangle constructed such that AB = 7 cm, BC = 7 cm and AC = 6 cm.

Question 3.
Construct any ∆ABC. Construct ∆A’BC’ such that AB: A’B = 5:3 and ∆ABC ~ ∆A’BC’.
∆A’BC’ can also be constructed as shown in the adjoining figure. What changes do we have to make in steps of construction in that case? (Textbook pg. no. 94)

Solution:
Let ∆ABC be any triangle constructed such that AB = 5cm,
BC = 5.5 cm and AC = 6 cm.

i. Steps of construction:
Construct ∆ABC, extend rays AB and CB.
Draw line BM making an acute angle with side AB.
Mark 5 points B₁, B₂, B₃, B₄, B₅ starting from B at equal distance.
Join B₃C” (ie 3rd part)
Draw a line parallel to AB₅ through B₃ to intersect line AB at C”
Draw a line parallel to AC through C” to intersect line BC at A”
ii. Extra construction:
With radius BC” cut an arc on extended ray CB at C’ [C’ – B – C]
With radius BA” cut an arc on extended ray AB at A’ [A’ – B – A]
∆A’BC’ is the required triangle.