Prasanna

Balbharti Maharashtra State Board Class 9 Maths Solutions covers the Practice Set 2.3 Algebra 9th Class Maths Part 1 Answers Solutions Chapter 2 Real Numbers.

Practice Set 2.3 Algebra 9th Std Maths Part 1 Answers Chapter 2 Real Numbers

Question 1.
State the order of the surds given below.

Answer:
i. 3, ii. 2, iii. 4, iv. 2, v. 3

Question 2.
State which of the following are surds Justify. [2 Marks each]

Answer:
i. \(\sqrt [ 3 ]{ 51 }\) is a surd because 51 is a positive rational number, 3 is a positive integer greater than 1 and \(\sqrt [ 3 ]{ 51 }\) is irrational.

ii. \(\sqrt [ 4 ]{ 16 }\) is not a surd because

= 2, which is not an irrational number.

iii. \(\sqrt [ 5 ]{ 81 }\) is a surd because 81 is a positive rational number, 5 is a positive integer greater than 1 and \(\sqrt [ 5 ]{ 81 }\) is irrational.

iv. \(\sqrt { 256 }\) is not a surd because

= 16, which is not an irrational number.

v. \(\sqrt [ 3 ]{ 64 }\) is not a surd because

= 4, which is not an irrational number.

vi. \(\sqrt { \frac { 22 }{ 7 } }\) is a surd because \(\frac { 22 }{ 7 }\) is a positive rational number, 2 is a positive integer greater than 1 and \(\sqrt { \frac { 22 }{ 7 } }\) is irrational.

Question 3.
Classify the given pair of surds into like surds and unlike surds. [2 Marks each]

Solution:
If the order of the surds and the radicands are same, then the surds are like surds.

Here, the order of 2\(\sqrt { 13 }\) and 5\(\sqrt { 13 }\) is same and their radicands are also same.
∴ \(\sqrt { 52 }\) and 5\(\sqrt { 13 }\) are like surds.

Here, the order of 2\(\sqrt { 17 }\) and 5\(\sqrt { 3 }\) is same but their radicands are not.
∴ \(\sqrt { 68 }\) and 5\(\sqrt { 3 }\) are unlike surds.

Here, the order of 12\(\sqrt { 2 }\) and 7\(\sqrt { 2 }\) is same and their radicands are also same.
∴ 4\(\sqrt { 18 }\) and 7\(\sqrt { 2 }\) are like surds.

Here, the order of 38\(\sqrt { 3 }\) and 6\(\sqrt { 3 }\) is same and their radicands are also same.
∴ 19\(\sqrt { 12 }\) and 6\(\sqrt { 3 }\) are like surds.

v. 5\(\sqrt { 22 }\), 7\(\sqrt { 33 }\)
Here, the order of 5\(\sqrt { 22 }\) and 7\(\sqrt { 33 }\) is same but their radicands are not.
∴ 5\(\sqrt { 22 }\) and 7\(\sqrt { 33 }\) are unlike surds.

Here, the order of 5√5 and 5√3 is same but their radicands are not.
∴ 5√5 and √75 are unlike surds.

Question 4.
Simplify the following surds.

Solution:

Question 5.
Compare the following pair of surds.


Solution:

Question 6.
Simplify.

Solution:

Question 7.
Multiply and write the answer in the simplest form.

Solution:

Question 8.
Divide and write form.

Solution:

Question 9.
Rationalize the denominator.

Solution:

Question 1.
\(\sqrt { 9+16 }\) ? + \(\sqrt { 9 }\) + \(\sqrt { 16 }\) (Texbookpg. no. 28)
Solution:

Question 2.
\(\sqrt { 100+36 }\) ? \(\sqrt { 100 }\) + \(\sqrt { 36 }\) (Textbook pg. no. 28)
Solution:

Question 3.
Follow the arrows and complete the chart by doing the operations given. (Textbook pg. no. 34)

Solution:

Question 4.
There are some real numbers written on a card sheet. Use these numbers and construct two examples each of addition, subtraction, multiplication and division. Solve these examples. (Textbook pg. no. 34)

Solution:

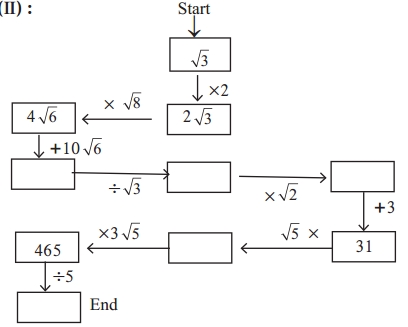
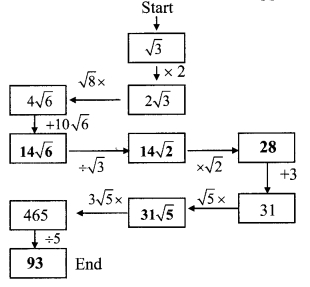
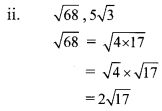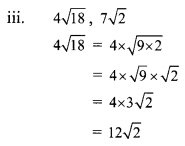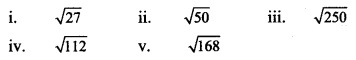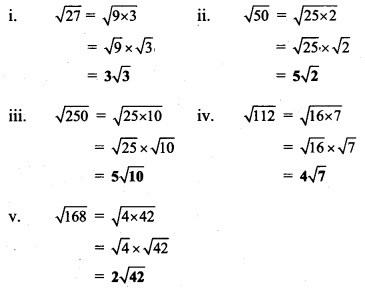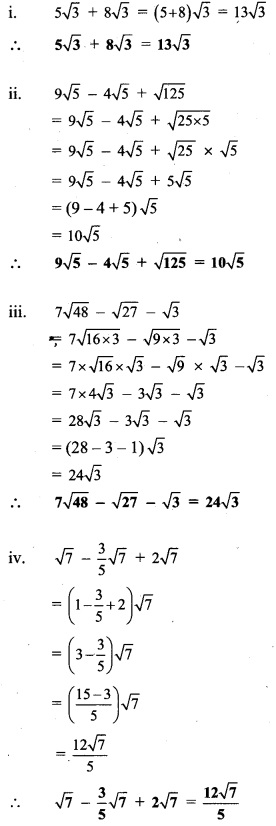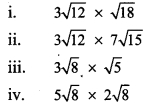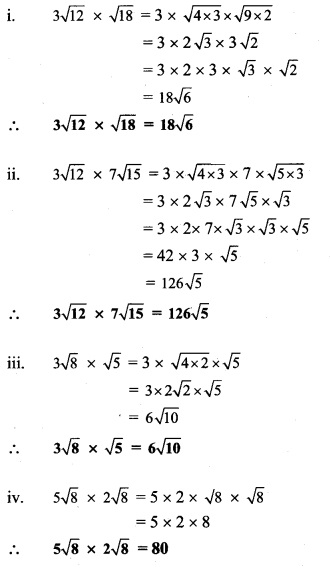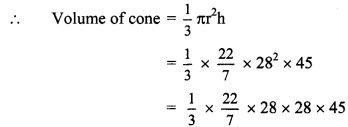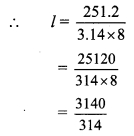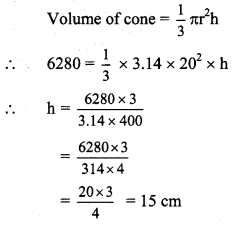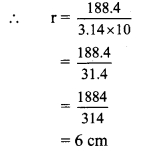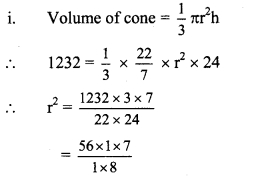Balbharti Maharashtra State Board Class 9 Maths Solutions covers the Problem Set 1 Algebra 9th Class Maths Part 1 Answers Solutions Chapter 1 Sets.

Problem Set 1 Algebra 9th Std Maths Part 1 Answers Chapter 1 Sets

Question 1.
Choose the correct alternative answer for each of the following questions.
i. M= {1, 3, 5}, N= {2, 4, 6}, then M ∩ N = ?
(A) {1, 2, 3, 4, 5, 6}
(B) {1, 3, 5}
(C) φ
(D) {2, 4, 6}
Answer:
(C) φ

ii. P = {x | x is an odd natural number, 1< x ≤ 5}. How to write this set in roster form?
(A) {1, 3, 5}
(B) {1, 2, 3, 4, 5}
(C) {1, 3}
(D) {3, 5}
Answer:
(D) {3, 5}

iii. P= {1, 2, ………. , 10}. What type of set Pis?
(A) Null set
(B) Infinite set
(C) Finite set
(D) None of these
Answer:
(C) Finite set

iv. M ∪ N = {1, 2, 3, 4, 5, 6} and M = {1, 2, 4}, then which of the following represent set N ?
(A) {1, 2, 3}
(B) {3, 4, 5, 6}
(C) {2, 5, 6}
(D) {4, 5, 6}
Answer:
(B) {3, 4, 5, 6}

v. If P ⊆ M, then which of the following set represent P ∩ (P ∪ M)?
(A) P
(B) M
(C) P ∪ M
(D) P’ ∩ M
Answer:
(A) P

vi. Which of the following sets are empty sets?
(A) Set of intersecting points of parallel lines.
(B) Set of even prime numbers.
(C) Month of an english calendar having less than 30 days.
(D) P = {x | x ∈ I , – 1 < x < 1}
Answer:
(A) Set of intersecting points of parallel lines.

Hints:
v. Here, P ⊆ M
∴ P ∪ M = M
∴ P ∩ (P ∪ M) = P ∩ M
= P … [∵ P ⊆M]

Question 2.
Find the correct option for the given question.
i. Which of the following collections is a set ?
(A) Colors of the rainbow
(B) Tall trees in the school campus.
(C) Rich people in the village
(D) Easy examples in the book
Answer:
(A) Colors of the rainbow

ii. Which of the following set represent N ∩W?
(A) {1, 2, 3,….}
(B) {0, 1, 2, 3,….}
(C) {0}
(D) { }
Answer:
(A) {1, 2, 3,….}

iii. P = {x | x is an odd natural number, 1< x < 5}. How to write this set in roster form?
(A) {1, 3, 5}
(B) {1, 2, 3, 4, 5}
(C) {1, 3}
(D) {3, 5}
Answer:
(B) {1, 2, 3, 4, 5}

iv. If T = {1, 2, 3, 4, 5} and M = {3,4, 7, 8}, then T ∪ M = ?
(A) {1, 2, 3, 4, 5,7}
(B) {1, 2, 3, 7, 8}
(C) {1, 2, 3, 4, 5, 7, 8}
(D) {3, 4}
Answer:
(C) {1, 2, 3, 4, 5, 7, 8}

Hints:
i. The elements of options B, C and D cannot be definitely and clearly decided.
ii. The common elements of N and W are 1 2, 3,….

Question 3.
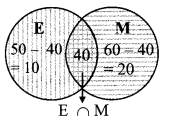
Out of 100 persons in a group, 72 persons speak English and 43 persons speak French. Each one out of 100 persons speak at least one language. Then how many speak only English? How many speak only French ? How many of them speak English and French both?
Solution:
i. Let U be the set of all the persons,
E be the set of persons who speak English and
F be the set of persons who speak French.
∴ n(E) = 72, n(F) = 43
Since, each one out of 100 persons speak at least one language
∴ n(U) = n(E ∪ F)= 100,

ii. n (E ∪ F) = n (E) + n (F) – n(E ∩ F)
100 = 72 + 43 – n (E ∩ F)
n (E ∩ F) = 72 + 43 – 100
∴ n(E ∩ F) = 15
Number of people who speak English and French = 15

iii. Number of people who speak only English = n(E) – n(E ∩ F)
= 72 – 15 = 57

iv. Number of
people who speak only French = n(F) – n(E ∩ F)
= 43 – 15 = 28

Alternate Method:
Let U be the set of all the persons,
E be the set of persons who speak English,
F be the set of persons who speak French and x people speak both the languages.

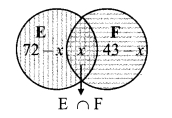
Since, each one out of 100 persons speak at least one language.
∴ n(U) = n(E ∪ F) = 100
∴ 72 – x + x + 43 – x = 100
∴ 115 – x= 100
∴ x = 115 – 100= 15.
Number of people who speak English and French = 15
Number of people who speak only English = 72 – x = 72 – 15 = 57
Number of people who speak only French = 43 – x = 43 – 15 = 28

Question 4.
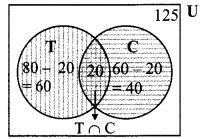
70 trees were planted by Parth and 90 trees were planted by Pradnya on the occasion of Tree Plantation Week. Out of these 25 trees were planted by both of them together. How many trees were planted by Parth or Pradnya?
Solution:
i. Let P be the trees planted by Parth and Q be the trees planted by Pradnya
∴ n(P) = 70 and n(Q) = 90
Total number of trees planted by Parth and Pradnya = n(P ∩ Q) = 25

ii. Number of trees planted by Parth or Pradnya = n(P ∪ Q)
= n(P) + n(Q) – n(P ∩ Q)
= 70 + 90 – 25 = 135
∴ A total of 135 trees were planted by Parth or Pradnya.

Alternate Method:
Let P be the trees planted by Parth and Q be the trees planted by Pradnya

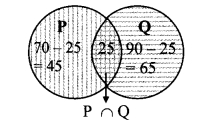
From Venn diagram
∴ Total trees planted by parth or pradnya = n(P ∪ Q)
= 45 + 25 + 65
= 135
A total of 135 trees were planted by Parth or Pradnya.

Question 5.
If n(A) = 20, n(B) = 28 and n(A ∪ B) = 36, then n(A ∩ B) = ?
Solution:
n(A ∪ B) = n(A) + n(B) – n(A ∩ B)
∴ 36 = 20 + 28 – n(A ∩ B)
∴ n(A ∩ B) = 20 + 28 – 36
∴ n(A ∩ B) = 12

Question 6.
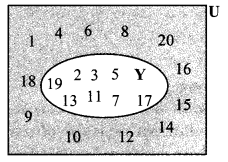
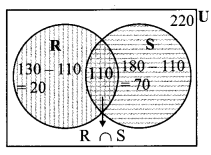
In a class, 8 students out of 28 have a dog as their pet animal at home, 6 students have a cat as their pet animal, 10 students have dog and cat both, then how many students do not have dog or cat as their pet animal at home?
Solution:
i. Let U be the set of all the students, then n(U) = 28
Let D be the set of students who have dog as pet and C be the set of students who have cat as pet.
10 students have dog and cat as their pet animal
n(D ∩ C) = 10

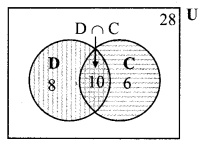
From venn diagram,

ii. Number of students who have cat or dog as pet
= n(D ∪ C)
= 8 + 10 + 6
= 24

iii. Number of students who do not have dog or cat as pet = n (U) – n(D ∪ C)
= 28 – 24
= 4

Question 7.
Represent the union of two sets by Venn diagram for each of the following.
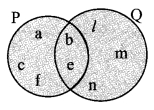
i. A = {3, 4, 5, 7},B = {1, 4, 8} l Marks
ii. P {a, b, c, e, f, Q = {l, m, n, e, b) I Markj
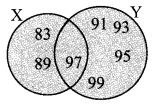
iii. X = {x x is a prime number between 80 and 100}
Y = { y | y is an odd number between 90 and 100}
Solution:
i. A = {3, 4, 5, 7}, B = {1, 4, 8}

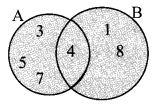
ii. P = {a, b, c, e, f}, Q = {l, m, n, e, b}

iii. X = {x | x is a prime number between 80 and 100}
∴ X = {83, 89, 97}
Y = {y | y is an odd number between 90 and 100}
∴ Y = {91, 93, 95, 97, 99}

Question 8.
Write the subset relations between the following sets.
X = set of all quadrilaterals.
Y = set of all rhombuses.
S = set of all squares.
T = set of all parallelograms.
V = set of all rectangles. [3 Marks]
Solution:
i. Rhombus, square, parallelogram and rectangle all are quadrilaterals.
∴ Y ⊆ X,S ⊆ X,T ⊆ X,V ⊆ X

ii. Every square is a rhombus, parallelogram and rectangle.
∴ S ⊆ Y, S ⊆ T, S ⊆ V

iii. Every rhombus and rectangle is a parallelogram.
∴ Y ⊆ T, V ⊆ T

Question 9.
If M is any set, then write M ∪Φ and M ∩ Φ.
Solution:
Let M = {2, 3, 4, 8} and Φ = { }
∴ M ∪ Φ = {2, 3, 4, 8}
∴ M ∪ Φ = M Also, M ∩ Φ = { }
∴ M ∩ Φ = i(i

Question 10.
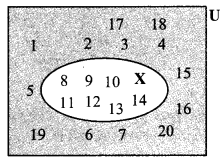
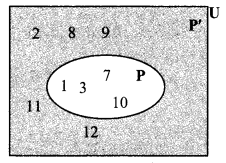
Observe the Venn diagram and write the given sets U, A, B, A ∪ B and A ∩ B.

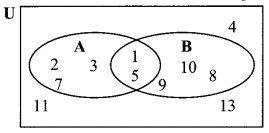
U = {1,2, 3,4, 5, 7, 8, 9, 10, 11, 13}
A = {1, 2, 3, 5,7}
B = {1, 5, 8, 9, 10}
A ∪ B = {1,2, 3, 5, 7, 8, 9, 10}
A ∩ B = {1, 5}

Question 11.
If n(A) = 7, n(B) = 13, n(A ∩ B) = 4, then n(A ∪ B) = ?
Solution:
n(A ∪ B) = n(A) + n(B) – n(A ∩ B)
= 7 + 13 – 4
n(A ∪ B) = 16

Question 1.
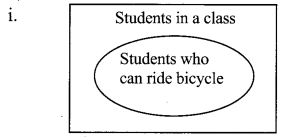
Set of students in a class and set of students in the same class who can swim, are shown by the Venn diagram.

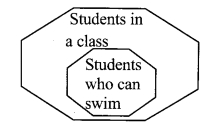
Observe the diagram and draw Venn diagrams for the following subsets.
i. a. Set of students in a class
b. Set of students who can ride bicycles in the same class

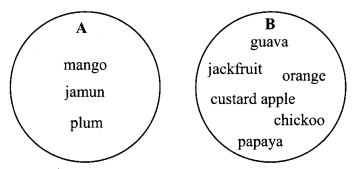
ii. A set of fruits is given as follows.
U = {guava, orange, mango, jackfruit, chickoo, jamun, custard apple, papaya, plum}
Show these subsets.
A = fruit with one seed
B = fruit with more than one seed. (Textbook pg. no. 8)
Solution:

ii. A = {mango, jamun, plum}
B = {guava, orange, jackfruit, chickoo, custard apple, papaya}

Question 2.
Every student should take 9 triangular sheets of paper and one plate. Numbers from 1 to 9 should, be written on each triangle. Everyone should keep some numbered triangles in the plate. Now the triangles in each plate form a subset of the set of numbers from 1 to 9.

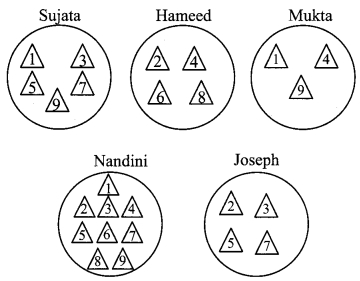
Look at the plates of Sujata, Hameed, Mukta, Nandini, Joseph with the numbered triangles. Guess the thinking behind selecting these numbers. Hence write the subsets in set builder form. (Textbook pg, no. 9)
Solution:
Sujata:
S = {x | x = 2n- 1, n ∈ N, x < 9}
Hameed:
f H = {x | x = 2n, n ∈ N, x < 9}
Mukta:
M = {x | x = n², n ∈ N, x ≤ 9}
Nandini:
N = {x | x ∈ N, x ≤ 9}
Joseph:
J = {x | x is a prime number between 1 and 9}

Question 3.
Collect the following information from 20 families nearby your house.
i. Number of families subscribing for Marathi Newspaper.
ii. Number of families subscribing for English Newspaper.
iii. Number of families subscribing for both English as well as Marathi Newspaper.
Show the collected information using Venn diagram. (Textbook pg.no. 18)
[Students should attempt the above activity on their own.]

Balbharti Maharashtra State Board Class 9 Maths Solutions covers the Practice Set 2.1 Algebra 9th Class Maths Part 1 Answers Solutions Chapter 2 Real Numbers.

Practice Set 2.1 Algebra 9th Std Maths Part 1 Answers Chapter 2 Real Numbers

Question 1.
Classify the decimal form of the given rational numbers into terminating and non-terminating recurring type.

Solution:
i. Denominator = 5 = 1 x 5
Since, 5 is the only prime factor denominator.
the decimal form of the rational number \(\frac { 13 }{ 5 }\) will be terminating type.

ii. Denominator = 11 = 1 x 11
Since, the denominator is other than prime factors 2 or 5.
∴ the decimal form of the rational number \(\frac { 2 }{ 11 }\) will be non-terminating recurring type.

iii. Denominator = 16
= 2 x 2 x 2 x 2
Since, 2 is the only prime factor in the denominator.
∴ the decimal form of the rational number \(\frac { 29 }{ 16 }\) will be terminating type.

iv. Denominator = 125
= 5 x 5 x 5
Since, 5 is the only prime factor in the denominator.
the decimal form of the rational number \(\frac { 17 }{ 125 }\) will be terminating type.

v. Denominator = 6
= 2 x 3
Since, the denominator is other than prime factors 2 or 5.
∴ the decimal form of the rational number \(\frac { 11 }{ 6 }\) will be non-terminating recurring type.

Question 2.
Write the following rational numbers in decimal form.





Solution:
i. \(\frac { -5 }{ 7 }\)

ii. \(\frac { 9 }{ 11 }\)

iii. √5

iv. \(\frac { 121 }{ 13 }\)

v. \(\frac { 29 }{ 8 }\)

Question 3.
Write the following rational numbers in \(\frac { p }{ q }\) form.

Solution:
i. Let x = \(0.\dot { 6 }\) …(i)
∴ x = 0.666…
Since, one number i.e. 6 is repeating after the decimal point.
Thus, multiplying both sides by 10,
10x = 6.666…
∴ 10 x 6.6 …(ii)
Subtracting (i) from (ii),
10x – x = 6.6 – 0.6
∴ 9x = 6

ii. Let x = \(0.\overline { 37 }\)
∴ x = 0.3737…
Since, two numbers i.e. 3 and 7 are repeating after the decimal point.
Thus, multiplying both sides by 100,
100x = 37.3737……
∴ 100x = \(37.\overline { 37 }\) ……(ii)
Subtracting (i) from (ii),
100x – x = \(37.\overline { 37 }\) – \(0.\overline { 37 }\)
∴ 99x = 37

iii. Letx = \(3.\overline { 17 }\) …(i)
∴ x = 3.1717…
Since, two numbers i.e. 1 and 7 are repeating after the decimal point.
Thus, multiplying both sides by 100,
100x = 317.1717…
∴ 100x= 317.17 …(ii)
Subtracting (i) from (ii),
100x – x = \(317.\overline { 17 }\) – \(3.\overline { 17 }\)
∴ 99x = 314

iv. Let x = \(15.\overline { 89 }\) …….. (i)
∴ x = 15.8989…
Since, two numbers i.e. 8 and 9 are repeating after the decimal point.
Thus, multiplying both sides by 100,
100x= 1589.8989…
∴ 100x = \(1589.\overline { 89 }\) …(ii)
Subtracting (i) from (ii),
100x – x = \(1589.\overline { 89 }\) – \(15.\overline { 89 }\)
∴ 99x = 1574

v. Let x = \(2.\overline { 514 }\)
∴ x = 2.514514…
Since, three numbers i.e. 5, 1 and 4 are repeating after the decimal point.
Thus, multiplying both sides by 1000,
1000x = 2514.514514…
1000x = \(2514.\overline { 514 }\) ….(ii)
Subtracting (i) from (ii),
1000x – x = \(2514.\overline { 514 }\) – \(2.\overline { 514 }\)
∴ 999x = 2512

Question 1.
How to convert 2.43 in \(\frac { p }{ q }\) form ? (Textbook pg. no. 20)
Solution:
Let x = 2.43
In 2.43, the number 4 on the right side of the decimal point is not recurring.
So, in order to get only recurring digits on the right side of the decimal point, we will multiply 2.43 by 10.
∴ 10x = 24.3 …(i)
∴ 10x = 24.333…
Here, digit 3 is the only recurring digit. Thus, by multiplying both sides by 10, 100x = 243.333…
∴ 100x= 243.3 …(ii)
Subtracting (i) from (ii),
100x – 10x = 243.3 – 24.3
∴ 90x = 219

Balbharti Maharashtra State Board Class 9 Maths Solutions covers the Practice Set 1.3 Algebra 9th Class Maths Part 1 Answers Solutions Chapter 1 Sets.

Practice Set 1.3 Algebra 9th Std Maths Part 1 Answers Chapter 1 Sets

Question 1.
If A = {a, b, c, d, e}, B = {c, d, e, f}, C = {b, d}, D = {a, e}, then which of the following statements are true and which are false?
i. C ⊆ 3
ii. A ⊆ D
iii. D ⊆ B
iv. D ⊆ A
V. B ⊆ A
vi. C ⊆ A
Ans:
i. C = {b, d}, B = {c, d, e ,f}
C ⊆ B
False
Since, all the elements of C are not present in B.

ii. A = {a, b, c, d, e}, D = {a, e}
A ⊆ D
False
Since, all the elements of A are not present in D.

iii. D = {a, e}, B = {c, d, e, f}
D ⊆ B
False
Since, all the elements of D are not present in B.

iv. D = {a, e}, A = {a, b, c, d, e}
D ⊆ A
True
Since, all the elements of D are present in A.

v. B = {c, d, e, f}, A = {a, b, c, d, e}
B ⊆ A
False
Since, all the elements of B are not present in A.

vi. C = {b, d}, A= {a, b, c, d, e}
C ⊆A
True
Since, all the elements of C are present in A.

Question 2.
Take the set of natural numbers from 1 to 20 as universal set and show set X and Y using Venn diagram. [2 Marks each]
i. X= {x |x ∈ N, and 7 < x < 15}
ii. Y = { y | y ∈ N, y is a prime number from 1 to 20}
Answer:
i. U = {1, 2, 3, 4, …….., 18, 19, 20}
x = {x | x ∈ N, and 7 < x < 15}
∴ x = {8, 9, 10, 11, 12, 13, 14}

ii. U = {1, 2, 3, 4, …… ,18, 19, 20}
Y = { y | y ∈ N, y is a prime number from 1 to 20}
∴ Y = {2, 3, 5, 7, 11, 13, 17, 19}

Question 3.
U = {1, 2, 3, 7, 8, 9, 10, 11, 12} P = {1, 3, 7,10}, then
i. show the sets U, P and P’ by Venn diagram.
ii. Verify (P’)’ = P
Solution:
i. Here, U = {1,2, 3, 7, 8,9, 10, 11, 12} P = {1, 3, 7, 10}
∴ P’ = {2, 8, 9, 11, 12}

II. Here, U = {1, 2, 3, 7, 8, 9, 10, 11, 12}
P = {1, 3, 7, 10} ….(i)
∴ P’= {2, 8, 9, 11, 12}
Also, (P’)’ = {1,3,7, 10} …(ii)
∴ (P’)’ = P … [From (i) and (ii)]

Question 4.
A = {1, 3, 2, 7}, then write any three subsets of A.
Solution:
Three subsets of A:
i. B = {3}
ii. C = {2, 1}
iii. D= {1, 2, 7}
[Note: The above problem has many solutions. Students may write solutions other than the ones given]

Question 5.
i. Write the subset relation between the sets.
P is the set of all residents in Pune.
M is the set of all residents in Madhya Pradesh.
I is the set of all residents in Indore.
B is the set of all residents in India.
H is the set of all residents in Maharashtra.

ii. Which set can be the universal set for above sets ?
Solution:
i.
a. The residents of Pune are residents of India.
∴ P ⊆ B
b. The residents of Pune are residents of Maharashtra.
∴ P ⊆ H
c. The residents of Madhya Pradesh are residents of India.
∴ M ⊆ B
d. The residents of Indore are residents of India.
∴ I ⊆ B
e. The residents of Indore are residents of Madhya Pradesh.
∴ I ⊆ M
f. The residents of Maharashtra are residents of India.
∴ H ⊆B

ii. The residents of Pune, Madhya Pradesh, Indore and Maharashtra are all residents of India.
∴ B can be the Universal set for the above sets.

Question 6.
Which set of numbers could be the universal set for the sets given below?
i. A = set of multiples of 5,
B = set of multiples of 7,
C = set of multiples of 12

ii. P = set of integers which are multiples of 4.
T = set of all even square numbers.
Answer:
i. A = set of multiples of 5
∴ A = {5, 10, 15, …}
B = set of multiples of 7
∴ B = {7, 14, 21,…}
C = set of multiples of 12
∴ C = {12, 24, 36, …}
Now, set of natural numbers, whole numbers, integers, rational numbers are as follows:
N = {1, 2, 3, …}, W = {0, 1, 2, 3, …}
I = {…,-3, -2, -1, 0, 1, 2, 3, …}
Q = { \(\frac { p }{ q }\) | p,q ∈ I,q ≠ 0}
Since, set A, B and C are the subsets of sets N, W , I and Q.
∴ For set A, B and C we can take any one of the set from N, W, I or Q as universal set.

ii. P = set of integers which are multiples of 4.
P = {4, 8, 12,…}
T = set of all even square numbers T = {2², 4², 6², …]
Since, set P and T are the subsets of sets N, W, I and Q.
∴ For set P and T we can take any one of the set from N, W, I or Q as universal set.

Question 7.
Let all the students of a class form a Universal set. Let set A be the students who secure 50% or more marks in Maths. Then write the complement of set A.
Answer:
Here, U = all the students of a class.
A = Students who secured 50% or more marks in Maths.
∴ A’= Students who secured less than 50% marks in Maths.

Question 1.
If A = {1, 3, 4, 7, 8}, then write all possible subsets of A.
i. e. P = {1, 3}, T = {4, 7, 8}, V = {1, 4, 8}, S = {1, 4, 7, 8}
In this way many subsets can be written. Write five more subsets of set A. (Textbook pg. no, 8)
Answer:
B = { },
E = {4},
C = {1, 4},
D = {3, 4, 7},
F = {3, 4, 7,8}

Question 2.
Some sets are given below.
A ={…,-4, -2, 0, 2, 4, 6,…}
B = {1, 2, 3,…}
C = {…,-12, -6, 0, 6, 12, 18, }
D = {…, -8, -4, 0, 4, 8,…}
I = {…,-3, -2, -1, 0, 1, 2, 3, 4, }
Discuss and decide which of the following statements are true.
a. A is a subset of sets B, C and D.
b. B is a subset of all the sets which are given above. (Textbook pg. no. 9)
Solution:
a. All elements of set A are not present in set B, C and D.
∴ A ⊆ B,
∴ A ⊆ C,
∴ A ⊆ D
∴ Statement (a) is false.

b. All elements of set B are not present in set A, C and D.
∴ B ⊆ A,
∴ B ⊆ C,
∴ B ⊆ D
∴ Statement (b) is false.

Question 3.
Suppose U = {1, 3, 9, 11, 13, 18, 19}, and B = {3, 9, 11, 13}. Find (B’)’ and draw the inference. (Textbook pg. no. 10)

Solution:
U = {1, 3, 9, 11, 13, 18, 19},
B= {3, 9, 11, 13} ….(i)
∴ B’= {1, 18, 19}
(B’)’= {3, 9, 11, 13} ….(ii)
∴ (B’)’ = B … [From (i) and (ii)]
∴ Complement of a complement is the given set itself.

Balbharti Maharashtra State Board Class 9 Maths Solutions covers the Practice Set 1.2 Algebra 9th Class Maths Part 1 Answers Solutions Chapter 1 Sets.

Practice Set 1.2 Algebra 9th Std Maths Part 1 Answers Chapter 1 Sets

Question 1.
Decide which of the following are equal sets and which are not ? Justify your answer.
A= {x | 3x – 1 = 2}
B = {x | x is a natural number but x is neither prime nor composite}
C = {x | x e N, x < 2}
Solution:
A= {x | 3x – 1 = 2}
Here, 3x – 1 = 2
∴ 3x = 3
∴ x = 1
∴ A = {1} …(i)

B = {x | x is a natural number but x is neither prime nor composite}
1 is the only number which is neither prime nor composite,
∴ x = 1
∴ B = {1} …(ii)

C = {x | x G N, x < 2}
1 is the only natural number less than 2.
∴ x = 1
∴ C = {1} …(iii)
∴ The element in sets A, B and C is identical. … [From (i), (ii) and (iii)]
∴ A, B and C are equal sets.

Question 2.
Decide whether set A and B are equal sets. Give reason for your answer.
A = Even prime numbers
B = {x | 7x – 1 = 13}
Solution:
A = Even prime numbers
Since 2 is the only even prime number,
∴ A = {2} …(i)
B= {x | 7x – 1 = 13}
Here, 7x – 1 = 13
∴ 7x = 14
∴ x = 2
∴ B = {2} …(ii)
∴ The element in set A and B is identical. … [From (i) and (ii)]
∴ A and B are equal sets.

Question 3.
Which of the following are empty sets? Why?
i. A = {a | a is a natural number smaller than zero}
ii. B = {x | x² = 0}
iii. C = {x | 5x – 2 = 0, x ∈N}
Solution:
i. A = {a| a is a natural number smaller than zero}
Natural numbers begin from 1.
∴ A = { }
∴ A is an empty set.

ii. B = {x | x² = 0}
Here, x² = 0
∴ x = 0 … [Taking square root on both sides]
∴ B = {0}
∴B is not an empty set.

iii. C = {x | 5x – 2 = 0, x ∈ N}
Here, 5x – 2 = 0
∴ 5x = 2
∴ x = \(\frac { 2 }{ 5 }\)
Given, x ∈ N
But, x = \(\frac { 2 }{ 5 }\) is not a natural number.
∴ C = { }
∴ C is an empty set.

Question 4.
Write with reasons, which of the following sets are finite or infinite.
i. A = {x | x<10, xisa natural number}
ii. B = {y | y < -1, y is an integer}
iii. C = Set of students of class 9 from your school.
iv. Set of people from your village.
v. Set of apparatus in laboratory
vi. Set of whole numbers
vii. Set of rational number
Solution:
i. A={x| x < 10, x is a natural number}
∴ A = {1,2, 3,4, 5,6, 7, 8, 9}
The number of elements in A are limited and can be counted.
∴A is a finite set.

ii. B = (y | y < -1, y is an integer}
∴ B = { …,-4, -3, -2}
The number of elements in B are unlimited and uncountable.
∴ B is an infinite set.

iii. C = Set of students of class 9 from your school.
The number of students in a class is limited and can be counted.
∴ C is a finite set.

iv. Set of people from your village.
The number of people in a village is limited and can be counted.
∴ Given set is a finite set.

v. Set of apparatus in laboratory
The number of apparatus in the laboratory are limited and can be counted.
∴ Given set is a finite set.

vi. Set of whole numbers
The number of elements in the set of whole numbers are unlimited and uncountable.
∴ Given set is an infinite set.

vii. Set of rational number
The number of elements in the set of rational numbers are unlimited and uncountable.
∴ Given set is an infinite set.

Question 1.
If A = {1, 2, 3} and B = {1, 2, 3, 4}, then A ≠ B verify it. (Textbook pg. no. 6)
Answer:
Here, 4 ∈ B but 4 ∉ A
∴ A and B are not equal sets,
i.e. A ≠ B

Question 2.
A = {x | x is prime number and 10 < x < 20} and B = {11,13,17,19}. Here A = B. Verify. (Textbook pg. no. 6)
Answer:
A = {x | x is prime number and 10 < x < 20}
∴ A = {11, 13, 17, 19}
B = {11, 13, 17, 19}
∴ All the elements in set A and B are identical.
∴ A and B are equal sets, i.e. A = B

Balbharti Maharashtra State Board Class 9 Maths Solutions covers the Practice Set 7.1 Geometry 9th Class Maths Part 2 Answers Solutions Chapter 7 Co-ordinate Geometry.

Practice Set 7.1 Geometry 9th Std Maths Part 2 Answers Chapter 7 Co-ordinate Geometry

Question 1.
State in which quadrant or on which axis do the following points lie.
i. A(-3, 2)
ii. B(-5, -2)
iii. K(3.5, 1.5)
iv. D(2, 10)
V. E(37, 35)
vi. F(15, -18)
vii. G(3, -7)
viii. H(0, -5)
ix. M(12, 0)
x. N(0, 9)
xi. P(0, 2.5)
xii. Q(-7, -3)
Solution:

Question 2.
In which quadrant are the following points?
i. whose both co-ordinates are positive.
ii. whose both co-ordinates are negative.
iii. whose x co-ordinate is positive and the y co-ordinate is negative.
iv. whose x co-ordinate is negative and y co-ordinate is positive.
Solution:
i. Quadrant I
ii. Quadrant III
iii. Quadrant IV
iv. Quadrant II

Question 3.
Draw the co-ordinate system on a plane and plot the following points.
L(-2, 4), M(5, 6), N(-3, -4), P(2, -3), Q(6, -5), S(7, 0), T(0, -5)
Solution:

Maharashtra Board Class 9 Maths Chapter 7 Co-ordinate Geometry Practice Set 7.1 Intext Questions and Activities

Question 1.
Plot the points R(-3,-4), S(3,-l) on the same co-ordinate system. (Textbook pg. no. 93)
Steps for plotting the points:
i. Draw X-axis and Y-axis on the plane. Show the origin.
ii. Draw a line parallel to Y-axis at a distance of 3 units in the -ve direction of X-axis.
iii. Draw another line parallel to X-axis at a distance of 4 units in the -ve direction of Y-axis.
iv. Intersection of these lines is the point R (-3, -4).
v. The point S can be plotted in the same manner.

Balbharti Maharashtra State Board Class 9 Maths Solutions covers the Practice Set 1.4 Algebra 9th Class Maths Part 1 Answers Solutions Chapter 1 Sets.

Practice Set 1.4 Algebra 9th Std Maths Part 1 Answers Chapter 1 Sets

Question 1.
If n(A) = 15, n(A ∪ B) = 29, n(A ∩ B) = 7, then n(B) = ?
Solution:
Here, n(A) = 15, n(A ∪ B) = 29, n(A ∩ B) = 7
n(A ∪ B) = n(A) + n(B) – n(A ∩ B)
∴ 29 = 15 + n(B) – 7
∴ 29 – 15 + 7 = n(B)
∴ n(B) = 21

Question 2.
In a hostel there are 125 students, out of which 80 drink tea, 60 drink coffee and 20 drink tea and coffee both. Find the number of students who do not drink tea or coffee.
Solution:
i. Let U be the set of students in the hostel, T be the set of students who drink tea and C be the set of students who drink coffee.
n(U) = 125, n(T) = 80, n(C) = 60,
number of students who drink Tea and Coffee = n(T ∩ C) = 20

ii. n(T ∪ C) = n(T) + n(C) – n(T ∩ C)
= 80 + 60 – 20
∴ n(T ∪ C) = 120
∴ 120 students drink tea or coffee
Also, there are 125 students in the hostel.

iii. Number of students who do not drink tea or coffee = n(U) – n(T ∪ C)
= 125 – 120
= 5
∴ 5 students do not drink tea or coffee.

Alternate Method:
Let U be the set of students in the hostel, T be the set of students who drink tea and C be the set of students who drink coffee.

From Venn diagram,
Student who drinks tea or coffee = n(T ∪ C) = 60 + 20 + 40 = 120
∴ The number of students who do not drink tea or coffee = n(U) – n(T ∪ C)
= 125 – 120 = 5
∴ 5 students do not drink tea or coffee.

Question 3.
In a competitive exam 50 students passed in English, 60 students passed in Mathematics and 40 students passed in both the subjects. None of them failed in both the subjects. Find the number of students who passed at least in one of the subjects ?
Solution:
Let U be the set of students who appeared for the exam,
E be the set of students who passed in English and
M be the set of students who passed in Maths.
∴ n(E) = 50, n(M) = 60,
40 students passed in both the subjects
∴ n(M ∩ E) = 40
Since, none of the students failed in both subjects
∴ Total students = n(E ∪M)
= n(E) + n(M) – n(E ∩ M)
= 50 + 60 – 40
= 70
∴ The number of students who passed at least in one of the subjects is 70.

Alternate Method:
Let U be the set of students who appeared for the exam,
E be the set of students who passed in English and M be the set of students who passed in Maths.

Since, none of the students failed in both subjects
∴ Total student = n(E ∪M)
= 10 + 40 + 20
= 70
∴ The number of students who passed at least in one of the subjects is 70.

Question 4.
A survey was conducted to know the hobby of 220 students of class IX. Out of which 130 students informed about their hobby as ’rock climbing and 180 students informed about their hobby as sky watching. There are 110 students who follow both the hobbies. Then how many students do not have any of the two hobbies? How many of them follow the hobby of rock climbing only? How many students follow the hobby of sky watching only?
Solution:
i. Let U be the set of students of class IX,
R be the set of students who follow the hobby of rock climbing and
S be the set of students who follow the hobby of sky watching.
∴ n (U) = 220, n (R) = 130, n (S) = 180,
110 students follow both the hobbies
∴ n (R ∩ S) = 110

ii. n(R ∪ S)=n (R) + n (S) – n (R ∩ S)
= 130 + 180 – 110
∴n (R ∪ S) = 200
∴ 200 students follow the hobby of rock climbing or sky watching.

iii. Total number of students = 220.
Number of students who do not follow the hobby of rock climbing or sky watching
= n (U) – n (R ∪ S)
= 220 – 200
= 20

iv. Number of students who follow the hobby of rock climbing only
= n (R) – n(R ∩ S)
= 130 – 110
= 20

v. Number of students who follow the hobby of sky watching only
= n (S) – n (R ∩ S)
= 180 – 110
= 70

Alternate Method:
Let U be the set of students of class IX,
R be the set of students who follow the hobby of rock climbing and
S be the set of students who follow the hobby of sky watching.

From the Venn diagram
i. Students who follow the hobby of rock climbing or sky watching
= n(R ∪ S)
= 20 + 110 + 70
= 200

ii. Number of students who do not follow the hobby of rock climbing or sky watching
= n (U) – n(R ∪S)
= 220 – 200
= 20

iii. Number of students who follow the hobby of rock climbing only
= n (R) – n(R ∩S)
= 130 – 110
= 20

iv. Number of students who follow the hobby of sky watching only
= n (S) – n (R ∩ S)
= 180 – 110
= 70

Question 5.
Observe the given Venn diagram and write the following sets.

i. A
ii. B
iii. A ∪ B
iv. U
v. A’
vi. B’
vii. (A ∪B )’
Ans:
i. A = {x, y, z, m, n}
ii. B = {p, q, r, m, n}
iii. A ∪ B = {x, y, z, m, n, p, q, r }
iv. U = {x, y, z, m, n, p, q, r, s, t}
v. A’ = {p, q, r, s, t}
vi. B’ = {x, y, z, s, t}
vii. (A ∪ B )’ = {s, t}

Question 1.
Take different examples of sets and verify the above mentioned properties. (Textbook pg.no. 12)
Solution:
i. Let A = {3, 5}, B= {3, 5, 8, 9, 10}
A ∩ B = B ∩ A = {3, 5}

ii. Let A = {3, 5}, B = {3, 5, 8, 9, 10}
Since, all elements of set A are present in set B.
∴ A ⊆ B
Also, A ∩ B = {3, 5} = A
∴ If A ⊆ B, then A ∩B = A.

iii. Let A = {2, 3, 8, 10}, B = {3,8}
A ∩ B = {3, 8} = B
Also, all the elements of set B are present in set A
∴ B ⊆ A
∴ If A ∩ B = B, then B ⊆ A.

iv. Let A = {2, 3, 8, 10}, B = {3, 8}, A ∩B = {3, 8}
Since, all the elements of set A n B are present in set A and B
A ∩ B ⊆ A and A ∩B ⊆B

v. Let U= {3, 4, 6, 8}, A = {6, 4}
∴ A’ = {3, 8}
∴ A ∩ A’= { } = φ

vi. A ∩ φ = { } = φ

vii. Let A = {6, 4}
∴ A ∩ A = {6, 4}
∴ A ∩ A = A

Question 2.
Observe the set A, B, C given by Venn diagrams and write which of these are disjoint sets. (Textbook pg. no. 12)

Solution:
Here, A = {1, 2, 3, 4, 5, 6, 7}
B = {3, 6, 8, 9, 10, 11, 12}
C = {10, 11, 12}
Now, A ∩ C = φ
∴ A and C are disjoint sets.

Question 3.
Let the set of English alphabets be the Universal set. The letters of the word ‘LAUGH’ is one set and the letter of the word ‘CRY’ is another set. Can we say that these are two disjoint sets? Observe that intersection of these two sets is empty. (Textbook pg. no. 13)

Solution:
Let A = {L, A, U, G, H}
B = {C, R, Y}
Now, A ∩ B = φ
∴ A and B are disjoint sets.

Question 4.
Fill in the blanks with elements of that set.
U = {1, 3, 5, 8, 9, 10, 11, 12, 13, 15}
A = {1,11, 13}
B = {8,5, 10, 11, 15}
A’ = { }
B’ = { }
A ∩ B = { }
A’ ∩ B’ = { }
A ∪ B = { }
A’ ∪ B’= { }
(A ∩ B)’ = { }
(A ∪ B)’ = { }
Verify: (A ∩ B)’ = A’ u B’, (A u B)’ = A’ ∩ B’ (Textbook pg. no, 18)
Solution:
U = {1, 3, 5, 8, 9, 10, 11, 12, 13, 15}
A = {1, 11, 13}
B = {8, 5, 10, 11, 15}
A’ = {3, 5, 8, 9, 10, 12, 15}
B’ = {1, 3, 9, 12, 13}
A∩ B= {11}
A’ ∩ B’= {3, 9, 12} …(i)
A ∪ B = {1, 5, 8, 10, 11, 13, 15}
A’ ∪ B’ = { 1, 3, 5, 8, 9, 10, 12, 13, 15} …(ii)
(A ∩ B)’= { 1, 3, 5, 8, 9, 10, 12, 13,15} …(iii)
(A ∪ B)’ = {3, 9, 12} ,..(iv)
(A ∩ B)’ = A’ ∪ B’ … [From (ii) and (iii)]
(A ∪ B)’ = A’ ∩ B’ … [From (i) and (iv)]

Question 5.
A = {1,2,3, 5, 7,9,11,13}
B = {1,2,4, 6, 8,12,13}
Verify the above rule for the given set A and set B. (Textbook pg. no. 14)
Solution:
A = {1, 2, 3, 5, 7, 9, 11, 13}
B = {1, 2, 4, 6, 8, 12, 13}
A ∪ B = {1, 2, 3, 4, 5, 6, 7, 8, 9, 11, 12, 13}
A ∩ B= {1, 2, 13}
n(A) = 8, n(B) = 7,
n(A ∪ B) = 12, n(A ∩ B) = 3
n(A ∩ B) = 12 …(i)
n(A) + n(B) – n(A ∩ B) = 8 + 7 – 3 = 12 …(ii)
∴ n(A ∪ B) = n(A) + n(B) – n(A ∩ B) … [From (i) and (ii)]

Question 6.
Verify the above rule for the given Venn diagram. (Textbook pg. no. 14)

Solution:
n(A) = 5 , n(B) = 6
n(A ∪ B) = 9 , n(A ∩ B) = 2
Now, n(A ∪ B) = 9 …(i)
n(A) + n(B) – n(A ∩ B) = 5 + 6 – 2 = 9 …(ii)
∴ n(A ∪ B) = n(A) + n(B) – n(A ∩ B). …[From (i) and (ii)]

Balbharti Maharashtra State Board Class 9 Maths Solutions covers the Practice Set 1.1 Algebra 9th Class Maths Part 1 Answers Solutions Chapter 1 Sets.

Practice Set 1.1 Algebra 9th Std Maths Part 1 Answers Chapter 1 Sets

Question 1.
Write the following sets in roster form.
i. Set of even natural numbers
ii. Set of even prime numbers from 1 to 50
iii. Set of negative integers
iv. Seven basic sounds of a sargam (sur)
Answer:
i. A = { 2, 4, 6, 8,….}
ii. 2 is the only even prime number
∴ B = { 2 }
iii. C = {-1, -2, -3,….}
iv. D = {sa, re, ga, ma, pa, dha, ni}

Question 2.
Write the following symbolic statements in words.
i. \(\frac { 4 }{ 3 }\) ∈ Q
ii. -2 ∉ N
iii. P = {p | p is an odd number}
Answer:
i. \(\frac { 4 }{ 3 }\) is an element of set Q.
ii. -2 is not an element of set N.
iii. Set P is a set of all p’s such that p is an odd number.

Question 3.
Write any two sets by listing method and by rule method.
Answer:
i. A is a set of even natural numbers less than 10.
Listing method: A = {2, 4, 6, 8}
Rule method: A = {x | x = 2n, n e N, n < 5}

ii. B is a set of letters of the word ‘SCIENCE’. Listing method : B = {S, C, I, E, N}
Rule method: B = {x \ x is a letter of the word ‘SCIENCE’}

Question 4.
Write the following sets using listing method.
i. All months in the Indian solar year.
ii. Letters in the word ‘COMPLEMENT’.
iii. Set of human sensory organs.
iv. Set of prime numbers from 1 to 20.
v. Names of continents of the world.
Answer:
i. A = {Chaitra, Vaishakh, Jyestha, Aashadha, Shravana, Bhadrapada, Ashwina, Kartika, Margashirsha, Paush, Magha, Falguna}
ii. X = {C, O, M, P, L, E, N, T}
iii. Y = {Nose, Ears, Eyes, Tongue, Skin}
iv. Z = {2, 3, 5, 7, 11, 13, 17, 19}
v. E = {Asia, Africa, Europe, Australia, Antarctica, South America, North America}

Question 5.
Write the following sets using rule method.
i. A = {1, 4, 9, 16, 25, 36, 49, 64, 81, 100}
ii. B= {6, 12, 18,24, 30,36,42,48}
iii. C = {S, M, I, L, E}
iv. D = {Sunday, Monday, Tuesday, Wednesday, Thursday, Friday, Saturday}
v. X = {a, e, t}
Answer:
i. A = {x | v = n², n e N, n < 10}
ii. B = {x j x = 6n, n e N, n < 9}
iii. C = {y j y is a letter of the word ‘SMILE’} [Other possible words: ‘SLIME’, ‘MILES’, ‘MISSILE’ etc.]
iv. D = {z | z is a day of the week}
v. X = {y | y is a letter of the word ‘eat’}
[Other possible words: ‘tea’ or ‘ate’]

Question 1.
Fill in the blanks given in the following table. (Textbook pg. no. 3)
Answer:

Balbharti Maharashtra State Board Class 9 Maths Solutions covers the Practice Set 9.2 Geometry 9th Class Maths Part 2 Answers Solutions Chapter 9 Surface Area and Volume.

Practice Set 9.2 Geometry 9th Std Maths Part 2 Answers Chapter 9 Surface Area and Volume

Question 1.
Perpendicular height of a cone is 12 cm and its slant height is 13 cm. Find the radius of the base of the cone.
Given: Height (h) = 12 cm, length (l) = 13 cm
To find: Radius of the base of the cone (r)
Solution:
l² = r² + h²
∴ 13² = r² + 12²
∴ 169 = r² + 144
∴169 – 144 = r²
∴ r² = 25
∴ r = √25 … [Taking square root on both sides]
= 5 cm
∴ The radius of base of the cone is 5 cm.

Question 2.
Find the volume of a cone, if its total surface area is 7128 sq.cm and radius of base is 28 cm. ( π = \(\frac { 22 }{ 7 }\))
Given: Radius (r) = 28 cm,
Total surface area of cone = 7128 sq.cm
To find: Volume of the cone
Solution:
i. Total surface area of cone = πr (l + r)
∴ 7128= y x 28 x (l + 28)
∴ 7128 = 22 x 4 x(l +28)
∴ l + 28 = \(\frac { 7128 }{ 22\times 4 }\)
∴ l + 28 = 81
∴ l = 81 – 28
∴ l = 53cm

ii. Now, l² = r² + h²
∴ 53² = 28²+ h²
∴ 2809 = 784 + h²
∴ 2809 – 784 = h²
∴ h² = 2025
∴ h = \(\sqrt { 2025 }\) …… [Taking square root on both sides]
= 45 cm

= 22 x 4 x 28 x 15
= 36960 cubic.cm
∴ The volume of the cone is 36960 cubic.cm.

Question 3.
Curved surface area of a cone is 251.2 cm² and radius of its base is 8 cm. Find its slant height and perpendicular height, (π = 3.14)
Given: Radius (r) = 8 cm, curved surface area
of cone = 251.2 cm²
To find: Slant height (l) and the perpendicular height (h) of the cone
Solution:
i. Curved surface area of cone = πrl
∴ 251.2 = 3.14 x 8 x l

∴ l= 10 cm

ii. Now, l² = r² + h²
∴ 10² = 8² + h²
∴ 100 = 64 + h²
∴ 100 – 64 = h²
∴ h² = 36
∴ h = √36 … [Taking square root on both sides]
= 6 cm
∴ The slant height and the perpendicular height of the cone are 10 cm and 6 cm respectively.

Question 4.
What will be the cost of making a closed cone of tin sheet having radius of base 6 m and slant height 8 m if the rate of making is ₹ 10 per sq.m?
Given: Radius (r) = 6 m, length (l) = 8 m
To find: Total cost of making the cone
Solution:
i. To find the total cost of making the cone of tin sheet, first we need to find the total surface area of the cone.
Total surface area of the cone = πr (l + r)
= \(\frac { 22 }{ 7 }\) x 6 x (8 + 6)
= \(\frac { 22 }{ 7 }\) x 6 x 14
= 22 x 6 x 2 = 264 sq.m

ii. Rate of making the cone = ₹ 10 per sq.m
∴ Total cost = Total surface area x Rate of making the cone
= 264 x 10
= ₹ 2640
∴ A The total cost of making the cone of tin sheet is ₹ 2640.

Question 5.
Volume of a cone is 6280 cubic cm and base radius of the cone is 20 cm. Find its perpendicular height, (π = 3.14)
Given: Radius (r) = 20 cm,
Volume of cone = 6280 cubic cm
To find: Perpendicular height (h) of the cone
Solution:

∴ The perpendicular height of the cone is 15 cm.

Question 6.
Surface area of a cone is 188.4 sq.cm and its slant height is 10 cm. Find its perpendicular height (π = 3.14).
Given: Length (l) =10 cm, curved surface area of the cone = 188.4 sq.cm
To find: Perpendicular height (h) of the cone
Solution:
i. Curved surface area of the cone = πrl
∴ 188.4 = 3.14 x r x 10

ii. Now, l² = r² + h²
∴ 10² = 6² + h²
∴ 100 = 36 + h²
∴ 100 – 36 = h²
∴ h² = 64
∴ h = \(\sqrt { 64 }\) … [Taking square root on both sides]
= 8 cm
∴ The perpendicular height of the cone is 8 cm.

Question 7.
Volume of a cone is 1232 cm³ and its height is 24 cm. Find the surface area of the cone. (π = \(\frac { 22 }{ 7 }\))
Given: Height (h) = 24 cm,
Volume of cone = 1232 cm³
To find: Surface area of the cone
Solution:

∴ r² = 49
∴ r = \(\sqrt { 49 }\) … [Taking square root on both sides]
= 7 cm

ii. Now, l² = r² + h²
∴ l² = 7² + 24²
= 49 + 576 = 625
∴ l = \(\sqrt { 625 }\) … [Taking square root on both sides]
= 25

iii. Curved surface area of cone = πrl
= \(\frac { 22 }{ 7 }\) x 7 x 25
= 22 x 25
= 550 sq.cm
∴The surface area of the cone is 550 sq.cm.

Question 8.
The curved surface area of a cone is 2200 sq.cm and its slant height is 50 cm. Find the total surface area of cone. (π = \(\frac { 22 }{ 7 }\))
Given: Length (l) = 50 cm, curved surface area of cone = 2200 sq.cm
To find: Total surface area of the cone
Solution:
i. Curved surface area of cone = πrl

ii. Total surface area of cone = πr (l + r)
= \(\frac { 22 }{ 7 }\) x 14 x (50 + 14)
= \(\frac { 22 }{ 7 }\) x 14 x 64
= 22 x 2 x 64
= 2816 sq.cm
∴ The total surface area of the cone is 2816 sq.cm.

Question 9.
There are 25 persons in a tent which is conical in shape. Every person needs an area of 4 sq.m, of the ground inside the tent. If height of the tent is 18 m, find the volume of the tent.
Given: For the tent,
height (h) = 18m,
number of people in the tent = 25,
area required for each person = 4 sq.m
To find: Volume of the tent
Solution:
i. Every person needs an area of 4 sq.m, of the ground inside the tent.
Surface area of the base of the tent = number of people in the tent × area required for each person
= 25 × 4
= 100 sq.m

ii. Surface area of the base of the tent = πr²
∴ 100 = πr²
∴ πr² = 100

iii. Volume of the tent= \(\frac { 1 }{ 3 }\) πr²h
= \(\frac { 1 }{ 3 }\) x 100 x 18 …….[∵ πr² = 100]
= 100 x 6
= 600 cubic metre
∴ The volume of the tent is 600 cubic metre.

Question 10.
In a field, dry fodder for the cattle is heaped in a conical shape. The height of the cone is 2.1 m and diameter of base is 7.2 m. Find the volume of the heap of the fodder. If it is to be covered by polythene in rainy se&son then how much minimum polythene
sheet is needed? (π = \(\frac { 22 }{ 7 }\) and \(\sqrt { 17.37 }\) = 4.17 ]
Given: Height of the heap (h) = 2.1 m.
diameter of the base (d) = 7.2 m
∴Radius of the base (r) = \(\frac { d }{ 2 }\) = \(\frac { 7.2 }{ 2 }\) = 3.6 m
To find: Volume of the heap of the fodder and polythene sheet required
Solution:
i. Volume of the heap of fodder = \(\frac { 1 }{ 3 }\)πr²h
= \(\frac { 1 }{ 3 }\) x \(\frac { 22 }{ 7 }\) x (3.6)² x 2.1
= \(\frac { 1 }{ 3 }\) x \(\frac { 22 }{ 7 }\) x 3.6 x 3.6 x 2.1
= 1 x 22 x 1.2 x 3.6 x 0.3
= 28.51 cubic metre

ii. Now, l² = r² + h²
= (3.6)² + (2.1)²
= 12.96 + 4.41
∴ l² =17.37
∴ l² = \(\sqrt { 17.37 }\) .. .[Taking square root on both sides]
= 4.17 m

iii. Area of the polythene sheet needed to cover the heap of the fodder = Curved surface area of the conical heap
= πrl
= \(\frac { 22 }{ 7 }\) x 3.6 x 4.17
= 47.18 sq.m
∴ The volume of the heap of the fodder is 28.51 cubic metre and a polythene sheet of 47.18 sq.m will be required to cover it.

Maharashtra Board Class 9 Maths Solutions

Balbharti Maharashtra State Board Class 9 Maths Solutions covers the Practice Set 9 Geometry 9th Class Maths Part 2 Answers Solutions Chapter 9 Surface Area and Volume.

Practice Set 9 Geometry 9th Std Maths Part 2 Answers Chapter 9 Surface Area and Volume

Question 1.
If diameter of a road roller is 0.9 m and its length is 1.4 m, how much area of a field will be pressed in its 500 rotations? ( π = \(\frac { 22 }{ 7 }\))
Given: For road roller,
diameter (d) = 0.9 m, length (h) = 1.4 m
To find: Area of a field pressed in 500 rotations
Solution:
i. Since, area of field pressed in 1 rotation of road roller = curved surface area of road roller
∴ Curved surface area of the road roller = 2πrh
= πdh ,..[∵ d = 2r]
= \(\frac { 22 }{ 7 }\) x 0.9 x 1.4 7
= 22 x 0.9 x 0.2
= 3.96 sq.m.

ii. Area of land pressed in 1 rotation = 3.96 sq.m.
∴Area of land pressed in 500 rotations = 500 x 3.96
= 1980 sq.m.
∴ 1980 sq.m, land will be pressed in 500 rotations of the road roller.

Question 2.
To make an open fish tank, a glass sheet of 2 mm gauge is used. The outer length, breadth and height of the tank are 60.4 cm, 40.4 cm and 40.2 cm respectively. How much maximum volume of water will be contained in it ?
Given: Thickness of the glass = 2 mm,
outer length of the tank = 60.4 cm,
outer breadth of the tank = 40.4 cm,
outer height of the tank = 40.2 cm
To find: Volume of water fish tank contains
Solution:

i. Thickness oldie glass = 2 mm.
= \(\frac { 2 }{ 10 }\) cm
= 0.2 cm
Outerlengthofthetank = 60.4 cm
∴ Inner length oldie tank (l) = Outer length – thickness oldie glass on both sides
= 60.4 – 0.2 – 0.2
= 60cm
Outer breadth oldie tank = 40.4 cm
∴ Inner breadth of the tank (b) = 40.4 – 0.2 – 0.2
= 40 cm
Outer height of the tank = 40.2 cm
∴Inner height of the tank (h) = 40.2 – 0.2
= 40 cm

ii. Maximum volume of water that can be contained in the tank = volume of the tank
= l x b x h
= 60 x 40 x 40
= 96000 cubic cm.
∴ The fishtank can contain maximum of 96000 cubic cm. water in it.

Question 3.
If the ratio of radius of base and height of a cone is 5 : 12 and its volume is 314 cubic metre. Find its perpendicular height and slant height (π = 3.14).
Given: Ratio of radius of base and height of a cone = 5 : 12,
Volume = 314 cubic metre
To find: Perpendicular height (h) and slant height (l)
Solution:
i. The ratio of radius and height of cone is 5 : 12
Let the common multiple be x.
∴ Radius of base (r) = 5x
Perpendicular height (h) = 12x

∴ x³ = 1
∴ x = 1 … [Taking cube root on both sides]
∴ r = 5x = 5(1) = 5m
h = 12x = 12(1) = 12 m

ii. Now, l² = r² + h²
= 5² + 12²
= 25 + 144
∴l² = 169
∴ l = \(\sqrt { 169 }\) … [Taking square root on both sides]
= 13 m
The perpendicular height and slant height of the cone are 12 m and 13 m respectively.

Question 4.
Find the radius of a sphere if its volume is 904.32 cubic cm. (π = 3.14)
Given: Volume of sphere = 904.32 cubic cm.
To find: Radius of a sphere
Solution:
Volume of sphere = \(\frac { 4 }{ 3 }\) πr³
∴ 904.32 = \(\frac { 4 }{ 3 }\) x 3.14 x r³

= 216
∴ r = \(\sqrt [ 3 ]{ 216 }\) … [Taking cube root on both sides]
= 6 cm
∴ The radius of the sphere is 6 cm.

Question 5.
Total surface area of a cube is 864 sq.cm. Find its volume.
Given: Total surface area of cube = 864 sq. cm
To find: Volume of cube
Solution:
i. Total surface area of cube = 6l²
∴ 864 = 6l²
∴ l²= \(\sqrt [ 864 ]{ 6 }\)
∴ l² = 144
∴ l = \(\sqrt { 144 }\) … [Taking square root on both sides]
= 12 cm

ii. Volume of cube = l²
= 12³
= 1728 cubic cm.
∴ The volume of cube is 1728 cubic cm.

Question 6.
Find the volume of a sphere, if its surface area is 154 sq.cm.
Given: Surface area of sphere = 154 sq. cm.
To find: Volume of sphere
Solution:
i. Surface area of sphere = 4πr²


∴ The volume of sphere is 179.67 cubic cm.

Question 7.
Total surface area of a cone is 616 sq.cm. If the slant ‘height of the cone Is three times the radius of its base, find its slant height.
Given: Total surface area of a cone = 616 sq.cm., slant height of the cone is three times the radius of its base
To find: Slant height (l)
Solution:
i. Let the radius of base be r cm.
∴ Slant height (l) = 3r cm
Total surface area of cone = πr (l + r)
∴ 616 = πr(l + r)
∴ 616 = \(\sqrt [ 22 ]{ 7 }\) x r x (3r + r)
∴ 616 = \(\sqrt [ 22 ]{ 7 }\) x 4r²

∴ r² = 49
∴ r = \(\sqrt { 49 }\) … [Taking square root on both sides]
= 7

ii. Slant height (l) = 3r = 3 x 7 = 21 cm
∴ The slant height of the cone is 21 cm.

Question 8.
The inner diameter of a well is 4.20 metre and its depth is 10 metre. Find the inner surface area of the well. Find the cost of plastering it from inside at the rate ₹ 52 per sq.m.
Given: Inner diameter (d) = 4.2 m,
To find: depth (h) = 10 m,
rate of plastering = ₹ 52 per sq.m.
Inner surface area and total cost of plastering
Solution:
i. Inner curved surface area of the well = 2πrh
= πdh …[∵ d = 2r]
= \(\sqrt [ 22 ]{ 7 }\) x 4.2 x 10
= \(\sqrt [ 22 ]{ 7 }\) x 42
= 22 x 6
= 132 sq.m.

ii. Rate of plastering = ₹52 per sq.m.
∴ Total cost = Curved surface area x Rate of plastering
= 132 x 52 = ₹6864
∴ The cost of plastering the well from inside is ₹6864.

Question 9.
The length of a road roller is 2.1 m and its diameter is 1.4 m. For levelling a ground 500 rotations of the road roller were required. How much area of ground was levelled by the road roller? Find the cost of levelling at the rate of ₹ 7 per sq.m.
Given: For road roller,
diameter (d) = 1.4 m,
length (h) = 2.1 m
number of rotations required for levelling the ground = 500,
rate of levelling = ₹ 7 per sq. m.
To find: Area of ground leveled by the road roller and cost of levelling
Solution:
i. Since, area of ground levelled in 1 rotation of road roller = curved surface area of road roller
∴Curved surface area of the road roller = 2πrh
= πdh …[∵ d = 2r]
= \(\frac { 22 }{ 7 }\) x 1.4 x 2.1
= 22 x 0.2 x 2.1
= 9.24 sq.m.

ii. Area of ground levelled in 1 rotation = 9.24 sq.m.
∴Area of ground levelled in 500 rotations = 9.24 x 500
= 4620 sq.m.

iii. Rate of levelling ₹ 7 per sq.m.
∴Total cost = Area of ground levelled x Rate of levelling
= 4620 x 7
= ₹32340
∴ The road roller levels 4620 sq.m. land in 500 rotation, and the cost of levelling is ₹32340.

Maharashtra Board Class 9 Maths Chapter 9 Surface Area and Volume Practice Set 9 Intext Questions and Activities

Question 1.
Curved surface area of cone. (Textbook pg. no. 116)

Circumference of base of the cone = 2πr
As shown in the figure (c), make pieces of the net as small as possible. Join them as shown in the figure (d),. By joining the small pieces of net of the cone, we get a rectangle ABCD approximately.
Total length of AB and CD is 2πr.
∴ length of side AB of rectangle ABCD is πr and length of side CD is also πr.
Length of side BC of rectangle = slant height of cone = l.
Curved surface area of cone is equal to the area of the rectangle.
∴ curved surface area of cone = Area of rectangle = AB x BC = πr x l = πrl

Question 2.
Prepare a cylinder of a card sheet, keeping one of its faces open. Prepare an open cone of card sheet which will have the same base-radius and the same height as that of the cylinder. Pour fine sand in the cone till it just fills up the cone. Empty the cone in the cylinder. Repeat the procedure till the cylinder is just filled up with sand. Note how many coneful of sand is required to fill up the cylinder. (Textbook pg, no 117)

Answer:
To fill the cylinder, three coneful of sand is required.

Question 3.
Finding total surface area of sphere. (Textbook pg, no 120)

i. Take a sweet lime (Mosambe), Cut it into two equal parts.

ii. Take one of the parts. Place its circular face on a paper. Draw its circular border. Copy three more such circles. Again, cut each half of the sweet lime into two equal parts.

iii. Now you get 4 quarters of sweet lime. Separate the peel of a quarter part. Cut it into pieces as small as possible. Try to cover one o’f the circles drawn, by the small pieces. Observe that the circle gets nearly covered.
The activity suggests that,
Curved surface area of a sphere = 4πr²

∴ Curved surface area of a sphere = 4 x Area of a circle

Question 4.
Make a cone and a hemisphere of cardsheet such that radii of cone and hemisphere are equal and height of cone is equal to radius of the hemisphere.
Fill the cone with fine sand. Pour the sand in the hemisphere. How many cones are required to fill the hemisphere completely ? (Textbook pg. no. 121)

Answer:
To fill the hemisphere, two coneful of sand is required.