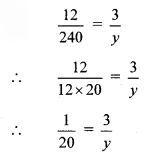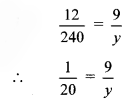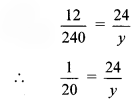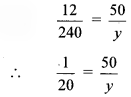Prasanna

Balbharti Maharashtra State Board Class 7 Maths Solutions covers the 7th Std Maths Practice Set 34 Answers Solutions Chapter 8 Algebraic Expressions and Operations on them.

Algebraic Expressions and Operations on them Class 7 Practice Set 34 Answers Solutions Chapter 8

Question 1.
Subtract the second expression from the first.
i. (4xy – 9z); (3xy – 16z)
ii. (5x + 4y + 7z); (x + 2y + 3z)
iii. (14x² + 8xy + 3y²); (26x² – 8xy – 17y²)
iv. (6x² + 7xy + 16y²); (16x² – 17xy)
v. (4x + 16z); (19y – 14z + 16x)
Solution:
i. (4xy – 9z) – (3xy – 16z)
= 4xy – 9z – 3xy + 16z
= (4xy – 3xy) + (16z – 9z)
= xy + 7z

ii. (5x + 4y + 7z) – (x + 2y + 3z)
= 5x + 4y + 7z – x – 2y – 3z
= (5x – x) + (4y – 2y) + (7z – 3z)
= 4x + 2y + 4z

iii. (14x² + 8xy + 3y²) – (26x² – 8xy – 17y²)
= 14x² + 8xy + 3y² – 26x² + 8xy + 17y²
= (14x² – 26x²) + (8xy + 8xy) + (3y² + 17y²)
= -12x² + 16xy + 20y²

iv. (6x² + 7xy + 16y²) – (16x² – 17xy)
= 6x² + 7xy + 16y² – 16x² + 17xy
= (6x² – 16x²) + (7xy + 17xy) + 16y²
= -10x² + 24xy + 16y²

v. (4x + 16z) – (19y— 14z + 16x)
= 4x + 16z – 19y + 14z – 16x
= (4x – 16x) – 19y + (16z + 14z)
= -12x – 19y + 30z

Balbharti Maharashtra State Board Class 7 Maths Solutions covers the 7th Std Maths Practice Set 32  Answers Solutions Chapter 8 Algebraic Expressions and Operations on them.

Algebraic Expressions and Operations on them Class 7 Practice Set 32 Answers Solutions Chapter 8

Question 1.
Classify the following algebraic expressions as monomials, binomials, trinomials or polynomials.
i. 7x
ii. 5y – 7z
iii. 3x³ – 5x² – 11
iv. 1 – 8a – 7a² – 7a³
v. 5m – 3
vi. a
vii. 4
viii. 3y² – 7y + 5
Solution:
i. Monomial
ii. Binomial
iii. Trinomial
iv. Polynomial
v. Binomial
vi. Monomial
vii. Monomial
viii. Trinomial

Balbharti Maharashtra State Board Class 7 Maths Solutions covers the 7th Std Maths Practice Set 33 Answers Solutions Chapter 8 Algebraic Expressions and Operations on them.

Algebraic Expressions and Operations on them Class 7 Practice Set 33 Answers Solutions Chapter 8

Question 1.
Add:
i. 9p + 16q; 13p + 2q
ii. 2a + 6b + 8c; 16a + 13c + 18b
iii. 13x² – 12y²; 6x² – 8y²
iv. 17a²b² + 16c; 28c – 28a²b²
v. 3y² – 10y + 16; 2y – 7
vi. – 3y² + 10y – 16; 7y² + 8
Solution:
i. (9p + 16q) + (13p + 2q)
= (9p + 13p) + (16q + 2q)
= 22p + 18q

ii. (2a + 6b + 8c) + (16a + 13c + 18b)
= (2a + 16a) + (6b + 18b) + (8c + 13c)
= 18a + 24b + 21c

iii. (13x² – 12y²) + (6x² – 8y²)
= (13x² + 6x²) + [(-12y²) + (-8y²)]
= 19x² + (-20y²)
= 19x² – 20y²

iv. (17a²b² + 16c) + (28c – 28a²b²)
= [17a²b² + (-28a²b²)] + (16c + 28c)
= -11a²b² + 44c

v. (3y² – 10y + 16) + (2y – 7)
= 3y² + (-10y + 2y) + (16 – 7)
= 3y² – 8y + 9

vi. (-3y² + 10y – 16) + (7y² + 8)
= (-3y² + 7y²) + (10y) + (-16 + 8)
= 4y² + 10y – 8

Maharashtra Board Class 7 Maths Chapter 8 Algebraic Expressions and Operations on them Practice Set 33 Intext Questions and Activities

Question 1.
Answer the following questions. (Textbook pg. no. 57)

1. 3x + 4y = How many?
2. 3 guavas + 4 mangoes = 7 guavas.
3. 7m – 2n = 5m.

Solution:

1. 3x and 4y are unlike terms. Hence, they cannot be added, further to get a single term.
2. No. Guava and mango are different fruits. Hence, 3 guavas + 4 mangoes & 7 guavas.
3. No. 7m and 2n are unlike terms. Hence, 7m – 2n ≠ 5m.

Balbharti Maharashtra State Board Class 8 Maths Solutions covers the Practice Set 9.2 8th Std Maths Answers Solutions Chapter 9 Discount and Commission.

Practice Set 9.2 8th Std Maths Answers Chapter 9 Discount and Commission

Question 1.
John sold books worth Rs 4500 for a publisher. For this he received 15% commission. Complete the following activity to find the total commission John obtained.
Solution:
Selling price of the books = Rs 4500
Rate of commission = 15%
Commission obtained = 15% of selling price
\(=\frac{[15]}{[100]} \times[4500]\)
= 15 × 45
∴ Commission obtained = 675 Rupees.
∴ The total commission obtained by John is Rs 675.

Question 2.
Rafique sold flowers worth Rs 15,000 by giving 4% commission to the agent. Find the commission he paid. Find the amount received by Rafique.
Solution:
Here, selling price of flowers = Rs 15,000,
Rate of commission = 4%
i. Commission = 4% of selling price
= \(\frac { 4 }{ 100 }\) × 15,000
= 4 x 150
∴ Commission = Rs 600

ii. Amount received by Rafique = selling price – commission
= 15,000 – 600
= Rs 14,400
∴ Rafique paid Rs 600 as commission and the amount received by him was Rs 14,400.

Question 3.
A farmer sold food grains for Rs 9200 through an agent. The rate of commission was 2%. How much amount did the agent get ?
Solution:
Here, selling price of food grains = Rs 9200,
Rate of commission = 2%
Commission = 2% of selling price
= \(\frac { 2 }{ 100 }\) × 9200
= 2 × 92
= Rs 184
∴ The agent got a commission of Rs 184.

Question 4.
Umatai purchased following items from a Khadi – Bhandar.
i. 3 sarees for Rs 560 each.
ii. 6 bottles of honey for Rs 90 each.
On the purchase, she received a rebate of 12%. How much total amount did Umatai pay?
Solution:
Here, number of sarees = 3,
Price of each saree = Rs 560
∴ Cost of 3 sarees = 560 × 3
= Rs 1680 …(i)
Also, number of honey bottles = 6,
Price of each bottle = Rs 90
∴ Cost of 6 honey bottles = 90 × 6
= Rs 540
Total amount of purchase
= cost of 3 sarees + cost of 6 honey bottles
= 1680 + 540 … [From (i) and (ii)]
= Rs 2220 …(iii)
Rate of rebate = 12%
Rebate = 12% of total amount of purchase
= \(\frac { 12 }{ 100 }\) × 2220
= 12 × 22.20
= Rs 266.40 ..(iv)
Amount paid by Umatai
= Total amount of purchase – Rebate
= 2,220 – 266.40 … [From (iii) and (iv)]
= Rs 1953.60
∴ The total amount paid by Umatai is Rs 1953.60.

Question 5.
Use the given information and fill in the boxes with suitable numbers.
Smt. Deepanjali purchased a house for Rs 7,50,000 from Smt. Leelaben through an agent. Agent has charged 2 % brokerage from both of them.
Solution:
i. Smt. Deepanjali paid 7,50,000 × \(\frac { 2 }{ 100 }\)
= 7,500 × 2 = Rs 15,000 brokerage for purchasing the house.

ii. Smt. Leelaben paid brokerage of Rs 15,000

iii. Total brokerage received by the agent is = 15,000 + 15,000 = Rs 30,000

iv. The cost of house Smt. Deepanjali paid is = 7,50,000 + 15,000 = Rs 7,65,000

v. The selling price of house for Smt.Leelaben is = 7,50,000 – 15,000
= Rs 7,35,000

Balbharti Maharashtra State Board Class 8 Maths Solutions covers the Practice Set 8.1 8th Std Maths Answers Solutions Chapter 8 Quadrilateral: Constructions and Types.

Practice Set 8.1 8th Std Maths Answers Chapter 8 Quadrilateral: Constructions and Types

Construct the following quadrilaterals of given measures.

Question 1.
In ∆MORE, l(MO) = 5.8 cm, l(OR) = 4.4 cm, m∠M = 58°, m∠O = 105°, m∠R = 90°.
Solution:

Question 2.
Construct ∆DEFG such that l(DE) = 4.5 cm, l(EF) = 6.5 cm, l(DG) = 5.5 cm, l(DF) = 7.2 cm, l(EG) = 7.8 cm.
Solution:

Question 3.
In ∆ABCD, l(AB) = 6.4 cm, l(BC) = 4.8 cm, m∠A = 70°, m∠B = 50°, m∠C = 140°.
Solution:

Question 4.
Construct ₹LMNO such that
l(LM) = l(LO) = 6 cm,
l(ON) = l(NM) = 4.5 cm, l(OM) = 7.5 cm.
Solution:

Maharashtra Board Class 8 Maths Chapter 8 Quadrilateral: Constructions and Types Practice Set 8.1 Intext Questions and Activities

Question 1.
Construction of a triangle:
Construct the triangles with given measures. (Textbook pg. no. 41)
i. ∆ABC: l(AB) = 5 cm, l(BC) = 5.5, l(AC) = 6 cm.
Solution:

Steps of construction:
Step 1 : As shown in the rough figure, draw seg BC of length 5.5 cm as the base.
Step 2 : By taking a distance of 5 cm on the compass and placing the metal tip of the compass on point B, draw an arc on one side of BC.
Step 3 : By taking a distance 6 cm on the compass and placing the metal tip of the t compass on point C and draw an arc ’ such that it intersects the previous arc. Name the point as A.
Step 4 : Draw segments AB and AC to get the triangle. ∆ABC is the required triangle.

ii. ∆DEF: m∠D = 35°, m∠F = 100°, l(DF) = 4.8 cm.
Solution:

Steps of construction:
Step 1 : As shown in the rough figure, draw seg DF of length 4.8 cm as the base.
Step 2 : Placing the centre of the protractor at point D, mark point P such that m∠PDF = 35°.
Step 3 : Placing the centre of the protractor at point F, mark point Q such that m∠QFD = 100°.
Step 4 : Draw ray DP and ray FQ. Name their point of intersection as E.
∆DEF is required triangle.

iii. ∆MNP: l(MP) = 6.2 cm, l(NP) = 4.5 cm, m∠P = 75°.
Solution:

Steps of construction:
Step 1 : As shown in the rough figure, draw seg PN of length 4.5 cm as the base.
Step 2 : Placing the centre of the protractor at point P, mark point Q such that m∠QPN = 75°.
Step 3 : By taking a distance of 6.2 cm on the compass and placing the metal tip at point P, draw an arc on ray PQ. Name the point as M.
Step 4 : Draw seg MN to get the triangle. ∆MNP is the required triangle.

iv. ∆XYZ: m∠Y = 90°, l(XY) = 4.2 cm, l(XZ) = 7 cm.
Solution:

Steps of construction:
Step 1 : As shown in the rough figure, draw seg XY of 4.2 cm as the base.
Step 2 : Placing the centre of the protractor at point Y, mark point Q such that m∠QYX = 90°.
Step 3 : By taking a distance of 7 cm on the compass and placing the metal tip on point X, draw an arc on ray YQ. Name the point as Z.
Step 4 : Draw seg XZ to get the triangle. ∆XYZ is the required triangle.

Balbharti Maharashtra State Board Class 8 Maths Solutions covers the Practice Set 8.3 8th Std Maths Answers Solutions Chapter 8 Quadrilateral: Constructions and Types.

Practice Set 8.3 8th Std Maths Answers Chapter 8 Quadrilateral: Constructions and Types

Question 1.
Measures of opposite angles of a parallelogram are (3x – 2)° and (50 – x)°. Find the measure of its each angle.
Solution:
Let ₹PQRS be the parallelogram.
m∠Q = (3x – 2)° and m∠S = (50 – x)°

m∠Q = m∠S
…..(i)
[Opposite angles of a parallelogram are congruent]
∴ 3x – 2 = 50 – x
∴ 3x + x = 50 + 2
∴ 4x = 52
∴ x = \(\frac { 52 }{ 4 }\)
∴ x = 13
Now, m∠Q = (3x – 2)°
= (3 x 13 – 2)° = (39 – 2)° = 37°
∴ m∠S = m∠Q = 37° …[From(i)]
m∠P + m∠Q = 180°
….[Adjacent angles of a parallelogram are supplementary]
∴ m∠P + 37° = 180°
∴ m∠P = 180° – 37° = 143°
∴ m∠R = m∠P = 143°
…..[Opposite angles of a parallelogram are congruent]
∴ The measures of the angles of the parallelogram are 37°, 143°, 37° and 143°.

Question 2.
Referring the given figure of a parallelogram, write the answers of questions given below.
i. If l(WZ) = 4.5 cm, then l(XY) = ?
ii. If l(YZ) = 8.2 cm, then l(XW) = ?
iii. If l(OX) = 2.5 cm, then l(OZ) = ?
iv. If l(WO) = 3.3 cm, then l(WY) = ?
v. If m∠WZY = 120°, then m∠WXY = ? and m∠XWZ = ?

Solution:
i. l(WZ) = 4.5 cm … [Given]
l(X Y) = l(WZ) ….[Opposite sides of a parallelogram are congrument ]
∴ l(X Y) = 4.5cm

ii. l(YZ) = 8.2 cm …[Given]
l(XW) = l(YZ)
…[Opposite sides of a parallelogram are congruent]
∴ l(XW) = 8.2cm … [Given]

iii. l(OX) = 2.5 cm …[Given]
l(OZ) = l(OX)
….[Diagonals of a parallelogram bisect each other]
∴ l(OZ) = 2.5cm

iv. l(WO) = 3.3 cm … [Given]
l(WO) = \(\frac { 1 }{ 2 }\) l(WY)
….[Diagonals of a parallelogram bisect each other]
∴ 3.3 = \(\frac { 1 }{ 2 }\) l(WY)
∴ 3.3 x 2 = l(WY)
∴ l(WY) = 6.6cm

v. m∠WZY =120° … [Given]
m∠WXY = m∠WZY
…..[Opposite angles of a parallelogram are congrument]
∴ m∠WXY = 120° …(i)
m∠XWZ + m∠WXY = 180°
….[Adjacent angles of a parallelogram are supplementary]
∴ m∠XWZ + 120° = 180° … [From (i)]
∴ m∠XWZ = 180°- 120°
∴ m∠XWZ = 60°

Question 3.
Construct a parallelogram ABCD such that l(BC) = 7 cm, m∠ABC = 40°, l(AB) = 3 cm
Solution:

Opposite sides of a parallelogram are congruent.
∴ l(AB) = l(CD) = 3cm
l(BC) = l(AD) = 7 cm

Question 4.
Ratio of consecutive angles of a quadrilateral is 1 : 2 : 3 : 4. Find the measure of its each angle. Write with reason, what type of a quadrilateral it is.
Solution:
Let ₹PQRS be the quadrilateral.
Ratio of consecutive angles of a quadrilateral is 1 : 2 : 3 : 4.
Let the common multiple be x.
∴m∠P = x°, m∠Q = 2x°, m∠R = 3x° and m∠S = 4x°
In ₹PQRS,
m∠P + m∠Q + m∠R + m∠S = 360°
…[Sum of the measures of the angles of a quadrilateral is 360°]
∴x° + 2x° + 3x° + 4x° = 360°
∴10 x° = 360°
∴x° = \(\frac { 360 }{ 10 }\)
∴x° = 36°
∴m∠P = x° = 36°

m∠Q = 2x° = 2 × 36° = 72°
m∠R = 3x° = 3 × 36° = 108° and
m∠S = 4x° = 4 × 36° = 144°
∴The measures of the angles of the quadrilateral are 36°, 72°, 108°, 144°.
Here, m∠P + m∠S = 36° + 144° = 180°
Since, interior angles are supplementary,
∴side PQ || side SR
m∠P + m∠Q = 36° + 72° = 108° ≠ 180°
∴side PS is not parallel to side QR.
Since, one pair of opposite sides of the given quadrilateral is parallel.
∴The given quadrilateral is a trapezium.

Question 5.
Construct ₹BARC such that
l(BA) = l(BC) = 4.2 cm, l(AC) = 6.0 cm, l(AR) = l(CR) = 5.6 cm
Solution:

Question 6.
Construct ₹PQRS, such that l(PQ) = 3.5 cm, l(QR) = 5.6 cm, l(RS) = 3.5 cm, m∠Q = 110°, m∠R = 70°. If it is given that ₹PQRS is a parallelogram, which of the given information is unnecessary?
Solution:

1. Since, the opposite sides of a parallelogram are congruent.
   ∴ Either l(PQ) or l(SR) is required.
2. To construct a parallelogram lengths of adjacent sides and measure of one angle is required.
   ∴ Either l(PQ) and m∠Q or l(SR) and m∠R is the unnecessary information given in the question.

Maharashtra Board Class 8 Maths Chapter 8 Quadrilateral: Constructions and Types Practice Set 8.3 Intext Questions and Activities

Question 1.
Draw a parallelogram PQRS. Take two rulers of different widths, place one ruler horizontally and draw lines along its edges. Now place the other ruler in slant position over the lines drawn and draw lines along its edges. We get a parallelogram. Draw the diagonals of it and name the point of intersection as T.

1. Measure the opposite angles of the parallelogram.
2. Measure the lengths of opposite sides.
3. Measure the lengths of diagonals.
4. Measure the lengths of parts of the diagonals made by point T. (Textbook pg. no. 47)

Solution:
[Students should attempt the above activities on their own.]

Question 2.
In the given figure of ₹ABCD, verify with a divider that seg AB ≅ seg CB and seg AD ≅ seg CD. Similarly measure ∠BAD and ∠BCD and verify that they are congruent. (Textbook pg. no. 48)

Solution:
[Students should attempt the above activities on their own.]

Balbharti Maharashtra State Board Class 8 Maths Solutions covers the Practice Set 7.3 8th Std Maths Answers Solutions Chapter 7 Variation.

Practice Set 7.3 8th Std Maths Answers Chapter 7 Variation

Question 1.
Which of the following statements are of inverse variation?
i. Number of workers on a job and time taken by them to complete the job.
ii. Number of pipes of same size to fill a tank and the time taken by them to fill the tank.
iii. Petrol filled in the tank of a vehicle and its cost.
iv. Area of circle and its radius.
Solution:
i. Let, x represent number of workers on a job, and y represent time taken by workers to complete the job.
As the number of workers increases, the time required to complete the job decreases.
∴ \(x \propto \frac{1}{y}\)

ii. Let, n represent number of pipes of same size to fill a tank and t represent time taken by the pipes to fill the tank.
As the number of pipes increases, the time required to fill the tank decreases.
∴ \(\mathrm{n} \propto \frac{1}{\mathrm{t}}\)

iii. Let, p represent the quantity of petrol filled in a tank and c represent the cost of the petrol.
As the quantity of petrol in the tank increases, its cost increases.
∴ p ∝ c

iv. Let, A represent the area of the circle and r represent its radius.
As the area of circle increases, its radius increases.
∴ A ∝ r
∴ Statements (i) and (ii) are examples of inverse variation.

Question 2.
If 15 workers can build a wall in 48 hours, how many workers will be required to do the same work in 30 hours?
Solution:
Let, n represent the number of workers building the wall and t represent the time required.
Since, the number of workers varies inversely with the time required to build the wall.
∴ \(\mathrm{n} \propto \frac{1}{\mathrm{t}}\)
∴ \(\mathrm{n}=\mathrm{k} \times \frac{1}{\mathrm{t}}\)
where k is the constant of variation
∴ n × t = k …(i)
15 workers can build a wall in 48 hours,
i.e., when n = 15, t = 48
∴ Substituting n = 15 and t = 48 in (i), we get
n × t = k
∴ 15 × 48 = k
∴ k = 720
Substituting k = 720 in (i), we get
n × t = k
∴ n × t = 720 …(ii)
This is the equation of variation.
Now, we have to find number of workers required to do the same work in 30 hours.
i.e., when t = 30, n = ?
∴ Substituting t = 30 in (ii), we get
n × t = 720
∴ n × 30 = 720
∴ n = \(\frac { 720 }{ 30 }\)
∴ n = 24
∴ 24 workers will be required to build the wall in 30 hours.

Question 3.
120 bags of half litre milk can be filled by a machine within 3 minutes find the time to fill such 1800 bags?
Solution:
Let b represent the number of bags of half litre milk and t represent the time required to fill the bags.
Since, the number of bags and time required to fill the bags varies directly.
∴ b ∝ t
∴ b = kt …(i)
where k is the constant of variation.
Since, 120 bags can be filled in 3 minutes
i.e., when b = 120, t = 3
∴ Substituting b = 120 and t = 3 in (i), we get
b = kt
∴ 120 = k × 3
∴ k = \(\frac { 120 }{ 3 }\)
∴ k = 40
Substituting k = 40 in (i), we get
b = kt
∴ b = 40 t …(ii)
This is the equation of variation.
Now, we have to find time required to fill 1800 bags
∴ Substituting b = 1800 in (ii), we get
b = 40 t
∴ 1800 = 40 t
∴ t = \(\frac { 1800 }{ 40 }\)
∴ t = 45
∴ 1800 bags of half litre milk can be filled by the machine in 45 minutes.

Question 4.
A car with speed 60 km/hr takes 8 hours to travel some distance. What should be the increase in the speed if the same distance is
to be covered in \(7\frac { 1 }{ 2 }\) hours?
Solution:
Let v represent the speed of car in km/hr and t represent the time required.
Since, speed of a car varies inversely as the time required to cover a distance.
∴ \(v \propto \frac{1}{t}\)
∴ \(\mathbf{v}=\mathbf{k} \times \frac{1}{\mathbf{t}}\)
where, k is the constant of variation.
∴ v × t = k …(i)
Since, a car with speed 60 km/hr takes 8 hours to travel some distance.
i.e., when v = 60, t = 8
∴ Substituting v = 60 and t = 8 in (i), we get
v × t = k
∴ 60 × 8 = t
∴ k = 480
Substituting k = 480 in (i), we get
v × t = k
∴ v × t = 480 …(ii)
This is the equation of variation.
Now, we have to find speed of car if the same distance is to be covered in \(7\frac { 1 }{ 2 }\) hours.
i.e., when t = \(7\frac { 1 }{ 2 }\) = 7.5 , v = ?
∴ Substituting, t = 7.5 in (ii), we get
v × t = 480
∴ v × 7.5 = 480
\(v=\frac{480}{7.5}=\frac{4800}{75}\)
∴ v = 64
The speed of vehicle should be 64 km/hr to cover the same distance in 7.5 hours.
∴ The increase in speed = 64 – 60
= 4km/hr
∴ The increase in speed of the car is 4 km/hr.

Balbharti Maharashtra State Board Class 8 Maths Solutions covers the Practice Set 7.2 8th Std Maths Answers Solutions Chapter 7 Variation.

Practice Set 7.2 8th Std Maths Answers Chapter 7 Variation

Question 1.
The information about number of workers and number of days to complete a work is given in the following table. Complete the table.

Number of workers	30	20	__	10	__
Days	6	9	12		36

Solution:
Let, n represent the number of workers and d represent the number of days required to complete a work.
Since, number of workers and number of days to complete a work are in inverse poportion.
∴ \(\mathbf{n} \propto \frac{1}{\mathrm{d}}\)
∴ \(\mathrm{n}=\mathrm{k} \times \frac{1}{\mathrm{d}}\)
where k is the constant of variation.
∴ n × d = k …(i)

i. When n = 30, d = 6
∴ Substituting n = 30 and d = 6 in (i), we get
n × d = k
∴ 30 × 6 = k
∴ k = 180
Substituting k = 180 in (i), we get
∴ n × d = k
∴ n × d = 180 …(ii)
This is the equation of variation

ii. When d = 12, n = 7
∴ Substituting d = 12 in (ii), we get
n × d = 180
∴ n × 12 = 180
∴ n = \(\frac { 180 }{ 12 }\)
∴ n = 15

iii. When n = 10, d = ?
∴ Substituting n = 10 in (ii), we get
n × d = 180
10 × d = 180
∴ d = \(\frac { 180 }{ 10 }\)
∴ d = 18

iv. When d = 36, n = ?
∴ Substituting d = 36 in (ii), we get
n × d = 180
∴ n × 36 = 180
∴ n = \(\frac { 180 }{ 36 }\)
∴ n = 5

Number of workers	30	20	15	10	5
Days	6	9	12	18	36

Question 2.
Find constant of variation and write equation of variation for every example given below:
i. \(p \propto \frac{1}{q}\) ; if p = 15 then q = 4.
ii. \(z \propto \frac{1}{w}\) ; when z = 2.5 then w = 24.
iii. \(s \propto \frac{1}{t^{2}}\) ; if s = 4 then t = 5.
iv. \(x \propto \frac{1}{\sqrt{y}}\) ; if x = 15 then y = 9.
Solution:
i. \(p \propto \frac{1}{q}\) …[Given]
∴ p = k × \(\frac { 1 }{ q }\)
where, k is the constant of variation.
∴ p × q = k …(i)
When p = 15, q = 4
∴ Substituting p = 15 and q = 4 in (i), we get
p × q = k
∴ 15 × 4 = k
∴ k = 60
Substituting k = 60 in (i), we get
p × q = k
∴ p × q = 60
This is the equation of variation.
∴ The constant of variation is 60 and the equation of variation is pq = 60.

ii. \(z \propto \frac{1}{w}\) …[Given]
∴ z = k × \(\frac { 1 }{ w }\)
where, k is the constant of variation,
∴ z × w = k …(i)
When z = 2.5, w = 24
∴ Substituting z = 2.5 and w = 24 in (i), we get
z × w = k
∴ 2.5 × 24 = k
∴ k = 60
Substituting k = 60 in (i), we get
z × w = k
∴ z × w = 60
This is the equation of variation.
∴ The constant of variation is 60 and the equation of variation is zw = 60.

iii. \(s \propto \frac{1}{t^{2}}\) …[Given]
∴ \(s=k \times \frac{1}{t^{2}}\)
where, k is the constant of variation,
∴ s × t² = k …(i)
When s = 4, t = 5
∴ Substituting, s = 4 and t = 5 in (i), we get
s × t² = k
∴ 4 × (5)² = k
∴ k = 4 × 25
∴ k = 100
Substituting k = 100 in (i), we get
s × t² = k
∴ s × t² = 100
This is the equation of variation.
∴ The constant of variation is 100 and the equation of variation is st² = 100.

iv. \(x \propto \frac{1}{\sqrt{y}}\) …[Given]
∴ \(x=\mathrm{k} \times \frac{1}{\sqrt{y}}\)
where, k is the constant of variation,
∴ x × √y = k …(i)
When x = 15, y = 9
∴ Substituting x = 15 and y = 9 in (i), we get
x × √y = k
∴ 15 × √9 = k
∴ k = 15 × 3
∴ k = 45
Substituting k = 45 in (i), we get
x × √y = k
∴ x × √y = 45 .
This is the equation of variation.
∴ The constant of variation is k = 45 and the equation of variation is x√y = 45.

Question 3.
The boxes are to be filled with apples in a heap. If 24 apples are put in a box then 27 boxes are needed. If 36 apples are filled in a box how many boxes will be needed?
Solution:
Let x represent the number of apples in each box and y represent the total number of boxes required.
The number of apples in each box are varying inversely with the total number of boxes.
∴ \(x \infty \frac{1}{y}\)
∴ \(x=k \times \frac{1}{y}\)
where, k is the constant of variation,
∴ x × y = k …(i)
If 24 apples are put in a box then 27 boxes are needed.
i.e., when x = 24, y = 27
∴ Substituting x = 24 and y = 27 in (i), we get
x × y = k
∴ 24 × 27 = k
∴ k = 648
Substituting k = 648 in (i), we get
x × y = k
∴ x × y = 648 …(ii)
This is the equation of variation.
Now, we have to find number of boxes needed
when, 36 apples are filled in each box.
i.e., when x = 36,y = ?
∴ Substituting x = 36 in (ii), we get
x × y = 648
∴ 36 × y = 648
∴ y = \(\frac { 648 }{ 36 }\)
∴ y = 18
∴ If 36 apples are filled in a box then 18 boxes are required.

Question 4.
Write the following statements using symbol of variation.

1. The wavelength of sound (l) and its frequency (f) are in inverse variation.
2. The intensity (I) of light varies inversely with the square of the distance (d) of a screen from the lamp.

Solution:

1. \(l \propto \frac{1}{\mathrm{f}}\)
2. \(\mathrm{I} \propto \frac{1}{\mathrm{d}^{2}}\)

Question 5.
\(x \propto \frac{1}{\sqrt{y}}\) and when x = 40 then y = 16. If x = 10, find y.
Solution:
\(x \propto \frac{1}{\sqrt{y}}\)
∴ \(x=\mathrm{k} \times \frac{1}{\sqrt{y}}\)
where, k is the constant of variation.
∴ x × √y = k …(i)
When x = 40, y = 16
∴ Substituting x = 40 andy = 16 in (i), we get
x × √y = k
∴ 40 × √16 = k
∴ k = 40 × 4
∴ k = 160
Substituting k = 160 in (i), we get
x × √y = k
∴ x × √y = 160 …(ii)
This is the equation of variation.
When x = 10,y = ?
∴ Substituting, x = 10 in (ii), we get
x × √y = 160
∴ 10 × √y = 160
∴ √y = \(\frac { 160 }{ 10 }\)
∴ √y = 16
∴ y = 256 … [Squaring both sides]

Question 6.
x varies inversely as y, when x = 15 then y = 10, if x = 20, then y = ?
Solution:
Given that,
\(x \propto \frac{1}{\sqrt{y}}\)
∴ \(x=\mathrm{k} \times \frac{1}{\sqrt{y}}\)
where, k is the constant of variation.
∴ x × y = k …(i)
When x = 15, y = 10
∴ Substituting, x = 15 and y = 10 in (i), we get
x × y = k
∴ 15 × 10 = k
∴ k = 150
Substituting, k = 150 in (i), we get
x × y = k
∴ x × y = 150 …(ii)
This is the equation of variation.
When x = 20, y = ?
∴ substituting x = 20 in (ii), we get
x × y = 150
∴ 20 × y = 150
∴ y = \(\frac { 150 }{ 20 }\)
∴ y = 7.5

Balbharti Maharashtra State Board Class 8 Maths Solutions covers the Practice Set 7.1 8th Std Maths Answers Solutions Chapter 7 Variation.

Practice Set 7.1 8th Std Maths Answers Chapter 7 Variation

Question 1.
Write the following statements using the symbol of variation.

1. Circumference (c) of a circle is directly proportional to its radius (r).
2. Consumption of petrol (l) in a car and distance traveled by that car (d) are in direct variation.

Solution:

1. c ∝ r
2. l ∝ d

Question 2.
Complete the following table considering that the cost of apples and their number are in direct variation.

Number of apples (x)	1	4	__	12	__
Cost of apples (y)	8	32	56	__	160

Solution:
The cost of apples (y) and their number (x) are in direct variation.
∴y ∝ x
∴y = kx …(i)
where k is the constant of variation

i. When, x = 1, y = 8
∴ Substituting, x = 1 and y = 8 in (i), we get y = kx
∴ 8 = k × 1
∴ k = 8
Substituting k = 8 in (i), we get
y = kx
∴ y = 8x …(ii)
This the equation of variation

ii. When,y = 56, x = ?
∴ Substituting y = 56 in (ii), we get
y = 8x
∴ 56 = 8x
∴ x = \(\frac { 56 }{ 8 }\)
∴ x = 7

iii. When, x = 12, y = ?
∴ Substituting x = 12 in (ii), we get
y = 8x
∴ y = 8 × 12
∴ y = 96

iv. When, y = 160, x = ?
∴ Substituting y = 160 in (ii), we get
y = 8x
∴ 160 = 8x
∴ x = \(\frac { 160 }{ 8 }\)
∴ x = 20

Number of apples (x)	1	4	7	12	20
Cost of apples (y)	8	32	56	96	160

Question 3.
If m ∝ n and when m = 154, n = 7. Find the value of m, when n = 14.
Solution:
Given that,
m ∝ n
∴ m = kn …(i)
where k is constant of variation.
When m = 154, n = 7
∴ Substituting m = 154 and n = 7 in (i), we get
m = kn
∴ 154 = k × 7
∴ \(k=\frac { 154 }{ 7 }\)
∴ k = 22
Substituting k = 22 in (i), we get
m = kn
∴ m = 22n …(ii)
This is the equation of variation.
When n = 14, m = ?
∴ Substituting n = 14 in (ii), we get
m = 22n
∴ m = 22 × 14
∴ m = 308

Question 4.
If n varies directly as m, complete the following table.

m	3	5	6.5	__	1.25
n	12	20	__	28	__

Solution:
Given, n varies directly as m
∴ n ∝ m
∴ n = km …(i)
where, k is the constant of variation

i. When m = 3, n = 12
∴ Substituting m = 3 and n = 12 in (i), we get
n = km
∴ 12 = k × 3
∴ \(k=\frac { 12 }{ 3 }\)
∴ k = 4
Substituting, k = 4 in (i), we get
n = km
∴ n = 4m …(ii)
This is the equation of variation.

ii. When m = 6.5, n = ?
∴ Substituting, m = 6.5 in (ii), we get
n = 4m
∴ n = 4 × 6.5
∴ n = 26

iii. When n = 28, m = ?
∴ Substituting, n = 28 in (ii), we get
n = 4m
∴ 28 = 4m
∴ 28 = 4m
∴ \(m=\frac { 28 }{ 4 }\)
∴ m = 7

iv. When m = 1.25, n = ?
∴ Substituting m = 1.25 in (ii), we get
n = 4m
∴ n = 4 × 1.25
∴ n = 5

m	3	5	6.5	7	1.25
n	12	20	26	28	5

Question 5.
y varies directly as square root of x. When x = 16, y = 24. Find the constant of variation and equation of variation.
Solution:
Given, y varies directly as square root of x.
∴ y ∝ √4x
∴ y = k √x …(i)
where, k is the constant of variation.
When x = 16 ,y = 24.
∴ Substituting, x = 16 and y = 24 in (i), we get
y = k√x
∴24 = k√16
∴24 = 4k
∴ \(k=\frac { 24 }{ 4 }\)
∴ k = 6
Substituting k = 6 in (i), we get
y = k√x
∴ y = 6√x
This is the equation of variation
∴ The constant of variation is 6 and the equation of variation is y = 6√x .

Question 6.
The total remuneration paid to laborers, employed to harvest soybean is in direct variation with the number of laborers. If remuneration of 4 laborers is Rs 1000, find the remuneration of 17 laborers.
Solution:
Let, m represent total remuneration paid to laborers and n represent number of laborers employed to harvest soybean.
Since, the total remuneration paid to laborers, is in direct variation with the number of laborers.
∴ m ∝ n
∴ m = kn …(i)
where, k = constant of variation
Remuneration of 4 laborers is Rs 1000.
i. e., when n = 4, m = Rs 1000
∴ Substituting, n = 4 and m = 1000 in (i), we get m = kn
∴ 1000 = k × 4
∴ \(k=\frac { 1000 }{ 4 }\)
∴ k = 250
Substituting, k = 250 in (i), we get
m = kn
∴ m = 250 n …(ii)
This is the equation of variation
Now, we have to find remuneration of 17 laborers.
i. e., when n = 17, m = ?
∴ Substituting n = 17 in (ii), we get
m = 250 n
∴ m = 250 × 17
∴ m = 4250
∴ The remuneration of 17 laborers is Rs 4250.

Maharashtra Board Class 8 Maths Chapter 7 Variation Practice Set 7.1 Intext Questions and Activities

Question 1.
If the rate of notebooks is Rs 240 per dozen, what is the cost of 3 notebooks?
Also find the cost of 9 notebooks, 24 notebooks and 50 notebooks and complete the following table. (Textbook pg. no. 35)

Number of notebooks (x)	12	3	9	24	50	1
Cost (In Rupees) (y)	240	__	__	__	__	20

Solution:
As the number of notebooks increases their cost also increases.
∴ Number of notebooks and cost of notebooks are in direct proportion.

i.

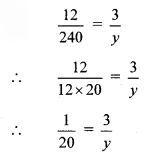
∴ y = 3 × 20
∴ y = 60

ii.

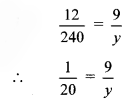
∴ y = 9 × 20
∴ y = 180

iii.

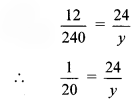
∴ y = 24 × 20
∴ y = 480

iv.

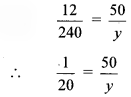
∴ y = 50 × 20
∴ y = 1000

Number of notebooks (x)	12	3	9	24	50	1
Cost (In Rupees) (y)	240	60	180	480	1000	20

Balbharti Maharashtra State Board Class 8 Maths Solutions covers the Practice Set 6.4 8th Std Maths Answers Solutions Chapter 6 Factorisation of Algebraic Expressions.

Practice Set 6.4 8th Std Maths Answers Chapter 6 Factorisation of Algebraic Expressions

Question 1.
Simplify:
i. \(\frac{m^{2}-n^{2}}{(m+n)^{2}} \times \frac{m^{2}+m n+n^{2}}{m^{3}-n^{3}}\)
ii. \(\frac{a^{2}+10 a+21}{a^{2}+6 a-7} \times \frac{a^{2}-1}{a+3}\)
iii. \(\frac{8 x^{3}-27 y^{3}}{4 x^{2}-9 y^{2}}\)
iv. \(\frac{x^{2}-5 x-24}{(x+3)(x+8)} \times \frac{x^{2}-64}{(x-8)^{2}}\)
v. \(\frac{3 x^{2}-x-2}{x^{2}-7 x+12} \div \frac{3 x^{2}-7 x-6}{x^{2}-4}\)
vi. \(\frac{4 x^{2}-11 x+6}{16 x^{2}-9}\)
vii. \(\frac{a^{3}-27}{5 a^{2}-16 a+3} \div \frac{a^{2}+3 a+9}{25 a^{2}-1}\)
viii. \(\frac{1-2 x+x^{2}}{1-x^{3}} \times \frac{1+x+x^{2}}{1+x}\)
Solution:
i. \(\frac{m^{2}-n^{2}}{(m+n)^{2}} \times \frac{m^{2}+m n+n^{2}}{m^{3}-n^{3}}\)

ii. \(\frac{a^{2}+10 a+21}{a^{2}+6 a-7} \times \frac{a^{2}-1}{a+3}\)

iii. \(\frac{8 x^{3}-27 y^{3}}{4 x^{2}-9 y^{2}}\)

iv. \(\frac{x^{2}-5 x-24}{(x+3)(x+8)} \times \frac{x^{2}-64}{(x-8)^{2}}\)

v. \(\frac{3 x^{2}-x-2}{x^{2}-7 x+12} \div \frac{3 x^{2}-7 x-6}{x^{2}-4}\)

vi. \(\frac{4 x^{2}-11 x+6}{16 x^{2}-9}\)

vii. \(\frac{a^{3}-27}{5 a^{2}-16 a+3} \div \frac{a^{2}+3 a+9}{25 a^{2}-1}\)

viii. \(\frac{1-2 x+x^{2}}{1-x^{3}} \times \frac{1+x+x^{2}}{1+x}\)