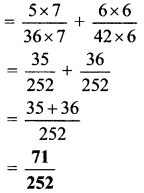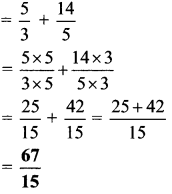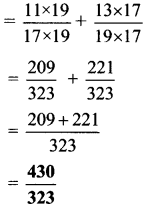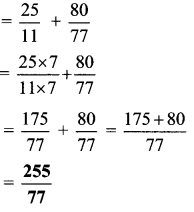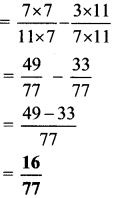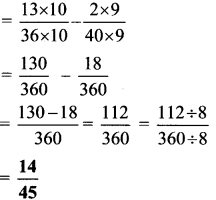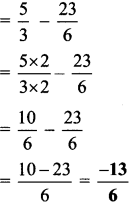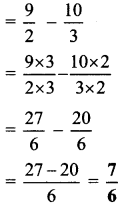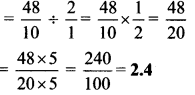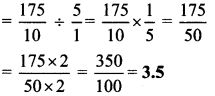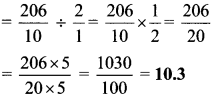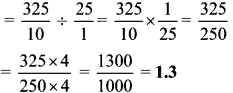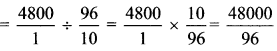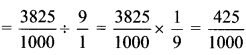Balbharti Maharashtra State Board Class 7 Maths Solutions covers the 7th Std Maths Practice Set 22 Answers Solutions Chapter 5 Operations on Rational Numbers.
Operations on Rational Numbers Class 7 Practice Set 22 Answers Solutions Chapter 5
Question 1.
Carry out the following additions of rational numbers:
i. \(\frac{5}{36}+\frac{6}{42}\)
ii. \(1 \frac{2}{3}+2 \frac{4}{5}\)
iii. \(\frac{11}{17}+\frac{13}{19}\)
iv. \(2 \frac{3}{11}+1 \frac{3}{77}\)
Solution:
i. \(\frac{5}{36}+\frac{6}{42}\)
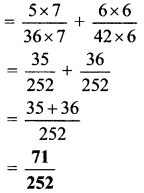
ii. \(1 \frac{2}{3}+2 \frac{4}{5}\)
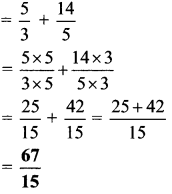
iii. \(\frac{11}{17}+\frac{13}{19}\)
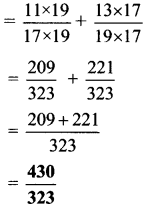
iv. \(2 \frac{3}{11}+1 \frac{3}{77}\)
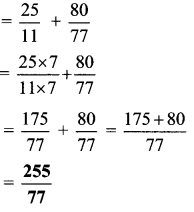
Question 2.
Carry out the following subtractions involving rational numbers.
i. \(\frac{7}{11}-\frac{3}{7}\)
ii. \(\frac{13}{36}-\frac{2}{40}\)
iii. \(1 \frac{2}{3}-3 \frac{5}{6}\)
iv. \(4 \frac{1}{2}-3 \frac{1}{3}\)
Solution:
i. \(\frac{7}{11}-\frac{3}{7}\)
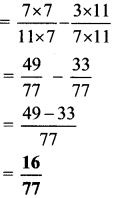
ii. \(\frac{13}{36}-\frac{2}{40}\)
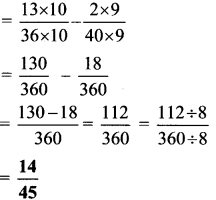
iii. \(1 \frac{2}{3}-3 \frac{5}{6}\)
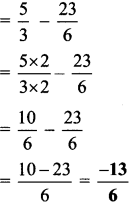
iv. \(4 \frac{1}{2}-3 \frac{1}{3}\)
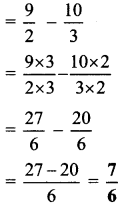
Question 3.
Multiply the following rational numbers.
i. \(\frac{3}{11} \times \frac{2}{5}\)
ii. \(\frac{12}{5} \times \frac{4}{15}\)
iii. \(\frac{(-8)}{9} \times \frac{3}{4}\)
iv. \(\frac{0}{6} \times \frac{3}{4}\)
Solution:
i. \(\frac{3}{11} \times \frac{2}{5}\)
\(=\frac{3 \times 2}{11 \times 5}=\frac{6}{55}\)
ii. \(\frac{12}{5} \times \frac{4}{15}\)
\(=\frac{4}{5} \times \frac{4}{5}=\frac{4 \times 4}{5 \times 5}=\frac{16}{25}\)
iii. \(\frac{(-8)}{9} \times \frac{3}{4}\)
\(=\frac{(-2)}{3} \times \frac{1}{1}=\frac{-2}{3}\)
iv. \(\frac{0}{6} \times \frac{3}{4}\)
\(=0 \times \frac{3}{4}=0\)
Question 4.
Write the multiplicative inverse of.
i. \(\frac{2}{5}\)
ii. \(\frac{-3}{8}\)
iii. \(\frac{-17}{39}\)
iv. 7
v. \(-7 \frac{1}{3}\)
Solution:
i. \(\frac{5}{2}\)
ii. \(\frac{-8}{3}\)
iii. \(\frac{-39}{17}\)
iv. \(\frac {1}{7}\)
v. \(\frac {-3}{22}\)
Question 5.
Carry out the divisions of rational numbers:
i. \(\frac{40}{12} \div \frac{10}{4}\)
ii. \(\frac{-10}{11} \div \frac{-11}{10}\)
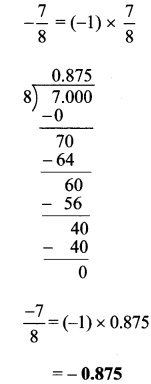
iii. \(\frac{-7}{8} \div \frac{-3}{6}\)
iv. \(\frac{2}{3} \div(-4)\)
v. \(2 \frac{1}{5} \div 5 \frac{3}{6}\)
vi. \(\frac{-5}{13} \div \frac{7}{26}\)
vii. \(\frac{9}{11} \div(-8)\)
viii. \(5 \div \frac{2}{5}\)
Solution:
i. \(\frac{40}{12} \div \frac{10}{4}\)
\(=\frac{40}{12} \times \frac{4}{10}=\frac{4}{3}\)
ii. \(\frac{-10}{11} \div \frac{-11}{10}\)
\(=\frac{-10}{11} \times \frac{-10}{11}=\frac{100}{121}\)
iii. \(\frac{-7}{8} \div \frac{-3}{6}\)
\(=\frac{-7}{8} \times \frac{-6}{3}=\frac{-7}{4} \times \frac{-3}{3}=\frac{7}{4}\)
iv. \(\frac{2}{3} \div(-4)\)
\(=\frac{2}{3} \times \frac{-1}{4}=\frac{1}{3} \times \frac{-1}{2}=\frac{-1}{6}\)
v. \(2 \frac{1}{5} \div 5 \frac{3}{6}\)
\(=\frac{11}{5} \div \frac{33}{6}=\frac{11}{5} \times \frac{6}{33}=\frac{1}{5} \times \frac{6}{3}=\frac{2}{5}\)
vi. \(\frac{-5}{13} \div \frac{7}{26}\)
\(=\frac{-5}{13} \times \frac{26}{7}=\frac{-10}{7}\)
vii. \(\frac{9}{11} \div(-8)\)
\(=\frac{9}{11} \times \frac{-1}{8}=\frac{-9}{88}\)
viii. \(5 \div \frac{2}{5}\)
\(=\frac{5}{1} \times \frac{5}{2}=\frac{25}{2}\)
Maharashtra Board Class 7 Maths Chapter 5 Operations on Rational Numbers Practice Set 22 Intext Questions and Activities
Question 1.
Complete the table given below. (Textbook pg. no. 34)
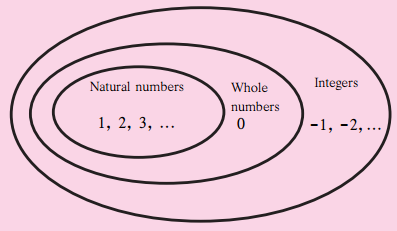
| -3 | \(\frac {3}{5}\) | -17 | \(\frac { -5 }{ 11 }\) | 5 |
| Natural Numbers | x | | | | ✓ |
| Integers | ✓ | | | | |
| Rational Numbers | ✓ | | | | |
Solution:
| -3 | \(\frac {3}{5}\) | -17 | \(\frac { -5 }{ 11 }\) | 5 |
| Natural Numbers | x | x | x | x | ✓ |
| Integers | ✓ | x | ✓ | x | ✓ |
| Rational Numbers | ✓ | ✓ | ✓ | ✓ | ✓ |
Question 2.
Discuss the characteristics of various groups of numbers in class and complete the table below. In front of each group, write the inference you make after carrying out the operations of addition, subtraction, multiplication and division, using a (✓) or a (x).
Remember that you cannot divide by zero. (Textbook pg. no. 35)
| Group of Numbers | Addition | Subtraction | Multiplication | Division |
| Natural Numbers | ✓ | x
(7- 10 =-3) | ✓ | x
(3÷5=\(\frac { 3 }{ 5 }\)) |
| Integers | | | | |
| Rational Numbers | | | | |
Solution:
| Group of Numbers | Addition | Subtraction | Multiplication | Division |
| Natural Numbers | ✓ | x
(7- 10 =-3) | ✓ | x
(3÷5=\(\frac { 3 }{ 5 }\)) |
| Integers | ✓ | ✓ | ✓ | x
(4÷9=\(\frac { 4 }{ 9 }\)) |
| Rational Numbers | ✓ | ✓ | ✓ | ✓ |
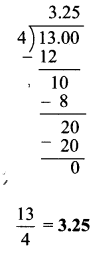
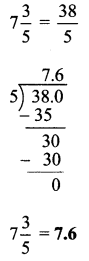




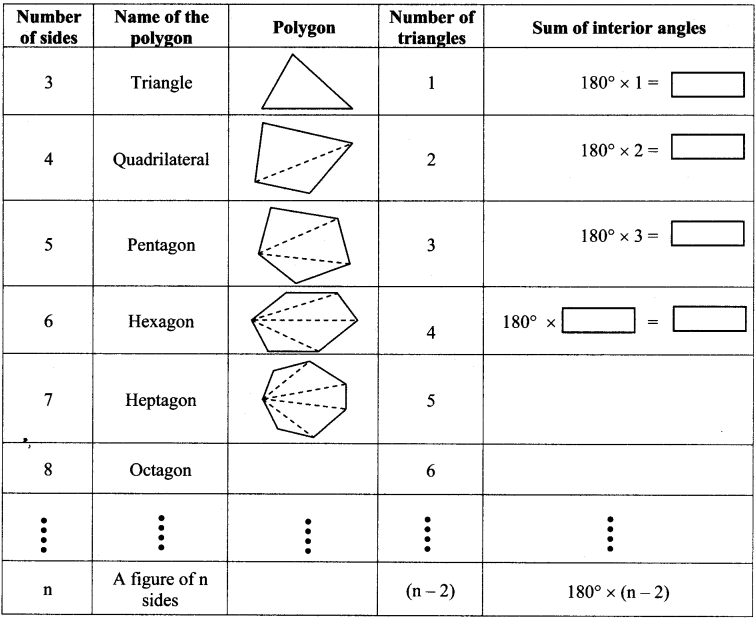
 , 180° x 6 = 1080°
, 180° x 6 = 1080°