Maharashtra Board Class 12 Physics Important Questions Chapter 7 Wave Optics

Balbharti Maharashtra State Board 12th Physics Important Questions Chapter 7 Wave Optics Important Questions and Answers.

Maharashtra State Board 12th Physics Important Questions Chapter 7 Wave Optics

Question 1.
Name the various theories of the nature of light.
Answer:
The various theories of the nature of light from the 17th century to the modern times are

1. Descartes’ corpuscular theory of light (1637)
2. Newton’s corpuscular theory (1666)
3. Huygens’ wave theory of light propagation (1678), modified, verified and put on a firm mathematical base by Young, Fraunhofer, Fresnel and Kirchhoff (in the 1800s)
4. Maxwell’s electromagnetic theory (1865)
5. the light quantum, i.e., the photon model of the modern quantum theory by Planck (1900) and Einstein (1905).

Question 2.
State the postulates of Newton’s corpuscular theory of light.
Answer:
Sir Isaac Newton developed the corpuscular theory of light proposed by Rene’ Descartes (1596-1650), French philosopher and mathematician. The theory assumed that light consists of a stream of corpuscles emitted by a luminous source.
Postulates of Newton’s corpuscular theory of light:

1. Light corpuscles are minute, light and perfectly elastic particles.
2. A luminous source emits light corpuscles in all directions which then travel at high speed in straight lines in a given medium.
3. The constituent colours of white light are due to different sizes of the corpuscles.
4. The light corpuscles stimulate the sense of sight on their impact on the retina of the eye.
5. A reflective surface exerts a force of repulsion normal to the surface on the light corpuscles when they strike the surface.
6. A transparent medium exerts a force of attraction normal to the surface on the light corpuscles striking the surface. This force is different for different mediums.

Notes :

1. A consequence of the assumption (6) is that, according to the corpuscular theory, the speed of light in a denser medium is greater than that in air and has different values for different mediums.
2. It was known from earliest recorded times that when light is incident on the surface of glass or water, it is partly reflected and partly transmitted, simultaneously. To explain this, Newton postulated that the corpuscles must have fits of easy reflection and fits of easy transmission and must pass periodically from one state to the other.

Question 3.
State the drawbacks of Newton’s corpuscular theory of light.
Answer:
Drawbacks of Newton’s corpuscular theory of light:

1. The theory predicted that the speed of light in a
   denser medium should be greater than that in air. This was disproved when experiment showed that the speed of light in water is less than that in air (carried out in 1850 by French physicist Jean Bernard Leon Foucault). ,
2. The theory could not satisfactorily explain the phenomenon of polarization and the simultaneousness of reflection and refraction.
3. The corpuscular theory failed to explain the phenomena of diffraction and interference.
4. There was no basis for the hypothesis that the constituent colours of white light are due to different sized corpuscles.

Question 4.
What is a ray of light?
Answer:
A ray of light is the path along which light energy is transmitted from one point to another in an optical system.

Question 5.
What is meant by ray optics or geometrical optics?
Answer:
The formation of

1. shadows, and
2. images by mirrors and lenses can be explained by assuming that light propagates in a straight line in terms of rays. The study of optical phenomena under this assumption is called ray optics. It is also called geometrical optics as geometry is used in this study.

Question 6.
Give a brief account of Huygens’ wave theory of light. State its merits and demerits.
Answer:
Huygens’ wave theory of light [Christiaan Huygens (1629-95), Dutch physicist] :

1. Light emitted by a source propagates in the form of waves. Huygens’ original theory assumed them to be longitudinal waves.
2. In a homogeneous isotropic medium, light from a point source spreads by spherical waves.
3. It was presumed that a wave motion needed a medium for its propagation. Hence, the theory postulated a medium called luminiferous ether that exists everywhere, in vacuum as well as in transparent bodies. Ether had to be assigned some extraordinary properties, a high modulus of elasticity (to account for the high speed of light), zero density (so that it offers no resistance to planetary motion) and perfect transparency.
4. The different colours of light are due to different wavelengths.

Merits :

1. Huygens’ wave theory satisfactorily explains reflection and refraction as well as their simultaneity.
2. In explaining refraction, the theory concludes that the speed of light in a denser medium is less than that in a rarer medium, in agreement with experimental findings.
3. The theory was later used by Young in 1800-04, Fraunhofer and Fresnel in 1814 to satisfactorily explain interference, diffraction and rectilinear propagation of light. The phenomenon of polarization could also be explained considering the light waves to be transverse.

Demerits :

1. It was found much later that the hypothetical medium, luminiferous ether, has no experimental basis. Einstein discarded the idea of ether completely in 1905.
2. Phenomena like absorption and emission of light, photoelectric effect and Compton effect, cannot be explained on the basis of the wave theory.

[Note: To decide between the particle and wave theories of light, Dominique Francois Jean Arago (1786-1853), French physicist, suggested the measurement of the speed of light in air and water. The experiment was performed in 1850 by Leon Foucault (1819-68), French physicist, using Arago’s experimental equipment. He found that the speed of light in water is less than that in air.]

Question 7.
What is meant by wave optics?
Answer:
It is not possible to explain certain phenomena of light, such as interference, diffraction and polarization, with the help of ray optics (geometrical optics). The branch of optics which uses wave nature of light to explain these optical phenomena is called wave optics.

Question 8.
What was Maxwell’s concept of light?
Answer:
In 1865, James Clerk Maxwell developed a mathematical theory on the intimate relationship between electricity and magnetism. His theory predicted light to be a high-frequency transverse electromagnetic wave in ether. Electric and magnetic fields in the wave vary periodically in space and time at right angles to each other and to the direction of propagation of the wave.

The speed of the electromagnetic waves in a medium, as calculated on the basis of Maxwell’s theory, was experimentally found to be equal to the measured speed of light in that medium. Maxwell’s electromagnetic theory of light, with addition by others till 1896, could account for all the known phenomena regarding the propagation (or transmission) of light through space and through matter.

Question 9.
What is the photon model or quantum hypothesis of light ?
Answer:
To explain the interaction of light and matter (as in the emission or absorption of radiation), Max Planck, in 1900, and Einstein, in 1905, hypothesized light as concentrated or localized packets of energy. Such an energy packet is called a quantum of energy, which was given the name photon much later, in 1926, by Frithiof Wolfers and Gilbert Newton Lewis. For a radiation of frequency v, a quantum of energy is hv, where h is a universal constant, now called Planck’s constant.

[Note : ‘Localisation’ of energy in a region gives light its particle nature while frequency is a wave characteristic. The complementary properties of particle and wave of light quanta are reconciled as follows : light propagates as wave but interacts with matter as particle.]

Question 10.
Give a brief account of the wave nature of light.
Answer:

1. Light is a transverse, electromagnetic wave.
2. A light wave consists of oscillating electric and magnetic fields that are perpendicular to each other and also perpendicular to the direction of propagation of the wave.
3. Like all other electromagnetic waves, light waves do not require any material medium as they can travel even through vacuum.
4. In a material medium, the speed of light depends on the refractive index of the medium, which, in turn depends on the permeability and permittivity of the medium.

Question 11.
Define absolute refractive index of a medium.
Answer:
The absolute refractive index of a medium is defined as the ratio of the speed of light in vacuum to the speed of light in the medium.
[Note : Absolute refractive index of a medium (n) =

The absolute refractive index of vacuum is 1 (by definition) and that of air is greater than 1, but very nearly equal to 1.]

Question 12.
State the characteristics of the electromagnetic waves.
Answer:

1. The electromagnetic waves are transverse in nature as they propagate by oscillating electric and magnetic fields that are perpendicular to each other and also perpendicular to the direction of propagation of the wave.
2. These waves do not require any material medium for their propagation, i.e., they can travel even through vacuum.
3. The wavelength of the electromagnetic waves ranges from very small (< 1 fm) to very large (> 1 km). The waves are classified in the order of increasing wavelength as γ-rays, X rays, ultraviolet, visible, infrared, microwave and radio waves.
4. In vacuum, the speed of electromagnetic waves does not depend on the frequency of the wave. But, in a material medium, it depends on the frequency. For a given frequency, the speed is different in different mediums.
   [Note : 1 fm (femtometre) = 10^-15 m]

Question 13.
Define and explain :
(a) a wave normal
(b) a ray of light.
Answer:
(a) Wavenormal: A wave normal at a point on a wavefront is defined as a line drawn perpendicular to the wavefront in the direction of propagation of the wavefront.

In a homogeneous isotropic medium, a wavefront moves parallel to itself. Thus, at any point in the medium, the direction in which the wavefront moves is always perpendicular to the wavefront at that point. This direction is given by the wave normal at that point.

(b) Ray of light: The direction in which light is propagated is called a ray of light.

This term (ray of light) is also used to mean a narrow beam of light waves. Only in a homogeneous isotropic medium is a ray of light the same as a wave normal. For spherical wavefronts spreading out from a point source, the rays are radially divergent. The rays corresponding to a plane’ wavefront form a parallel beam.

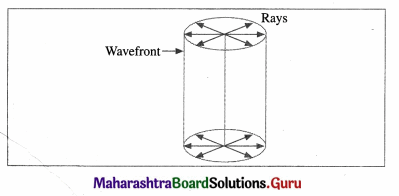
Question 14.
What is a cylindrical wavefront? Draw the corresponding diagram.
Answer:
Cylindrical wavefront: An extended linear source, such as an aperture in the form of a narrow slit, gives rise to cylindrical wavefronts. All the points equidistant from the source lie on the curved surface of a cylinder. Thus, the shape of the wavefront is cylindrical.

Question 15.
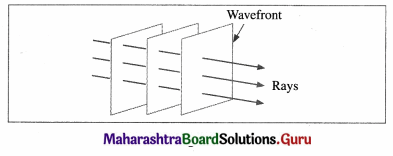
What is a plane wavefront? Draw the corresponding diagram.
Answer:
Plane wavefront: It may be treated as a part of a spherical or cylindrical wavefront at a very great distance from the source, such that the wavefront has a negligible curvature.

Question 16.
Draw a neat labelled diagram illustrating spherical wavefronts corresponding to a diverging beam of light.
Answer:

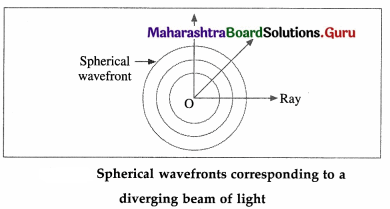
Note : Lenses can be used to obtain

1. a converging beam of light
2. a diverging beam of light.

Question 17.
State Huygens’ principle.
Answer:
Huygens’ principle : Every point on a wavefront acts as a secondary source of light and sends out secondary wavelets in all directions. The secondary wavelets travel with the speed of light in the medium. These wavelets are effective only in the forward direction and not in the backward direction. At any instant, the forward-going envelope or the surface of tangency to these wavelets gives the position of the new wavefront at that instant.

Question 18.
Explain the construction and propagation of a plane wavefront using Huygens’ principle.
Answer:
Huygens’ construction nf a plane wavefront: A plane wavefront may be treated as a part of a spherical or cylindrical wave at a very great distance from a point source or an extended source, such that the wavefront has a negligible curvature. Let A, B, C, D, …, be points on a plane wavefront in a homogeneous isotropic medium in which the speed of light, taken to be monochromatic, is v.

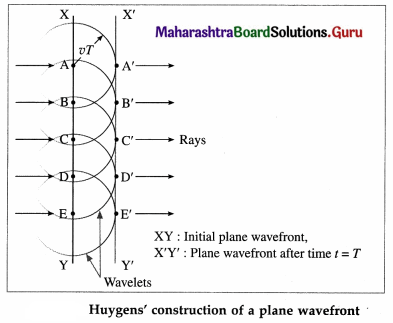
In a time, t = T, secondary wavelets with points A, B, C, D,…, as secondary sources travel a distance vT. To find the position of the wavefront after a time t = T, we draw spheres of radii vT with A, B, C,…, as centres. The envelope or the surface of tangency to these spheres is a plane A’B’C’. This plane, the new wavefront, is at a perpendicular distance vT from the original wavefront in the direction of propagation of the wave. Thus, in an isotropic medium, plane wavefronts are propagated as planes.

Question 19.
Explain the construction and propagation of a spherical wavefront using Huygens’ principle.
Answer:
Huygens’ construction of a spherical wavefront: Consider a point source of monochromatic light S in a homogeneous isotropic medium. The light waves travel with the same speed v in all directions. After time f, the wave will reach all the points which are at a distance vt from S. This is spherical wavefront XY. Let, A, B, C, …,, be points on this wavefront.

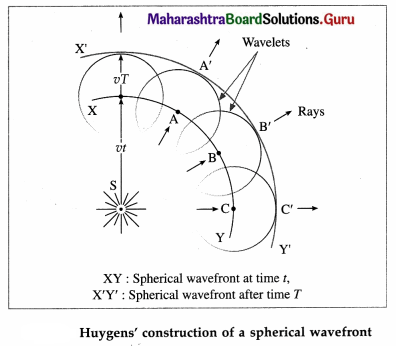
To find the new wavefront after time T, we draw spheres of radius vT with A, B, C,…, as centres. The envelope or the surface of tangency of these spheres is the surface A’B’C’. This is the new spherical wavefront X’Y’. Thus, in an isotropic medium, spherical wavefronts are propagated as concentric spheres.

Question 20.
Suppose a parallel beam of monochromatic light is incident normally at a boundary separating two media. Explain what happens to the wavelength and frequency of the light as it propagates from medium 1 to medium 2. What happens when the medium 1 is vacuum ?
Answer:
Consider a parallel beam of monochromatic light incident normally on interface PQ separating a rarer medium (medium 1) and a denser medium (medium 2).

The three successive wavefronts AB, CD and EF are separated by a distance λ₁, the wavelength of light in first medium. The corresponding three wavefronts after refraction, are A’B’, C’D’ and E’F’. Due to the denser medium, the speed of light reduces and hence the wavefronts cover a less distance than that covered in the same time in the first medium. Thus, the wavefronts are comparitively more closely spaced than in the first medium. This distance between successive wavefronts is λ₂, the wavelength of light in the second medium. Thus, λ₂ is less than λ₁,. To find the relation between λ₁ and λ₂, let us consider the wavefront AB reaching

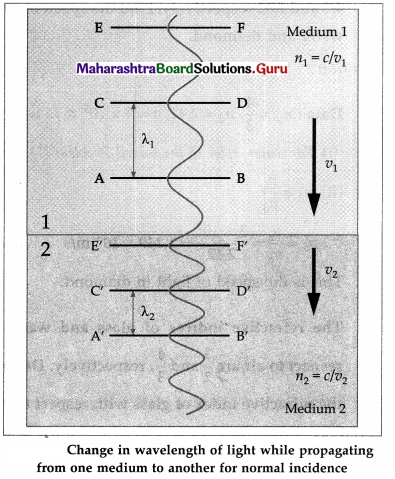
PQ at time t = 0. The next wavefront CD, separated from AB by distance λ₁, will reach PQ at time t = T. Let v₁ and v₂ be the speeds of light in medium 1 and medium 2 respectively. T is the time during which light covers distance λ₁ in medium 1 and λ₂ in medium 2.

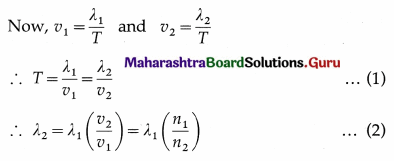
This shows how the wavelength of light changes in refraction.

If the first medium is vacuum where the wavelength of light is λ₀ and n is the absolute refractive index of medium 2, then
λ₂ = λ₀\(\left(\frac{v_{2}}{c}\right)\) = \(\frac{\lambda_{0}}{n}\) (as v₁ = c) …(3)
Now, speed = frequency × wavelength.
Hence, the ratio of the frequencies v₁ and v₂, of the wave in the two mediums can be written using
EQ. (2) as, \(\frac{v_{1}}{v_{2}}\) = \(\frac{v_{1} / \lambda_{1}}{v_{2} / \lambda_{2}}\) = 1 …(4)

Thus, the frequency of a wave remains unchanged while going from one medium to another. Thus, v₀ = v₁ = v₂, where v₀ is the frequency of light in vacuum.

Question 21.
The refractive indices of diamond and water with respect to air are 2.4 and 4/3 respectively. What is the refractive index of diamond with respect to water ?
Answer:

is the refractive index of diamond with respect to water.

Question 22.
What is the refractive index of water with respect to diamond ? For data, see Question 21. above.
Answer:

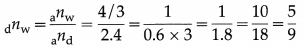
is the refractive index of water with respect to diamond.

Question 23.
What happens to the frequency, wavelength and speed of light as it passes from one medium to another?
Answer:
The wavelength and speed of light change, but the frequency remains the same.

Question 24.
The refractive index of water with respect to air, for light of wavelength Aa in air, is 4/3. What is the wavelength of the light in water?
Answer:

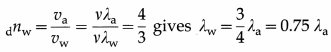
as the wavelength of the light in water.

Question 25.
If the frequency of certain light is 6 × 10¹⁴ Hz, what is its wavelength in free space ? [c = 3 × 10⁸ m/s]
Answer:

is the required wavelength.

Question 26.
If the wavelength of certain light in air is 5000 Å and that in a certain medium is 4000 Å, what is the refractive index of the medium with respect to air ?
Answer:

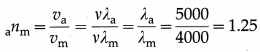
is the refractive index of the medium with respect to air.

Data : c = 3 × 10⁸ m/s

Question 27.
Solve the following :

Question 1.
If the refractive index of glass is 3/2 and that of water is 4/3 respectively, find the speed of light in glass and in water.
Solution:
Let n_g and n_w be the refractive indices of glass and water respectively. Also let v_a, v_g and v_w be the speeds of light in air, glass and water, respectively.

Question 2.
The refractive indices of water and diamond are 4/3 and 2.42 respectively. Find the speed of light in water and diamond.
Solution :

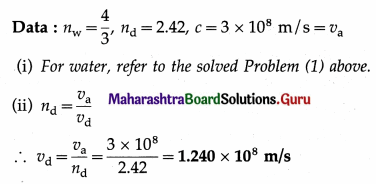
This is the speed of light in diamond.

Question 3.
The refractive indices of glass and water with respect to air are \(\frac{3}{2}\) and \(\frac{4}{3}\), respectively. Determine the refractive index of glass with respect to water.
Solution :


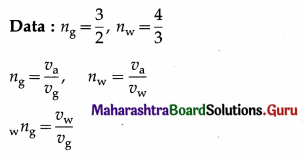
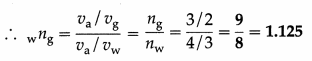
This is the refractive index of glass with respect to water.

Question 4.
A diamond (refractive index = 2.42) is dipped into a liquid of refractive index 1.4. Find the refractive index of diamond with respect to the liquid.
Solution :
Data : n_d = 2.42, n₁ = 1.4
The refractive index of diamond with respect to liquid,

Question 5.
The refractive index of glycerine is 1.46. What is the speed of light in glycerine ? [Speed of light in vacuum = 3 × 10⁸ m/s]
Solution :
Data : n_g = 1.46, c = 3 × 10⁸ m/s c
n_g = \(\frac{c}{v}\)
v = \(\frac{c}{n}\) = \(\frac{3 \times 10^{8}}{1.46}\) = 2.055 × 10⁸ m/s
This is the speed of light in glycerine.

Question 6.
The refractive indices of glycerine and diamond with respect to air are 1.46 and 2.42 respectively. Calculate the speed of light in glycerine and in diamond. From these calculate the refractive index of diamond with respect to glycerine.
Solution:
Let n_g and n_d be the refractive indices of glycerine and diamond respectively. Also, let v_a, v_g and v_d be the speeds of light in air, glycerine and diamond respectively.
Data : v_a = 3 × 10⁸ m/s, n_g = 1.46, n_d = 2.42
(i) Refractive index of glycerine with respect to air,

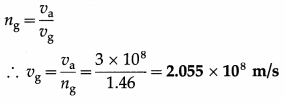
(ii) Refractive index of diamond with respect to air,
n_d = \(\frac{v_{\mathrm{a}}}{v_{\mathrm{d}}}\)

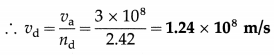
(iii) Refractive index of diamond with respect to glycerine,

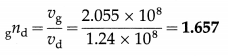
Question 7.
The wavelengths of a certain light in air and in a medium are 4560 Å and 3648 Å, respectively. Compare the speed of light in air with its speed in the medium.
Solution:
Let v_a and v_m be the speeds of light in air and in the medium respectively and let λ_a and λ_m be the wavelengths of light in air and in the medium respectively. Let v be the frequency of light in air.
When light passes from one medium to another, its frequency remains unchanged.

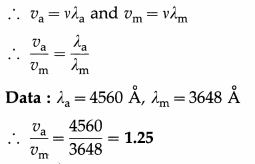
Question 8.
Monochromatic light of wavelength 632.8 nm is incident from air on a water surface. What are the wavelength, frequency and speed of (a) reflected and (b) refracted light ? [Given : Refractive index of water = 1.33]
Solution:
Let v be the frequency of the light, and λ₁ and λ₂ the wavelengths of reflected and refracted light respectively.
Data : λ₁ = 632.8 nm = 632.8 × 10^-9 m,
c = 3 × 10⁸ m/s, _an_w = 1.33
(a) For reflected light:
When the wave travels in air, its speed v₁ = c

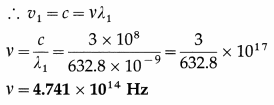
(b) For refracted light:
Frequency does not change while going from one medium to other.
∴ V = 4.741 × 10¹⁴ Hz

This is the speed of the light in water.

Question 9.
The refractive indices of water for red and violet colours are 1.325 and 1.334, respectively. Find the difference between the speeds of the rays of these two colours in water. [c = 3 × 10⁸ m/s]
Solution :
Data : n_r = 1.325, n_v = 1.334, c = 3 × 10⁸ m/s

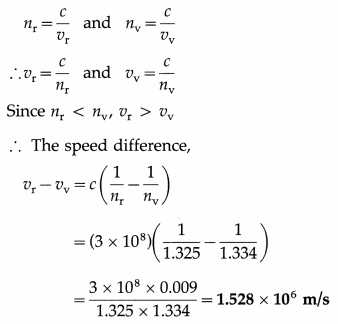
Question 10.
If the difference in speeds of light in glass and water is 2.505 × 10⁷ m/s, find the speed of light in air. [Refractive index of glass = 1.5, refractive index of water = 1.333]
Solution :


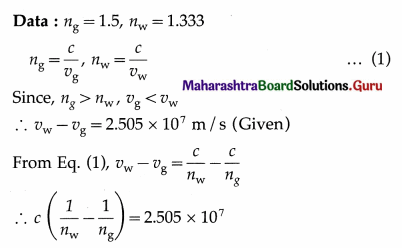
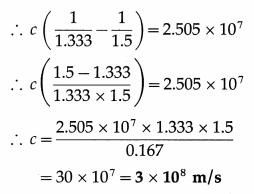
This is the speed of light in air.

Question 11.
If the difference in speeds of light in glass and water is 0.25 × 10⁸ m/s, find the speed of light in air. [n_g = 1.5 and n_w = \(\frac{4}{3}\)]
Solution :

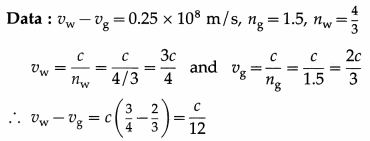
∴ The speed of light in air, c = 12 (n_w – v_g)
= 12 × 0.25 × 10⁸
= 3 × 10⁸ m/s

Question 12.
Red light of wavelength 6400 Å in air has wavelength 4000 Å in glass. If the wavelength of violet light in air is 4400 Å, what is its wavelength in glass? Assume that the glass has the same refractive index for red and violet colours.
Solution :

[ Note : This problem was asked in Board examination in October 2014. The assumption n_r(glass) = n_v(glass) is manifestly gross. No glass can have the same refractive index for red and violet colours.]

Question 13.
A ray of light passes from air to glass. If the angle of incidence is 74° and the angle of refraction is 37°, find the refractive index of the glass.
Solution :
Data : i = 74°, r = 37°
n = \(\frac{\sin i}{\sin r}\) = \(\frac{\sin 74^{\circ}}{\sin 37^{\circ}}\) = \(\frac{0.9613}{0.6018}\)
∴ n = 1.597
This is the refractive index of the glass.

Question 14.
A ray of light is incident on a glass slab making an angle of 30° with the surface. Calculate the angle of refraction in glass and the speed of light in glass. The refractive index of glass and speed of light in air are 1.5 and 3 × 10⁸ m/s, respectively. Solution :
Data : v_air = 3 × 10⁸ m/s; n = 1.5
The angle of incidence (i) is the angle made by the incident ray with the normal drawn to the refracting surface.
∴ i = 90° – 30° = 60°
(a) Angle of refraction (r) in glass :

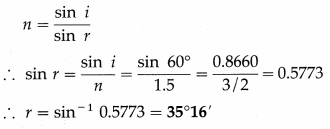
(b) Speed of light (v_glass) in glass :

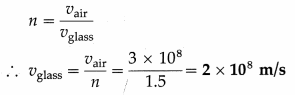
Question 15.
A ray of light is incident on a water surface of refractive index \(\frac{4}{3}\) making an angle of 40° with the surface. Find the angle of refraction.
Solution :

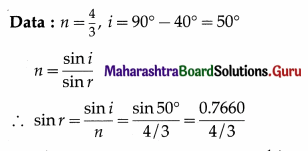
∴ The angle of refraction, r = sin^-1(0.5745) = 35°4′

Question 16.
A ray of light travelling in air is incident on a glass slab making an angle of 30° with the surface. Calculate the angle by which the refracted ray in glass is deviated from its original path and the speed of light in glass [Refractive index of glass = 1.5].
Solution:
Solve for the speed (ug) of light in glass and the angle of refraction (r) in glass as in Solved Problem (14). ug = 2 × 10⁸ m/s and r = 35°16′
The angle of incidence (z), i.e., the angle between the incident ray and the normal to the glass surface, is i = 90° – 30° = 60°.
Hence, the angle by which the refracted ray is deviated from the original path is δ = i – r = 60° – 35°16′ = 24°44′

Question 17.
The wavelength of blue light in air is 4500 A. What is its frequency? If the refractive index of glass for blue light is 1.55, what will be the wavelength of blue light in glass ?
Solution :
Data : λ_a = 4500 Å = 4.5 × 10^-7 m, n_g = 1.55, v_a = 3 × 10⁸ m/s
v_a = v_aλ_a

This is the wavelength of blue light in glass.

Question 18.
White light consists of wavelengths from 400 nm to 700 nm. What will be the wavelength range seen when white light is passed through glass of refractive index 1.55 ?
Solution:
Let λ₁ and λ₂ be the wavelengths of light in water for 400 nm and 700 nm (wavelengths in vacuum) respectively. Let λ_a be the wavelength of light in vacuum.

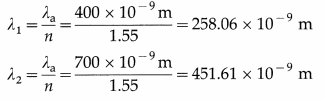
The wavelength range seen when white light is passed through the glass would be 258.06 nm to 451.61 nm.

Question 19.
Determine the change in wavelength of electro-magnetic radiation as it passes from air to glass, if the refractive index of glass with respect to air for the radiation under consideration is 1.5 and the frequency of the radiation is 3.5 × 10¹⁴ Hz. [Speed of the radiation in air (c) = 3 × 10⁸ m/s]
Solution:
Let v be the frequency of the electromagnetic radiation and c its speed in air. Let λ_a and λ_b be the wavelengths of the radiation in air and glass, respectively.

Question 20.
Determine the change in wavelength of light during its passage from air to glass, if the refractive index of glass with respect to air is 1.5 and the frequency of light is 5 × 10¹⁴ Hz. [Speed of light in air = (c) = 3 × 10⁸ m/s] Solution:
Let v be the frequency of the electromagnetic radiation and c its speed in air. Let λ_a and λ_b be the wavelengths of the radiation in air and glass, respectively.

λ_a = 6000 Å, λ_g = 4000 Å ∴ λ_a – λ_g = 2000 Å

Question 21.
A light beam of wavelength 6400 Å is incident normally on the surface of a glass slab of thickness 5 cm. Its wavelength in glass is 4000 A. The beam of light takes the same time to travel from the source to the surface as it takes to travel through the glass slab. Calculate the distance of the source from the surface.
Solution :
Data : λ_a = 6400 Å, s_g = thickness of the glass slab = 5 cm, λ_g = 4000 Å
The speeds of light in glass and air are, respectively, v_g = λ_gv and v_a = λ_av
where the frequency of the light v remains un-changed with the change of medium.
The time taken to travel through the glass slab,
t_g = \(\frac{\mathrm{Sg}}{v_{\mathrm{g}}}\) = \(\frac{S_{g}}{\lambda_{g} v}\)
The time taken to travel through air,
t_a = \(\frac{S_{a}}{v_{a}}\) = \(\frac{d}{\lambda_{\mathrm{a}} v}\)
where s_a = d is the distance of the glass surface from the source.
Since t_a = t_g
\(\frac{d}{\lambda_{\mathrm{a}} v}\) = \(\frac{s_{\mathrm{g}}}{\lambda_{\mathrm{g}} v}\)
∴ d = \(\frac{\lambda_{\mathrm{a}}}{\lambda_{\mathrm{g}}} \mathrm{s}_{\mathrm{g}}\)S_g = \(\frac{6400}{4000}\) × 5 = 1.6 × 5 = 8 cm

Question 22.
A parallel beam of monochromatic light is incident on a glass slab at an angle of incidence 60°. Find the ratio of the width of the beam in glass to that in air if the refractive index of glass is \(\frac{3}{2}\).
Data: i = 60, _an_g = 1.5
By Snell’s law, _an_g = \(\frac{\sin i}{\sin r}\) ∴ sin r = \(\frac{\sin i}{\mathrm{a} n_{\mathrm{g}}}\)
Solution:

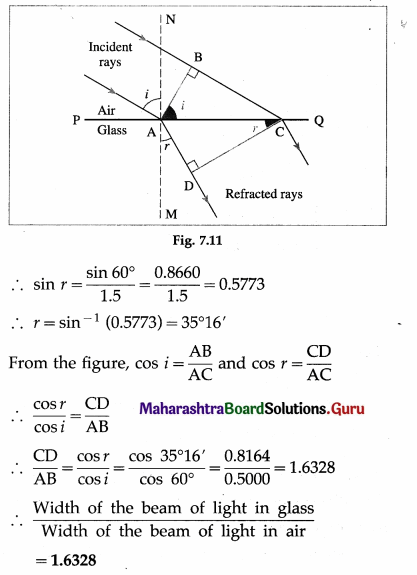
Question 23.
The width of a plane incident wavefront is found to be doubled in a denser medium if it makes an angle of 70° with the surface. Calculate the refractive index for the denser medium.
Solution :

Data : i = 70°, \(\frac{\mathrm{CD}}{\mathrm{AB}}\) = 2
\(\frac{\cos r}{\cos i}\) = \(\frac{\mathrm{CD}}{\mathrm{AB}}\) = 2
∴ cos r = 2 cos 70° = 2 × 0.3420 = 0.6840
∴ r = cos^-10.6840 = 46°51′
The refractive index of the denser medium relative to the rarer medium
= \(\frac{\sin i}{\sin r}\) = \(\frac{\sin 70^{\circ}}{\sin 46^{\circ} 51^{\prime}}\) = \(\frac{0.9397}{0.7296}\) = 1.288

Question 24.
A ray of light travelling through air falls on the surface of a glass slab at an angle i. It is found that the angle between the reflected and the refracted rays is 90°. If the speed of light in glass is 2 × 10⁸ m/s, find the angle of incidence.
Solution :
Data : c = 3 × 10⁸ m/s, v_g = 2 × 10⁸ m/s, angle between the reflected ray and the refracted ray = 90°
n_g = \(\frac{c}{v_{g}}\) = \(\frac{3 \times 10^{8}}{2 \times 10^{8}}\) = 1.5
The angle between the reflected and refracted rays = (90° – i) + (90° – r) = 180° – (i + r) = 90° (by the data)
i + r = 90° ∴ r = 90° – i
∴ sin r = sin(90° – i) = cos i
n_g = \(\frac{\sin i}{\sin r}\) = \(\frac{\sin i}{\cos i}\) = tan i
∴ The angle of incidence,
i = tan^-1 ng = tan^-1 1.5 = 56°19′

Question 28.
What is meant by polarized light ? How does it differ from unpolarized light?
Answer:
According to the electromagnetic theory of light, a light wave consists of electric and magnetic fields vibrating at right angles to each other and to the direction of propagation of the wave. If the vibrations of the electric field \(\vec{E}\) in a light wave are confined to a single plane containing the direction of propagation of the wave so that its electric field is restricted along one particular direction at right angles to the direction of propagation of the wave, the wave is said to be plane-polarized or linearly polarized.

If the vibrations of \(\vec{E}\) in a light wave are in all directions perpendicular to the direction of propagation of the light wave, the light wave is said to be unpolarized. Ordinary light, e.g. that emitted by a bulb, is unpolarized.

According to Biot, unpolarized light may be considered as a superposition of many linearly polarized waves, with random orientations. Also, these component waves are noncoherent, that is, irregular in their phase relationships.

[Note : Ordinary light consists of wave trains, each coming from a separate atom in the source. A beam of ordinary light in a single direction consists of millions of such wave trains from the very large number of atoms in the source radiating in that direction. Hence, the vibrations of \(\vec{E}\) are in all transverse directions with equal probability. Thus, light from an ordinary source is.un-polarized.]

Question 29.
How are polarized light and unpolarized light represented in a ray diagram ?
OR
How will you distinguish between polarized and unpolarized light in a ray diagram?
Answer:
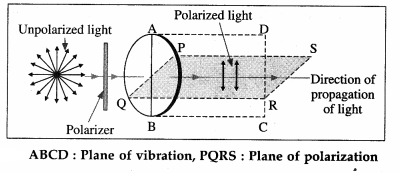
Linearly polarized light is represented in a ray diagram by double-headed arrows or short lines drawn perpendicular to the direction of propagation of light, as shown in below figure.

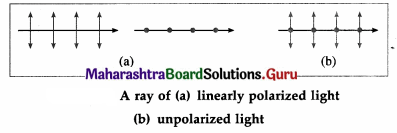
An unpolarized light beam is represented by both dots and arrows, as shown in above figure. The dots are the ‘end views’ of arrows that are oriented normal to the plane of the diagram.

[Note : The length of an arrow or line represents the amplitude of the electric field (\(\vec{E}\)) in the plane of the diagram and the direction indicates the polarization axis of the beam, i.e., the direction of vibration of \(\vec{E}\). According to Jean Biot (1774-1862), French physicist, unpolarized light may be considered as a superposition of many linearly polarized waves, with random orientations in planes perpendicular to the direction of propagation. In an analytical treatment, the electric vectors may be resolved along two mutually perpendicular directions so that the multiplicity of vectors in can be replaced by the two mutually perpendicular vectors as in, both perpendicular to the direction of

propagation of light. Sir David Brewster (1781-1868), British physicist, conceived the ordinary unpolarized light to consist of two perpendicular, polarized components of equal intensity.]

Question 30.
What is a polarizer?
Answer:
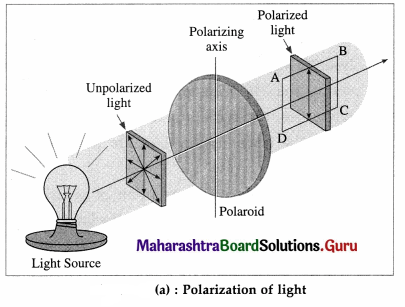
When a beam of unpolarized light is passed through certain types of materials (or devices), these materials (or devices) allow only those light waves to pass through which have their electric field along a particular direction. All the other waves with the electric field in other directions are blocked. A material (or a device) which exhibits this special property is called a polarizer.

Question 31.
Explain the terms :

1. polarizing axis of a polarizer
2. plane of vibration
3. plane of polarization.

Answer:

1. Polarizing axis of a polarizer : When unpolarized light is incident on a polarizer, the particular direction along which the electric field of the emergent wave is oriented is called the polarizing axis of the polarizer.
2. Plane of vibration : The plane of vibration of an electromagnetic wave is the plane of vibration of the electric field vector containing the direction of propagation of the wave. Experiment shows that it is the electric field vector E which produces the optical polarization effects.
3. Plane of polarization : The plane of polarization of an electromagnetic wave is defined as the plane perpendicular to the plane of vibration. It is the plane containing the magnetic field vector and the direction of propagation of the wave.
   

Note :
For vision, photography, action of light on electrons and many other observed effects of light, it is the electric vector that is more important than the magnetic one. Hence, nowadays the plane of polarization is taken to be the plane of vibration. Most authoritative; modern books on Optics do not, therefore, explicitly define the plane of vibration. The above convention is obsolete and redundant.

Question 32.
What is a Polaroid? Explain its construction.
Answer:
A Polaroid is a synthetic dichroic sheet polarizer packed with tiny dichroic crystals oriented parallel to each other such that the transmitted light is plane polarized.

Construction : The first large polarizing sheet filter was made by US inventor Edwin H. Land (1909-91). He used the microscopic needlelike crystals of iodoquinine sulphate (known as herapathite) made into a thick colloidal dispersion in nitrocellulose. This material was squeezed through a long narrow slit which forced the needles to orient parallel to one another. The material was then dried to form a solid plastic sheet.

[Note : The modern version of Polaroid is made from long-chain polymer, polyvinyl alcohol. The transmission axis of a Polaroid is the plane of vibration of a plane polarized light which passes through with minimum absorption.]

If the vibrations of the electric field \(\vec{E}\) in a light wave are confined to a single plane containing the direction of propagation of the wave so that its electric field is restricted along one particular direction at right angles to the direction of propagation of the wave, the wave is said to be plane-polarized or linearly polarized.

This phenomenon of restricting the vibrations of light, i.e., of the electric field vector in a particular direction, which is perpendicular to the direction of the propagation of the wave is called polarization of light.

Consider an unpolarized light wave travelling along the x-direction. Let c, v and λ be the speed, frequency and wavelength, respectively, of the wave. The magnitude of its electric field (\(\vec{E}\)) is,
E = E₀ sin (kx – ωt), where E₀ = E_max = amplitude of the wave, ω = 2πv = angular frequency of the wave and k = \(\frac{2 \pi}{\lambda}\) = magnitude of the wave vector or propagation vector.
The intensity of the wave is proportional to |E₀|². The direction of the electric field can be anywhere in the y-z plane. This wave is passed through two identical polarizers as shown.

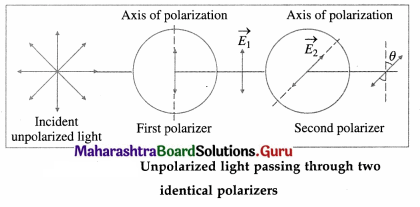
When a wave with its electric field inclined at an angle φ to the axis of the first polarizer is passed through the polarizer, the component E₀ cos φ will pass through it. The other component E₀ sin φ which is perpendicular to it will be blocked.

Now, after passing through this polarizer, the intensity of this wave will be proportional to the square of its amplitude, i.e., proportional to |E₀ cos φ|².

The intensity of the plane-polarized wave emerging from the first polarizer can be obtained by averaging E₀ cos φ|² over all values of φ between 0 and 180°. The intensity of the wave will be
proportional to \(\frac{1}{2}\) |E₀|² as the average value of cos² φ over this range is \(\frac{1}{2}\). Thus the intensity of an unpolarized wave reduces by half after passing through a polarizer.

When the plane-polarized wave emerges from the first polarizer, let us assume that its electric field (\(\overrightarrow{E_{1}}\)) is along the y-direction. Thus, this electric field is,
\(\overrightarrow{E_{1}}\) = \(\hat{i}\)E₁₀ sin (kx – ωt) … (1)
where, E₁₀ is the amplitude of this polarized wave. The intensity of the polarized wave,
I₁ ∝|E₁₀|² …(2)

Now this wave passes through the second polarizer whose polarization axis (transmission axis) makes an angle θ with the y-direction. This allows only the component E₁₀ cos θ to pass through it. Thus, the amplitude of the wave which passes through the second polarizer is E₂₀ = E₁₀ cos θ and its intensity,
I₂ ∝|E₂₀|²
∴ I₂ ∝ | E₁₀|² cos² θ
∴ I₂ = I₁ cos² θ … (3)

Thus, when plane-polarized light of intensity I₁ is incident on the second identical polarizer, the intensity of light transmitted by the second polarizer varies as cos² θ, i.e., I₂ = I₁ cos² θ, where θ is the angle between the transmission axes of the two polarizers. This is known as Malus’ law.

[Note : Etienne Louis Malus (1775-1812), French military engineer and physicist, discovered in 1809 that light can be polarized by reflection. He was the first to use the word polarization, but his arguments were based on Newton’s corpuscular theory.]

Question 33.
Unpolarized light is passed through two polarizers. Under what condition is the intensity of the emergent light
(i) maximum
(ii) zero?
Answer:
If the angle θ between the axes of polarization of the two polarizers, is 0°, i.e., the polarization axes of the two polarizers are parallel, the intensity of emergent light is maximum. If θ = 90°, i.e., the polarization axes of the two polarizers are perpendicular, no light emerges from the second polarizer, thus the intensity of emergent light is minimum.
[Note: θ = 0° and 90° are known as parallel and cross settings of the two polarizers.]

Question 34.
With a neat labelled diagram, explain the use of a pair of polarizers to vary the intensity of light. What are crossed polarizers?
Answer:
Consider an unpolarized light beam incident perpendicularly on the first polarizing sheet, called the polarizer, whose transmission axis is vertical, say. The light emerging from this sheet is polarized vertically, and the transmitted electric field is \(\overrightarrow{E_{0}}\).

The polarized light beam then passes through a second polarizing sheet, called the analyser, which is placed parallel to the polarizer with its transmission axis at an angle θ to the transmission axis of the polarizer. The component of \(\overrightarrow{E_{0}}\) which is perpendicular to the axis of the analyser is completely absorbed, and the component parallel to that axis is E₀ cos θ.

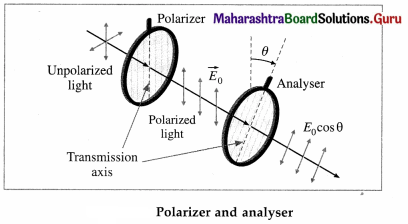
Since intensity varies as the square of the amplitude, the transmitted intensity varies as I = I₀ cos² θ

where I₀ is the incident light intensity on the analyser. This expression (known as Malus’s law) shows that the transmitted intensity is maximum when the transmission axes are parallel and zero when the transmission axes are perpendicular to each other.

Crossed polarizers are a pair of polarizers with their transmission axes perpendicular to each other so that the transmitted light intensity is zero.

Question 35.
If the angle made by the axis of polarization of the second polarizer to that of the first polarizer is 60°, what can you say about the intensity of the light transmitted by the second polarizer?
Answer:
If I₁ is the intensity of the light incident on the second polarizer and I₂ is the intensity of the light transmitted by the second polarizer,
I₂ = I₁ cos² θ = I₁ cos² 60°
= I₁\(\left(\frac{1}{2}\right)^{2}\)
= \(\frac{\boldsymbol{I}_{1}}{4}\)

Question 36.
If 75% of incident light is transmitted by the second polarizer, what is the angle made by the transmission axis of the second polarizer to the transmission axis of the first polarizer?
Answer:

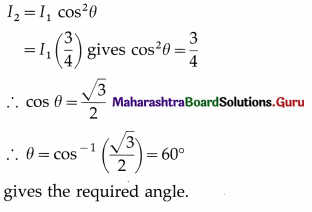
Question 37.
Explain the phenomenon of polarization of light by reflection.
Answer:
Consider a ray of unpolarized monochromatic light incident at an angle θ_B on a boundary between two transparent media as shown. Medium 1 is a rarer medium with refractive index n₁ and medium 2 is a denser medium with refractive index n₂. Part of incident light gets refracted and the rest

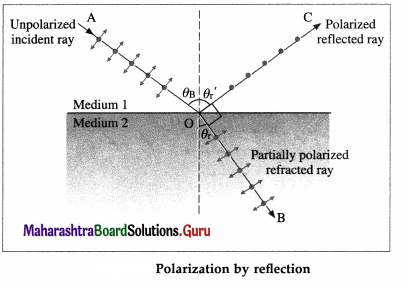
gets reflected. The degree of polarization of the reflected ray varies with the angle of incidence.

The electric field of the incident wave is in the plane perpendicular to the direction of propagation of incident light. This electric field can be resolved into a component parallel to the plane of the paper, shown by double arrows, and a component perpendicular to the plane of the paper shown by dots, both having equal magnitude. Generally, the reflected and refracted rays are partially polarized, i.e., the two components do not have equal magnitude.

In 1812, Sir David Brewster discovered that for a particular angle of incidence. θ_B, the reflected wave is completely plane-polarized with its electric field perpendicular to the plane of the paper while the refracted wave is partially polarized. This particular angle of incidence (θ_B) is called the Brewster angle.

For this angle of incidence, the refracted and reflected rays are perpendicular to each other. For angle of refraction θ_r,
θ_B + θ_r = 90° …… (1)
From Snell’s law of refraction,
∴ n₁ sin θ_B = n₂ sin θ_r … (2)
From Eqs. (1) and (2), we have,

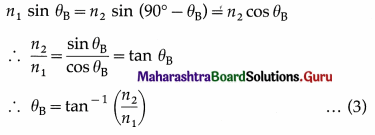
This is called Brewster’s law.

Question 38.
Define polarizing angle. At the polarizing angle, what is the plane of polarization of the reflected ray ?
Answer:
Polarizing angle : The polarizing angle for an interface is the angle of incidence for a ray of unpolarized light at which the reflected ray is completely polarized.

At the polarizing angle, the reflected ray is completely plane polarized in the plane of incidence.

Question 39.
Give one example in which polarization by reflection is used.
Answer:
Polarization by reflection is used to cut out glare from nonmetallic surfaces. Special sunglasses are used for this purpose. Sunglasses fitted with Polaroids reduce the intensity of partially or completely polarized / reflected light incident on the eyes from reflecting surfaces.

Question 40.
State any four uses of a Polaroid.
Answer:

1. A Polaroid lens filter makes use of polarization by reflection. This filter is used in photography to reduce or eliminate glare from reflective nonmetallic surfaces like glass, rock faces, water and foliage. It can also deepen the colour of the skies.
2. Polaroid sunglasses reduce the transmitted intensity by a factor of one half and also reduce or eliminate glare from nonmetallic surfaces such as asphalt roadways and snow fields.
3. Polaroid filters are used in liquid crystal display (LCD) screens.
4. Polaroids are used to produce and show 3-D movies to give the viewer a perception of depth.

[Note :Three-dimensional movies are filmed from two slightly different camera locations and shown at the same time through two projectors fitted with polarizers having different transmission axes. The audience wear glasses which have two Polaroid filters whose transmission axes are the same as those on the projectors.]

Question 41.
Explain the phenomenon of polarization by scattering.
Answer:
When a beam of sunlight strikes air molecules or dust particles whose size is of the order of wavelength of light, the beam gets scattered. The scattered light observed in a direction perpendicular to the direction of incidence, is plane polarized. This phenomenon is called polarization by scattering.

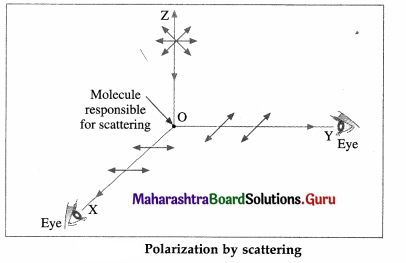
As shown in above figure, a beam of an un-polarized light is incident along the Z-axis on a molecule. Light waves being transverse in nature, all the possible directions of vibration of electric field vector in the unpolarized light are confined to the XY plane. The light incident on the molecule is scattered by the electromagnetic field of the molecule.

When observed along the X-axis, only the vibrations of electric field vector which are parallel to Y-axis can be seen. In the similar manner, when observed along the Y-axis, only the vibrations of electric field vector which are parallel to the X-axis can be seen. Thus, the light scattered in a direction perpendicular to the incident light is plane polarized.

Question 42.
Solve the following.

Question 1.
The angle between the transmission axes of two polarizers is 45°. What will be the ratio of the intensities of the original light and the transmitted light after passing through the second polarizer?
Solution :
Data : θ = 45°
According to Malus’ law,
I₂ = I₂ cos² θ

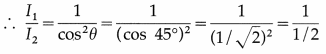
= 2
This is the required ratio.

Question 2.
Two polarizers are so oriented that the maximum amount of light is transmitted. To what fraction of its maximum value is the intensity of the transmitted light reduced when the second polarizer is rotated through
(a) 300
(b) 600?
Solution:
Data : θ = 30°, 60°,
I₂ = I₂ cos²θ
where I₁ is the intensity of the incident light and I₂ is that of the transmitted light.
(i) For θ = 30°

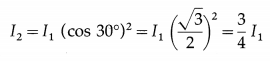
I₂ = 0.75 I₁
= 75% of I₁

(ii) For θ = 60°
I₂ = I₁ (cos 60°)²
= I₁\(\left(\frac{1}{2}\right)^{2}\) = \(\frac{1}{4}\)I₁
= 0.25 I₁ = 25% of I₁

Question 3.
For a glass plate as a polarizer with refractive index 1.633, calculate the angle of incidence at which reflected light is completely polarized.
Solution :
Data : n = 1.633
tan θ_B = n = 1.633
∴ The polarizing angle,
θ_B = tan^-1 1.633 = 58°31′

Question 4.
Find the refractive index of glass if the angle of incidence at which the light reflected from the surface of the glass is completely polarized is 58°.
Solution :
Data : θ_B = 58°
n_g = tan θ_B = tan 58° .
= 1.6003
This is the refractive index of the glass.

Question 5.
The critical angle for a glass-air interface is sin^-1\(\frac{5}{8}\). A ray of unpolarized monochromatic light in air is incident on the glass. What is the polarizing angle?
Solution :
Data : θ_c = sin^-1 \(\frac{5}{8}\)
∴ sin θ_c = \(\frac{5}{8}\)
∴ n = \(\frac{1}{\sin \theta_{\mathrm{c}}}\) = \(\frac{8}{5}\) = 1.6
Also, n = tan θ_B
∴ θ_B = tan^-1 n
∴ The polarizing angle, θ_B = tan^-1 1.6 = 58°

Question 6.
The refractive index of a medium is \(\sqrt{3}\). What is the angle of refraction, if the unpolarized light is incident on it at the polarizing angle of the medium?
Solution :

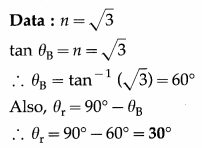
This is the angle of refraction.

Question 7.
For a given medium, the polarizing angle is 60°. What is the critical angle for this medium ?
Solution :

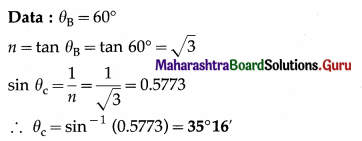
This is the critical angle for the medium.

Question 8.
Unpolarized light is incident on a plane glass surface. What should be the angle of incidence so that the reflected and refracted rays are perpendicular to each other? [Given n = 1.5]
Solution :
Data : Refractive index, n = 1.5
The reflected and refracted rays will be perpendicular to each other, when the angle of incidence = the polarizing angle θ_B,
tan θ_B = n = 1.5
∴ θ_B = tan^-1 (1.5) = 56°19′

Question 9.
If a glass plate of refractive index 1.732 is to be used as a polarizer, what would be the
(i) polarizing angle and
(ii) angle of refraction?
Solution :
Data : n_g = 1.732
n_g = tan θ_B
0B = tan^-1 (1.732) = 60°
This is the polarizing angle,

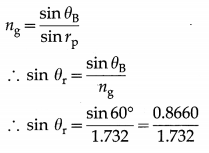
∴ θ_r = sin^-1\(\left(\frac{0.8660}{1.732}\right)\)
= sin^-1 (0.5) = 30°
This is the angle of refraction.

Question 10.
For a certain unpolarized monochromatic light incident on glass and water, the polarizing angles are 59°32′ and 53°4′, respectively. What would be the polarizing angle for the light if it is incident from water on to the glass?
Solution:

Question 11.
The wavelengths of a certain blue light in air and in water are 4800 Å and 3600 Å, respectively. Find the corresponding Brewster angle.
Solution:

This is the Brewster angle for the given light incident on water surface.

Question 12.
A ray of light is incident on a glass slab at the polarizing angle of 58°. Calculate the change in the wavelength of light in glass.
Solution :


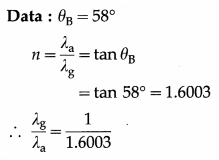
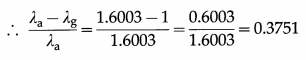
∴ The change in the wavelength of the light in glass, λ_a – λ_b = 0.37514λ_a, i.e., 37.51% of its wavelength in air.

Question 13.
For what angle of incidence will light incident on a bucket filled with liquid having refractive index 1.3 be completely polarized after reflection ?
Solution:
The reflected light will be completely polarized when the angle of incidence is equal to the Brewster’s angle which is given by θ_B = tan^-1 \(\frac{n_{2}}{n_{1}}\), where n₁ and n₂ are refractive indices of the first and the second medium respectively. In this case, n₁ = 1 and n₂ = 1.3.
Thus, the required angle of incidence = Brewster’s angle = tan^-1\(\frac{1.3}{1}\) = 52.26°

Question 43.
State and explain the principle of superposition of waves.
Answer:
Principle of superposition of waves : The dis-placement at a point due to the combined effect of a number of waves arriving simultaneously at the point is the vector sum of the displacements due to the individual waves arriving at the point.

Explanation : This is a general principle of linear systems applied to wave phenomena. When two or more wave trains arrive at a point simultaneously, they interpenetrate without disturbing each other. The resultant displacement at that point is the vector sum of the displacements due to the individual waves arriving at the point. The amplitude and phase angle of the resulting disturbance are functions of the individual amplitudes and phases.

Notes :

1. In the case of mechanical waves, e.g., sound, the displacement is that of a vibrating particle of the medium.
2. When we consider superposition of electromagnetic waves, light in this chapter, the term displacement refers to the electric field component of the electromagnetic wave.

Question 44.
Explain what you understand by interference of light.
Answer:
The phenomenon in which the superposition of two or more light waves produces a resultant disturbance of redistributed light intensity or energy is called the interference of light.

Light waves are transverse in nature. If two monochromatic light waves of the same frequency arrive in phase at a point, the crest of one wave coincides with the crest of the other and the trough of one wave coincides with the trough of the other. Therefore, the resultant amplitude and hence the resultant intensity of light at that point is maximum and the point is bright. This phenomenon is called constructive interference. If two light waves having the same amplitude are in opposite phase, the crest of one wave coincides with the trough of the other. Therefore, the resultant amplitude, and hence the intensity, at that point is minimum (zero) and the point is dark. This phenomenon is called destructive interference. If the amplitudes are unequal, the resultant amplitude is minimum, but not zero. At other points, the intensity of light lies between the maximum and zero.

Question 45.
Explain how the phenomenon of interference can be demonstrated in a ripple tank.
Answer:

1. ‘Two pins, a small distance d apart, are attached to the electrical vibrator or an electrically maintained tuning fork of a ripple tank. The pins are kept vertical with their tips in contact with the surface of water in the ripple tank.
2. When the vibrator is switched on, the two pins vibrate together in phase with the same frequency and the same amplitude. Their tips form the sources S₁ and S₂ of circular waves which spread outward along the water surface.
   
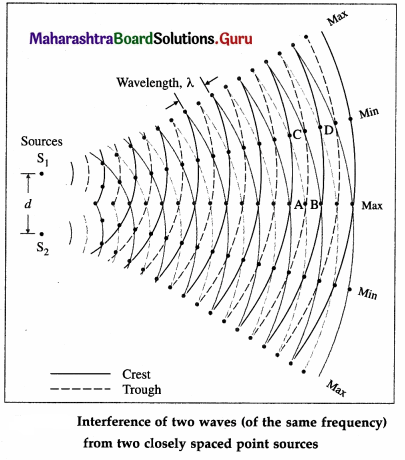
3. The waves from the two sources interfere constructively at points where they meet in phase. Thus, where the crest of a wave from S₁ is superposed on the crest of a wave from S₂ (such as point A), and where the trough of a wave from S₁ is superposed on the trough of a wave from S₂ (such as point B), the water molecules have maximum amplitude of vibration.
4. The waves from the two sources interfere destructively at points where they meet in opposite phase. Thus, where the crest of a wave from S₁ is superposed on the trough of a wave from S₂ (such as point C), and where the trough of a wave from S₁ is superposed on the crest of a wave from S₂ (such as point D), the water molecules have minimum amplitude of vibration.

Question 46.
What are coherent sources? Is it possible to observe interference pattern with light from any two different sources ? Why ?
Answer:
Coherent sources : Two sources of light are said to be coherent if the phase difference between the emitted waves remains constant.

It is not possible to observe interference pattern with light from any two different sources. This is because, no observable interference phenomenon occurs by superposing light from two different sources. This happens due to the fact that different sources emit waves of different frequencies. Even if the two sources emit light of the same frequency, the phase difference between the wave trains from them fluctuates randomly and rapidly, i.e., they are not coherent.

Consequently, the interference pattern will change randomly and rapidly, and steady interference pattern would not be observed.

Question 47.
State the conditions for constructive and destructive interference of light.
Answer:
(1) Constructive interference (brightness) : There is constructive interference at a point and the brightness or intensity is maximum there, if the two waves of light of the same frequency arrive at the point in phase, i.e., with a phase difference of zero or an integral multiple of 2π radians.
A phase difference of 2π radians corresponds to a path difference λ, where λ is the wavelength of light. Since

for constructive interference with maximum intensity of light, phase difference = 0, 2π, 4π, 6π, … rad
= n(2π) rad
or path difference = 0, λ, 2λ, 3λ, …, etc.
= nλ
where n = 0, 1, 2, 3, …, etc.

(2) Destructive interference (darkness) : There is destructive interference at a point and the point is the darkest, i.e., the intensity of light is minimum, if the two waves of light of the same frequency and intensity arrive at the point in opposite phase, i.e., with a phase difference of an odd-integral multiple of π radians. A phase difference 2π radians corresponds to a path difference λ, where λ is the wavelength of light.
∴ For destructive interference with minimum intensity of light, phase difference = π, 3π, 5π, … rad
= (2m – 1)π rad
or path difference = λ/2, 3λ/2, 5λ/2, …, etc.
= (2m – 1)\(\frac{\lambda}{2}\)
where m = 1, 2, 3, …, etc.

Question 48.
In Young’s double-slit experiment using light of wavelength 5000Å, what phase difference corresponds to the 11th dark fringe from the centre of the interference pattern?
Answer:
The required phase difference is (2m – 1)π rad = (2 × 11 – 1)π rad = 21π rad.

Question 49.
In Young’s double-slit experiment, if the path difference at a certain point on the screen is 2.999 λ, what can you say about the intensity of light at that point ?
Answer:
The intensity of light at that point will be close to the maximum intensity and the point will be nearly bright as the path difference = 2.999 λ \(\approx\) 3λ (integral multiple of λ).

Question 50.
In Young’s double-slit experiment, if the path difference at a certain point on the screen is 7.4999 λ, what can you say about the nature of the illumination at that point ?
Answer:
The point will be nearly dark as the path difference = 7.4999 λ \(\approx\) (8 – 0.5) λ, which is of the form
(m – \(\frac{1}{2}\))λ, where m = 1, 2, … …. 8

Question 51.
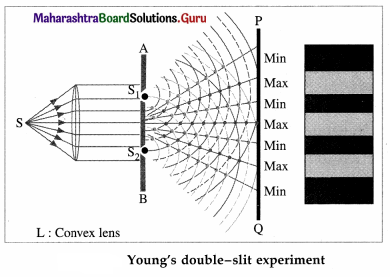
How is Young’s interference experiment performed using a single source of light?
Answer:
When a narrow slit is placed in front of an intense source of monochromatic light, cylindrical wave-fronts propagate from the slit. In Young’s experiment, two coherent sources are then obtained by wavefront splitting by placing a second screen with two narrow slits at a small distance from the first slit.

Question 52.
State any two points of importance of Young’s experiment to observe the interference of light.
Answer:
Importance of Young’s experiment observe the interference of light:

1. It was the first experiment (1800-04) in which the interference of light was observed.
2. This experiment showed that light is propagated in the form of waves.
3. From this experiment, the wavelength of monochromatic light can be determined.

Question 53.
What is the nature of the interference pattern obtained using white light?
Answer:
With white light, one gets a white central fringe at the point of zero path difference along with a few coloured fringes on both the sides, the colours soon fade off to white.

The central fringe is white because waves of all wavelengths constructively interfere here. For a path difference of \(\frac{1}{2}\)λ_violet, complete destructive interference occurs only for the violet colour; for waves of other wavelengths, there is only partial destructive interference. Consequently, we have a line devoid of violet colour and thus reddish in appearance. A point for which the path difference = \(\frac{1}{2}\)λ_red is similarly devoid of red colour, and appears violettish. Thus, following the white central fringe we have coloured fringes, from reddish to violettish. Beyond this, the fringes disappear because there are so many wavelengths in the visible region which constructively interfere that we observe practically uniform white illumination.

Question 54.
In Young’s double-slit experiment, the second minimum in the interference pattern is exactly in front of one slit. The distance between the two slits is d and that between the source and screen is D. What is the wavelength of the light used ?
Answer:
The distance of the mth minimum from the central fringe is,

This is the wavelength of the light used.

Question 55.
In Young’s double-slit experiment, a glass slide of refractive index n_g and thickness b is placed in front of one of the slits. What happens to the interference pattern and fringe width ? Derive an expression for the positions of the bright fringes in the interference pattern.
Answer:
Suppose, in Young’s double-slit experiment, a glass slide of refractive index n_g and thickness b is placed in front of the slit S₁.

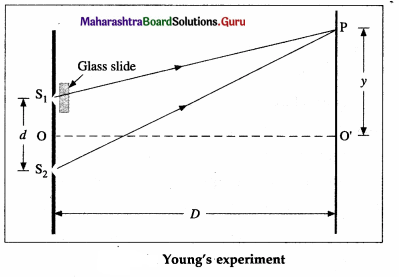
If the experiment is set up in free space, this introduces an additional optical path length (n_g – 1)b in the path S₁P.
Then, the optical path difference to the point P from S₁ and S₂ is,
∆l = S₂P – [S₁P + (n_g – 1)b] = (S₂P – S₁P) – (n_g – 1)b = y\(\frac{d}{D}\) – (n_g – 1)b … (1)
where y = PO’, d is the distance between S₁ and S₂, and D is the distance of the screen from S₁ and S₂. Thus, point P will be bright (maximum intensity) if ∆l = nλ, where n = 0, 1, 2, … . The central bright fringe, corresponding to n = 0, will be obtained at a distance y₀ from O’ such that,
∆l = y_o\(\frac{d}{D}\) – (n_g – 1)b = 0
∴ y_o\(\frac{d}{D}\) = (n_g – 1)b ∴ y₀ = \(\frac{D}{d}\)(ng-l) b …(2)
Therefore, the central bright fringe and the interference pattern will shift up (towards P) by a distance y₀ given by EQ. (2).
The distance of the nth bright fringe from O’ towards P is,

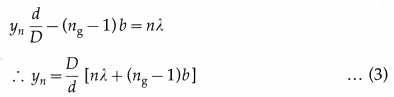
The distance of the (n + l)th bright fringe from O’ towards P is

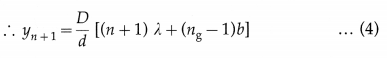
Therefore, the fringe width,
w = y_n+1 – y_n = \(\frac{\lambda D}{d}\) ….(5)
Thus, the fringe width remains unchanged.

Question 56.
What happens to the interference pattern when the phase difference between the two sources of light changes with time ?
Answer:
If the two sources do not maintain their phase relation during the time required for observation, the intensity of light at any point on the screen and consequently the interference pattern changes rapidly, and hence steady interference pattern is not observed.

Question 57.
Obtain expressions in terms of electric field, for the resultant amplitude and the intensity for the interference pattern produced by monochromatic light waves from two coherent sources.
Answer:
Consider a two-source interference pattern produced by superposition of monochromatic light waves of angular frequency ω, wavelength λ and constant phase difference, φ. At the centre of a bright fringe, there is constructive interference. Here, the amplitude of the resultant wave is double the amplitude of the wave incident on AB. Now, the intensity is proportional to the square of the amplitude of the wave. Hence, the resultant intensity is, I = 4I₀, where I₀ is the intensity of the incident wave. At the centre of a dark fringe, there is destructive interference. Here, the amplitude of the resultant wave and hence the intensity is zero. At other points the intensity is between 4I₀ and zero, depending on the phase difference.

Let the equations of the two waves coming from S₁ and S₂ at some point in the interference pattern be, E₁ = E₂ sin ωt and E₂ = E₀ sin (ωt + φ) respectively, where E₀ is the amplitude of the electric field vector.

By the principle of superposition of waves, the resultant electric field at that point is the algebraic sum, E = E₁ + E₂
∴ E = E₀ sin ωt + E₀ sin (ωt + φ)
= E₀ [sin ωt + sin (ωt + φ)]
= 2E₀ sin (ωt + φ/ 2) cos (φ/2)
The amplitude of the resultant wave is 2 E₀ cos (φ/2).
Therefore, the intensity at that point is I ∝ |2 E₀ cos (φ/2) |²
∴ I = 4I₀ cos² (φ/2)
as I₀ ∝ |E₀|².

Question 58.
Monochromatic light waves of amplitudes E₁₀ and E₂₀ and a constant phase difference φ produce an interference pattern. State an expression for the resultant amplitude at a point in the pattern. Hence, deduce the conditions for
(i) constructive interference with maximum intensity
(ii) destructive interference with minimum intensity. Also show that the ratio of the maximum and minimum intensities is
\(\frac{I_{\max }}{I_{\min }}\) = \(\left(\frac{\boldsymbol{E}_{10}+\boldsymbol{E}_{20}}{\boldsymbol{E}_{10}-\boldsymbol{E}_{20}}\right)^{2}\)
Answer:
Consider a two-source interference pattern produced by monochromatic light waves of angular frequency ω, wavelength λ, amplitudes E₁₀ and E₂₀ and a constant phase difference φ.

Let the individual electric fields along the same line due to the waves at some point in the interference pattern be
E₁ = E₁₀ sin ωt and E₂ = E₂₀ sin (ωt + φ)
By the principle of superposition of waves, the resultant electric field (displacement) at that point is the algebraic sum

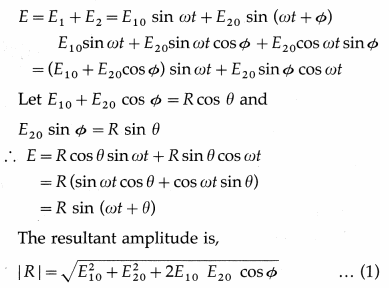
Since, the intensity of a wave is proportional to the square of its amplitude, the resultant intensity at P,
I ∝ |R|²

Thus, the intensity depends on cos φ.
The condition for constructive interference with maximum intensity is cos φ is maximum, equal to 1, i.e., φ = 2nπ (n = 0, 1, 2, 3…) … (3)
The condition for destructive interference with minimum intensity is cos φ is minimum equal to

Question 59.
If the amplitude ratio (E₂₀/E₁₀) of two interfering coherent waves producing an interference pattern is 0.5, what is the ratio of the minimum intensity to maximum intensity?
Answer:

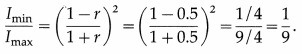
Question 60.
If the amplitude ratio (E₂₀/E₁₀) of two interfering coherent waves producing an interference pattern is 0.8, what is the ratio of the maximum intensity to the minimum intensity?
Answer:

Question 61.
Two slits in Young’s experiment have widths in the ratio 2 : 3. What is the ratio of the intensities of light waves coming from them?
Answer:
The required ratio is \(\frac{I_{1}}{I_{2}}\) = \(\frac{w_{1}}{w_{2}}\) = \(\frac{2}{3}\)

Question 62.
Monochromatic light waves of intensities I₁ and I₂, and a constant phase difference φ produce an interference pattern. State an expression for the resultant intensity at a point in the pattern. Hence deduce the expressions for the resultant intensity, maximum intensity and minimum intensity if I₁ = I₂ = I₀.
Answer:
Consider a two-source interference pattern produced by monochromatic light waves of intensities I₁ and I₂, and a constant phase difference φ. The resultant intensity at a point in the pattern is

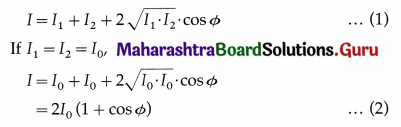
At a point of constructive interference with maximum intensity, cos φ = 1.
∴ I_max = 2I₀(1 + 1) = 4I₀ …(3)
At point of destructive interference, with minimum intensity, cos φ = – 1.
∴ I_min = 2I₀(1 – 1) = 0… (4)
Notes :

(1) Since 1 + cos φ = 2 cos²φ, EQ. (2) above can be expressed as I = 4I₀ cos²\(\frac{\phi}{2}\) = I_max cos²\(\frac{\phi}{2}\).

(2) The average of cos² \(\frac{\phi}{2}\), averaged over one cycle, is \(\frac{1}{2}\).
Therefore, the average intensity of a bright and dark fringe in an interference pattern is I_av = 4I₀ × \(\frac{1}{2}\) = 2I₀. The graph of l versus φ is shown, in which the dotted line shows I_av.

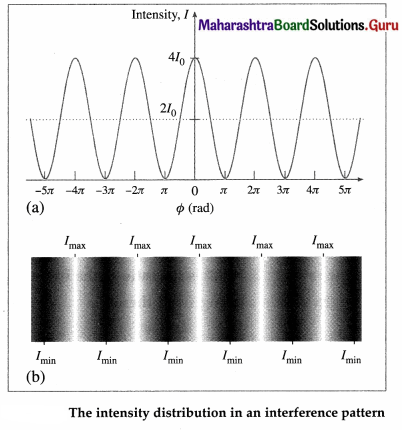
In the absence of interference phenomenon, the intensity at a point due to two waves each of intensity I₀ is 2I₀, which is the same as the average intensity in an interference pattern. Thus, interference of light is consistent with the law of conservation of energy. Interference produces a redistribution of energy out of regions where it is destructive into the regions where it is constructive.

Question 63.
At a point in an interference pattern, the two interfering coherent waves of equal intensity I₀ have phase difference 60°. What will be the resultant intensity at that point ?
Answer:
Resultant intensity, I₀ = 2I₀ (1 + cos φ)
= 2I₀(1 + cos 60°) = 2I₀(1 + \(\frac{1}{2}\)) = 3I₀.

Question 64.
Solve the following :

Question 1.
Find the ratio of intensities at two points X and Y on a screen in Young’s double-slit experiment where waves from the slits S₁, and S₂ have path difference of 0 and \(\frac{\lambda}{4}\) respectively.
Solution :

Question 2.
Two coherent sources, whose intensity ratio is 81 : 1, produce interference fringes. Calculate the ratio of the intensities of maxima and minima in the fringe system.
Solution :
Data : I₁ : I₂ = 81 : 1
If E₁₀ and E₂₀ are the amplitudes of the interfering waves, the ratio of the maximum intensity to the minimum intensity in the fringe system is

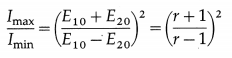
Question 3.
In Young’s double-slit experiment, the ratio of the intensities at the maxima and minima in the interference pattern is 36 : 16. What is the ratio of the widths of the two slits?
Answer:

Question 4.
In Young’s double-slit experiment, the ratio of the intensities of the maxima and minima in an interference pattern is 36 : 9. What is the ratio of the intensities of the two interfering waves?
Answer:

∴ The ratio of the intensities of the two interfering waves is 9 : 1.

Question 5.
Two slits in Young’s double-slit experiment have widths in the ratio 81 : 1. What is the ratio of the amplitudes of light waves coming from them?
Solution:
Data : w₁ : w₂ = 81 : 1
Since the intensity of a wave is directly proportional to the square of its amplitude,
\(\frac{I_{1}}{I_{2}}\) = \(\left(\frac{E_{10}}{E_{20}}\right)\) …. (1)
Also, the intensity of a wave coming out of a slit is directly propotional to the slit width.
∴ \(\frac{I_{1}}{I_{2}}\) = \(\frac{w_{1}}{w_{2}}\) …. (2)
From Eqs. (1) and (2),

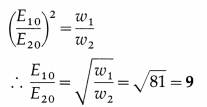
The ratio of the amplitudes of light waves from the slits is 9: 1.

Question 6.
Two monochromatic light waves of equal intensities produce an interference pattern. At a point in the pattern, the phase difference between the interfering waves is π/3 rad. Express the intensity at this point as a fraction of the maximum intensity in the pattern.
Solution :
Data : I₁ = I₂ = I₀, φ = π/3 rad
The resultant intensity at the point in the pattern is

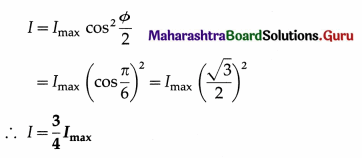
Question 7.
In Young’s double-slit experiment using monochromatic light of wavelength λ, the intensity of light at a point on the screen where the path difference is λ is I. What is the intensity of light at a point where the path difference is λ/3 ?
Solution :
Data : ∆l₁ = λ, I₁ = I, ∆l₂ = λ/3
We assume that light waves coming out of the two slits are of equal intensity I₀.
Then, at a point in the interference pattern where the phase difference between the interfering waves is φ, the resultant intensity is,
I = 2I₀ (1 + cos φ)
Phase difference (φ) = \(\frac{2 \pi}{\lambda}\) × path difference (∆l)


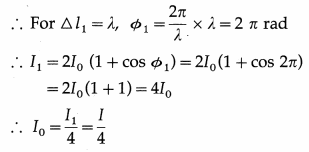
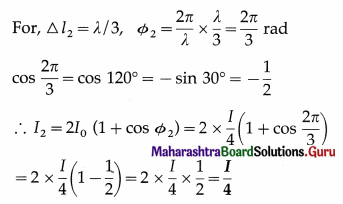
∴ A The intensity of light at a point where the path difference is λ/3 is λ/4.

Question 8.
The optical path difference between identical waves from two coherent sources and arriving at a point is 87λ. What can you say about the resultant intensity at the point? If the path difference is 49.19 μm, calculate the wavelength of light.
Solution :
Data : Path difference = 87λ = 49.19 /rm.
(i) Path difference = 87λ = nλ, where n = 87. As the path difference is an integral multiple of the wavelength λ, the point where the waves interfere is a bright point with maximum intensity.

(ii) 87 λ = 49.19 μn = 49.19 × 10^-6 m .
∴ λ = \(\frac{49.19 \times 10^{-6}}{87}\) = 5.654 × 10^-7 m = 5654 Å

Question 9.
The optical path difference between identical waves from two coherent sources and arriving at a point is 172. What can you say about the resultant intensity at the point? If the path difference is 9.18 μm, calculate the wavelength of light.
Solution :
Data : Path difference = 17λ = 9.18 μm
(i) Path difference = 17λ = nλ, where n = 17
As the path difference is an integral multiple of the wavelength λ, the point where the waves interfere is a bright point with maximum intensity.

(ii) 17λ = 9.18 μm = 9.18 × 10^-6 m

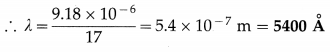
Question 10.
At a point on the two-slit interference pattern obtained using a source of green light of wavelength 5500 Å, the path difference is 4.125 pm. Is the point at the centre of a bright or dark fringe ? Hence, find the order of the fringe.
Solution :
Data : Path difference, ∆l = 4.125 × 10^-6 λ = 5500 Å = 5.5 × 10^-7 m

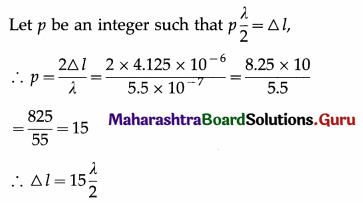
As the path difference is an odd integral multiple of \(\frac{\lambda}{2}\) the point is at the centre of a dark fringe.
∴ p = 2m – 1 (m = 1, 2, 3…)
∴ 2m – 1 = 15 ∴ m = 8
∴ The order of the fringe is 8 (i.e., the point lies at the centre of the 8th dark fringe.)

Question 11.
The two slits in an interference experiment are illuminated by light of wavelength 5600 A. Deter-mine the path difference and phase difference between the waves arriving at the centre of the eighth dark fringe on the screen.
Solution :
Data : λ = 5600 A = 5.6 × 10^-7 m
Order of the dark fringe is 8, ∴ m = 8
For the fringe to be dark, path difference
= (2m – 1)\(\frac{\lambda}{2}\)
∴ Path difference, ∆l = (2 × 8 – 1)\(\frac{\lambda}{2}\) = 7.5λ
= 7.5 × 5.6 × 10^-7 m
= 4.2 × 10^-6 m
Phase difference, φ = \(\frac{2 \pi}{\lambda}\) × ∆l
= \(\frac{2 \pi}{5.6 \times 10^{-7}}\) × 4.2 × 10^-6 = 15π

Question 12.
In Young’s double-slit experiment, interference fringes are observed on a screen 1 m away from the two slits which are 2 mm apart. A point P on the screen is 1.8 mm from the central bright fringe,
(i) Find the path difference at P.
(ii) If the wavelength of the light used in 4800 Å, what can you say about the illumination at P?
Solution :
Data : D = 1 m, d = 2 mm = 2 × 10^-3 m, y = 1.8 mm = 1.8 × 10^-3 m, λ = 4800 Å = 4.8 × 10^-7 m

∴ Path difference = 15\(\frac{\lambda}{2}\)
As the path difference is an odd integral multiple of \(\frac{\lambda}{2}\), point P is a dark point with minimum intensity.

Question 13.
Two slits 1.25 mm apart are illuminated by light of wavelength 4500 Å. The screen is 1 m away from the plane of the slits. Find the separation between the 2nd bright fringe on one side and the 2nd bright fringe on the other side of the central maximum.
Solution :
Data : D = 1 m, d = 1.25 mm = 1.25 × 10^-3 m,
λ = 4500 Å = 4500 × 10^-10 m = 4.5 × 10^-7 m
Since, it is a second bright fringe, n = 2. If s is the distance between the 2nd bright fringe on one side and the 2nd bright fringe on the other side of the central maximum, then
s = 2y = 2nλ\(\frac{D}{d}\)

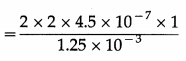
= 14.4 × 10^-4 m
W = 1.44 mm

Question 14.
A plane wavefront of light of wavelength 5000 Å is incident on two slits in a screen perpendicular to the direction of light rays. If the total separation of 10 bright fringes on a screen 2 m away is 4 mm, find the distance between the slits.
Solution:
Given : λ = 5000 Å = 5 × 10^-7 m,
D = 2 m and the total separation of 10 fringes = 4 mm = 4 × 10^-3 m

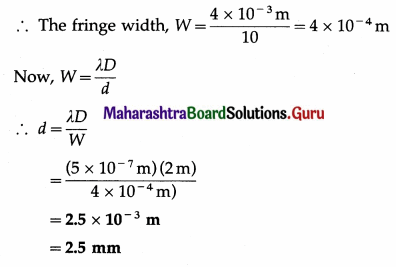
Question 15.
In Young’s double-slit experiment with slits of equal width, a point P on the screen is at a distance equal to one-fourth of the fringe width from the central maximum. If the intensity at the central maximum is I_c, find the intensity at P.
Solution :

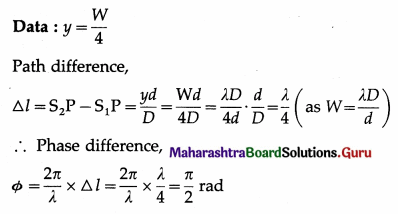
Since, the slits have equal width, the intensities of the two interfering waves are equal, say I₀. Then the intensity at a point on the screen is
I = 4I₀ cos² \(\frac{\phi}{2}\)
At the central maximum, φ = 0.

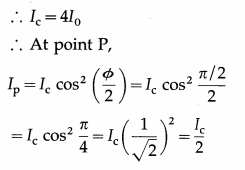
The intensity at P is half that at the central maximum.

Question 16.
In a double-slit experiment, the optical path difference between the waves coming from two coherent sources at a point P on one side of the central bright band is 7.5 × 10^-6 m and that at a point Q on the other side of the central bright band is 1.8 × 10^-6 m. How many bright and dark bands are observed between points P and Q if the wavelength of light used is 6 × 10^-7 m ?
Solution :
Data : ∆l₁ = 7.5 × 10^-6 m, ∆l₂ = 1.8 × 10^-6 m λ = 6 × 10^-7 m
For point P : Let p\(\frac{\lambda}{2}\) = ∆l₁

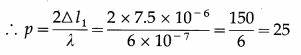
The path difference ∆l₁ is an odd integral multiple of λ/2 : ∆l₁ = (2m – 1)\(\frac{\lambda}{2}\), where m is an integer,
∴ 2m – 1 = 25 ∴ m = 13
∴ Point P is at the centre of the 13th dark band.
For point Q :
Let q\(\frac{\lambda}{2}\) = ∆l₂

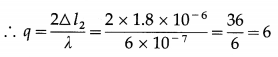
The path difference ∆l₂ is an even integral multiple of \(\frac{\lambda}{2}\) : ∆l₂ = (2n)\(\frac{\lambda}{2}\), where n is an integer
∴ 2n = 6 ∴ n = 3
∴ Point Q is at the centre of the 3rd bright band. Between points P and Q, excluding the respective bands at P and Q, the number of dark bands = 12 + 3 = 15 and the number of bright bands (including the central bright band) = 12 + 2 + 1 = 15

Question 17.
In Young’s double-slit experiment, light waves of wavelength 5.2 × 10^-7 m and 6.5 × 10^-7 m are used in turn keeping the same geometry. Compare the fringe widths in the two cases.
Solution :
Data : λ₁ = 5.2 × 10^-7 m, λ₂ = 6.5 × 10^-7 m
As, W = \(\frac{\lambda D}{d}\) and the geometry is the same, i.e., D and d remain the same,

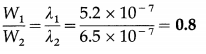
Question 18.
Two coherent sources are 1.8 mm apart and the fringes are observed on a screen 80 cm away from them. It is found that with a certain source of light, the fourth bright fringe is situated at a distance of 1.08 mm from the central fringe. Calculate the wavelength of light.
Solution :
Data : d = 1.8 mm = 1.8 × 10^-3 m
D = 80 cm = 0.8 m
For fourth bright fringe, n = 4

This is the wavelength of light.

Question 19.
Green light of wavelength 5100 Å from a narrow slit is incident on a double-slit. If the overall separation of 10 fringes on a screen 200 cm away from it is 2 cm, find the slit-separation.
Solution :
Data : λ = 5100 Å = 5.1 × 10^-7 m,
W = \(\frac{2}{10}\) cm = 2 × 10^-3 m,
D = 200 cm = 2 m
W = \(\frac{\lambda D}{d}\)
∴ d = \(\frac{\lambda D}{W}\) = \(\frac{5.1 \times 10^{-7} \times 2}{2 \times 10^{-3}}\)
= 5.1 × 10^-4 m
This is the slit-separation.

Question 20.
Sodium light of wavelength 5.896 × 10^-7 m is passed through two pinholes 0.5 mm apart, and an interference pattern is formed on a screen kept parallel to the plane of the pinholes and 1.2 m from them. Find the distance between
(i) the second and the fifth bright fringes
(ii) the third and the seventh dark fringes on the same side of the central bright point.
Solution :
Data : λ = 5.896 × 10^-7 m, d = 0.5 mm= 0.5 × 10^-3 m, D = 1.2 m
(i) The distance of the nth bright fringe from the central bright point is

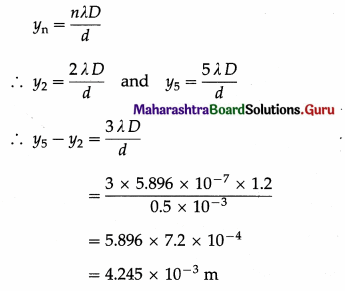
The distance between the second and the fifth bright fringes on the same side of the central bright point is 4.245 × 10^-3 m.

(ii) The distance of the mth dark fringe from the central bright point is

= 5.66 × 10^-3 m
The distance between the third and the seventh dark fringes on the same side of the central bright point is 5.66 × 10^-3 m.

Question 21.
In Young’s double-slit experiment, the two slits are 2 mm apart. The interference fringes for light of wavelength 6000Å are formed on a screen 80 cm away from them.
(i) How far is the second bright fringe from the central bright point?
(ii) How far is the second dark fringe from the central bright point?
Solution:
Data: D = 80 cm = 0.8 m,
d = 2 mm = 2 × 10^-3 m, λ = 6000Å = 6 × 10^-7 m
(i) For the second bright fringe from the central bright point, n = 2

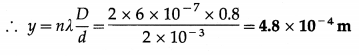
This is the required distance.

(ii) For the second dark fringe from the central bright point, m = 2

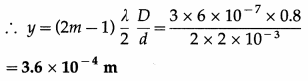
This is the required distance.

Question 21.
In Young’s double-slit experiment, the distance between two consecutive bright fringes on a screen placed at 1.5 m from the two slits is 0.6 mm. What would be the fringe width, if the screen is brought towards the slits by 50 cm, keeping rest of the setting the same?
Solution:
Let λ be the wavelengths of light used and d the distance between the two sources (i.e., slits), if D is the distance between the sources and the screen, the fringe width is
w = \(\frac{\lambda D}{d}\)
For the same λ and d, W ∝ D.
∴ \(\frac{W_{2}}{W_{1}}\) = \(\frac{D_{2}}{D_{1}}\)
Data:
W₁ = 0.6 mm = 6 × 10^-4 m,
D₁ = 1.5 m, D₂ = 1 m

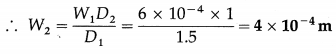
This is the required fringe width.

Question 22.
On passing light of wavelength 5000 Å through two pinholes 2 mm apart, an interference pattern is formed on a screen kept parallel to the plane of the pinholes and 100 cm from them. Find the distance between the fifth bright band on one side of the central bright band and the sixth dark band on the other side.
Solution :
Data : λ = 5000 Å = 5 × 10^-7 m, d = 2 mm = 2 × 10^-3 m, D = 100 cm = 1 m

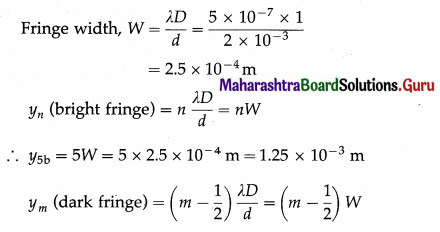
∴ y_6d = (6 – \(\frac{1}{2}\)) × 2.5 × 10^-4m = 1.375 × 10^-3 m
∴ y_5b + y_6d = 1.25 × 10^-3m + 1.375 × 10^-3m
= 2.625 × 10^-3 m = 2.625 mm
This is the required distance.

Question 23.
Monochromatic light from a narrow slit illuminates two narrow slits 3 mm apart, producing an interference pattern with bright fringes 0.15 mm apart on a screen 75 cm away from the slits. Find the wavelength of the light. How will the fringe width be altered if
(a) the distance of the screen from the slits is doubled
(b) the separation between the slits is doubled ?
Solution :
Data : d = 3 mm = 3 × 10^-3 m,
W = 0.15 mm = 1.5 × 10^-4 m, D = 75 cm = 0.75 m

Question 24.
In Young’s double-slit experiment the slits are 2 mm apart and interference is observed on a screen placed at a distance of 100 cm from the slits. It is found that the ninth bright fringe is at a distance of 2.208 mm from the second dark fringe from the centre of the fringe pattern. Find the wavelength of light used.
Solution :
Data : d = 2 mm = 2 × 10^-3 m,

Question 25.
In Young’s double-slit experiment, the two slits separated by 4 mm are illuminated by light of wavelength 6400 Å. Interference fringes are obtained on a screen placed at a distance of 60 cm from the slits. Find the change in the fringe width if the separation between the slits is
(i) increased by 1 mm
(ii) decreased by 1 mm.
Solution :
Data : d = 4 mm = 4 × 10^-3 m, λ = 6.4 × 10^-7m, D = 0.6 m, d’ = 5 mm = 5 × 10^-3 m, d” = 3 mm = 3 × 10^-3m
Fringe width, W = \(\frac{\lambda D}{d}\) ∴ W ∝ \(\frac{1}{d}\)
(i) Since d’ > d, W’ < W, i.e., the fringe width decreases.
Decrease in the fringe width = W – W

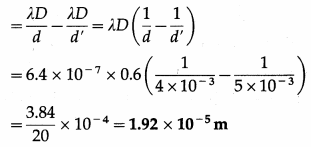
(ii) Since d” < d, W” > W, i.e., the fringe width increases.
Increase in the fringe width = W” – W

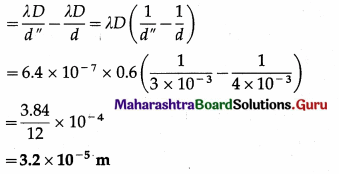
Question 26.
In Young’s double-slit experiment, the separation between the slits is 3 mm and the distance between the slits and the screen is 1 m. If the wavelength of light used is 6000 Å, calculate the fringe width. What will be the change in the fringe width if the entire apparatus is immersed in a liquid of refractive index \(\frac{4}{3}\)?
Solution :
Data : d = 3 × 10^-3 m, D = 1 m, λ = 6 × 10^-7 m, n = \(\frac{4}{3}\)

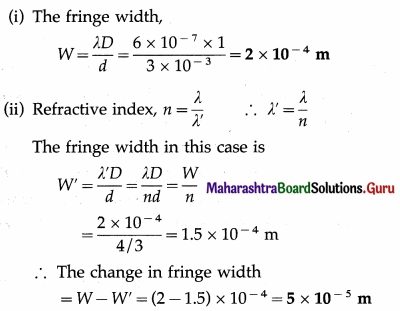
Question 27.
In Young’s double-slit experiment using monochromatic light, the fringe pattern shifts by certain distance on the screen when a mica sheet of refractive index 1.6 and thickness 1.964 microns is introduced in the path of one of the interfering waves. The mica sheet is then removed and the slits-to-screen distance is doubled. It is found that the distance between successive maxima now is the same as the observed fringe shift with the mica sheet. Calculate the wavelength of the monochromatic light used.
Solution :
Data : n_m = 1.6, b = 1.964 microns
= 1.964 × 10^-6 m,
D₂ = 2D₁, W₂ = y₀
The fringe shift with the mica sheet,
y₀ = \(\frac{D_{1}}{d}\)(n_m – 1)b
Subsequent to the removal of the mica sheet and doubling the slits-to-screen distance, the new fringe width is,

Question 28.
What must be the thickness of a thin film which, when kept near one of the slits shifts the central fringe by 5 mm for incident light of wavelength 5890 Å in Young’s double-slit interference experiment ? The refractive index of the material of the film is 1.1 and the distance between the slits is 0.5 mm.
Solution :
Data : λ = 5890 Å, nm = 1.1, the shift of the central bright fringe = 5 mm

Let t be the thickness of the film and P the point on the screen where the central fringe has shifted. Suppose the film is kept in front of slit S1. Due to the film, the optical path travelled by the light passing through it increases by (1.1 – 1)f = 0.1t. Thus, the optical paths between the two beams passing through the two slits are not equal at the midpoint of the screen but are equal at P, 5 mm away from the centre. At this point the distance travelled by light from the other slit S₂ to the screen is larger than that travelled by light from S₁ by 0.1t.

The difference in distances, S₂P – S₁P = yλ/d, where y is the distance along the screen = 5 mm = 5 × 10^-3m and d = 0.5 mm = 5 × 10^-4 m.

This has to be equal to the difference in optical paths introduced by the film.
Thus, 0.1t = 5 × 10^-3 × 5890 × 10^-10/5 × 10^-4.
∴ t = 5890 × 10^-8m = 5.89 × 10^-5 m = 0.0589 mm

Question 29.
In a biprism experiment, the eyepiece is placed at a distance of 1.2 metres from the source. The distance between the virtual sources was found to be 7.5 × 10^-4 m. Find the wavelength of light if the eyepiece is to be moved transversely through a distance of 1.888 cm for 20 fringes.
Solution :
Data : D = 1.2 m, d = 7.5 × 10^-4 m,
20 W = 1.888 cm = 1.888 × 10^-2 m

Question 30.
A biprism is placed 5 cm from the slit illuminated by sodium light of wavelength 5890 Å. The width of the fringes obtained on a screen 75 cm from the biprism is 9.424 × 10^-2 cm. What is the distance between the two coherent sources?
Solution :
Data : D = 5 cm + 75 cm = 80 cm = 0.8 m,
λ = 5890 Å = 5.890 × 10^-7 m,
W = 9.424 × 10^-2 cm = 9.424 × 10^-4 m
Fringe width, W = \(\frac{\lambda D}{d}\)
∴ The distance between the two coherent sources,

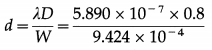
= 5 × 10^-4 m = 0.5 mm

Question 31.
In a biprism experiment, the distance of the 20th bright band from the centre of the interference pattern is 8 mm. Calculate the distance of the 30th bright band from the centre.
Solution :
Data : y₂₀ = 8 mm (bright band)
The distance of the nth bright band from the centre of the interference pattern,

The distance of the 30th bright band from the centre of the interference pattern is 12 mm.

Question 32.
In a biprism experiment, a source of light having wavelength 6500 Å is replaced by a source of light having wavelength 5500 Å. Calculate the change in the fringe width, if the screen is at a distance of 1 m from the sources which are 1 mm apart.
Solution :

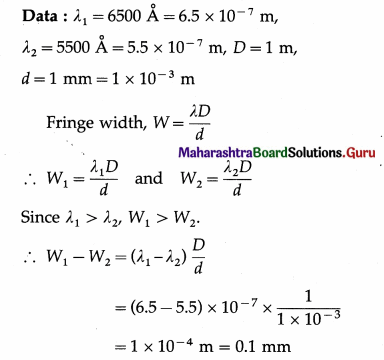
The fringe width decreases by 1 × 10^-4 m = 0.1 mm.

Question 33.
In a biprism experiment, light of wavelength 5200 Å is used to get an interference pattern on the screen. The fringe width changes by 1.3 mm when the screen is moved towards the biprism by 50 cm. Find the distance between the two virtual images of the slit.
Solution :
Data : λ = 5200 Å = 5.2 × 10^-7 m,
W₁ – W₂ = 1.3 mm = 1.3 × 10^-3 m,
D₁ – D₂ = 50 cm = 0.5 m

This is the distance between the two virtual sources.

Question 34.
In a biprism experiment, the 10th dark band is observed at 2.09 mm from the central bright point on the screen with red light of wavelength 6400 Å. By how much will the fringe width change if blue light of wavelength 4800 A is used with the same setting?
Solution :

Question 35.
In a biprism experiment, the slit is illuminated by red light of wavelength 6400 Å, and the cross wire of the eyepiece is adjusted at the centre of the 3rd bright band. On using blue light, it is found that the 4th bright band is on the cross wire. Find the wavelength of blue light.
Solution :
Data : λ_r = 6400 Å, y₃ (red, bright)

This is the wavelength of blue light.

Question 36.
In a biprism experiment, the wavelength of red light used is 6000 Å and the nth bright band is obtained at a point P on the screen. Keeping the same setting, the source is replaced by a source of green light of wavelength 5000 Å and the (n + 1)th bright band of green light coincides with point P. Find n.
Solution :

Question 37.
In a biprism experiment, the slit is illuminated by light of wavelength 4800 Å. The distance between the slit and the biprism is 15 cm and that between the biprism and the eyepiece is 85 cm. If the distance between the virtual sources is 3 mm, determine the distance between the 4th bright band on one side and the 4th dark band on the other side of the central band.
Solution :
Data : λ = 4800 Å = 4.8 × 10^-7 m,
d = 3 mm = 3 × 10^-3 m,
D = distance between the slit and the biprism + distance between the biprism and the eyepiece = 15 + 85 = 100 cm = 1 m The distance of the nth bright band from the central band is

This is the required distance.

Question 38.
An isosceles prism of refracting angle 179° and refractive index 1.6 is used as a biprism by keeping it 10 cm away from a slit, the edge of the biprism being parallel to the slit. The slit is illuminated by a light of wavelength 600 nm and the screen is 90 cm away from the biprism. Calculate the location of the centre of the 10th dark band from the centre of the interference pattern and the path difference at this location.
Solution :

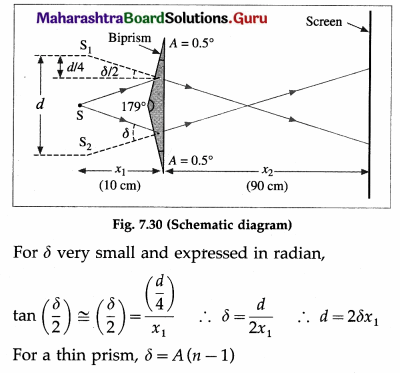
Question 39.
In a biprism experiment, the distance between the second and tenth dark bands on the same side of the central bright band is 0.12 cm, that between the slit and the biprism is 20 cm and that between the biprism and the eyepiece is 80 cm. If the slit images given by the lens in the two positions are 4.5 mm and 2 mm apart, find the wavelength of light used.
Solution :
The distance between the second and tenth dark bands on the same side of the central band is equal to 8 times the fringe width (W).
∴ 8 W = 0.12 cm (by the data)
∴ W = \(\frac{0.12}{8}\) cm = 0.015 cm = 0.015 × 10^-2 m
The distance (D) between the slit and the eyepiece is equal to the sum of the distance between the slit and the biprism and the distance between the biprism and the eyepiece.
∴ D = 20 + 80 = 100 cm = 1 m (by the data)
Also, d₁ = 4.5 mm and d₂ = 2 mm
∴ The distance (d) between the virtual images of the slit is
d = \(\sqrt{d_{1} d_{2}}\) = \(\) mm = 3 mm
= 3 × 10^-3 m
∴ The wavelength of light,

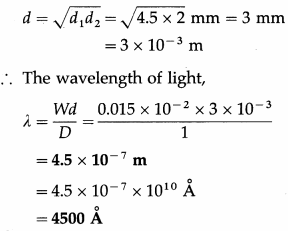
Question 40.
In a biprism experiment, the slit and the eyepiece. are 10 cm and 80 cm away from the biprism. When a convex lens was interposed at 30 cm from the slit, the separation of the two magnified images of the slit was found to be 4.5 mm. If the wavelength of the source is 4500 Å, calculate the fringe width.
Solution:
Data : d₁ = 4.5 mm = 4.5 × 10^-3 m,
λ = 4500 Å = 4.5 × 10^-7 m,
distance between the slit and the eyepiece (D) = distance between the slit and the biprism + distance between the biprism and the eyepiece = 10 cm + 80 cm = 90 cm = 0.9 m, u₁ = 30 cm = 0.3 m v₁ = D – u₁ = 0.9m – 0.3m = 0.6 m
Linear magnification of a lens,

Question 65.
Describe with a neat labelled ray diagram the Fraunhofer diffraction pattern due to a single slit. Obtain the expressions for the positions of the intensity minima and maxima. Also obtain the expression for the width of the central maximum.
Answer:
When a parallel beam of monochromatic light of wavelength λ illuminates a single slit of finite width a, we observe on a screen some distance from the slit, a broad pattern of alternate dark and bright fringes. The pattern consists of a central bright fringe, with successive dark and bright fringes of diminishing intensity on both sides. This is called ‘ the diffraction pattern of a single slit.

Consider a single slit illuminated with a parallel beam of monochromatic light perpendicular to the plane of the slit. The diffraction pattern is obtained on a screen at a distance D (» a) from the slit and at the focal plane of the convex lens.

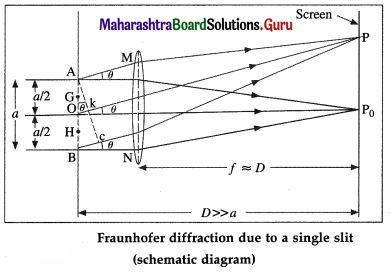
We can imagine the single slit as being made up of a large number of Huygens’ sources evenly distributed over the width of the slit. Then the maxima and minima of the pattern arise from the interference of the various Huygens’ wavelets.
Now, imagine the single slit as made up of two adjacent slits, each of width a/2. Since, the incident plane wavefronts are parallel to the plane of the slit, all the Huygens sources at the slit will be in phase. They will therefore also in phase at the point P₀ on the screen, where P₀ is equidistant from all the Huygens sources. At P₀, then, we get the central maximum.

For the first minimum of intensity on the screen, the path difference between the waves from the Huygens sources A and O (or O and B) is λ/2, which is the condition for destructive interference. Suppose, the nodal line OP for the first minimum subtends an angle θ at the slit; θ is very small. With P as the centre and PA as radius, strike an arc intersecting PB at C. Since, D » a, the arc AC can be considered a straight line at right angles to PB. Then, ∆ ABC is a right-angled triangle similar to A OP₀P.
This means that, ∠BAC = θ
∴ BC = a sin θ
∴ Difference in path length,
BC = PB – PA = (PB – PO) + (PO – PA)

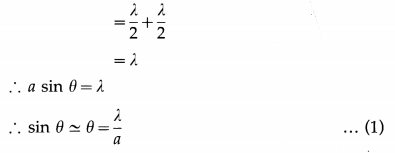
(∵ θ is very small and in radian)
The other nodal lines of intensity minima can be understood in a similar way. In general, then, for the with minimum (wi = +1, ±2, ±3, …).
θ_m = \(\frac{m \lambda}{a}\) (with minimum) … (2)
as θ_m is very small and in radian.
Between the successive minima, the intensity rises to secondary maxima when the path difference is an odd-integral multiple of \(\frac{\lambda}{2}\) :

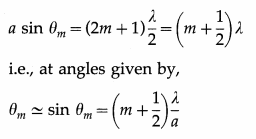
(mth secondary maximum) … (3)
Width of the central maximum :
Equation (1) gives the angular half width of the central maximum. Therefore, the angular width of the central maximum is,
2θ = \(\frac{2 \lambda}{a}\) … (4)
From ∆OP₀P, P₀P = D tan θ \(\simeq\) D sin θ
(∵ θ is very small and in radian)
∴ y₁ = P₀P = \(\frac{D \lambda}{a}\) [from Eq. (1)] … (5)
This is the distance of the first minimum from the centre of the central maximum.
∴ Width of the central bright fringe :
W_c = 2y_1d = 2W = 2\(\left(\frac{\lambda D}{a}\right)\) …(6)

The central bright fringe is spread between the first dark fringes on either side. Thus, the width of the central bright fringe is the distance between the centres of the first dark fringe on either side.

If the lens is very close to the slit, D is very nearly equal to f, where f is the focal length of the lens. Then W_c = 2\(\left(\frac{\lambda D}{a}\right)\) = 2\(\left(\frac{\lambda f}{a}\right)\) … (7)

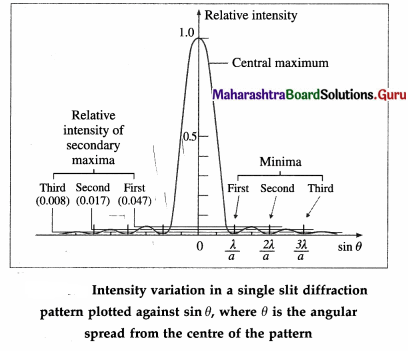
Question 66.
Represent graphically intensity distribution in
(a) Young’s double-slit interference
(b) single- slit diffraction and
(c) double-slit diffraction
Answer:

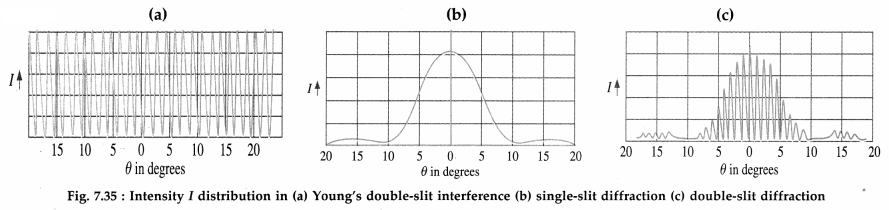
Question 67.
State the characteristics of a single-slit diffraction pattern.
Answer:
Characteristics of a single-slit diffraction pattern :

1. The image cast by a single-slit is not the expected purely geometrical image.
2. For a given wavelength, the width of the diffraction pattern is inversely proportional to the slit width.
3. For a given slit width a, the width of the diffraction pattern is proportional to the wavelength.
4. The intensities of the non-central, i.e., secondary, maxima are much less than the intensity of the central maximum.
5. The minima and the non-central maxima are of the same width, Dλ/a.
6. The width of the central maximum is 2Dλ/a. It is twice the width of the non-central maxima or minima.

Question 68.
Explain briefly the double-slit diffraction pattern.
Answer:
The double-slit diffraction pattern is determined by the diffraction patterns due to the individual slits, and by the interference between them.

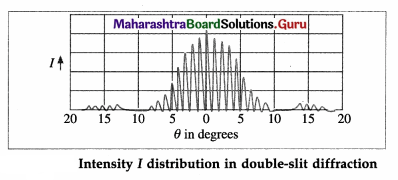
We can see narrow interference fringes similar to those obtained in Young’s double-slit experiment. These fringes vary in brightness and the shape of their envelope as that of the single-slit diffraction pattern.

Question 69.
What should be the order of the size of an obstacle or aperture to produce diffraction of light?
Answer:
For pronounced diffraction, the size of an obstacle or aperture should be of the order of the wavelength of light or greater.
[Note : For diffraction from a single slit of width a with monochromatic light of wavelength λ, the condition for first minimum (dark fringe) is
sin θ₁ = \(\frac{\lambda}{a}\)
When a = λ, θ₁ = 90° and the central maximum spreads over 180°; then, while the diffraction is maximum, no fringe pattern is seen at all.

When a » X (say, a is of the order of a centimetre or more), θ₁ is so small that there is practically no diffraction and the illuminated region on the screen is almost as given by geometrical optics. However, diffraction pattern due to a straight-edge will always be seen at the edge of the illuminated region. Hence, for an observable fringe pattern due to a single slit, a should be of the order of X with a > λ..]

Question 70.
Solve the following.

Question 1.
Plane waves of light from a sodium lamp are incident on a slit of width 2 μm. A screen is located 2 m from the slit. Find the spacing between the first secondary maxima of two sodium lines as measured on the screen.
(Given : λ₁ = 5890 Å and ₂ = 5896 Å)
Solution:


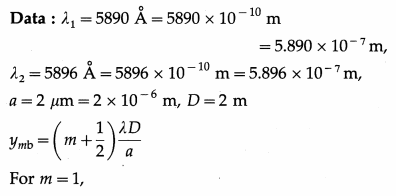
This is the required spacing.

Question 2.
The diffraction pattern of a single slit of width 0. 5 cm is formed by a lens of focal length 40 cm. Calculate the distance between the first dark and the next bright fringe from the axis. The wavelength of light used is 4890 Å.
Solution :
Data : a = 0.5 cm = 0.5 × 10^-2 m,
D \(\simeq\) f = 40 cm = 0.4 m, λ = 4890 Å = 4.890 × 10^-7 m
The distance between the first dark fringe and the next bright fringe = \(\frac{\lambda D}{2 a}\)

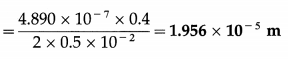
Question 3.
Light of wavelength 6000 Å is incident on a slit of width 0.3 mm. A screen is placed parallel to the slit 2 m away from the slit. Find the position of the first dark fringe from the centre of the central maximum. Also, find the width of the central maximum.
Solution :
Data : λ = 6 × 10^-7 m, a = 0.3 mm = 3 × 10^-4 m,
D = 2 m
The distance y_m of the m th minimum from the centre of the central maximum is

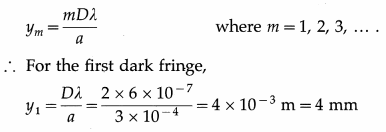
The first dark fringe is 4 mm from the centre of the central fringe.
∴ Half-width of the central maximum = 4 mm
∴ The width of the central maximum = 2 × 4 mm = 8 mm

Question 4.
In a single-slit diffraction pattern, the distance between the first minimum on the right and the first minimum on the left is 5.2 mm. The screen on which the pattern is displayed is 80 cm from the slit and the wavelength of light is 5460 Å. Calculate the slit width.
Solution :
Data : y₁ (minimum, right) + y₁ (minimum, left)

Question 5.
In a single-slit diffraction pattern, the distance between the first minimum on the right and the first minimum on the left of the central maximum is 4 mm. The screen is 2 m from the slit and the wavelength of light used is 6000 Å. Calculate the width of the slit and the width of the central maximum.
Solution :
Data : y₁ (minimum, right) + y₁ (minimum, left)
= 4 mm = 4 × 10^-3 m, D = 2 m, λ = 6 × 10^-7 m

Question 6.
Determine the angular spread between the central maximum and first order maximum of the diffraction pattern due to a single slit of width 0.25 mm, when light of 6650 Å is incident on it normally.
Solution:
Data : λ = 6650 Å = 6650 × 10^-10m, a = 0.25 mm

This is the required angular spread.

Question 71.
Explain and define the resolving power of an optical instrument.
Answer:
Resolving power of an optical instrument:
The primary aim of using an optical instrument is to see fine details, whether observing a star system through a telescope or a living cell through a microscope. After passing through an optical system, light from two adjacent parts of the object should produce sharp, distinct (separate) images of those parts. The objective lens or mirror of a telescope or microscope acts like a circular aperture. The diffraction pattern of a circular aperture consists of a central bright spot (called the Airy disc and corresponds to the central maximum) and concentric dark and bright rings.

Light from two close objects or parts of an object after passing through the aperture of an optical system produces overlapping diffraction patterns that tend to obscure the image. If these diffraction patterns are so broad that their central maxima overlap substantially, it is difficult to decide if the intensity distribution is produced by two separate objects or by one.

The resolving power of an optical instrument, e.g., a telescope or microscope, is a measure of its ability to produce detectably separate images of objects that are close together.

Definition : The smallest linear or angular separation between two point objects which appear just resolved when viewed through an optical instrument is called the limit of resolution of the instrument and its reciprocal is called the resolving power of the instrument.

Question 72.
State and explain Rayleigh’s criterion for minimum resolution.
Answer:
Rayleigh’s criterion for minimum resolution : Two overlapping diffraction patterns due to two point sources are acceptably or just resolved if the centre of the central peak of one diffraction pattern is as far as the first minimum of the other pattern.

The ‘sharpness’ of the central maximum of a diffraction pattern is measured by the angular separation between the centre of the peak and the first minimum. It gives the limit of resolution.

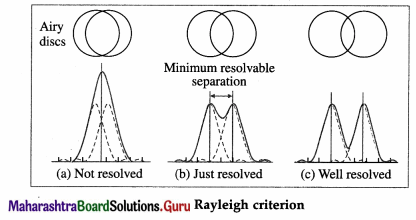
Two overlapping diffraction patterns due to two point sources are not resolved if the angular separation between the central peaks is less than the limit of resolution. They are said to be just separate, or resolved, if the angular separation between the central peaks is equal to the limit of resolution. They are said to be well resolved if the angular separation between the central peaks is more than the limit of resolution.

Question 73.
Explain the Rayleigh criterion for the limit of resolution for
(i) two linear objects
(ii) a pair of point objects.
Answer:
(i) The Rayleigh criterion for the limit of resolution for two linear objects : Consider, two self luminous objects or slits separated by some distance. Let λ be the wavelength of the light and a the width of the slits. As per the Rayleigh criterion, the first minimum of the diffraction pattern of one of the sources should coincide with the central maximum of the other. Thus, it is at the just resolved condition.
The angular separation dθ (position) of the first principal minimum is,
dθ = \(\frac{\lambda}{a}\) …(1)
This angular separation between the two objects must be minimum as this minimum coincides with the central maximum of the other. This is called the limit of resolution of that instrument. It is written as,
limit of resolution, dθ = \(\frac{\lambda}{a}\)
Minimum separation between the two linear objects that are just resolved, at distance D from the instrument is, ni
y = D(dθ) = \(\frac{D \lambda}{a}\) …(2)
It is the distance of the first minimum from the centre.

(ii) The Rayleigh criterion for the limit of resolution for a pair of point objects : The objects to be viewed through a microscope are often of the point-size. The diffraction pattern of such objects consists of a central bright spot called the Airy disc and corresponds to the central maximum surrounded by concentric dark and bright rings called Airy rings.

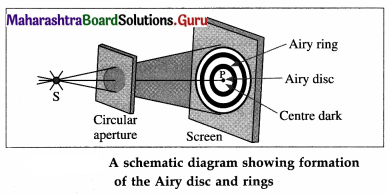
If a red laser beam passes through a 90 µm pinhole aperture, the Airy disc and several orders (rings) of diffraction are as shown.

According to Lord Rayleigh, for such objects to be just resolved, the first dark ring of the diffraction pattern of the first object should be formed at the centre of the diffraction pattern of the second object and vice versa. Thus, the minimum separation between the images on the screen should be equal to the radius of the first dark ring.
This is applicable to the eye, microscope, telescope, etc.

Question 74.
Define and explain the resolving power of a microscope. State the expressions for the resolving power of
(i) a microscope with a pair of non-luminous objects
(ii) a microscope with self luminous point objects.
OR
What is meant by the limit of resolution and the resolving power of a microscope?
Answer:
Definition : The limit of resolution of a microscope is the least separation between two-closely spaced points on an object which are just resolved when viewed through the microscope.

Definition : The resolving power of a microscope is defined to be the reciprocal of its limit of resolution.

In a compound microscope, the objective lens forms a real, magnified image of an object placed just beyond the focal length of the lens. The objective has a short focal length (for greater magnification) and is held close to the object so that it gathers as much of the light scattered by the object as possible.

Let a be the least separation between two point objects O and O’ viewed through an objective AB of a compound microscope. The medium between the object and the objective has a refractive index n. The images of the objects O and O’ are I and I’ respectively. In this case, the angular separation between the objects, at the objective is 2α. D is the diameter of the objective AB.

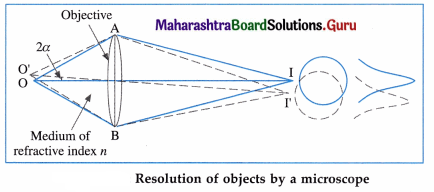
According to the Rayleigh criterion, the first dark ring due to O’ should coincide with I and that of O should coincide with I’. The nature of illumination at a point on the screen is determined by the effective path difference at that point. Let us consider point I to be symmetric with respect to O. Paths of the extreme rays reaching I from O’ are O’AI and O’BI. The paths AI and BI are equal. Thus, the actual path difference is O’B – O’A.

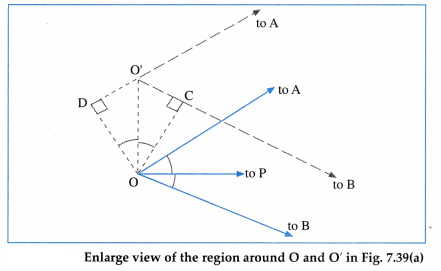
The enlarged view of the region around O and O’ is as shown.
From this,
path difference = DO’ + O’C
= 2a sin α

(i) Microscope with a pair of non-luminous objects (dark objects):
In actual practice, the objects O and O’ viewed through a microscope are illuminated by the same source. Often the eyepiece of the microscope is filled with some transparent material of refractive index n. Then the wavelength of light in this material is
λ_n = \(\frac{\lambda}{n}\) where λ is the wavelength of light in air.

In such a set up the path difference at the first dark ring in λ_n. Thus, from eq (1),

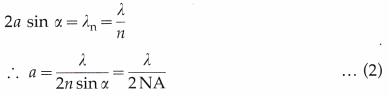
The factor n sin a is called numerical aperture (NA). The resolving power of the microscope is
R = \(\frac{1}{a}\) = \(\frac{2 \mathrm{NA}}{\lambda}\) …. (3)

(ii) Microscope with self luminous point objects : Applying Abbe’s theory of Airy discs and rings to Fraunhofer diffraction due to a pair of self luminous point objects, the path difference between the extreme rays, at the first dark ring is 1.22 λ, thus, for the requirement of just resolution,

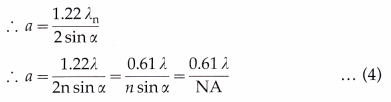
The resolving power of the microscope is,
R = \(\frac{1}{a}\) = \(\frac{\mathrm{NA}}{0.61 \lambda}\) …. (5)
When the value of a is minimum, the quality of resolution is high.
Notes:

1. If f and D are the focal length and the diameter of the microscope objective.
   sin i_max \(\simeq \frac{D / 2}{f}\) so that Eq. (3) can be written as resolving power = \(\frac{n D}{f \lambda}\)
2. Ernst Abbe(1840 -1905), German physicist and developer of optical instruments.

Question 75.
Explain why microscopes of high magnifying power have oil filled (oil-immersion) objectives.
Answer:
Higher angular magnification of a high magnifying power microscope is of little use if the finer details in a tiny object are obscured by diffraction effects. Hence, a microscope of high magnifying power must also have a high resolving power.
Resolving power ot a microscope = \(\frac{2 n \sin \alpha}{\lambda}\)
Where α ≡ the half angle of the angular separation between the objects, at the objective lens. n ≡ the refractive index of the medium between the object and the objective, λ ≡ the wavelength of the light used to illuminate the object.

The factor n sin α is called the numerical aperture of the objective and the resolving power increases with increase in the numerical aperture. To increase α the diameter of the objective would have to be increased. But this increase in aperture would degrade the image by decreasing the resolving power. Hence, in microscopes of high magnifying power, the object is immersed in oil that is in contact with the objective. Usually cedarwood oil having a refractive index 1.5 (close to that of the objective glass) is used. Closeness of the refractive indices also reduces loss of light by reflection at the objective lens.

Question 76.
On what factors does the resolving power of a microscope depend? How can it be increased?
Answer:
Resolving power of a microscope
= \(\frac{2 n \sin \alpha}{\lambda}\) = \(\frac{2 \mathrm{NA}}{\lambda}\)

where, α ≡ the half angle of the angular separation between the objects at the objective lens. n ≡ the refractive index of the medium between the object and the objective, λ ≡ the wavelength of the light used to illuminate the object, NA = n sin α = the numerical aperture of the objective.

Thus, the resolving power of a microscope depends directly on the NA and inversely on λ.
The resolving power is increased by,

1. increasing the numerical aperture using oil-immersion objective.
2. illuminating the object with smaller wavelength radiation. But our eyes are not very sensitive to the shorter wavelength blue end of the visible spectrum. Hence, ultraviolet radiation is used for illumination with quartz lenses, but then photographs must be taken to examine the image.

Question 77.
With a neat ray diagram, explain the resolving power of a telescope. On what factors does it depend ?
OR
What is meant by the angular limit of resolution and resolving power of a telescope?
Answer:
The resolving power of a telescope is defined as the reciprocal of the angular limit of resolution between two closely-spaced distant objects so that they are just resolved when seen through the telescope.

Consider two stars seen through a telescope. The diameter (D) of the objective lens or mirror corresponds to the diffracting aperture. For a distant point source, the first diffraction minimum is at an angle θ away from the centre such that

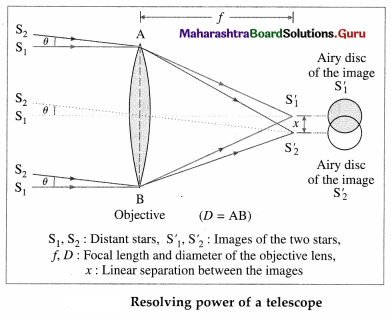
Dsin θ = 1.22 λ
where λ is the wavelength of light. The angle 9 is usually so small that we can substitute sin θ \(\approx\) θ (θ in radian). Thus, the Airy disc for each star will be spread out over an angular half-width θ = 1.22 λ/D about its geometrical image point. The radius of the Airy disc at the focal plane of the objective lens is r = fθ = 1.22fλ/D, where f is the focal length of the objective.

When observing two closely-spaced stars, the Rayleigh criterion for just resolving the images as that of two point sources (instead of one) is met when the centre of one Airy disc falls on the first minimum of the other pattern. Thus, the angular limit (or angular separation) of resolution is
θ = \(\frac{1.22 \lambda}{D}\) … (1)

and the linear separation between the images at the focal plane of the objective lens is
y = fθ … (2)
∴ Resolving power of a telescope.
R = \(\frac{1}{\theta}\) = \(\frac{D}{1.22 \lambda}\) … (3)

It depends

1. directly on the diameter of the objective lens or mirror,
2. inversely on the wavelength of the radiation.

Question 78.
How can the resolving power of a telescope be increased?
Answer:
The resolving power of an astronomical telescope depends directly on the diameter of the objective lens or mirror, and inversely on the wavelength of radiation. Hence, the resolving power can be increased by

1. using an objective lens/mirror of larger diameter
2. observing a celestial object at smaller wavelengths.

Question 79.
Define the resolving power of a telescope and state its formula. What are the advantages of using a large objective lens in an astronomical telescope:
Answer:
Definition: The resolving power of a telescope is defined as the reciprocal of the angular limit of resolution between two closely-spaced distant objects so that they are just resolved when seen through the telescope.
Formula : Resolving power of a telescope
R = \(\frac{1}{\theta}\) = \(\frac{D}{1.22 \lambda}\)
where θ ≡ the minimum angular separation of two closely-spaced celestial objects or the angular limit of resolution, D ≡ the diameter of the objective lens of the telescope, λ ≡ the wavelengh of light.

Advantages of a large objective lens in an astronomical telescope :

1. The resolving power is directly proportional to the diameter of the objective lens. Hence, a large objective lens results in a smaller Airy disc and a sharper image.
2. It collects more of the incident radiation from a distant object which results in a brighter image.

Question 80.
What is the resolving power of a telescope if the diameter of the objective of the telescope is 1.22 m and the wavelength of light is 5000 Å ?
Answer:
Resolving power of the telescope = \(\frac{D}{1.22 \lambda}\)
= \(\frac{1.22}{1.22 \times 5 \times 10^{-7}}\)
= \(\frac{10 \times 10^{6}}{5}\) = 2 × 10⁶ rad^-1

Question 81.
Briefly explain about radio telescope.
Answer:
A radio telescope is an astronomical instrument consisting of a radio receiver and an antenna system used to detect radio-frequency radiation emitted by extraterrestrial sources. The wavelength of radio-frequency radiation is very long. Hence, it is expressed in metre. In order to attain the resolution of an optical telescope, the radio telescope should be very large. A single disc of such large diameters is impracticable. In such cases arrays of antennae spread over several kilometres are used. Giant Metrewave Radio Telescope (GMRT) located at Narayangaon, Pune, Maharashtra uses such an array consisting of 30 dishes of diameter 45 m each. It spreads over 25 km. It is the largest distance between two of its antennae. The highest angular resolution achievable ranges from about 60 arcsec at the lowest frequency of 50 MHz to about 2 arcsec at 1.4 GHz.

Question 82.
Solve the following :

Question 1.
Light of wavelength 650 nm falls on the objective of a microscope having total angle of angular w separation as 60°. Calculate the resolving power of the microscope. [Refractive index of air = 1]
Solution :
Data : λ = 650 nm = 6.5 × 10^-7m, n = 1,
2α = 60°
∴ α = 30°
Resolving power of the microscope = \(\frac{2 n \sin \alpha}{\lambda}\)
= \(\frac{2 \times 1 \times \sin 30^{\circ}}{6.5 \times 10^{-7}}\) = \(\frac{10}{6.5}\) × 10⁶

Question 2.
The semi vertical angle of the cone of the rays incident on the objective of a microscope is 20°. If the wavelength of incident light is 6600 Å, calculate the smallest distance between two points which can be just resolved.
Solution :
Data : α = 20°, λ = 6600 Å = 6.6 × 10^-7 m, n = 1 (air) resolution between two closely-spaced distant objects so that they are just resolved when seen through the telescope.
Formula : Resolving power of a telescope
R = \(\frac{1}{\theta}\) = \(\frac{D}{1.22 \lambda}\)
where θ ≡ the minimum angular separation of two closely-spaced celestial objects or the angular limit of resolution, D ≡ the diameter of the objective lens of the telescope, λ ≡ the wavelengh of light.

Advantages of a large objective lens in an astronomical telescope :

1. The resolving power is directly proportional to the diameter of the objective lens. Hence, a large objective lens results in a smaller Airy disc and a sharper image.
2. It collects more of the incident radiation from a distant object which results in a brighter image.

Question 83.
What is the resolving power of a telescope if the diameter of the objective of the telescope is 1.22 m and the wavelength of light is 5000 Å ?.
Answer:
Resolving power of the telescope = \(\frac{D}{1.22 \lambda}\)

Question 84.
Briefly explain about radio telescope.
Answer:
A radio telescope is an astronomical instrument consisting of a radio receiver and an antenna system used to detect radio-frequency radiation emitted by extraterrestrial sources. The wavelength of radio-frequency radiation is very long. Hence, it is expressed in metre. In order to attain the resolution of an optical telescope, the radio telescope should be very large. A single disc of such large diameters is impracticable. In such cases arrays of antennae spread over several kilometres are used. Giant Metrewave Radio Telescope (GMRT) located at Narayangaon, Pune, Maharashtra uses such an array consisting of 30 dishes of diameter 45 m each. It spreads over 25 km. It is the largest distance between two of its antennae. The highest angular resolution achievable ranges from about 60 arcsec at the lowest frequency of 50 MHz to about 2 arcsec at 1.4 GHz.

Question 85.
Solve the following :

Question 1.
Light of wavelength 650 nm falls on the objective of a microscope having total angle of angular separation as 60°. Calculate the resolving power of the microscope. [Refractive index of air = 1]
Solution :
Data : λ = 650 nm = 6.5 × 10^-7m, n = 1, 2α = 60°
∴ α = 30°
Resolving power of the microscope = \(\frac{2 n \sin \alpha}{\lambda}\)

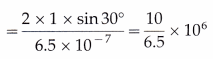
= 1.538 × 10⁶ m^-1

Question 2.
The semi vertical angle of the cone of the rays incident on the objective of a microscope is 20°. If the wavelength of incident light is 6600 Å, calculate the smallest distance between two points which can be just resolved.
Solution :
Data : α = 20°, λ = 6600 Å = 6.6 × 10^-7 m, n = 1 (air)
The numerical aperture, NA = n sin α
= 1 × sin 20° = 0.3420
The limit of resolution for an illuminated object,

Question 3.
What is the minimum distance between two objects which can be resolved by a microscope having the visual angle of 30° when light of wavelength 600 nm is used ?
Solution :

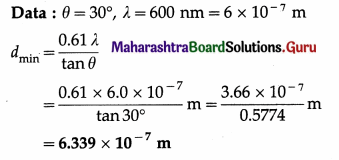
Question 4.
The two headlights of an approaching automobile are 1.22 m apart. At what maximum distance will eye resolve them? Assume a pupil diameter of 5.0 mm and λ = 5500 Å. Assume also that this distance is determined only by the diffraction effect at the circular aperture.
Solution:
Data : y = 1.22 m, diameter D = 5 × 10^-3 m,

This is the required distance.

Question 5.
What is the minimum angular separation between two stars if a telescope is used to observe them with an objective of aperture 20 cm? The wavelength of light is 5900 Å.
Solution :
Data : D = 20 cm = 0.2 m,
λ = 5900 Å = 5.9 × 10^-7 m

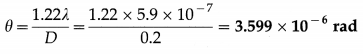
This is the required angular separation.

Question 6.
The diameter of the objective of a telescope is 10 cm. Find the resolving power of the telescope is 10 cm. Find the resolving power of the telescope if the wavelength of light is 5000 Å.
Solution :
Data : D = 10 cm = 0.1 m, λ = 5000 Å = 5 × 10^-7 m
The resolving power of the telescope D 0.1

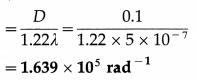
Question 7.
A telescope has an objective of diameter 2.44 m. What is its angular resolution when it observes at 5500 A?
Solution :
Data : λ = 5500A = 5.5 × 10^-7 m,
D = 2.44 m
Angular resolution. ∆θ = 1.22λ/D, D being the diameter of the aperture.
∴ ∆θ = 1.22 × 5.5 × \(\frac{10^{-7}}{2.44}\)= 2.75 × 10^-7 rad
= 0.0567 arcsec

Question 8.
The minimum angular separation between two stars is 4 × 10^-6 rad when a telescope is used to observe them with an objective of aperture 16 cm. Find the wavelength of the light.
Solution :
Data : θ = 4 × 10^-6 rad, D = 16 cm = 0.16 m
θ = \(\frac{1.22 \lambda}{D}\)
∴ The wavelength of the light used,

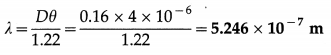
Question 9.
Estimate the smallest angular separation of two stars which can be just resolved by the telescope having objective of diameter 25 cm. The mean wavelength of light is 555 nm.
Solution :
Data : λ = 555 nm 555 × 10^-9 m
D = 25 cm = 25 × 10^-2 m

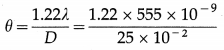
= 2.708 × 10^-6 rad
This is the required angular separation.

Question 86.
Huygens’ wave theory could not explain
(A) interference
(B) reflection
(C) photoelectric effect
(D) refraction.
Answer:
(C) photoelectric effect

Question 87.
The wavefront originating from a point source of light at finite distance is a wavefront.
(A) circular
(B) spherical
(C) plane
(D) cylindrical
Answer:
(B) spherical

Question 88.
In an isotropic medium, the secondary wavelets centred on every point of a given wavefront are all
(A) spherical
(B) cylindrical
(C) oval
(D) of arbitrary shape.
Answer:
(A) spherical

Question 89.
Consider a medium through which light is propagating with a speed v. Given a wavefront, in order to determine the wavefront after a time interval ∆t, the secondary wavelets are drawn with
a radius.
(A) of unit length
(B) v ∆ t
(C) \(\frac{\Delta t}{v}\)
(D) \(\frac{v}{\Delta t}\)
Answer:
(B) v ∆ t

Question 90.
Two points, equidistant from a point source of light, are situated at diametrically opposite positions in an isotropic medium. The phase difference between the light waves passing through the two points is
(A) zero
(B) π/2 rad
(C) π rad
(D) finite, but not these.
Answer:
(A) zero

Question 91.
Wavenormals to spherical wavefronts can be
(A) only diverging
(B) only converging
(C) parallel to each other
(D) diverging or converging.
Answer:
(D) diverging or converging.

Question 92.
Huygens’ principle is used to
(A) obtain the new position of wavefront geometrically
(B) explain the principle of superposition of waves
(C) explain the phenomenon of interference
(D) explain the phenomenon of polarization.
Answer:
(A) obtain the new position of wavefront geometrically

Question 93.
When a ray of light enters into water from air,
(A) its wavelength decreases
(B) its wavelength increases
(C) its frequency increases
(D) its frequency decreases.
Answer:
(A) its wavelength decreases

Question 94.
A parallel beam of light travelling in water is incident obliquely on a glass surface. After refraction, its width
(A) decreases
(B) increases
(C) remains the same
(D) becomes zero.
Answer:
(B) increases

Question 95.
Light of a certain colour has 1800 waves to the millimetre in air. What is its frequency in water?
[n = \(\frac{4}{3}\) for water]
(A) 1.67 × 10⁶ Hz
(B) 4.05 × 10¹⁴ Hz
(C) 5.4 × 10¹⁴ Hz
(D) 7.2 × 10¹⁴ Hz.
Answer:
(C) 5.4 × 10¹⁴ Hz

Question 96.
A ray of light, in passing from vacuum into a medium of refractive index n, suffers a deviation d equal to half the angle of incidence. Then, the refractive index is
(A) sin δ
(B) 2 sin δ
(C) cos δ
(D) 2 cos δ.
Answer:
(D) 2 cos δ.

Question 97.
A ray of light passes from vacuum to a medium of refractive index n. The angle of incidence is found to be twice the angle of refraction. The angle of incidence is
(A) cos^-1 \(\left(\frac{n}{2}\right)\)
(B) cos^-1 (n)
(C) 2cos^-1 \(\left(\frac{n}{2}\right)\)
(D) 2sin^-1 \(\left(\frac{n}{2}\right)\).
Answer:
(C) 2cos^-1 \(\left(\frac{n}{2}\right)\)

Question 98.
If the polarizing angle for a given medium is 60°, then the refractive index of the medium is
(A) \(\frac{1}{\sqrt{3}}\)
(B) \(\frac{\sqrt{3}}{2}\)
(C) 1
(D) \(\sqrt{3}\)
Answer:
(D) \(\sqrt{3}\)

Question 99.
A narrow beam of light in air is incident on glass at an angle of incidence of 58°. If the reflected beam is completely plane polarized, the refractive index of the glass is
(A) 1.9
(B) 1.8
(C) 1.7
(D) 1.6.
Answer:
(D) 1.6.

Question 100.
Polarization of light CANNOT be produced by
(A) reflection
(B) double refraction
(C) dichroism
(D) diffraction.
Answer:
(D) diffraction.

Question 101.
A glass plate of refractive index 1.732 is to be used as a polarizer. Its polarizing angle is
(A) 30°
(B) 45°
(C) 60°
(D) 90°.
Answer:
(C) 60°

Question 102.
Light transmitted through a Polaroid P₁ has an intensity I and is incident on a crossed Polaroid P₂. The intensity of the light transmitted by P₂ is
(A) zero
(B) \(\frac{1}{2}\)I
(C) I
(D) 2I.
Answer:
(A) zero

Question 103.
At points of constructive interference with maximum intensity of two coherent monochromatic waves (wavelength λ), the path difference between them is
(A) zero or an integral multiple of λ
(B) zero or an integral multiple of λ/2
(C) zero or an even integral multiple of λ/2
(D) an odd integral multiple of λ/2.
Answer:
(A) zero or an integral multiple of λ

Question 104.
Two sources of light are said to be coherent if light from them have
(A) the same speed and the same phase
(B) the same phase and the same or nearly the same amplitude
(C) constant phase difference and nearly the same frequency
(D) zero, or some constant, phase difference.
Answer:
(D) zero, or some constant, phase difference.

Question 105.
In a two-source interference pattern, the phase difference between the waves reaching a dark point in radian is (m = 1, 2, 3, …)
(A) 0
(B) mπ
(C) (2m – 1)\(\frac{\pi}{2}\)
(D) (2m – 1)π
Answer:
(D) (2m – 1)π

Question 106.
For destructive interference, the phase difference (in radian) between the two waves should be
(A) 0, 2π, π, …
(B) 0, 2π, 4π, …
(C) π, 3π, 5π, …
(D) \(\frac{\pi}{2}\), \(\frac{3 \pi}{2}\), \(\frac{5 \pi}{2}\), …..
Answer:
(C) π, 3π, 5π, …

Question 107.
For constructive interference, the phase difference (in radian) between the two waves should be
(A) 0, \(\frac{\pi}{2}\), π, …
(B) 0, 2π, 4π, …
(C) π, 3π, 5π, …
(D) \(\frac{\pi}{4}\), \(\frac{\pi}{2}\), \(\frac{3 \pi}{4}\), …..
Answer:
(B) 0, 2π, 4π, …

Question 108.
If λ is the wavelength of light used in Young’s double-slit experiment, the path difference for a phase difference of 11π rad is
(A) 23 λ
(B) 11 λ
(C) 11\(\frac{\lambda}{2}\)
(D) 23\(\frac{\lambda}{2}\)
Answer:
(C) 11\(\frac{\lambda}{2}\)

Question 109.
The fringe width in an interference pattern is W. The distance between the 6th dark fringe and the 4th bright fringe on the same side of the central bright fringe is
(A) 1.5 W
(B) 2 W
(C) 2.5 W
(D) 10.5 W.
Answer:
(A) 1.5 W

Question 110.
Which of the following graphs shows the variation of the fringe width with the frequency of light in a two-source interference pattern ?

Answer:

Question 111.
In an interference pattern using two coherent sources of light, the fringe width is
(A) directly proportional to the wavelength
(B) inversely proportional to the square of the wavelength
(C) inversely proportional to the wavelength
(D) directly proportional to the square of the wavelength.
Answer:
(A) directly proportional to the wavelength

Question 112.
Two slits, 2 mm apart, are placed 300 cm from a screen. When light of wavelength 6000 Å is used, the separation (in mm) between the successive bright lines of the interference pattern is
(A) 0.9
(B) 4.5
(C) 6
(D) 9.
Answer:
(A) 0.9

Question 113.
In two separate setups of Young’s double-slit experiment, the wavelengths of the lights used are in the ratio 1 : 2 while the separation between the slits are in the ratio 2 : 1. If the fringe widths are equal, the ratio of the distances between the slit and the screen is
(A) 1 : 4
(B) 1 : 2
(C) 2 : 1
(D) 4 : 1.
Answer:
(D) 4 : 1.

Question 114.
In Young’s double-slit experiment, the slit separation is reduced to half while the distance of the screen from the slits is increased by 50%. In terms of the initial fringe width, W, the new fringe width is,
(A) \(\frac{1}{4}\) W
(B) \(\frac{3}{4}\) W
(C) \(\frac{3}{2}\) W
(D) 3 W.
Answer:
(D) 3 W.

Question 115.
A pair of slits 1.5 mm apart is illuminated with monochromatic light of wavelength 5500 Å and the interference pattern is obtained on a screen 1.5 m from the slits. The least distance of a point from the central maximum where the intensity is minimum is
(A) 0.275 mm
(B) 0.55 mm
(C) 2.75 mm
(D) 5.5 mm.
Answer:
(A) 0.275 mm

Question 116.
In Young’s double-slit experiment, if a thin transparent sheet covers one of the slits, the optical path of the wave from that slit
(A) increases
(B) decreases
(C) changes by \(\frac{D}{d}\) (n_m – 1)t
(D) is not affected.
Answer:
(A) increases

Question 117.
In Young’s double-slit experiment, if a thin mica sheet of thickness t and refractive index n_m covers one of the slits, the optical path of the wave from that slit
(A) increases by (n_m – 1 )t
(B) decreases by (n_m – 1) t
(C) changes by \(\frac{D}{d}\) (n_m – 1) t
(D) is not affected.
Answer:
(A) increases by (n_m – 1 )t

Question 118.
In a two-slit intereference experiment, if a thin transparent sheet of thickness f and refractive index n_m covers both the slits, the optical path difference between the two interfering waves
(A) increases by (n_m – 1)t
(B) decreases by (n_m – 1)t
(C) changes by \(\frac{D}{d}\)(n_m – 1)t
(D) is not affected.
Answer:
(D) is not affected.

Question 119.
In a biprism experiment two interfering waves are produced by division of
(A) amplitude
(B) wavefront
(C) amplitude and wavefront
(D) neither wavefront nor amplitude.
Answer:
(B) wavefront

Question 120.
In Fresnel’s biprism experiment, with the eyepiece 1 m from the two coherent sources, the fringe width obtained is 0.4 mm. If just the eyepiece is moved towards the biprism by 25 cm, then the fringe width
(A) decreases by 0.01 mm
(B) decreases by 0.1 mm
(C) increases by 0.01 mm
(D) increases by 0.1 mm.
Answer:
(B) decreases by 0.1 mm

Question 121.
In a biprism experiment, keeping the experimental setup unchanged, the fringe width
(A) increases with increase in wavelength
(B) decreases with increase in wavelength
(C) increases with decrease in wavelength
(D) remains unchanged with change in wavelength.
Answer:
(A) increases with increase in wavelength

Question 122.
In finding the distance between the two coherent sources in Fresnel’s biprism experiment by the conjugate foci method, one uses
(A) a long focus convex lens that forms real images of the virtual sources
(B) a short focus concave lens that forms real images of the virtual sources
(C) a short focus convex lens that forms virtual images of the virtual sources
(D) a short focus convex lens that forms real images of the virtual sources.
Answer:
(D) a short focus convex lens that forms real images of the virtual sources.

Question 123.
Using a light of wavelength 4800 Å in Fresnel’s biprism experiment, 21 fringes are obtained in a given region. If light of wavelength 5600 Å is used, the number of fringes in the same region will be
(A) 14
(B) 18
(C) 21
(D) 24.
Answer:
(B) 18

Question 124.
To obtain pronounced diffraction with a single slit illuminated by light of wavelength λ, the slit width should be
(A) of the same order as λ
(B) considerably larger than λ
(C) considerably smaller than λ
(D) exactly equal to λ/2.
Answer:
(B) considerably larger than λ

Question 125.
In single-slit diffraction, which of the following are equal ?
(A) Widths of all bright and dark fringes
(B) Intensities of non-central bright fringes
(C) Widths of non-central bright fringes
(D) Both widths and intensities of noncentral bright fringes.
Answer:
(C) Widths of non-central bright fringes

Question 126.
In single slit diffraction (at a narrow slit of width a), the intensity of the central maximum is
(A) independent of a
(B) proportional to a
(C) proportional to a²
(D) inversely proportional to a.
Answer:
(D) inversely proportional to a.

Question 127.
For a single slit of width a, the diffraction pattern minima are located at angles θ_m, where m is a positive, non-zero integer. Which of the following expressions is most correct ?
(A) a sin θ_m = mλ
(B) a sin θ_m = \(\frac{m \lambda}{2}\)
(C) a sin θ_m = (2m + 1)\(\frac{\lambda}{2}\)
(D) a sin θ_m = (2m – 1)\(\frac{\lambda}{2}\)
Answer:
(A) a sin θ_m = mλ

Question 128.
In a diffraction pattern due to a single slit of width a with incident light of wavelength λ, at an angle of diffraction θ, the condition for the first minimum is
(A) λ sin θ = a
(B) a cos θ = λ
(C) a sin θ = λ
(D) λ cos θ = a.
Answer:
(C) a sin θ = λ

Question 129.
The fringes produced in a diffraction pattern are of
(A) equal width with the same intensity
(B) unequal width with varying intensity
(C) equal intensity
(D) equal width with varying intensity.
Answer:
(B) unequal width with varying intensity

Question 130.
For a single slit of width a, the first diffraction maximum with light of wavelength λ subtends an angle θ such that sin θ is equal to
(A) \(\frac{\lambda}{2 a}\)
(B) \(\frac{\lambda}{a}\)
(C) \(\frac{1.5 \lambda}{a}\)
(D) \(\frac{2 \lambda}{a} .\)
Answer:
(C) \(\frac{1.5 \lambda}{a}\)

Question 131.
Fraunhofer diffraction pattern of a parallel beam of light (wavelength λ) passing through a narrow slit (width a) is observed on a screen using a convex lens (focal length f). The angular half-width of the central fringe is
(A) \(\frac{2 \lambda f}{a}\)
(B) \(\frac{\lambda f}{a}\)
(C) \(\frac{2 \lambda}{a}\)
(D) \(\frac{\lambda}{a}\)
Answer:
(D) \(\frac{\lambda}{a}\)

Question 132.
A parallel beam of light (λ = 5000 Å) is incident normally on a narrow slit of width 0.2 mm. The angular separation between the first two minima is
(A) 2.5 × 10^-3 degree
(B) 2.5 × 10^-3 rad
(C) 5 × 10^-3 degree
(D) 5 × 10^-3 rad.
Answer:
(B) 2.5 × 10^-3 rad

Question 133.
A parallel beam of light (λ = 5000 Å) is incident normally on a narrow slit of width 0.2 mm. The Fraunhofer diffraction pattern is observed on a screen placed at the focal plane of a convex lens (f = 20 cm). The first two minima are separated by
(A) 0.005 cm
(B) 0.05 cm
(C) 2.5 mm
(D) 5 mm.
Answer:
(B) 0.05 cm

Question 134.
A plane wave of wavelength 5500 Å is incident normally on a slit of width 2 × 10^-2 cm. The width of the central maximum on a screen 50 cm away is
(A) 2.50 × 10^-3 cm
(B) 2.75 × 10^-3 cm
(C) 2.75 × 10^-3 m
(D) 5.50 × 10^-3 m.
Answer:
(D) 5.50 × 10^-3 m.

Question 135.
If NA is the numerical aperture of a microscope objective, then its resolving power with an illumination of wavelength λ is
(A) \(\frac{0.5 \lambda}{\mathrm{NA}}\)
(B) \(\frac{0.61 \lambda}{\mathrm{NA}}\)
(C) \(\frac{1.22 \mathrm{NA}}{\lambda}\)
(D) \(\frac{2 \mathrm{NA}}{\lambda}\)
Answer:
(A) \(\frac{0.5 \lambda}{\mathrm{NA}}\)

Question 136.
A microscope with numerical aperture 0.122 is used with light of wavelength 6000 A. The limit of resolution is
(A) 3.33 × 10⁶ m
(B) 3.33 mm
(C) 3 × 10^-6 m
(D) 3 × 10^-7 m.
Answer:
(C) 3 × 10^-6 m

Question 137.
The objective lens of a telescope has a diameter D. The angular limit of resolution of the telescope for light of wavelength λ is
(A) \(\frac{D}{1.22 \lambda}\)
(B) \(\frac{1.22 \lambda}{D}\)
(C) \(\frac{D}{0.61 \lambda}\)
(D) \(\frac{0.61 \lambda}{D} .\)
Answer:
(B) \(\frac{1.22 \lambda}{D}\)

Question 138.
Two closely-spaced distant stars are just resolved when seen through a telescope with an objective lens of diameter D and focal length f. The separation between their images is given by.
(A) \(\frac{D}{1.22 \lambda f}\)
(B) \(\frac{f \mathcal{D}}{1.22 \lambda}\)
(C) \(\frac{1.22 \lambda f}{D}\)
(D) \(\frac{1.22 D \lambda}{f}\)
Answer:
(C) \(\frac{1.22 \lambda f}{D}\)

Question 139.
High magnifying power microscopes have oil-immersion objectives
(A) to increase the fringe width
(B) to increase the numerical aperture of the objective
(C) to decrease the wavelength of light
(D) because oil does not damage the observed sample.
Answer:
(B) to increase the numerical aperture of the objective

Question 140.
If the numerical aperture of a microscope is increased, then its
(A) resolving power decreases
(B) limit of resolution decreases
(C) resolving power remains constant
(D) limit of resolution increases
Answer:
(B) limit of resolution decreases

Question 141.
The numerical aperture of the objective of a microscope is 0.12. The limit of resolution, when light of wavelength 6000 A is used to view an object, is
(A) 0.25 × 10^-7 m
(B) 2.5 × 10^-7m
(C) 25 × 10^-7 m
(D) 250 × 10^-7 m.
Answer:
(C) 25 × 10^-7 m

Question 142.
The resolving power of a refracting telescope is increased by
(A) using oil-immersion objective
(B) increasing the diameter D of the objective lens
(C) resorting to short-wavelength radiation
(D) increasing D and using smaller λ.
Answer:
(D) increasing D and using smaller λ.

Question 143.
The resolving power of a telescope of aperture 100 cm, for light of wavelength 5.5 × 10^-7 m, is
(A) 0.149 × 10⁷
(B) 1.49 × 10⁷
(C) 14.9 × 10⁷
(D) 149 × 10⁷
Answer:
(A) 0.149 × 10⁷

Question 144.
The resolving power of a telescope depends upon the
(A) length of the telescope
(B) focal length of the objective
(C) diameter of the objective
(D) focal length of the eyepiece.
Answer:
(C) diameter of the objective

Question 145.
If a is the aperture of a telescope and 2 is the wavelength of light then the resolving power of the telescope is
(A) \(\frac{\lambda}{1.22 a}\)
(B) \(\frac{1.22 a}{\lambda}\)
(C) \(\frac{1.22 \lambda}{a}\)
(D) \(\frac{a}{1.22 \lambda}\)
Answer:
(D) \(\frac{a}{1.22 \lambda}\)

Question 146.
Using a monochromatic light of wavelength 2 in Young’s double-slit experiment, the eleventh dark fringe is obtained on the screen for a phase difference of
(A) \(\frac{11}{2}\) π rad
(B) \(\frac{21}{2}\) π rad
(C) 13 π rad
(D) 21 π rad
Answer:
(D) 21 π rad