Balbharti Maharashtra State Board Class 12 Economics Important Questions Chapter 6 Index Numbers Important Questions and Answers.
Maharashtra State Board 12th Economics Important Questions Chapter 6 Index Numbers
1. A. Choose the correct option:
Question 1.
Index Numbers are used –
(a) to determine production
(b) to determine the level of employment
(c) to revise dearness allowance
(d) to revise cost of living
Options :
(1) a, b and c
(2) b, c and d
(3) c and d
(4) only d
Answer:
(3) c and d
![]()
Question 2.
Statements related to features of Index Numbers.
These are specialised form of averages. These help to determine price index.
These are not the barometers of economic activity.
Base year is taken as 100.
Options :
(1) a, b and d
(2) b, c and d
(3) b and c
(4) All of these
Answer:
(1) a, b and d
Question 3.
How does purchasing power changes with the increase in price level?
(a) Remains unchanged
(b) Increases
(c) Decreases
(d) None of these
Options :
(1) a, b and c
(2) b, c and d
(3) only c
(4) only b
Answer:
(3) only c
Question 4.
What do Index numbers measure?
(a) Value of money
(b) Relative prices
(c) Relative change in prices
(d) All of these
Options :
(1) b, c and d
(2) only b
(3) only c
(2) a, b and c
Answer:
(3) only c
(B) Complete the Correlation.
- Base year quantity : …………….. :: Current year quantity : 125
- Present period : Current period :: Past period : ……………..
- All commodities with equal importance : …………….. :: All commodities with different importance :: Weighted Index
- Dearness Allowance : Consumer Price Index :: Standard of Living : ……………..
- P01 = \(\frac{\Sigma p_{1} q_{0}}{\Sigma p_{0} q_{0}}\) x 100 : Laspeyre’s Index ::
P01 = \(\frac{\Sigma p_{1} q_{1}}{\Sigma p_{0} q_{1}}\) x 100 = ……………..
Answers:
- 100
- Base period
- Simple Index
- Cost of Living Index
- Paasche’s Index
![]()
(C) Give economic terms.
(1) Index number calculated from a single variate.
(2) Index number calculated from a group of variable.
(3) The year for which Index number is being prepared.
(4) The year from which the changes are measured.
(5) Barometer of economic activity.
(6) Index which measures price level of goods traded in whole sale market.
(7) Average of quantity of commodities produced in different sectors of the economy.
(8) Index which measures price level of goods in retail market.
(9) Base year index number.
(10) Purchasing power of money is measured by.
(11) Quantity Index number is also called.
(12) Index which helps in determining the depreciation cost of durable goods.
(13) Base year is also known as.
(14) Laspeyre uses period quantity as weights.
(15) Paasche uses period quantity as weights.
Answer:
(1) Unvariate index
(2) Composite index
(3) Current year
(4) Base year
(5) Index numbers
(6) Wholesale Price index
(7) Quantity Index number
(8) Retail Price Index number
(9) 100
(10) Cost of Living Index
(11) Volume Index number
(12) Price Index
(13) Reference year
(14) Base
(15) Current
(D) Complete the following sentences.
(1) Index numbers are ………….. averages.
(2) Index number is an ………….. barometer.
(3) A base year should be a………….. year.
(4) The ratio of current year price to the base year price multiplied by 100 is called ………….. index number.
(5) ………….. index number is the average of all quantity of commodities produced in different sectors.
(6) ………….. index number is a simple average of the index numbers of individual goods.
(7) ………….. Index number gives equal importance to all items.
(8) Purchasing power of money can be measured by………….. index number.
(9) To know the changes in production………….. index number is more useful.
(10) Index number for the base year is …………..
(11) ………….. refer to the relative importance of different items in the construction of Index Number.
Answers:
- specialised
- economic
- recent
- Price
- Quantity
- Simple
- Simple
- cost of living
- quantity
- 100
- Weights
![]()
(E) Choose the correct pair :
I.
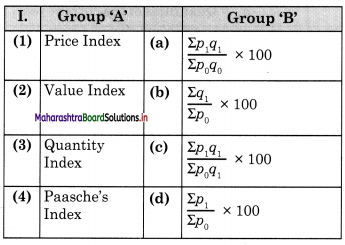
Answer:
Options :
(1) (1) – d, (2) – c, (3) – a, (4) – b
(2) (1) – d, (2) – a, (3) – b, (4) – c
(3) (1) – b, (2) – c, (3) – d, (4) – a
(4) (1) – c, (2) – d, (3) – a, (4) – b
Answer:
(2) (1) – d, (2) – a, (3) – b, (4) – c
II.
| Group ‘A’ | Group ‘B’ |
| (1) Index Number | (a) Cost of living |
| (2) Dearness Allowance | (b) Economic Barometer |
| (3) Base year | (c) Wholesale Price Index |
| (4) Whole sale market goods | (d) 100 |
Options :
(1) (1) – b, (2) – a, (3) – d, (4) – c
(2) (1)- c, (2) – d, (3)- a, (4) – b
(3) (1)- d, (2) c, (3)- b, (4) – a
(4) (1)- a, (2) b, (3) c, (4) – d
Answer:
(1) (1) – b, (2) – a, (3) – d, (4) – c
2. Answer the following :
Question 1.
What are the different methods of constructing Index numbers?
Answer:
Following chart helps to know different methods of constructing Index Numbers:

(A) Simple Index Number : A Simple Index Number is constructed when all the items like food, clothing, transport, housing, etc. are given equal importance. There are three methods of constructing it.
1. Price Index Number : It is calculated using the following formula:
P01 = \(\frac{\Sigma p_{1}}{\Sigma p_{0}}\) x 100
where – P01 = Price Index Number
Σp1 = Total of the current year price of various commodities.
Σp0 = Total of base year prices of various commodities.
2. Quantity Index Number : It is calculated by using the following formula :
Quality Index Number Q01 = \(\frac{\Sigma q_{1}}{\Sigma q_{0}}\) x 100
where, Σq1 = Sum total of current year quantities of all commodities
Σq0 = Sum total of base year quantities of all commodities
3. Value Index Number : It is calculated by using the following formula:
Value Index Number V01 = \(\frac{\Sigma p_{1} q_{1}}{\Sigma p_{0} q_{0}}\) x 100
where, Σp1q1 = Sum total of the product of the prices and quantities of the current year
Σp0q0 = Sum total of the product of the prices and quantities of the base year.
![]()
(B) Weighted Index Number : Under this method, physical quantities are used as weights, therefore prices themselves are weighted by quantities. We can take either the base year quantities or current year quantities as weights or the average of the two.
These index numbers are the simple aggregative type with the fundamental difference that weights are assigned to the various items included in the index.
There are two methods of constructing it.
(1) Laspeyre’s Method
(2) Paasche’s Method
(1) Laspeyre’s Method : This method was devised by Laspeyre’s, a German economist in 1871. In this method the weights are determined by quantities in the base year.
P01 = \(\frac{\Sigma p_{1} q_{0}}{\Sigma p_{0} q_{0}}\) x 100
where, P01 = Price Index Number.
p0 = Prices of the base year.
q0 = Quantities of the base year,
p1 = Prices of the current year.
Σ p1q0 = Sum of all the products of p, and q0.
Σ p0q0 = Sum of all the products of p0 and q0.
(2) Paasche’s Method : This method was devised by a German economist known as Hermann Paasche in 1874. The weights of current year are used as base year in constructing the Index Number.
P01 = \(\frac{\Sigma p_{1} q_{1}}{\Sigma p_{0} q_{1}}\) x 100
where, P01 = Price Index Number.
p1 = Prices of the current year.
q1 = Quantities of the current year.
p0 = Prices of the base year.
Σp1q1 = Sum of all the products of p1 and q1,
Σp0q1 = Sum of all the products of p0 and q1
Question 2.
Explain the features of Index Numbers. ?
Answer:
Features of Index Numbers :
- Index numbers are a specialised form of averages.
- They are expressed in percentage form without using a percentage sign.
- The year for which index number is being prepared is the current year.
- The year from which index number is being prepared is called the base year which is always taken as 100.
- They are used in measuring the changes in magnitudes which cannot be measured directly.
- The formula used for Price Index Number = \(\frac { Total price of the current year }{ Total price of the base year }\) x 100
- They are considered as barometer of economic activity.
- Index number which is calculated from a single variable is called “univariate • index” and which is constructed from a group of variables is called a “composite index”.
Question 3.
Explain the steps involved in the construction of index numbers.
Answer:
Steps involved in the construction of index numbers are as follows :
- Purpose of an Index Number : Before constructing an index number, one must know the purpose for which the index number is constructed. E.g. for the whole c sale price or retail price or for agricultural output, etc.
- Selection of a Base Year : It is important to select a base year against which comparisons are made. So base year or reference year should be a recent year and not a distant past. it should be normal and free from natural calamities, war, etc.
- Selection of Commodities: When the cost c of living index number of the middle class families is to be constructed, the items that are used by middle class families in everyday life should be included and items like big cars, AC’s, etc. should not be included.
- Selection of Prices : Prices differ from city ‘I to city and even from shop to shop in the same city. Hence, we should take a few standard shops from where middle class families buy goods and take the average of the prices of goods sold by them. Otherwise index number constructed may be misleading.
- Selection of suitable Average : An ; index number is a special kind of average, Generally arithmetic mean is commonly ? used for construction of index number as it is simple to calculate.
- Selection of Formula : Number of formulae can be used for construction, of index numbers. Economists have to decide which formula to use for the construction of a particular index number.
- Assigning proper Weights : Weights refer to the relative importance of different items in the construction of an index number. Weights may either be quantity weights (q) or value weights (p). All weights may not be equally important. Therefore, by s assigning specific weights better result can be obtained.
3. State with reasons whether you agree or disagree with the following statements:
Question 1.
Index Numbers can be constructed without the base year.
Answer:
No, I do not agree with this statement.
Index numbers can be constructed without the base year because :
- Index Numbers are the tools for measuring the changes in the magnitude of a variable or a group of variables over time with respect to a chosen year.
- Prices of some goods may increase and of other may decrease during the two periods. Index numbers solves this problem by taking the average change.
- For example, to know cost of living of people in general in India, Government chooses a base year 2010 which is taken as 100. Then cost of living is calculated in 2019 which may be 140.
- This difference of 40(140-100) shows that cost of living in India has increased by 40% since 2010.
Hence, Index Numbers cannot be constructed – without the base year.
![]()
Question 2.
Any year can be taken as a base year for index number.
Answer:
No, I do not agree with this statement.
- In preparing index number the first step is c to select a year which serves as a reference)period.
- The prices in any other year are compared to the prices in the base year.
- The base year should be a recent year.
- If the base year is in the distant past, the result will not be meaningful. E.g. if the index number of the cost of living is calculated for the current year and compared with adistant past of 1970 as a base year it will not be meaningful.
- Base year should also be a year when the prices are regarded as normal prices.
Hence, any year cannot be taken as a base year for index number.
Question 3.
Index numbers are very useful in economics and business.
OR
Index numbers are economic barometer.
Answer:
Yes, I do agree with this statement. Index numbers are very useful in economics and business and are used as powerful tools to measure the changes in various phenomena over a period of time like; measuring changes in the cost of living, wholesale prices, industrial production, exports, etc.
Uses of Index Numbers are :
- They help in the study of trends.
- They act as an economic barometer.
- They measure the purchasing power of money.
- They help to adjust national income.
- They provide guidelines for formulating policies and arriving at decisions.
Hence, Index numbers are very useful in economics and business.
4. Answer in detail
Question 1.
Define index number. What are its main features?
Answer:
(A) Definition:
Different economists define index numbers in different ways.
- According to Spiegel, index number is, “a statistical measure to show changes in variable or a group of related variables with reference to time, geographical location and other characteristics such as income, profession, etc.”
- Croxton and Cowden defines index numbers as, “a device for measuring difference in the magnitude of a group of related variables.”
- According to Bewley, “Index Numbers are used to measure the changes in some quantity which cannot be observed directly. ”
(B) Meaning:
An index number is a specialised average which measures percentage changes in a variable (or a group of variables) over a specified time. When we say that the index of the whole sale price for the year 2018 is 125, taking the base year as 2015, it means that there is an increase of the wholesale price by 25%. Hence, index numbers are used to measure general changes in price, cost of living, wages, production, stock market, etc. Therefore, they are called “economic barometer”.
(C) Features of Index Numbers :
- Index numbers are a specialised form of averages.
- They are expressed in percentage form without using a percentage sign.
- The year for which index number is being prepared is the current year.
- The year from which index number is being prepared is called the base year which is always taken as 100.
- They are used in measuring the changes in magnitudes which cannot be measured directly.
- The formula used for Price Index Number = \(\frac { Total price of the current year }{ Total price of the base year }\) x 100
- They are considered as barometer of economic activity.
- Index number which is calculated from a single variable is called “univariate • index” and which is constructed from a group of variables is called a “composite index”.
Question 2.
What are the different types of Index Numbers?
Answer:
Index numbers may be of following types.
(A) Price Index Number It may be further classified into:
- Retail Price Index Number
- Wholesale Price Index Number
- Cost of Living Index Number
(B) Quantity Index Number
(C) Special Purpose Index Number
(D) Value Index Number
(A) Price Index Number : A price index number measures the changes in the prices of an entire group of related commodities over a period of time. It may be of following three types.
(i) Retail Price Index Number : These are ; complied to measure the changes in the retail price of various commodities eg. index number of consumer prices, bonds, etc.
(ii) Wholesale Price Index Number : This measures price level of goods traded in the wholesale market. They indicate general changes in the purchasing power of money.
(iii) Cost of Living Index Number: It is special type of retail price index which shows the price variations in a group of commodities consumed by different classes of people over a period of time. This index number aims ‘ to measure the changes in cost of living of different classes of people over a period of time e.g. cost of living index number of middle class people, rich class people, etc.
(B) Quantity Index Number: It is the average of the quantity of commodities produced in different sectors of the economy. It helps us to know whether the level of production in the country is rising or falling as compared to the production in previous years. It is also called volume index number.
(C) Special Purpose Index Number : Special purpose index numbers are constructed to know the index of productivity of labour, exports and imports, shares on stock market, etc.
(D) Value Index Number : It measures the relative changes in the total value of items like retail sales, profit, etc. as compared to their level in the base year. It is obtained by multiplying the price of an item with its quantity (P x Q).
![]()
Question 3.
Explain the significance / uses of index numbers in economics?
Answer:
Index numbers are significant tools of economic analysis in the following ways:
(1) Help in formulating Policies : Index numbers help the government and business organisations in framing their suitable economic policies for agriculture and industrial sector, wage and dearness allowance policies, etc.
(2) Help in the study of Trends and Tendencies : Index numbers study the relative changes in the level of phenomenon of different periods of time, so they can be used to predict future events. The economists can study the general trends of changes in price levels, agricultural and industrial production, export, imports, etc.
(3) Economic Barometer : Just as barometer is used to measure atmospheric pressure, index numbers measure the level of economic and business behaviour. They are very important for an economist, businessman, planners, policy makers, etc.
(4) Helps in Measurement of Inflation :
It helps the government to take measures against inflation by giving additional D.A. to the employees on the basis of Dearness Index.
(5) Help to adjust National Income : By comparing current year’s national product prices with the base year’s prices, the Domestic Product (GDP) produced. Hence, this shows changes in real national income.
(6) To present Financial Data in Real Income : Index numbers are used to adjust price change, wage change, etc. Thus deflating helps to present the financial data at constant prices.
(Note: Deflating means to make adj ustments / in the original data)
(7) Helps in determining Depreciation Cost: The price index helps in determining the depreciation cost of durable goods. At the time of inflation, it is useful to know the ) original cost of the commodities.
Question 4.
What are the limitation of Index Numbers?
Answer:
Although index numbers are very useful to business and industry, they suffer from the ) following limitations: ;
(1) Bias in the Data : Index numbers are constructed on the basis of various types of data. If the data is not collected properly, we may not get proper index numbers.
(2) Misuse of Index Numbers: Index numbers can be misused. We compare the index numbers with the base year. Hence a person may choose a base year which is suitable forhis purpose. A businessman may use a base year in which profits are high and show that his profits are falling now.
(3) Based on Samples : Index numbers are based on samples so it cannot include all the items in the consideration of index numbers. Hence index numbers are not free from sampling errors.
(4) Defects in the Formulae : There are number of formulae, but every formula suffers from some defects. Index number is an average , so index number may have the same limitations which an average may have.
(5) Changes in the Economy : In the long run, habits, tastes and expectations of people change, so it is difficult to incorporate all these changes in index numbers. For a good index number items should remain the same price wise over a period of time. But this is practically not possible.
(6) Neglecting Qualitative Change : The index number of price (or) production (or) quantity may ignore the change in quality of the commodities which may be significant at any point of time. A better quality commodity will cost more than an inferior commodity. So a rise in the price index may be due to an improvement in the quality and not due to a rise in prices.
(7) Arbitrary Weights : The weights (relative importance) assigned to different commodities may be random.
(8) Limited Scope : An index number is useful for the purpose for which it is designed. So its use is limited only to that phenomenon and not for another purpose.
5. Solved Examples Construction of Index Numbers
Question 1.
Calculate the price index number based for the following data.
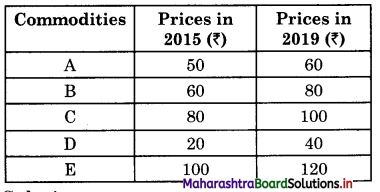
Solution:
Calculate the price index number
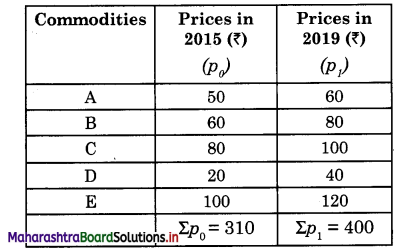
where, P01 = Price Index
Σp1 = Sum total of current year prices of all commodities
Σp0 = Sum total of base year prices of all commodities
p01 = \(\frac{\Sigma p_{1}}{\Sigma p_{0}}\) x 100
= \(=\frac{400}{310}\) x 100
= 129.03 g
Hence, P01 = 129.03 g
![]()
Question 2.
Calculate a Quantity Index number of g the given data.
Solution :
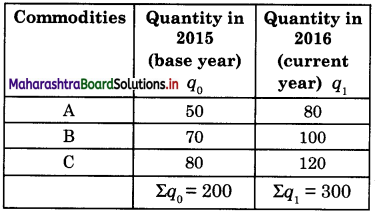
where, Σq0 = Sum total of all the commodities of the base year
Σq1 Sum total of all the commodities of the current year
Quantity Index Number Q01 = \(\frac{\Sigma q_{1}}{\Sigma q_{0}}\) x 100
= \(\frac{300}{200}\) x 100
= 150
Hence, Q01 = 150
Question 3.
Calculate Value Index number using a simple method of the following data:
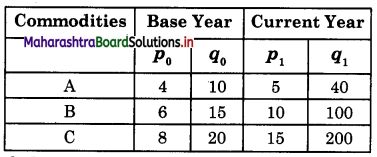
Solution:
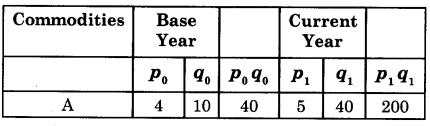
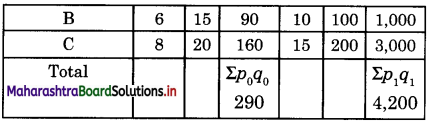
Steps : Σp0q0 = Sum total of product of the p0 and q0 of base year
Σp1q1 = Sum total of product of the p1 and q1 of current year
Value Index Number V01 = \(\frac{\Sigma p_{1} q_{1}}{\Sigma p_{0} q_{0}}\) x 100
= \(\frac{4,200}{290}\) x 100
= 1,448
Hence, V01 = 1,448
Question 4.
Given below are the price quantity data with price quoted in Rs. per kg and production in quintals. Construct index number by Laspeyre’s method.
Solution:
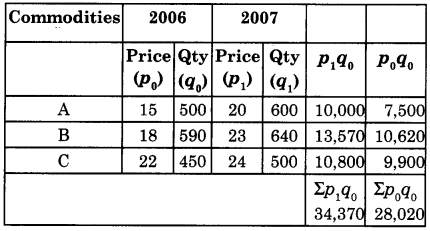
Steps: Σp1q0 = Sum total of product p1 and q0
Σp0q0 = Sum total of product p0 and q0
P01 = \(\frac{\Sigma p_{1} q_{0}}{\Sigma p_{0} q_{0}}\) x 100
= \(\frac{34,370}{28,020}\) x 100
= 122.66
Hence P01 = 122.66
![]()
Question 5.
Construct the index number by Paasche’s method.
Solution :
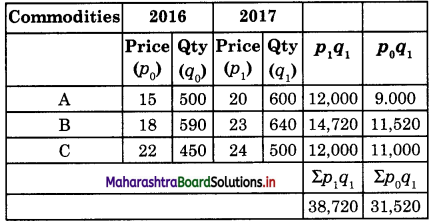
Steps : Σp1q1 = Sum total of product of the P1 and q1
Σp1q1= Sum total of product P0 and q1
p01 = \(\frac{\Sigma p_{1} q_{1}}{\Sigma p_{0} q_{1}}\) x 100
= \(\frac{38,720}{31,520}\) x 100
= 122.84
Hence P01 = 122.84
Question 6.
Calculate Laspeyre’s and Paasche’s Index from the given data.
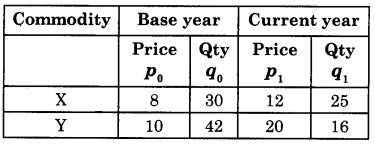
Answer:
(A) Calculation of Laspeyre’s Index Number:
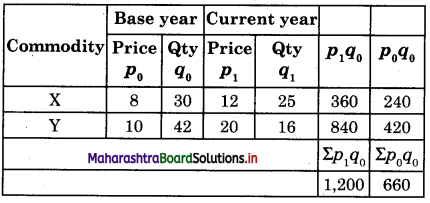
Laspeyre’s Index P01 = \(\frac{\Sigma p_{1} q_{0}}{\Sigma p_{0} q_{0}}\) x 100
= \(\frac{1,200}{660}\) x 100
= 181.81
![]()
(B) Paasche’s Index Number :
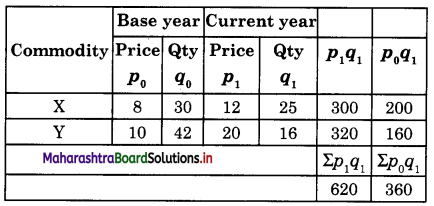
Paasche’s Index Number
P01 = \(\) x 100
= \(\) x 100
= 172.22
Laspeyre’s Index = 181.81
Paasche’s Index = 172.22
Question 7.
Construct Price Index Number from the given data.
Answer:
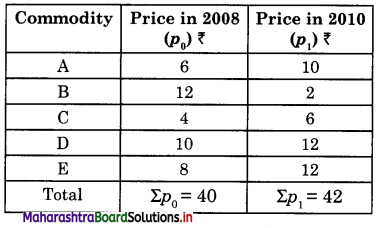
Price Index P01 = \(\) x 100
= \(\frac{42}{40}\) x 100
= 105
Hence, P01 = 105
Question 8.
Construct Value Index Number of the following data.
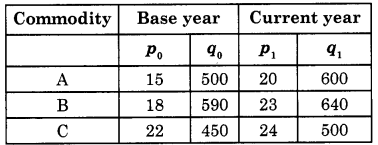
Answer:
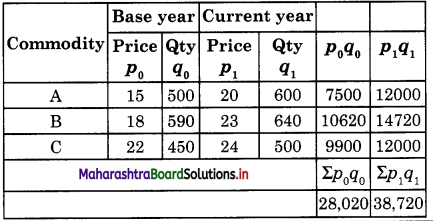
V01 = \(\) x 100
= \(\) x 100
= 138.18
Hence V01 = 138.18
Question 9.
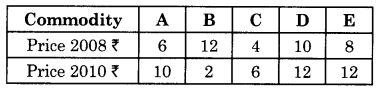
Calculate Laspeyre’s and Paasche’s Price Index numbers from the given data.
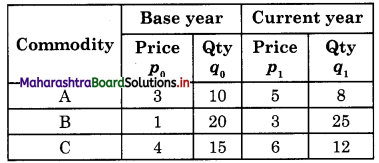
Answer:
Construction of Laspeyre’s and Paasche’s Price index Numbers.
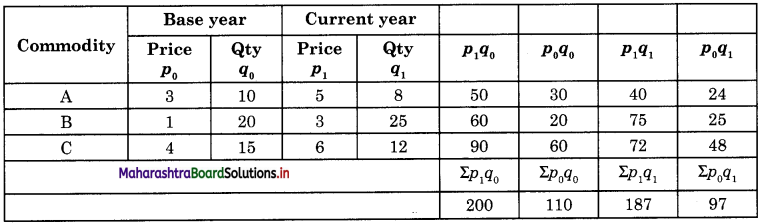
(A) Laspeyre’s Price Index Number:
P01 = \(\frac{\Sigma p_{1} q_{0}}{\Sigma p_{0} q_{0}}\) x 100
= \(\frac{200}{110}\) x 100
= 181.81
![]()
(B) Paasche’s Price Index Number:
P01 = \(\frac{\Sigma p_{1} q_{1}}{\Sigma p_{0} q_{1}}\) x 100
= \(\frac{187}{97}\) x 100
= 192.78
(A) Laspeyre’s P01 = 181.81
(B) Paasche’s P01 = 192.78