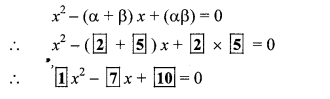Maharashtra Board 10th Class Maths Part 1 Practice Set 2.5 Solutions Chapter 2 Quadratic Equations

Balbharti Maharashtra State Board Class 10 Maths Solutions covers the Practice Set 2.5 Algebra 10th Class Maths Part 1 Answers Solutions Chapter 2 Quadratic Equations.

Practice Set 2.5 Algebra 10th Std Maths Part 1 Answers Chapter 2 Quadratic Equations

Question 1.
Fill in the gaps and complete.

Answer:

Question 2.
Find the value of discriminant.
i. x² + 7x – 1 = 0
ii. 2y² – 5y + 10 = 0
iii. √2 x² + 4x + 2√2 = 0
Solution:
i. x² +7 x – 1 = 0
Comparing the above equation with
ax² + bx + c = 0, we get
a = 1, b = 7, c = -1
∴ b²– 4ac = (7)² – 4 × 1 × (-1)
= 49 + 4
∴ b² – 4ac = 53

ii. 2y² – 5y + 10 = 0
Comparing the above equation with
ay² + by + c = 0, we get
a = 2, b = -5, c = 10
∴ b² – 4ac = (-5)2 -4 × 2 × 10
= 25 – 80
∴ b² – 4ac = -55

iii. √2 x² + 4x + 2√2 = 0
Comparing the above equation with
ax + bx + c = 0, we get
a = √2,b = 4, c = 2√2
∴ b² – 4ac = (4)2 – 4 × √2 × 2√2
= 16 – 16
∴ b² – 4ac =0

Question 3.
Determine the nature of roots of the following quadratic equations.
i. x² – 4x + 4 = 0
ii. 2y² – 7y + 2 = 0
iii. m² + 2m + 9 = 0
Solution:
i. x² – 4x + 4= 0
Comparing the above equation with
ax² + bx + c = 0, we get
a = 1,b = -4, c = 4
∴ ∆ = b² – 4ac
= (- 4)² – 4 × 1 × 4
= 16 – 16
∴ ∆ = 0
∴ Roots of the given quadratic equation are real and equal.

ii. 2y² – 7y + 2 = 0
Comparing the above equation with
ay² + by + c = 0, we get
a = 2, b = -7, c = 2
∴ ∆ = b² – 4ac
= (- 7)² – 4 × 2 × 2
= 49 – 16
∴ ∆ = 33
∴ ∆ > 0
∴ Roots of the given quadratic equation are real and unequal.

iii. m² + 2m + 9 = 0
Comparing the above equation with
am² + bm + c = 0, we get
a = 1,b = 2, c = 9
∴ ∆ = b² – 4ac
= (2)² – 4 × 1 × 9
= 4 – 36
∴ ∆ = -32
∴ ∆ < 0
∴ Roots of the given quadratic equation are not real.

Question 4.
Form the quadratic equation from the roots given below.
i. 0 and 4
ii. 3 and -10
iii. \(\frac { 1 }{ 2 } \) , \(\frac { 1 }{ 2 } \)
iv. 2 – √5, 2 + √5
Solution:
i. Let a = 0 and β = 4
∴ α + β = 0 + 4 = 4
and α × β = 0 × 4 = 0
∴ The required quadratic equation is
x² – (α + β) x + αβ = 0
∴ x² – 4x + 0 = 0
∴ x² – 4x = 0

ii. Let α = 3 and β = -10
∴ α + β = 3 – 10 = -7
and α × β = 3 × -10 = -30
∴ The required quadratic equation is
x² – (α + β)x + αβ = 0
∴ x² – (-7) x + (-30) = 0

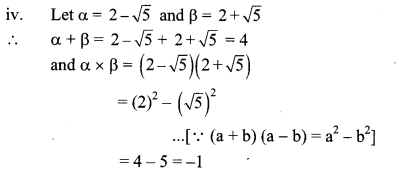
∴ The required quadratic equation is
x² – (α + β)x + αβ = 0
∴ x² – 4x – 1 = 0

Question 5.
Sum of the roots of a quadratic equation is double their product. Find k if equation is x² – 4kx + k + 3 = 0.
Solution:
x² – 4kx + k + 3 = 0
Comparing the above equation with
ax² + bx + c = 0, we get
a = 1, b = – 4k, c = k + 3
Let α and β be the roots of the given quadratic equation.
Then, α + β  = \(\frac { -b }{ a } \) and αβ = \(\frac { c }{ a } \)
According to the given condition,

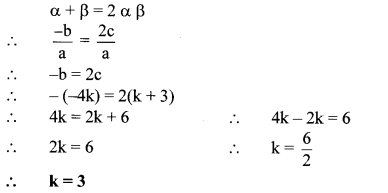
Question 6.
α, β are roots of y² – 2y – 7 = 0 find,
i. α² + β²
ii. α³ + β³
Solution:
y² – 2y – 7 = 0
Comparing the above equation with
ay² + by + c = 0, we get
a = 1, b = -2, c = -7

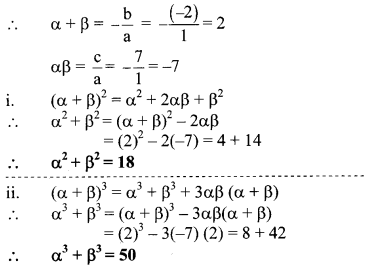
Question 7.
The roots of each of the following quadratic equations are real and equal, find k.
i. 3y² + ky + 12 = 0
ii. kx (x-2) + 6 = 0
Solution:
i. 3y² + kg + 12 = 0
Comparing the above equation with
ay² + by + c = 0, we get
a = 3, b = k, c = 12
∴ ∆ = b² – 4ac
= (k)² – 4 × 3 × 12
= k² – 144 = k² – (12)²
∴ ∆ = (k + 12) (k – 12) …[∵ a² – b² = (a + b) (a – b)]
Since, the roots are real and equal.
∴ ∆ = 0
∴ (k + 12) (k – 12) = 0
∴ k + 12 = 0 or k – 12 = 0
∴ k = -12 or k = 12

ii. kx (x – 2) + 6 = 0
∴ kx² – 2kx + 6 = 0
Comparing the above equation with
ax² + bx + c = 0, we get
a = k, b = -2k, c = 6
∴ ∆ = b² – 4ac
= (-2k)² – 4 × k × 6
= 4k² – 24k
∴ ∆ = 4k (k – 6)
Since, the roots are real and equal.
∴ ∆ = 0
∴ 4k (k – 6) = 0
∴ k(k – 6) = 0
∴ k = 0 or k – 6 = 0
But, if k = 0 then quadratic coefficient becomes zero.
∴ k ≠ 0
∴ k = 6

Question 1.
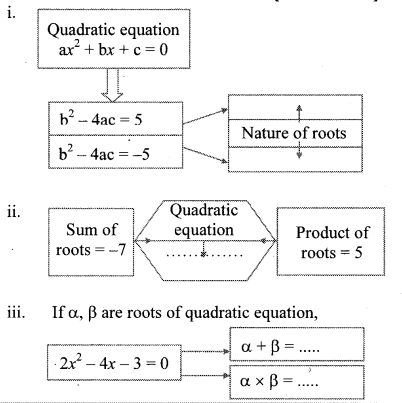
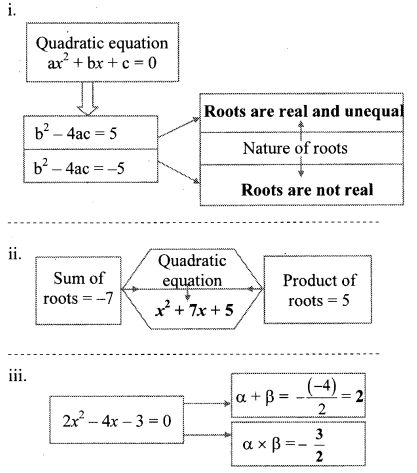
Fill in the blanks. (Textbook pg. no. 44)
Solution:

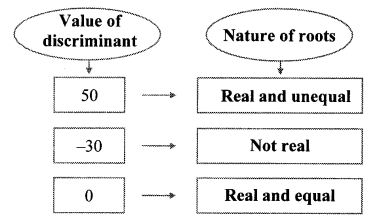
Question 2.
Determine nature of roots of the quadratic equation: x² + 2x – 9 = 0 (Textbook pg. no. 45)
Solution:

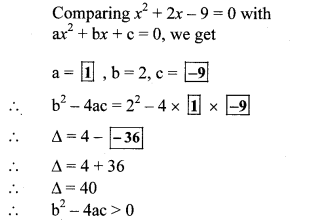
∴ The roots of the given equation are real and unequal.

Question 3.
Fill in the empty boxes properly. (Textbook pg. no. 46)
Solution:
10x² + 10x + 1 = 0
Comparing the above equation with
ax² + bx + c = 0, we get
a = 10, b = 10, c = 1

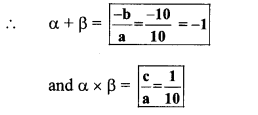
Question 4.
Write the quadratic equation if addition of the roots is 10 and product of the roots is 9. (Textbook pg, no. 48)
Answer:

Question 5.
What will be the quadratic equation if α = 2, β = 5. (Textbook pg. no, 48)
Solution: